解答含參不等式恒成立問題的常用方法

安現偉

(山東省莘縣一中教育集團新城高級中學)

證明不等式恒成立是高考必考問題,受到了師生們的關注.這類問題一般比較復雜,不但需要學生熟練掌握不等式的性質,而且需要學生靈活運用導數、分離參數、數形結合等方法,對學生有著較高的要求,導致學生的答題效果并不理想.因此,本文詳細介紹解答含參不等式恒成立問題常用到的幾種方法,以期幫助學生掌握相關知識,提高解題效率.

1 導數法

一些不等式的證明問題通常可以轉化為函數最值問題,而導數則是解答最值問題最為常用、有效的方法.在實際解題中,可以對不等式兩側進行作差處理,構造出新的函數,如此便可將不等式問題轉化為求函數最值問題.而后通過求導,進一步確定零點的范圍,借助變形與轉化,確定含零點關系式的最值,進而結合不等式恒成立的條件確定參數的取值范圍.

點評在解答本題過程中,雖然可以確定零點的存在,但是并不能直接求出.因此,對其進行設而不求,僅確定其取值范圍以及滿足關系式后對代數式進行整體替換,從而使問題獲解.

2 分離參數法

分離參數法是解答不等式問題經常用到的方法,該方法主要用于解答那些參數及變量能夠進行分離的問題.在實際解題過程中,首先需要結合不等式的特點及性質將參數進行分離,即使不等式的一側僅為參數,在此基礎上,將有變量的一側視為一個新的函數,通過求導等方法確定函數的單調性,并求出其在定義域內的最值,最后將問題進行轉化,建立起新的不等式,如將f(x)≤a恒成立轉化為fmax(x)≤a,將f(x)≥a恒成立轉化為fmin(x)≥a,進而使問題獲解.

例2已知函數f(x)＝－xlnx＋a(x＋1),若f(x)≤2a在[2,＋∞)上恒成立,求實數a的取值范圍.

則函數g(x)在[2,＋∞)上單調遞增,即得

所以a的取值范圍為(－∞,2ln2].

點評解答本題時,通過移項、變形,將a進行分離,得到a≤g(x),而后對g(x)進行求導確定其單調性,最后求出gmin(x),如此便可得到a的取值范圍.

3 數形結合法

當不等式兩側的式子明顯是兩個函數,或是可以轉化為兩個函數時,便可以借助數形結合法進行解答.在實際解題中,首先需要對不等式進行變形、轉化,將不等式兩側化為自身較為熟悉的函數表達式.然后在平面直角坐標系中準確畫出相應的圖像,這是至關重要的一步,若這一步出現問題,可能會直接導致結果錯誤.因此學生需要仔細作圖并進行檢查,最后結合圖像的位置關系、圖像的性質等建立不等式,從而使問題獲解.

例3已知不等式(x－1)2＜logax對任意x∈(1,2)恒成立,求a的取值范圍.

解析設y1＝(x－1)2,y2＝logax,當0＜a＜1時,不等式顯然不成立.

當a＞1時,在平面直角坐標系中畫出函數的圖像,如圖1所示.

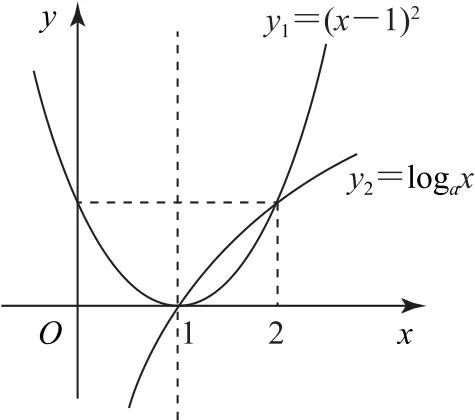
圖1

由圖1可知,當x∈(1,2)時,y1＝(x－1)2的圖像始終在y2＝logax圖像的下方,即當x∈(1,2)時,y1＜y2,此時

即loga2≥1,故a的取值范圍為(1,2].

點評本題中的不等式左、右兩邊為常見的函數,因此,只要準確地畫出相應的圖像,而后結合圖像便可以容易解答問題.在畫圖過程中,需要注意圖像的準確性和規范性.

4 同構法

對于一些既有指數函數又有對數函數的不等問題,常常可以運用同構法進行解題.對這類不等式進行整理、變形后,將其轉化為不等式兩側具有相同形式的結構,如將F(x)≥0 等價變形為f(g(x))≥f(h(x)),利用這個結構式構造對應函數f(x),進而利用f(x)的單調性、奇偶性等性質進行解題.常見的同構形式有

例4若ex－a≥lnx＋a對一切正數x恒成立,則實數a的取值范圍為( ).

解析因為ex－a≥lnx＋a,所以配湊得ex－a＋xa≥x＋lnx＝elnx＋lnx.

令函數f(x)＝ex＋x,易得f(x)在R 上為增函數,由

可知f(x－a)≥f(lnx),則有x－a≥lnx,即

設函數g(x)＝x－lnx(x＞0),求導可得

由g′(x)＝0,可得x＝1,故函數g(x)在(0,1)上單調遞減,在(1,＋∞)上單調遞增,

所以a≤gmin(x)＝1,故選B.

點評在解答本題時,通過合理配湊,同構函數f(x)＝ex＋x,而后結合其單調性將原問題轉化為對應的不等式,再進行分離參數處理,進一步可以得到函數的最小值,最后結合不等式確定參數的取值范圍,難點則是進行合理的配湊.

本文總結了解答含參不等式恒成立問題常用的四種方法:導數法、分離參數法、數形結合法及同構法.在實際解題時,學生需要結合題目進行合理的選擇,從而達到快速解題的效果.因此,在日常學習中,學生應當積極訓練,熟練掌握各種方法.

(完)