基于CEEMD能量熵與極限學習機的滾動軸承故障診斷方法

毛美姣,肖文強,陳小告,王建濤,王立超

(1.湘潭大學 機械工程與力學學院, 湖南 湘潭 411105;2.湘潭大學 復雜軌跡加工工藝及裝備教育部工程研究中心, 湖南 湘潭 411105;3.中國鐵道科學研究院機車車輛研究所, 北京 100081)

0 引言

在現代化大生產的背景下,滾動軸承是旋轉機器中不可或缺的機械元件,同時,它也是最易損壞的零件之一[1-4]。軸承一旦出現故障,輕則會對機械的性能產生一定程度的影響,重則會導致嚴重的機械事故,從而產生重大經濟損失甚至危及到人身安全[5-6]。研究表明,滾動軸承故障占機械設備總故障的45%～55%[7],嚴重影響機械的運行效率,因此,研究滾動軸承的早期故障診斷方法對提高機械運行的安全性和提前預知故障規避風險有重大意義[8]。由于環境噪聲的影響,加上滾動軸承的損傷情形比較多,導致反映軸承狀況的能量比較微弱,并且傳感器采集的振動加速度信號本身具有周期性、非平穩性、非線性,這些特征都增加了滾動軸承的故障診斷的難度[9]。

出于上述問題,從滾動軸承振動信號中分離出能夠體現其運行狀況信息的特征正成為軸承故障診斷領域的研究熱點[10-11]。經驗模態分解(EMD)適合處理非平穩、非線性信號,能把信號按頻率由高到低一步一步分解成多個線性本征模態函數的組合,然而,信號的非線性會導致部分高頻信號分解不完整,未分離出來的部分被保留到其他頻率中,當在其他頻段再次分解時則會造成模態混疊的現象。

CEEMD是在EMD的基礎上進行了一些改進,使其不僅非常適合處理非平穩、非線性信號,而且能有效抑制EMD方法產生的模態混淆,相比集成經驗模態分解(EEMD),其運算時間有所縮短[12]。經過CEEMD處理后,信號被分解成一定數量的平穩的本征模態函數(IMF),IMF分量從高頻到低頻排布[13]。滾動軸承不同部位出現故障時,由其分解出的IMF分量所包含的能量值也會相應發生改變,Yu等[14]于2006年提出能量熵的概念,用以表征機械運行狀態,并根據不同頻段能量分布的差異來診斷滾動軸承故障信息。本文中通過CEEMD對原始振動信號進行分解,得到蘊含著重要故障信息的重組信號,提取其能量作為特征,構成特征向量矩陣,并將其輸入極限學習機中,對軸承的故障特征進行學習來識別軸承的故障狀態,并與以往多采用的一些故障診斷方法進行了對比。實驗結果表明:該方法能夠有效應用于滾動軸承的故障診斷,對診斷滾動軸承的振動特征信號具有一定優勢。

1 基本理論

1.1 CEEMD方法

CEEMD是在EMD和EEMD基礎上改進而來,該方法對信號的處理過程為[12]:

用2種不同的方式為原始信號添加噪聲信號,得到兩新信號

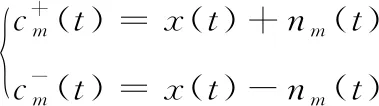
(1)

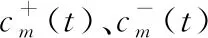
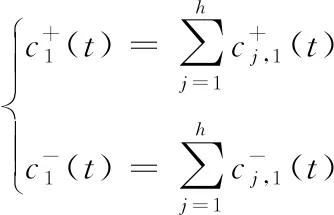
(2)

將包含加性和減性噪聲的信號分解后的IMF分量集合獲取的IMF為:

(3)

滾動軸承提取的振動信號x(t)可表示為各IMF分量與余量r(t)之和:

(4)

1.2 極限學習機

極限學習機(extreme learning machine,ELM)本質是一種單隱層前向神經網絡(single-hidden layer feedforward network,SLFN)。經典的SLFN結構包括輸入層、隱藏層以及輸出層3部分。與傳統的訓練算法不同,ELM第一步對輸入層的權值及偏置進行任意賦值,第二步通過求Moore-Penrose廣義逆矩陣的方式求解得出隱層到輸出層的權值。

從輸入層到輸出層的隱層結點,其數目的確定需要根據具體問題來分析。網絡中還包含一些待定參數:層中結點數、層偏置和層到層的權值,其數值由網絡隨機生成。生成的w、b和xn一同輸入到激活函數中,求得隱層輸出。其過程如圖1所示。

圖1 ELM示意圖

ELM的輸出可以由式得到

Y=[y1y2…yQ]m×Q

(5)

(6)

式中:n為特征的數量;Q為訓練樣本的數量;m為類的數量;l為隱藏神經元的數量;xj為輸入jth樣本;β為輸出權重;g(x)為激活函數;w為輸入層與隱藏層之間的輸入權重;b為偏置,它們都是隨機獲得的。

ELM算法較傳統的基于梯度的算法有諸多優勢,其優勢主要就在于w、b的隨機獲取,這就使其在效率方面較優于傳統的神經網絡。在求出隱層輸出之后,可以得到目標函數為:

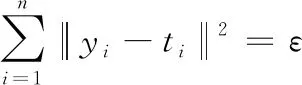
(7)

式中:ti為期望輸出值;yi為實際輸出值。通過訓練獲取使目標函數最小的參數β,這時對應的值即是最優解。

2 CEEMD能量熵與ELM相結合的滾動軸承故障診斷方法

2.1 基于CEEMD能量熵的特征向量的提取

當滾動軸承的不同部位出現故障時,在采集到的振動信號中其頻率分布也會相應地發生改變,同時,故障振動信號的能量分布也會隨之變化。因此,可以對滾動軸承的振動信號進行CEEMD分解后,計算各個IMF分量的能量熵,作為判斷滾動軸承是否出現故障的特征向量。

任意選取一組正常狀態、內圈故障、滾動體故障和外圈故障4種滾動軸承振動加速度信號進行分析。通過對滾動軸承振動加速度信號x(t)進行CEEMD分解可以得到多個IMF分量,如圖2所示。

然后按式(8)和式(9)分別計算出各個IMF分量的能量Ei(i= 1,…,n)及能量熵值HEN[17],如表1所示。

表1 熵值表

(8)

(9)

從表1中可以看出在正常狀態下,滾動軸承的CEEMD能量熵值大于其他3種情況,原因在于當滾動軸承處于正常狀態,振動信號的能量分布相對比較平均,具有很明顯的不確定性。當出現內圈、滾動體或外圈故障后,在相應的頻帶內便會出現對應的共振頻率,進而能量就會集中在該頻帶,使得能量分布的不確定性減少,導致熵值減小。因為內圈、滾動體、外圈3個部件離軸的距離為:內圈最近,滾動體其次,外圈最遠。當3個部位出現故障時,故障點對信號產生的干擾與軸的振動信號發生共振解調,從而對3種故障狀態下的振動加速度信號的穩定性產生不同程度的影響,隨著距離的增大,對穩定性的影響隨之減弱,體現在能量熵值上表現為內圈故障>滾動體故障>外圈故障。

通過以上分析可知,滾動軸承的工作狀態和故障類型不同,其CEEMD能量熵也會有顯著差異,因此可以根據CEEMD能量熵值來判斷滾動軸承的工作狀況以及故障類型。

2.2 CEEMD能量熵與ELM相結合的滾動軸承故障診斷流程

選取各個IMF的能量特征作為極限學習機的特征向量,送入極限學習機進行故障診斷,其診斷流程如圖3所示。

圖3 故障診斷流程

其具體步驟如下:

1) 在滾動軸承正常、內圈故障、滾動體故障和外圈故障狀態下,通過加速度傳感器按照固定采樣頻率fs各自進行采樣。

2) 對每種狀態下的各個振動信號進行CEEMD分解,得到一定數量的IMF分量,對于不同的振動信號,其IMF分量的數目并不相同,選取前m個蘊含重要故障信息的IMF分量當作研究對象。

3) 由式(7)計算前m個IMF的能量。

4) 構建能量特征向量:

T=[E1,E2,…,Em]

5) 因能量熵值較大,為便于對其分析和處理,對T進行歸一化得到T′。

T′=[E1/E,E2/E,…,Em/E]

6) 將特征向量T′作為ELM極限學習機的輸入,以極限學習機的輸出來確定滾動軸承的工作狀態以及故障類型。

3 滾動軸承故障診斷實例

3.1 數據來源

為了驗證所提方法的可行性,以下對其進行實例分析。采用的數據來自于美國凱斯西儲大學(CWRU)實驗室的公開數據[18],試驗臺如圖4所示。試驗采用2馬力的電機進行驅動,在電機驅動軸上裝有扭矩傳感器以及編碼器,通過測功機和電子控制系統將扭矩施加到軸上。在驅動端和風扇端安裝有SKF深溝球軸承,通過電火花加工技術在軸承不同部位設置故障,來模擬滾動軸承的不同運行狀態。

圖4 凱斯西儲大學軸承試驗臺

3.2 實例分析設計

設計的實驗方案如下:實驗軸承選擇驅動端軸承,選取0.007 in、0.014 in、0.021 in三種故障直徑將故障程度劃分為輕度、中度和重度,采樣頻率為12 kHz,電機轉速1 797 r/min,10種狀態數據樣本集共400個,每種運行狀態有40 個樣本集,運行狀態用數據編號表示,詳情見表2。每個樣本集包含2 048個原始數據點,每種運行狀態前30個樣本集作為訓練集,后10個樣本集作為測試集,并將極限學習機的分類結果與支持向量機(SVM)、k近鄰算法(KNN)、隨機森林(RF)、樸素貝葉斯(NB)、決策樹(DT)等進行對比。

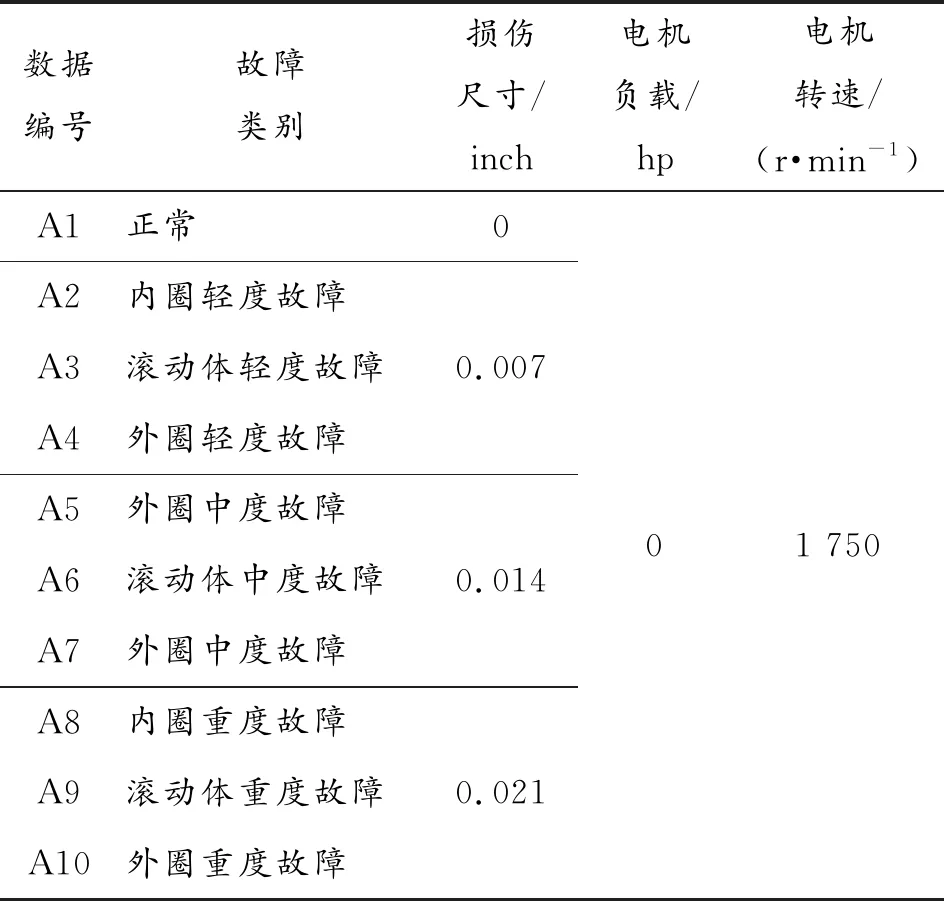
表2 振動信號數據

3.3 CEEMD能量熵特征提取

對正常、內圈故障、滾動體故障和外圈故障4種狀態下的振動信號各自采樣,分別得到40組數據。在4類數據中將前30組數據作為訓練樣本數據,將其余的10組數據作為測試樣本。第一步采用CEEMD方法對訓練數據進行處理,因為CEEMD方法具有主成分分析的效果,主要的故障信息集中在首要幾個IMF分量中(試驗得到的滾動軸承振動信號是非平穩信號而且幅值變動很大,其CEEMD分解次數均大于6)。對4種狀態信號的前6個IMF分量分別計算出能量熵,然后對其進行歸一化操作,構成特征向量矩陣。表2中只列出了滾動軸承不同工作狀態下首個取樣信號的特征向量(限于文章篇幅,特征向量僅列出一部分,且每個特征值的有效數字取3位)。表3滾動軸承不同工作狀態下的前6個分量的特征向量。

表3 特征向量表

單純地觀察表3,很難發現這些特征向量與滾動軸承各種狀態的聯系,為進一步體現出這些特征向量在表征滾動軸承運動狀態方面的效果,特將根據表2中特征向量創建的特征矩陣作為輸入,對其進行聚類可視化分析。聚類方法采用Tsne(T分布隨機鄰接嵌入)[19],聚類后所得結果如圖5所示。

圖5 Tsne狀態聚類圖

由圖5可以明顯看出,滾動軸承10種狀態類間距離較遠,除了狀態A6,其余九種狀態類內距離緊湊,分類效果較好。這說明經過CEEMD分解后,滾動軸承4種運動狀態的內在特征得到了很好地體現,將表2中的特征向量作為特征矩陣輸入極限學習機進行識別,具備了一定的可行性。

3.4 極限學習機故障識別

將每種狀態所提取特征向量的前30組輸入到極限學習機分類器中進行訓練,剩余10組輸入已經訓練好的極限學習機進行故障識別,其結果如圖6所示。

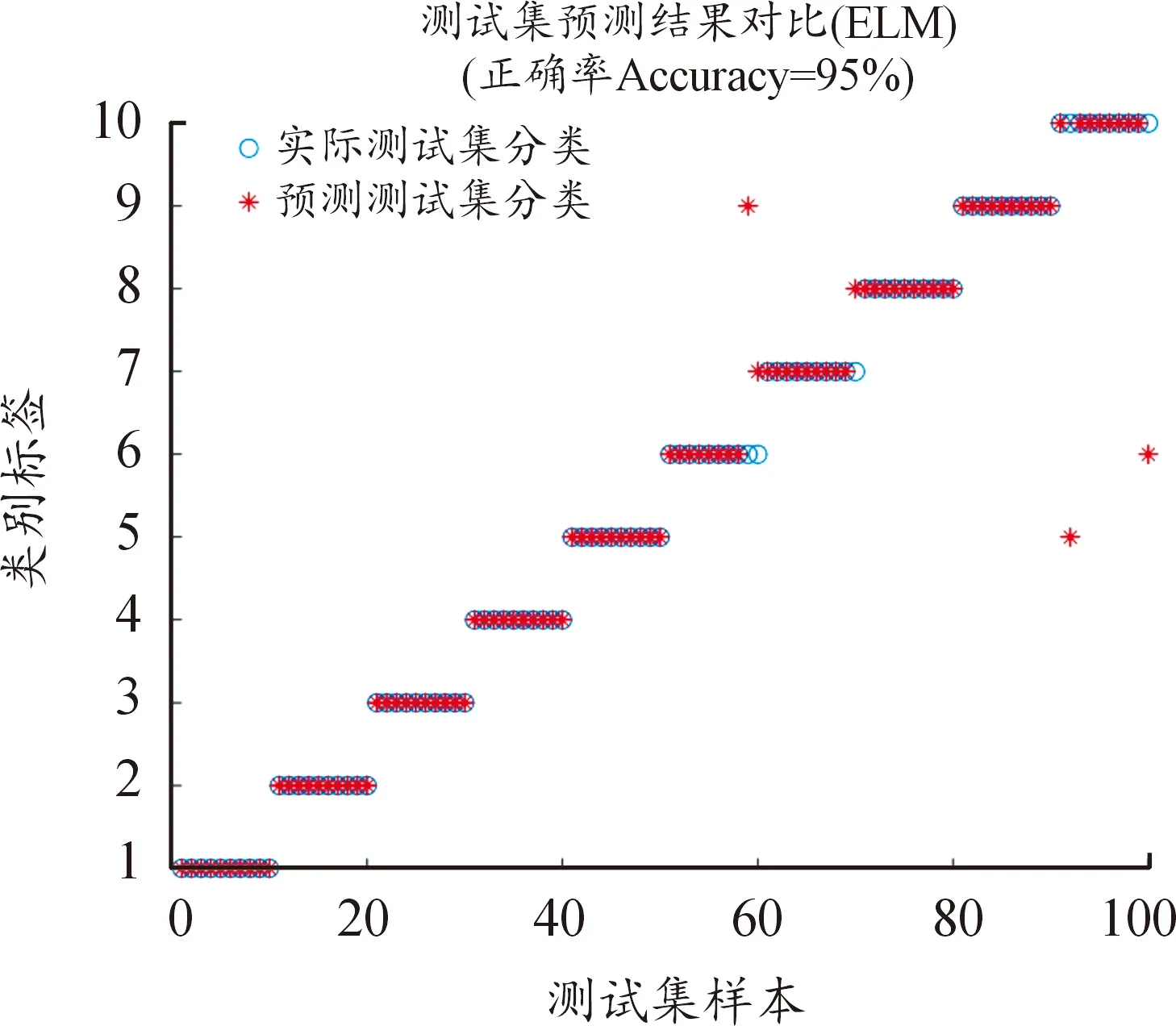
圖6 ELM測試結果

通過“1”、“2”、“3”、等10個標簽分別代表滾動軸承的十種工作狀態,可以看出經ELM識別后的結果準確率達到了95%,為進一步體現ELM的優勢,將該方法與一些機器學習算法如多分類支持向量機(MSVM)、k近鄰(KNN)、隨機森林(RF)、樸素貝葉斯(NB)、決策樹(DT)進行對比,采用交叉驗證(Cross Validation)的方式,把6種方法分別運行5次,然后求他們的平均準確率以及平均運行時間,將它們的對比結果列于表3所示。

從表4可以看出,極限學習機ELM和多分類支持向量機MSVM的準確率都比較高(分別為95%和94.25%),其次是樸素貝葉斯NB(92.75%)、K近鄰KNN(92%)、隨機森林RF(91.75%),決策樹 DT的準確率最低(88.75%)。從運行時間來,決策樹 DT的運行時間最短(0.612 6 s),其次為隨機森林RF(0.892 4 s)、樸素貝葉斯NB(1.783 3 s)、K近鄰(2.164 7 s),極限學習機ELM(2.829 7 s),多分類支持向量機MSVM(3.646 2 s)。優先考慮準確性,再綜合考慮運行時間,采用極限學習機ELM方法能獲得較高的準確性和較少的運行時間,該方法具有一定的優越性。

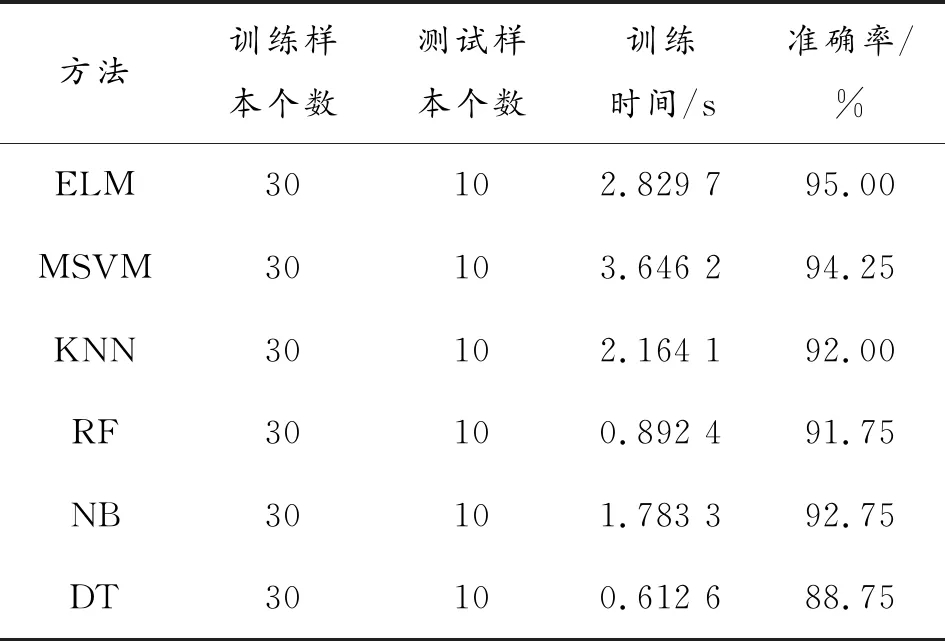
表4 測試結果對比

4 結論

1) 針對滾動軸承振動信號的非線性、非平穩特點,采用CEEMD方法對滾動軸承振動信號進行模態分解,抑制了采用EMD方法分解產生的模態混疊現象,得到IMF分量。

2) 在不同故障狀態下,采集到的軸承振動信號的頻率分布和能量分布不同,其對應的能量熵有明顯差異。在本文中,計算了各IMF分量的能量熵,將不同IMF分量的能量熵構成特征向量,用于識別滾動軸承的故障狀態。

3) 將提取到的特征向量信息輸入ELM中進行故障狀態診斷,發現ELM的準確率為95%,運行時間為最高,運行時間2.829 7 s,能很好地用于滾動軸承故障狀態的識別,具有一定的實際應用價值。