從一道聯考試題談米勒定理及其簡單應用

陳藝平

(福建省龍海第一中學,福建 漳州 363100)

米勒問題涉及三角形、直線、圓、橢圓、雙曲線等眾多知識點,經常與角度的最值問題結合考查.借助米勒定理可以迅速求解此類角度的最值問題.

1 試題呈現

題1 (華南師大附中,廣東省實驗中學,廣雅中學,深圳中學2022屆高三四校聯考第7題)在足球比賽中,球員在雙方球門前的不同的位置起腳射門對球門的威脅是不同的,出球點對球門的張角越大,射門的命中率就越高.如圖1為室內5人制足球場示意圖,設球場(矩形)長BC大約為40米,寬AB大約為20米,球門長PQ大約為4米.在某場比賽中有一位球員欲在邊線BC上某點M處射門(假設球貼地直線運行),為使得張角∠PMQ最大,則BM大約為( )(精確到米).

圖1 2022屆高三四校聯考第7題圖

A.8 B.9 C.10 D.11

2 試題分析

本題以5人制足球場為背景,求足球運動員最佳射門位置.顯然這是一道現實生活中的問題,體現了數學來源于現實并用于解決實踐問題的理念,突出了對數學建模素養的考查.試題入手寬,解法多,但是不同的解法繁簡程度不一,要求考生擇優選擇最佳路徑解決問題,突出了對數學運算素養的考查.

3 試題解析

思路1 從解析幾何的角度入手.如圖1所示,要使得張角∠PMQ最大,即tan∠PMQ最大.從函數的觀點來看,要解決最值問題,必須引入變量,即將tan∠PMQ表示成某個變量的函數,再借助函數求最值的方法解決問題.觀察圖1可知,∠PMQ=∠BMQ-∠BMP,所以可以將tan∠PMQ轉化成tan(∠BMQ-∠BMP).進一步借助兩角差的正切公式展開并引入變量解決問題.

解法1 設BM=x,x∈(0,40],

tan∠PMQ=tan(∠BMQ-∠BMP)

當且僅當x2=96,即x≈10時,tan∠PMQ取得最大值.

此時張角∠PMQ最大,所以當BM大約為10米時,張角∠PMQ最大.

思路2 思路1雖然解法自然,但是計算量大,同時也沒有看到試題背后隱含的本質.本題要尋找最佳射門位置,實則是著名的米勒問題[1].米勒是德國的一名數學家,他于1471年提出一個有趣的問題:在地球表面的什么位置,一根垂直的懸桿呈現最長?即在什么位置,視角最大?這個問題被稱為最大視角問題,又稱之為“米勒問題”.其數學表述如下:

已知點A,B是∠MON的邊ON上的兩個定點,點C是邊OM上的動點,則當點C在何處時,∠ACB最大?

可以證明如下結論:

已知點A,B是∠MON的邊ON上的兩個定點,點C是邊OM上的動點,則當且僅當△ABC的外圓與邊OM相切于點C時,∠ACB最大.

該結論簡稱為米勒定理.主要有以下三種模型.

模型1 如圖2所示,設直線a//b,直線a上有兩個定點M,N.在直線b上取一個動點P,則當點P位于過點M,N的圓與直線b相切的切點時,∠MPN最大,此時PM=PN.

圖2 模型1圖 圖3 模型2圖 圖4 模型3圖

模型2 如圖3所示,設直線a和b相交于點O,直線a上有兩個定點M,N.在直線b上取一個動點P,則當點P位于過點M,N的圓與直線b相切的切點時,∠MPN最大,此時OP2=OM·ON.

模型3 如圖4所示,設直線a與圓O1相切于點Q,直線a上有兩個定點M,N.動點P在圓O1上運動,則當點P位于過點M,N的圓O2與圓O1相切的切點時,∠MPN最大.

運用該定理可以解決數學上一些與最大角有關的問題.因此對于本題,還可以有如下解法.

顯然思路2比思路1在思維上更勝一籌,在計算上更加簡捷,體現了多思少算的良好數學品質.這也體現了命題者命制本道試題的初衷——對數學建模思想的考查。

4 拓展應用

圖5 2022年上海交大強基試題圖

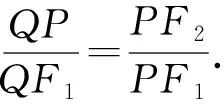
由于QP2=QF2·QF1=45,

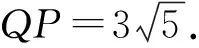
例2(2022年9月清華大學中學生標準學術能力診斷性測試)在平面直角坐標系中,A(0,1),B(0,2),若動點C在直線y=x上,圓M過A,B,C三點,則圓M的面積最小值為____.

解析如圖6所示,當圓M與直線y=x相切于點C時, 圓M的面積最小.

圖6 例2題解析圖

由割線定理可知,OC2=OA·OB=2.

在△BOC中由余弦定理可得BC2=2.

則BC2+OC2=OB2.

所以BC⊥OC.

故BC為圓M的直徑.

解析由已知可得b=2.

作直線l∥AC,當過A,C兩點的圓與直線l相切于點B時,∠ABC最大.結合已知條件易知此時△ABC為正三角形[2].

例4 已知點P為拋物線y2=4x上一動點,A(1,0),B(3,0),則∠APB的最大值為____.

解析根據米勒定理,當點P為過A,B的圓與y2=4x相切的切點時,∠APB取最大值.

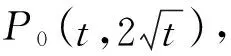
顯然P0A⊥AB,

所以△P0AB為等腰直角三角形.

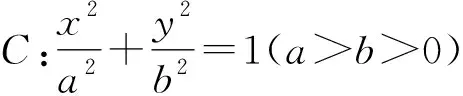
圖7 例5題解析圖

由切線定理有AP2=AF1·AF2.故AP=b.

此時P(-a,b),F1(-c,0),F2(c,0).

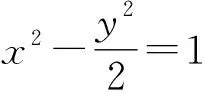
圖8 例6題解析圖

由于∠BPF1=∠BF2P(弦切角等于所夾弧對應的圓周角),得△BPF1∽△BF2P.

例7 已知點A(-1,0),B(3,0),點P為圓O:x2+y2=45上一個動點,則sin∠APB的最大值為____.

解析如圖9所示,設△ABP的外接圓圓心為M(1,t),半徑為R.當圓M與圓O相切于點P時,∠APB最大,此時O,M,P三點共線.

圖9 例7題解析圖

結合OP=OM+MP可得

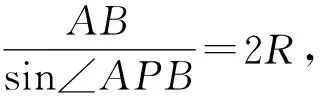
在一些現實問題中,涉及到視野的最大值問題也可以借助米勒定理解決,體現了數學建模的思想.數學建模是六大數學核心素養之一,貫穿于新教材必修一和必修二兩冊的教學內容當中.數學建模素養是教師在課堂教學中應該著力培養的素養,在平時的教學中教師可以適當介紹米勒問題,并與高中內容相結合,以此為抓手培養建模思想,提高數學思辨智慧,促進深度學習.