阿波羅尼斯圓的逆向探究及應用

浙江省寧波華茂高級中學 (315192) 崔華梅 孫續桂 戴宏照

一、提出問題

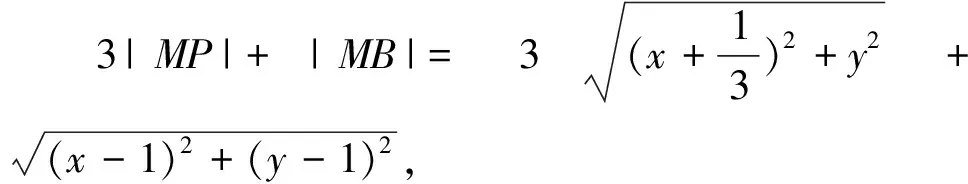
二、阿波羅尼斯圓及逆向探究

平面內到兩個定點A、B的距離之比為定值λ(λ>0,λ≠1)的動點的軌跡是圓,稱之為阿波羅尼斯圓.在解析幾何有關問題中,經常是已知圓的方程,那么,對于一個定圓,A、B兩點是確定的嗎?

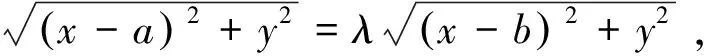
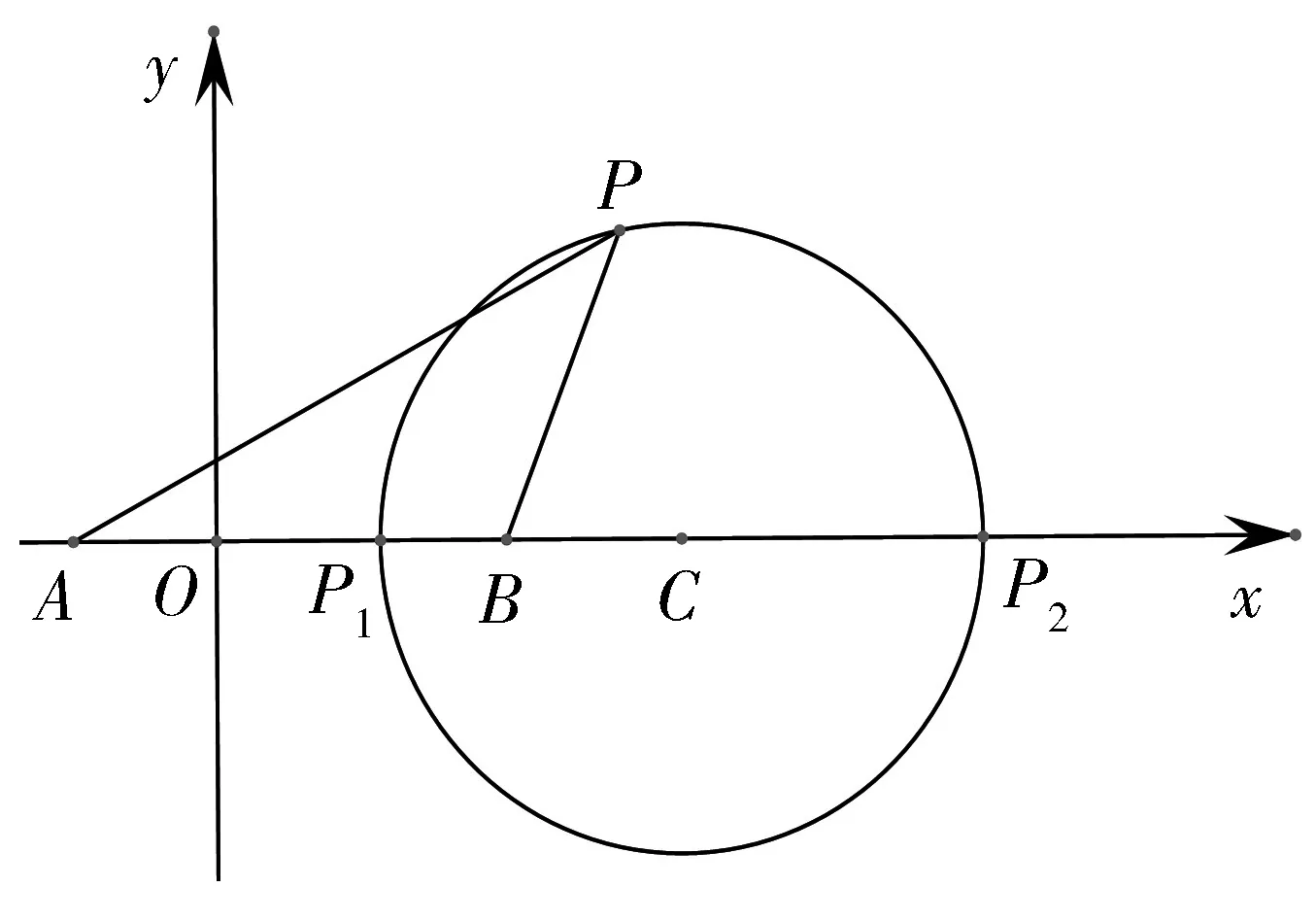
圖1

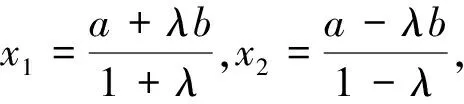
探究1 當圓C和定比λ確定時,A、B兩點唯一確定嗎?

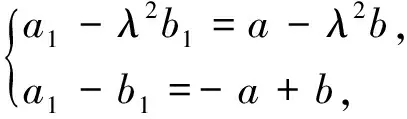
探究2 當定圓和以圓心為端點的射線確定時,比值λ和A、B兩點唯一確定嗎?

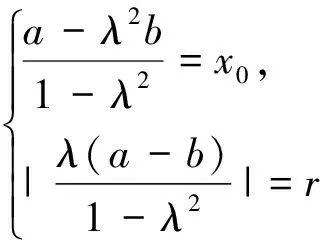
例如對于圓C:x2+y2-8x=0,當|PA|=2|PB|時,A(-4,0),B(2,0);當|PA|=3|PB|

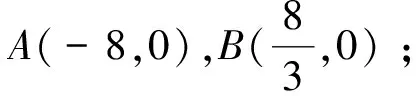
探究3 當定圓與過圓心的定直線交于P1,P2兩點時,如果比值λ確定,能否確定A、B兩點的坐標?

根據阿波羅尼斯圓的推導過程可知,x1=

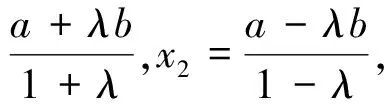
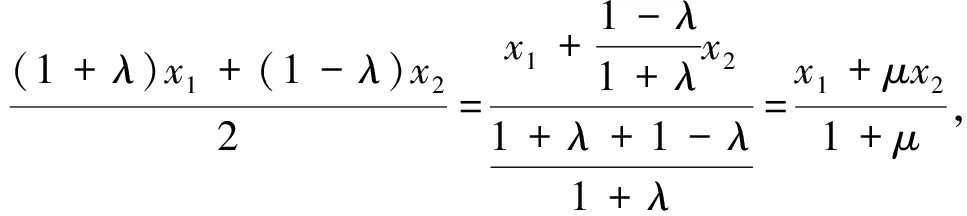
三、問題解決及推廣

通過以上探究,我們得到如下結論.

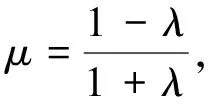
于是,就可以利用過圓心的直線與圓的兩個交點坐標求出該圓上任意一點都使|PA|=λ|PB|成立的A、B兩點的坐標.下面,我們應用此結論解決一類線段長度之和或向量模之和的最值問題.

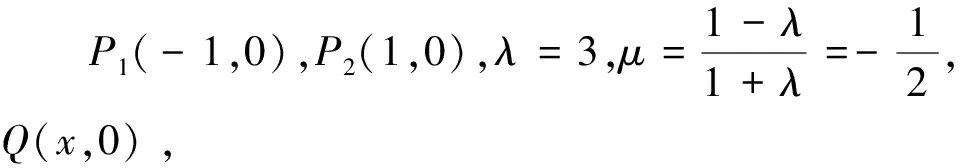
因此,求兩條線段長度之和的最值問題,如果線段前的系數不相等,就可以考慮用阿波羅尼斯圓逆向求解,先把系數轉化成相等的兩條線段長,再利用三角形三邊的不等關系,繼續轉化成過這點的一條線段長的最值問題.為了加深理解,我們再看一例:

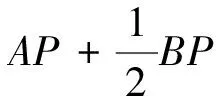
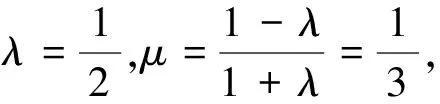
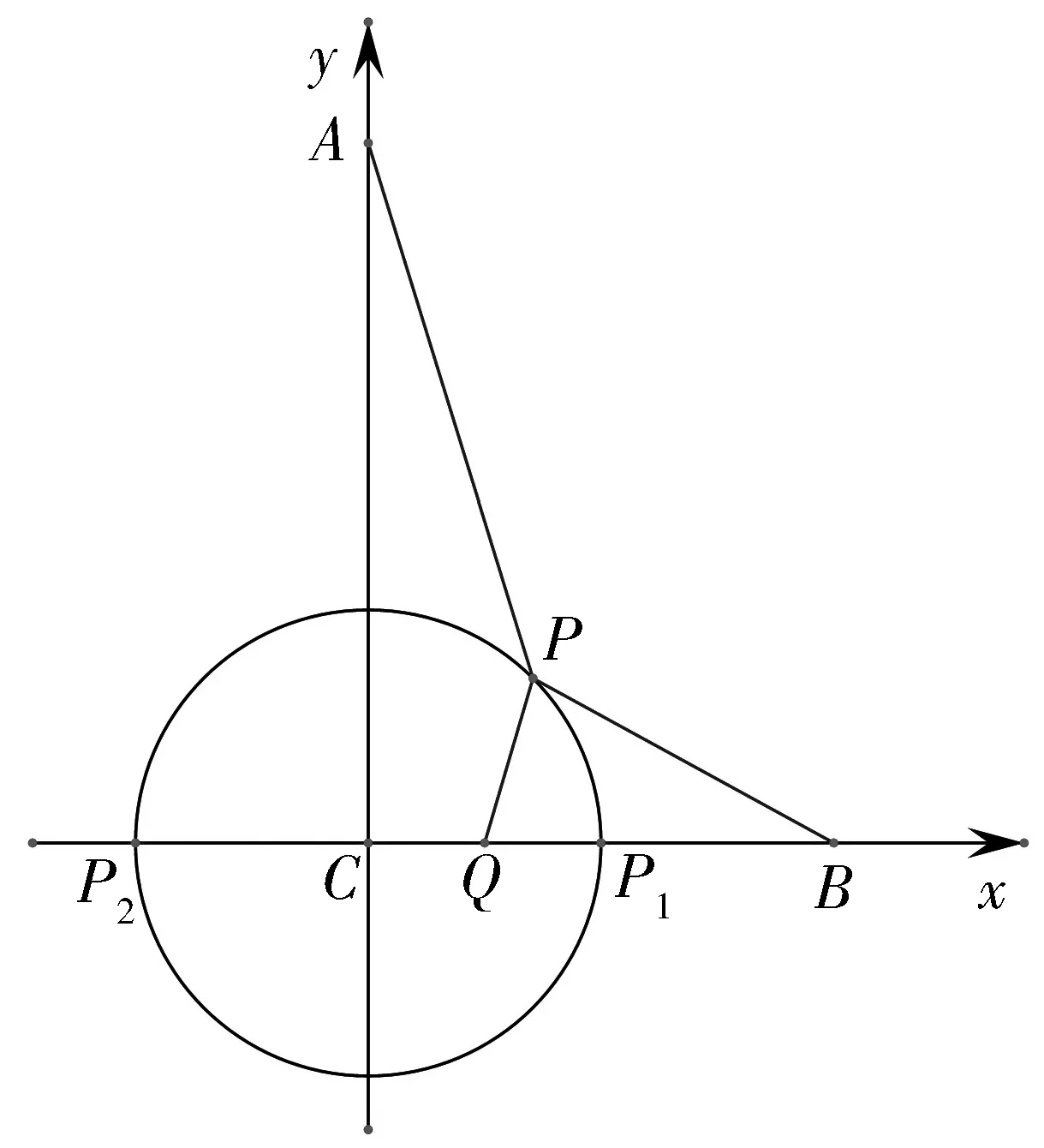
圖2

向量的模就是有向線段的長,所以這個結論也用來解決有關向量的模求和的最值問題.

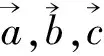
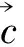
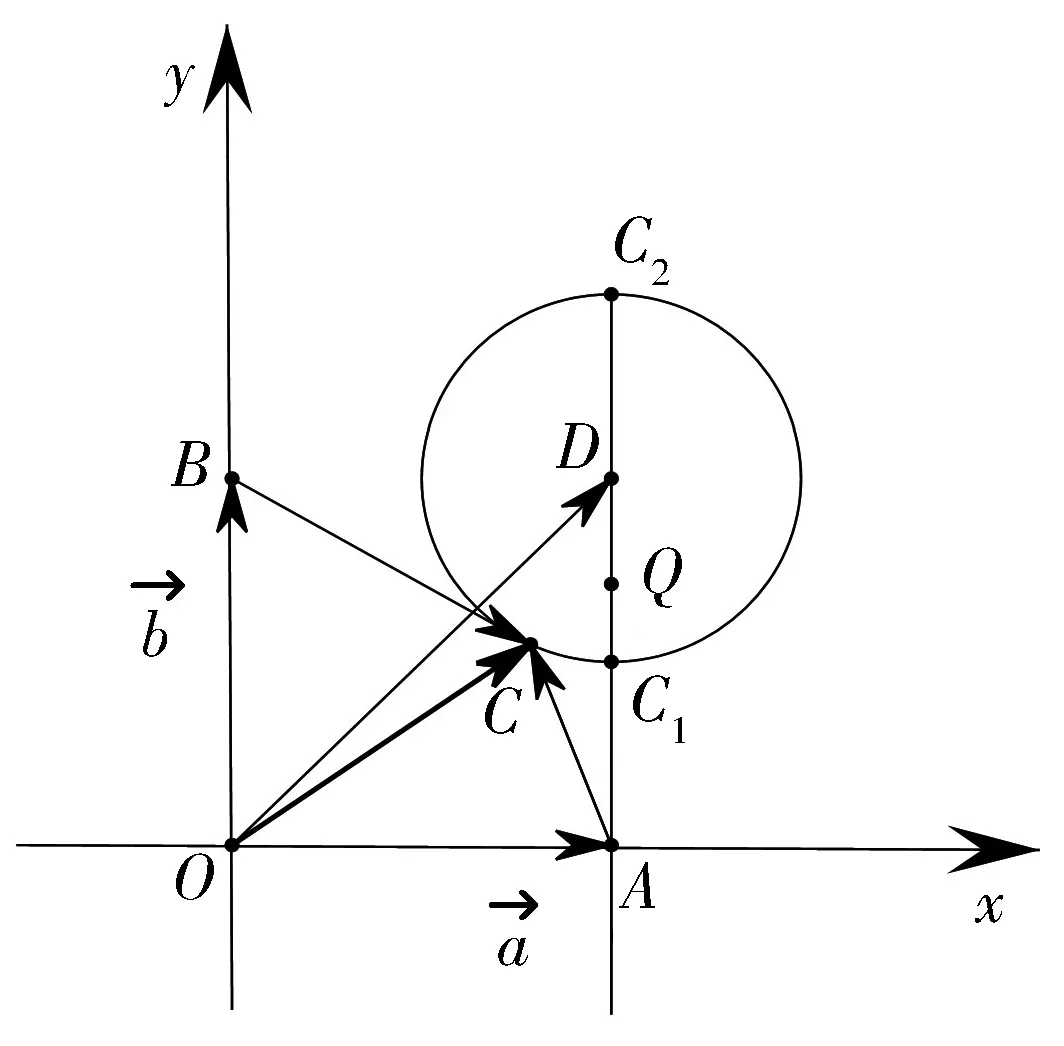
圖3

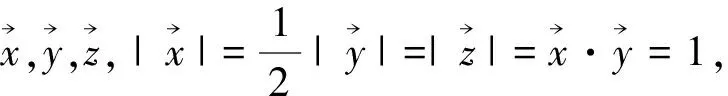
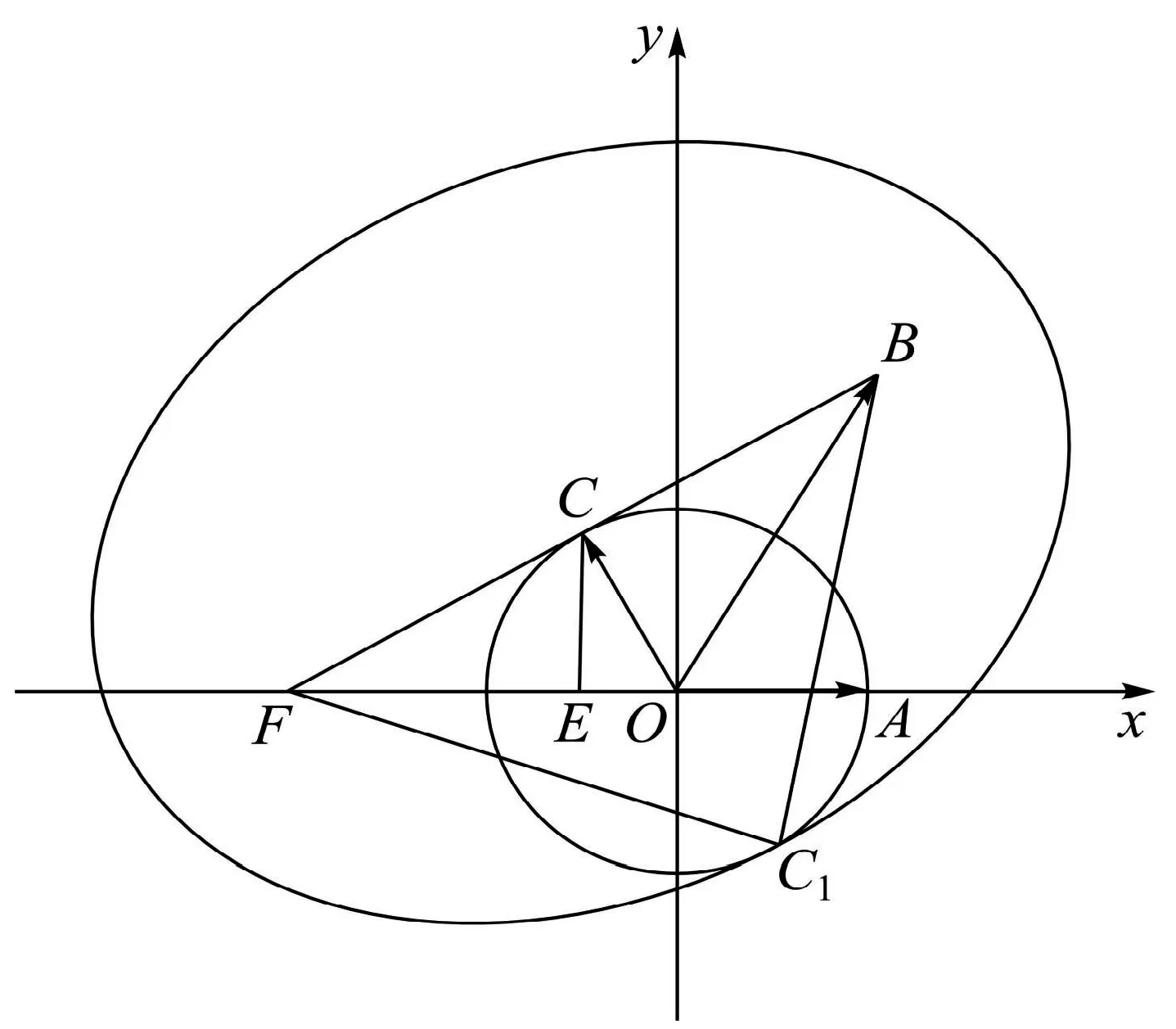
圖4

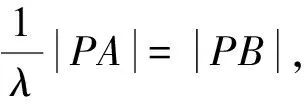
逆向思維有利于破除思維定勢,有利于認識數學問題的本質,是創新思維的一種形式;從數學核心素養上講,阿波羅尼斯圓逆向探究是建立新的數學模型,使數學問題從數學抽象,經過數學推理,易于直觀想象.