羽毛球極限揮拍速度與Fourier級數展開

董一諾 沈軒昊 聶子坤 梁熠宇*

(1.北京交通大學數學與統計學院;2.北京交通大學物理科學與工程學院 北京 100044)

1 問題提出

羽毛球是一項隔著球網，使用長柄網狀球拍擊打羽毛球的一種小型球類室內運動項目。羽毛球作為一項深受大眾喜愛的隔網對抗型體育運動，在殺球的過程中球拍接觸到球時是否能達到最大速度決定了殺球威力的強弱，也是羽毛球競技的擊球水平與觀賞性的體現［1］。為了研究羽毛球的極限速度，需要將揮拍的極限速度測量出來，目前市面上的揮拍測速裝置都需要置入對應傳感器的球拍，并且只能測出最大速度，無法測出身體其他部位的發力速度以及最后揮出的位置。該研究的意義在于更好地為羽毛球愛好者尋找出自己的不足，并提供更精確的理論訓練指導，也對羽毛球初學者如何做到正確的揮拍動作提供了指導。

2 模型建立

研究發現，揮拍時球拍的運動軌跡可以簡化為二維平面上的運動，根據人體揮拍時發力的特點：由身體、肩關節、大臂、小臂、手腕，多個部分首尾相接共同發力。這一特點與復平面下傅里葉級數展開十分相似。因此，選擇傅里葉在復數域下的展開，通過在復平面上建立首尾相接的多段向量，進行進一步計算。這里，簡化地假設肩、肘和腕關節的旋轉是獨立的，且沿同一方向。實際建模中，可能需要考慮關節間的耦合以及不同關節的旋轉軸。

復數域下的傅里葉級數展開為：

傅里葉級數可以看作是將一個周期函數分解為一系列復數向量。這些向量首尾相接，表示一個復數平面上的旋轉和縮放操作。在復數域下的傅里葉級數表示中，每個指數函數exp（inx）表示一個旋轉向量，其長度為復數系數Cn。當對所有整數n 求和時，實際上是將這些復數向量首尾相接，最終得到周期函數f（x）在每個點上的值。從幾何的角度來看，每個復數系數Cn定義了一個向量，其長度和方向分別由Cn的模和輻角決定。這些向量按照不同的頻率旋轉，形成了一個相互連接的向量鏈。將這些旋轉向量相加，可以得到原始周期函數在任何給定點的值。

根據身體各部分的數據和角速度，建立一個運動學模型。這個模型可以表示為各關節和球拍端點之間的向量方程。根據這些方程，可以計算球拍端點在揮拍過程中的速度和加速度。將角速度數據代入運動學模型，計算球拍端點在揮拍過程中的速度和加速度。

球拍端點速度=大臂長度×肩關節角速度+小臂長度×肘關節角速度+球拍長度×腕關節角速度［2］。

這個簡化的運動學模型基于以下假設：（1）肩、肘和腕關節的旋轉是獨立的；（2）所有關節沿著同一方向旋轉；（3）身體各部分的質量分布對速度計算沒有影響。

2.1 傅里葉變換

快速傅里葉變換（FFT，Fast Fourier Transform）是一種高效計算離散傅里葉變換（DFT，Discrete Fourier Transform）及其逆變換的算法。DFT 是一種將信號從時域變換到頻域的數學方法。在信號處理、圖像處理、通信等領域中，FFT算法被廣泛應用，因為它比直接計算DFT更加高效［3］。

上述公式X（k）為離散傅立葉變換（Discrete Fourier Transform，DFT）的定義。它將一個離散序列x（n）轉換為另一個離散序列X（k），其中x（n）是原始序列的時域數據，X（k）是該序列在頻域的表示。對于頻域序列中每個索引k，都計算時域序列x（n）乘以指數項exp（-2πikn/N）的和。這便得到了頻域序列X（k）的值。

使用FFT算法［4］得到的主要頻率分量圖見圖1。

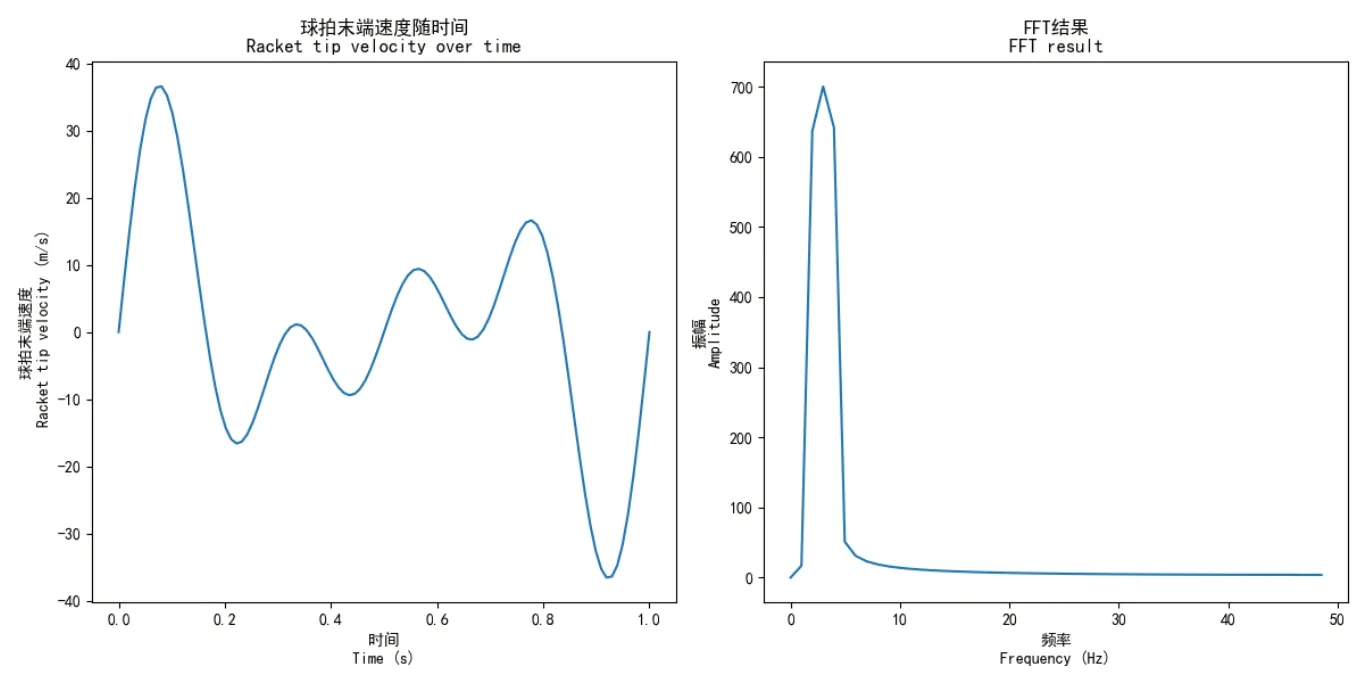
圖1 FFT頻率分量圖

球拍末端速度隨時間顯示了球拍端點速度隨時間的變化。x 軸表示時間（單位：s），y 軸表示球拍端點的速度（單位：m/s）。從圖中可以看出，速度信號呈現出周期性變化的特點。實際應用中，角速度數據將來源于傳感器或視頻分析，所以可能呈現出不同的形狀和特征。

FFT 結果顯示了速度信號的傅里葉變換結果。x軸表示頻率（單位：赫茲），y 軸表示振幅。可以看到，FFT 結果呈現出明顯的尖峰，這些尖峰對應速度信號中的主要頻率分量，揭示了不同頻率分量對整個揮拍過程的貢獻［5］。

2.2 計算理論極值

設l為力臂，w為旋轉的角速度

先以一階為例：

推廣至三階：

當t=0時，v取得最大值。

計算四階：

當t=0時，得到羽毛球的極限速度為：

3 實際分析

3.1 OpenPose的相關應用

OpenPose人體姿態識別項目是美國卡耐基梅隆大學（CMU）基于卷積神經網絡和監督學習，并以caffe 為框架開發的開源庫。可以實現人體動作、面部表情、手指運動等姿態估計，適用于單人和多人。OpenPose 提出Part Affinity Fields（PAFs），每個像素是2D 的向量，用于表征位置和方向信息。基于檢測出的關節點和關節連通區域，使用greedy inference 算法，可以將這些關節點快速對應到不同人物個體［6］。

3.2 動量守恒及能量守恒定律的相關應用

羽毛球拍擊球時可近似為彈性碰撞，由動量守恒和能量守恒定律可知：彈性碰撞前后系統的總動能不變，對兩個物體組成的系統的正碰情況滿足：

碰后m1的速度幾乎未變，仍按照原方向運動，質量小的物體以兩倍v1的速度向前運動。

3.3 羽毛球愛好者揮拍分析

收集身邊羽毛球愛好者揮拍視頻作為案例，首先進行相關測量，截取視頻中球速最快的兩幀并拼接計算轉動角速度，最終得出相關數據。

如圖2所示，測量得到球拍旋轉的角度為6°，測量可知球拍長度67 cm，身體部分參數為：大臂30 cm，小臂35 cm。已知截取視頻的放慢倍速為32 倍，幀率為30幀/秒，得到實際速度為33.67 m/s。

圖2 羽毛球愛好者小臂揮拍截圖及OpenPose模型建立

下一步進行理論速度的計算，球拍旋轉的角度為6°，間隔的時間為0.002 s，得出角速度w1=50.265 rad/s；測量得出小臂旋轉的角度為31°，計算得出角速度w2=14.840 rad/s；測量得出大臂旋轉的角度為32°，得到間隔的時間為0.147 s，計算得出角速度w3=3.803 rad/s，線性疊加得到的理論速度為：0.67×50.262+0.35×14.840+0.3×3.803=40.01（m/s）。

實際值與理論值之比為：33.67/40.01≈0.84。

3.4 專業運動員揮拍分析

根據指導教師給出的人體骨架模型，對運動員進行相關分析計算（見圖3）。

圖3 人體骨架模型相關演示

因為放慢倍數未知，可取系數a，本工作的結果是求出實際速度與理論速度的比例，故可將放慢倍數省略，通過計算得到時間為0.067 s，l為球拍長度67.5 cm，可得s=0.349 m，得到實際速度為5.24 am/s。

下一步進行理論速度的計算，球拍旋轉的角度為32°，間隔的時間為0.1 s，計算得出角速度w1=6.283 rad/s；測量得出小臂旋轉的角度為37°，得到間隔的時間為0.3 s，計算得出角速度為w2=2.153 rad/s；測量得出大臂旋轉的角度為31°，得到間隔的時間為1 s，計算得出角速度為w3=0.541 rad/s；測量得出身體旋轉的角度為31°，得到間隔的時間為5.633 s，得出角速度為w4=0.096 rad/s。線性疊加得到的理論速度為0.67×6.28+0.35×2.15+0.3×0.54+1.7×0.096=5.28（am/s）。

實際值與理論值之比為：5.24/5.28≈0.992。

4 結論與建議

通過模型建立以及對案例的具體分析，從普通人和運動員兩個部分分別分析。先將羽毛球運動分解為大臂、小臂、身體轉動和球拍四部分，逐步分析實際速度與理論速度的差別。通過分析得出：業余球員揮拍速度主要依靠最后一個關節的角速度，在缺少身體轉動的時候依舊只能達到理論值的84%。而職業球員四段發力的傳導完整，實際速度與理論速度高度一致。故對于業余球員來說，提升球技依舊需要鍛煉揮拍的集中發力，加強整體發力的協調性，這比單純的力量訓練對球速的提升更明顯。