HPM視角下弧度制教學的再思考

蔣逸卿 鄭蓉蓉 唐恒鈞

【摘 要】弧度制一直是高中數學教學中較難把握的內容。近年來，隨著HPM教學理念的廣泛傳播，HPM視角下弧度制的教學設計案例逐漸增多，但在凸顯知識發生發展和促進學生理解概念的過程中還存在一些不易處理的問題。本文提出弧度制教學中四個普遍存在的問題，評析現有HPM視角下弧度制教學設計處理這四個問題的典型方案，最后根據弧度制的歷史發展脈絡對教學內容進行整合重構，給出針對四個問題的教學設計。

【關鍵詞】HPM；弧度制；教學設計；教學反思

一、引言

HPM視角下的教學研究不斷深入，實踐表明，在課堂教學方面，數學史具有知識之諧、方法之美、探究之樂、能力之助、文化之魅、德育之效等六類教育價值［1］。弧度制一直是高中數學教學中的一個熱點和難點，基于HPM視角的弧度制教學可以從多方面突破難點，提高課堂的有效性。弧度制教學設計中目前還存在一些較難處理的問題，本文試圖梳理和評析現有HPM視角下弧度制教學設計處理這些難題的典型方案，嘗試根據弧度制歷史發展脈絡整合教學內容，并借鑒現有研究的處理思路，對弧度制教學的重構設計進行探索，以期為現有弧度制教學提供有益的參考。

二、HPM視角下弧度制教學研究現狀審視

弧度制一課的教學設計中，主要有以下四個較難處理的問題：

（1）引入環節如何自然凸顯弧度制的必要性和內在邏輯。

（2）尋找可以表示角的新的量（標準）并進行驗證時如何體現合理性與關聯性。

（3）尋求新制度（弧度制）下的“單位1”時直接就令l/r=1。

（4）得到1弧度的角的定義后直接給出了任意角定量表示|α|=l/r。

現有HPM視角下弧度制的教學設計是如何回應上述四個問題的？下面評析幾種典型的處理方案。

（一）引入環節如何自然凸顯弧度制的必要性和內在邏輯

現有教學設計對該問題的關注程度較高，也涌現出很多切實有效的策略，其中以“函數定義沖突型”和“單位制型”兩類方案最為普遍和典型。

方案1：函數定義沖突型

這類方案的引入思路一般是先讓學生回憶初中所學的銳角三角函數，舉出例子，再反思是否符合高中對應關系的函數定義，引發認知沖突，為能在原有函數體系中建立三角函數的概念而引入弧度制。

這種方式指明了學習弧度制的目的，在凸顯學習弧度制的必要性和內在邏輯上的效果顯著，學生能體會到學習弧度制是必要的、重要的，這為問題（1）的解決提供了非常不錯的思路。但還有問題值得繼續思考：是否六十進制的角度不是實數？事實上，角度與弧度一樣，都是度量平面角的量值，具有單位量，“度”或“弧度”并不影響其本身實數屬性；角度單位“度、分、秒”之間每逢60進1，但度以上并無更大的單位，因此角度數常常表示為十進制的數［2］。綜上，角度不是實數的觀點的理論依據有所欠缺。此外，由于研究的方向是用實數表示角而非統一度量單位，后續環節在數學史的融入方面可能有一定困難。基于以上緣由，這類方案近年來逐漸式微，取而代之的是從單位制出發的方案。

方案2：單位制型

這類方案從同一問題中單位的適切性、統一性的角度引出弧度制，可以分為多種度量制度式和單位不統一式兩種類型。

多種度量制度式沿用教科書的引入思想：類比物理量的不同度量制，讓學生體會一個量可以有多種單位制，不同的單位制各有優勢，單位的選擇要與問題貼合，從這個角度引出可能有其他度量角的方式（弧度制）。以物理量具有不同單位制為例的引入方式符合學生的認知，可以很好地激發學生探尋角的其他度量方式的興趣。但本質上一個量的多種單位制與弧度制的邏輯關聯不強，弧度制引入的必要性與思維指向性有所不足［3］，數學史的融入方式易停留于附加式和復制式。

單位不統一式通過設置數學情境和提出引發認知沖突的問題（比如[sinα]與[α]的關系），來明確統一角度單位與長度單位的研究目標。這一目標與驅動弧度制產生和發展的目的是一致的，因此將知識線、活動線與統一弧長、半徑度量的歷史發展線相交融，從而厘清數學本源，為學生生成積極的內在學習動機，引導學生經歷“再創造”的過程。當然這類方式也有不易處理的地方，比如情境問題“[30°]+sin[30°]等于多少？”是值得商榷的，即使用弧度制，[30°]轉換為了 π/6rad，它本身依然是量值，與數值sin[30°]仍然無法相加。

（二）新度量制度的建立如何具有脈絡而不突兀

本部分內容討論現有教學設計針對問題（2）（3）（4）的典型處理方案，這三個問題指向的是弧度制的建立過程，如何做到自然連貫、脈絡分明是值得深思的。

方案1：比值-單位-定量表示型

這類方案與教科書呈現的思路一致，即從弧長公式出發，探究弧長與半徑、角之間的關系，學生經歷猜想、驗證，認識到用[lr]度量角的合理性，接著考慮到表示方法應力求簡潔，令l/r=1給出1弧度角和弧度制的概念，再通過作特殊弧度的角的練習得到任意角的定量表示。這種做法在尋找度量標準[lr]的環節上具有較強的探究性，能讓學生經歷概念的自主建構，體會數學抽象的過程。但學生對新度量制的標準是缺少認識的，容易導致目標指向不明而陷于盲目的規律探尋中。此外，用l/r=1的簡潔性來解釋“單位1”的產生略顯生硬，說服力不夠，反映由單位角到定量表示任意角的內在邏輯還不夠清晰。

方案2：單位生成型

單位生成型以度量單位的產生和應用為主線，引導學生經歷“類比角度制—規定單位1—應用單位1度量其他角”的過程，使得數學史的融入自然透徹。學生能較好理解l/r的本質即為倍數，而不只是一個與角互相確定的量而已，于是|α|=l/r就呼之欲出了。在這種方案下，學生獲得了單位制生成的經驗，能體會規定單位1的必要性，且基于思維的可逆性，能從半徑出發得到規定單位1的方法。當然，這一方案也存在可以探究的地方，比如為何以r為1個單位去量弧長和角而不是用1厘米或1米？顯然后者會導致角與度量值無法一一對應，但不可否認這會是學生最自然的想法，在教學中不應被忽略。

縱觀上述針對四個問題的典型方案可知，HPM視角下的教學設計應高度關注弧度制本身的發展脈絡。

三、弧度制的數學發展脈絡

不管是在數學史上還是在數學教學上，角度制與弧度制之間的關系都具有重要意義，弧度制的建立離不開對角度制等分圓周之本質的借鑒，而弧度制與角度制之間的共性與差異又能加深學生對數學本質的理解。因此，本文從角度制的起源開始，根據啟蒙期、傳播期、確立期［4］三個發展階段的主要內容，梳理弧度制產生與發展的脈絡。

（一）啟蒙期

角的度量起源于對兩條相交直線分離程度的定量刻畫的需求。一般認為由古巴比倫人在等分圓周的基礎上，實現了圓弧的度量，在弧與角建立一一對應關系后得到了角的度量，將每一份圓弧所對應的圓心角定義為1度的角。

（二）傳播期

天文學家托勒密出于方便計算的考量，在古巴比倫人的基礎上對“1度”又做了兩次更細致的等分，形成了如今用“度、分、秒”度量角的單位制度——角度制。托勒密及其后的印度數學家阿耶波多在實際計算中注意到弧長與弦長應采用相同的度量單位，因此以弧長的度量單位為準，借助公式2 πr=[360°=21600′]，實現了半徑與弧長度量單位的統一。但以弧長單位為基準去實現統一，使得弧長與半徑都處于六十進制度量之下，從整體看，計算并未得到實質性簡化。

（三）確立期

直到18世紀中期，數學家歐拉逆向思考，提出以半徑為單位來度量弧長及對應的圓心角。弧度制的概念由此正式產生，其本質是用十進制的長度單位實現了弧長與半徑的統一。

綜上，天文學計算中度量單位不統一造成的運算不便是弧度制產生的動力源。從以弧長（圓心角）的度量單位為基準到以半徑為度量單位，天文學家、數學家們為統一度量制，經歷了啟蒙期、傳播期、確立期三個階段的漫長探索。

四、HPM視角下弧度制的教學重構

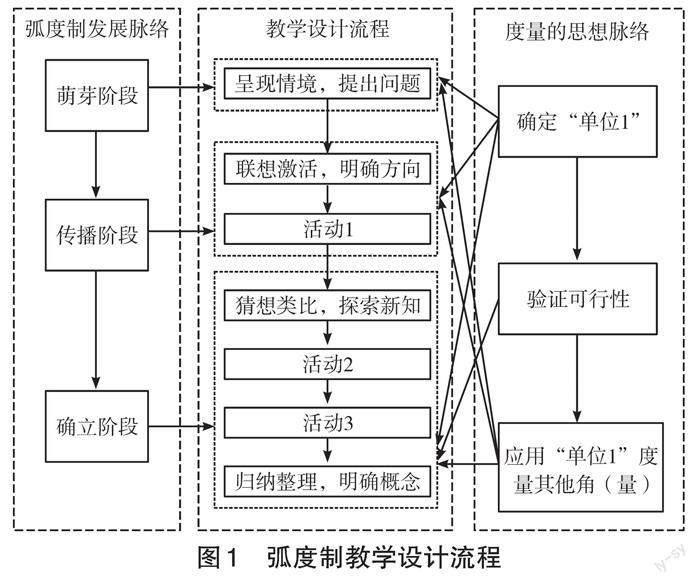
HPM視角下的弧度制教學需特別關注弧度制本身的發展脈絡，本文基于對上述史料脈絡結構的提取，以弧度制的發生發展脈絡為架構點，以符合學生認知規律為出發點，重構教學活動。以“度量”的思想為主線［5］，在不斷提取和應用的過程中使其逐漸清晰、完善，加深學生對知識本質的理解和認識。教學設計流程見圖1。

本文呈現的教學設計僅涵蓋前文提及的四個問題所對應的教學內容，即弧度制的引入到任意角的定量表示。其中“1.呈現情境，提出問題”針對問題（1）的解決，“2.聯想激活，明確方向”“3.猜想類比，探索新知”“4.歸納整理，明確概念”針對問題（2）（3）（4）的解決。

1.呈現情境，提出問題

【情境】（1）如圖2所示，自行車以20km/h的速度行駛在馬路上，其行駛時間y（h）關于路程x（km）的函數關系式是怎樣的？（2）如圖3所示，過山車沿著一段半徑為20m的半圓形軌道運行，其離地高度y（m）關于旋轉角度x的函數關系式是怎樣的？

問題1：函數y=0.05x的自變量x是什么類型的數？函數y=20sinx的自變量x是什么？

問題2：函數h（x）=0.05x+20sinx的自變量x又是什么？h（10）有意義嗎？你遇到了什么問題？

問題2-1：如何讓函數h（x）有意義？

【預設】學生發現在函數h（x）中自變量的單位不統一，即一個是長度單位一個是角度單位，為了使函數有意義，提出統一單位的想法。對于角來說，可能需要采取一種以長度單位為基礎的度量方式。

【設計意圖】根據本文第二部分“二、HPM視角下弧度制教學研究現狀審視”的評析，“單位不統一式”的引入方式在教學中具有較大的優勢。因此首先設置情境，引導學生寫出自變量使用不同單位制的兩個函數關系式，由函數的和引出一個函數中自變量單位制不同的問題，用h（10）存在意義的問題將認知沖突推向高潮，激發學生想要了解自變量為一般數值時三角函數的意義的強烈欲望，從而引出對長度單位、角度單位統一的探究，避免了前文所述的使用了弧度制也無法解決[sin30°與30°]不能相加問題的尷尬。

問題3：我們是如何度量角的大小的？

教師引導學生回憶角度制的定義，并播放視頻呈現古巴比倫人建立角度制的過程：古巴比倫人最早創立了以六十進制為基礎的角度制，即把圓周進行360等分，每1份弧長對應的圓心角定義為1度的角，記作[1°]。

教師提出，除了把圓周等分的角度制外，歷史上還有許多其他類型的度量角的方法。教師呈現歷史上法國等分圓周建立的十進制的角度制，軍事上的密位制，天文學中等分圓周形成的角度制等資料。

問題4：這些度量方法有何相同點？有何局限？

【預設】學生歸納出這些方法都把圓周進行了一定數目的等分，得到一定大小的單位角后再去量其他角的大小。教師引導學生發現等分圓周具有隨意性和偶然性，容易造成跨地區和跨領域交流的不便，因此若能建立一種與長度單位統一的度量角的方式，或許有解決這類問題的優勢。

【設計意圖】問題3通過回憶角度制以及介紹其他本質相同的量角方式，讓學生了解度量單位建立的基本路徑。問題4讓學生歸納所述度量方法的共性，體會以等分圓周為基礎的量角方式的局限，從另一個側面體會統一單位建立新度量方式的必要性。

2.聯想激活，明確方向

問題5：再次思考古巴比倫人定義1度角時的順序，你能發現什么？

【預設】教師引導學生發現古巴比倫人采用的“度”這個單位最早是刻畫圓弧的長度單位，在圓心角和圓弧之間建立起一一對應的關系后，才將它作為度量角的單位。教師可以指出，這導致數學家們進行圓的相關計算時遇到了麻煩，源于弧長的單位與半徑的單位并不統一，也就是角度單位與長度單位不統一。

問題6：歷史上數學家們為弧長和半徑度量單位的統一做了很多工作，你們認為對兩者進行統一的方向是什么？

學生提出，度量單位的統一要么都采用歷史上弧長的度量單位，要么都使用半徑的度量單位。

活動1：探究如何采用歷史上弧長的單位（即“度”）去度量半徑。

問題7：如果都使用圓心角和弧長的度量單位（度），那么半徑長是多少（度）呢？

【預設】學生討論探究。教師展示托勒密做過的工作，即借助 2πr=360[°]得到直徑為360°/π度，近似為120度，半徑就是60度，半徑和任意弧長都可以統一用弧長的單位（度）來表示了。教師指出，這同樣帶來了問題，在平面幾何的研究工作中采用得最為普遍的是長度單位，統一使用弧長單位就會使得眾多計算需要轉化單位而變得十分煩瑣。因此，學生猜想也許統一用半徑的單位來度量會更方便。

3.猜想類比，探索新知

問題8：如果都使用半徑的度量單位，如何度量圓心角和弧長呢？

問題8-1：半徑的度量單位是什么？

活動2：探究并驗證采用基本的長度單位度量圓心角大小的可行性。

問題9：直接使用半徑的度量單位刻畫圓心角是否可行？請探究驗證。

【預設】學生合作探究，繪制出同心圓后發現，有弧長公式l=nπr/180，在弧長固定時圓心角的大小與半徑大小成反比，可能導致同樣單位數的圓心角的實際大小不同。

師：這給你怎樣的啟示？

生：使用一個新的標準去度量角的大小必須遵循相應的原則，即角相同時新的量也應該相等，角不同時新的量也要不同。

【要點說明】學生最自然想到的是用1cm長的圓弧作為度量弧長的1個單位，類比角度制的定義，1cm的弧所對的圓心角也就記作1個單位角，理應能順利刻畫角的大小，即要確定一個圓心角[θ]的大小，只需計算出其所對的圓弧長s對于一個單位角所對圓弧長的倍數m，圓心角[θ]的大小就是m個單位。但學生通過探究發現這種方法不可行，教師進而引導學生進行歸納，即使用新的標準去度量角的大小必須遵循相應的原則。

教師呈現歐拉創造性想法的多媒體資料。

問題10：歷史上，數學家歐拉提出以半徑為單位來度量弧長。如果將半徑本身作為1個單位，則圓周長、半圓周長為多少個單位長度？

活動3：類比探究以半徑為單位度量圓心角的大小是否可行。

問題11：如何以半徑作為1個單位度量圓心角的大小？是否可行？

【預設】學生再次沿著度量單位建立的路徑，先確定1個單位角，即半徑長的圓弧所對的圓心角定義為1個單位角。有了前面度量的經驗，學生能得到圓心角[α]的大小就等于所對應的圓弧長l對于1個單位角的圓弧長r的倍數，即[l/r]。借助信息技術，學生探究用[l/r]表示圓心角[α]的大小的可行性，即是否滿足角相同時新的量也應該相等的原則。最后，在教師的引導下用弧長公式進行嚴謹證明。弧度制下，角定量表示的關系式呼之欲出。

4.歸納整理，明確概念

問題12：請回顧并總結活動2和活動3是怎樣一步一步完成角的度量的？

生：我們類比了古巴比倫人定義1度角的方式，先得到了一定大小的圓弧的1個單位，再定義它所對應的圓心角是1個單位的角，對可行性進行驗證后，便能以這個單位角去度量其他角的大小了。

教師呈現1弧度的角和弧度制的定義。

問題13：利用關系式[α=l/r]是否就可以表示任意的角？

問題13-1：能否嘗試作出2rad的角？-2rad的角呢？

問題13-2：回顧作角的過程，反思關系式[α=l/r]是否一直成立？若不成立應該如何調整？

【設計意圖】采用改進的“單位生成型”方案，將“度量”思想的主線與“統一弧長與半徑單位”的歷史發展線深刻融合、互相交織，學生反復經歷“確定單位1—驗證可行性—度量其他角”的過程。在類比和逆向思維的引導下，學生能主動提出1個單位的確定方法并發現任意角定量表示的雛形。此外，正視學生的想法，將以1cm、1m作為1個單位的想法主動暴露在課堂中，并以此為契機引導學生探究、歸納用新標準度量角需要遵循的原則，并結合該原則進行嚴謹的驗證，發展了學生重論據、有條理、合乎邏輯的思維品質和理性精神。

五、小結

本案例彰顯了數學史的教育價值。在已有史料基礎上，從啟蒙期、傳播期、確立期三個階段提煉出了弧度制的發展脈絡，教學流程的每個環節都基于相應的脈絡節點進行重構設計。比如第一個環節“1.呈現情境，提出問題”，在引發認知沖突，明確統一度量的目標后，學生自然需要對度量角的方式進行反思，因此從啟蒙期的角度制出發，體會度量角的基本路徑，加深對角度及角度單位本身的認識，體現了知識之諧。

本案例以傳播期、確立期兩個階段的發展脈絡為依據，設計了三個探究活動。活動1學生實際上循著托勒密、阿耶波多的思想進行統一度量的工作，活動2和活動3則沿著歐拉的思想，在探究中逐步接近弧度制的內核。在此過程中，學生深入弧度制發生發展的歷程，在探究中發現并解決問題，享受探究的樂趣，積累了“度量”的活動經驗，體現了探究之樂。從活動1至活動3，學生不斷沿著“確定單位1—驗證可行性—度量其他角”的初始路徑嘗試進行度量制的統一工作。在活動2中，學生發現采用1cm等長度單位去度量角會出現問題，并概括出使用新標準進行度量須遵循的原則。活動3中學生將該原則運用于猜想的驗證上，進一步理解“驗證可行性”這一步驟的重要性。學生在此過程中認識到直覺判斷的局限性，認識到對猜想進行嚴謹驗證的重要性，展現了德育之效。

參考文獻：

［1］陳晏蓉，汪曉勤. 數學史料的選取原則與案例分析［J］. 教育研究與評論（中學教育教學），2017（12）：37-43.

［2］王姿婷，朱一心，王安. 關于弧度制中幾點誤讀的分析［J］. 數學通報，2021（12）：23-27.

［3］商再金，翟洪亮. 展現思維過程 促進概念理解：對“弧度制”教學的思考［J］. 中學數學月刊，2023（1）：15-16，39.

［4］江灼豪，何小亞. 弧度制發展的歷史溯源［J］. 數學通報，2016（7）：14-17.

［5］劉燁燁.“弧度制”教學實錄與反思［J］. 中國數學教育（高中版），2020（6）：35-39.

（責任編輯：潘安）

【作者簡介】蔣逸卿，浙江師范大學教育學院在讀碩士研究生，主要從事數學課程與教學研究；鄭蓉蓉，浙江師范大學教育學院在讀碩士研究生，主要從事數學課程與教學研究；唐恒鈞（通訊作者），浙江師范大學教授，博士生導師，主要從事數學課程與教學研究。