基于改進(jìn)模糊聚類算法的數(shù)據(jù)信息分析與預(yù)測(cè)模型設(shè)計(jì)
高楚淮
(河北北方學(xué)院附屬第一醫(yī)院,河北 張家口 075000)
隨著藥品生產(chǎn)供應(yīng)市場(chǎng)的發(fā)展,建立安全完備的藥品研制、生產(chǎn)及流通體系勢(shì)在必行。當(dāng)前我國(guó)的醫(yī)藥市場(chǎng)主體依然呈現(xiàn)出“多、散、小”的格局,且藥品的基礎(chǔ)資料多為非結(jié)構(gòu)化數(shù)據(jù),故仍存在信息統(tǒng)計(jì)與查詢困難的問(wèn)題。而如何運(yùn)用大數(shù)據(jù)平臺(tái)進(jìn)行藥品信息的分析,并實(shí)現(xiàn)準(zhǔn)確的分類及預(yù)測(cè),對(duì)藥品流通的所有參與者而言均具有重要意義。對(duì)于監(jiān)管者,其可建立行之有效的安全風(fēng)險(xiǎn)防范體系;而對(duì)于醫(yī)療機(jī)構(gòu),則能優(yōu)化供應(yīng)鏈管理水平,進(jìn)而逐步實(shí)現(xiàn)運(yùn)行模式的優(yōu)化[1-4]。
聚類分析(Cluster Analysis)是數(shù)據(jù)挖掘領(lǐng)域的常用算法,近年來(lái)基于劃分、層次與密度分析等思路,該算法得到了進(jìn)一步的發(fā)展[5-11]。其中,模糊聚類(Fuzzy C-Means,F(xiàn)CM)算法是一種基于模糊數(shù)學(xué)理論的機(jī)器學(xué)習(xí)(Machine Learning,ML)算法。與其他聚類算法不同的是,其引入了隸屬度函數(shù),增添了樣本類別的非定性描述,使得物體與客觀世界建立了更為契合的映射關(guān)系。此外,該方法無(wú)需訓(xùn)練樣本,是一種無(wú)監(jiān)督的聚類方法,并可自動(dòng)提取藥品信息中的特征,進(jìn)而實(shí)現(xiàn)樣本的自主分類。文中在對(duì)常用的、基于目標(biāo)函數(shù)的模糊聚類分析算法進(jìn)行討論的基礎(chǔ)上,結(jié)合醫(yī)藥數(shù)據(jù)信息分析的應(yīng)用場(chǎng)景對(duì)該算法加以改進(jìn)。仿真結(jié)果表明,改進(jìn)后的算法在對(duì)藥品數(shù)據(jù)進(jìn)行聚類預(yù)測(cè)時(shí),關(guān)鍵性指標(biāo)有了顯著改善。
1 理論基礎(chǔ)
1.1 傳統(tǒng)模糊聚類算法
基于目標(biāo)函數(shù)的模糊C 均值聚類(FCM)算法是模糊集理論中常用的數(shù)據(jù)分析方法[12-14],其結(jié)構(gòu)簡(jiǎn)單且計(jì)算復(fù)雜度較低,并可對(duì)樣本數(shù)據(jù)進(jìn)行自動(dòng)分類。FCM 算法的基本流程如圖1 所示。
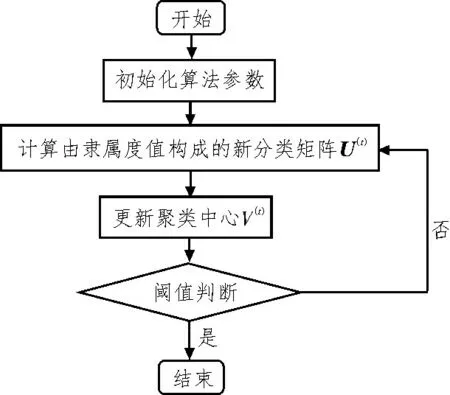
圖1 傳統(tǒng)FCM算法流程
1.2 改進(jìn)模糊聚類算法
傳統(tǒng)的FCM 算法雖應(yīng)用廣泛,但其在對(duì)藥品數(shù)據(jù)資源進(jìn)行分析時(shí),對(duì)初始值較為敏感,導(dǎo)致收斂速度較慢,且在迭代過(guò)程中易陷入局部最優(yōu),影響了數(shù)據(jù)分析及預(yù)測(cè)的精度。因此,文中將繼續(xù)對(duì)FCM 算法進(jìn)行改進(jìn)[15-16]。改進(jìn)的算法流程如圖2所示。
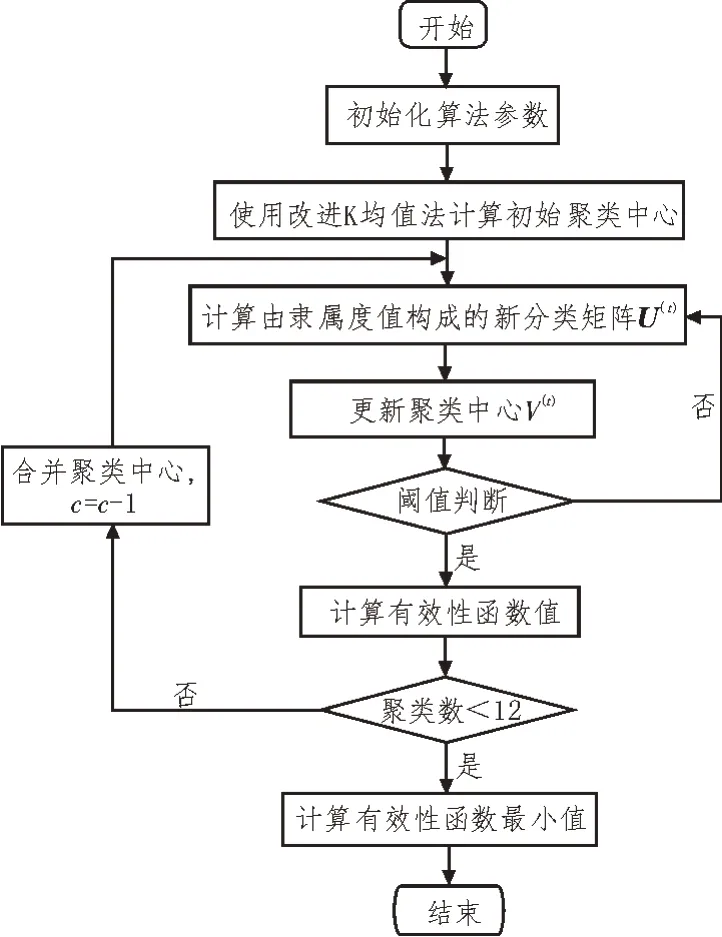
圖2 改進(jìn)的FCM算法流程
首先使用K 均值法(K-means)計(jì)算初始聚類中心,具體表達(dá)式為:
采用二維空間內(nèi)所有對(duì)象到樣本中心的平方差之和,作為K-means 的誤差判別E,而p為輸入樣本在二維空間的映射,mi則為Ci的聚類中心。引入該方法后,能夠有效提升FCM 的聚類中心初始化效果。
此外,為了度量FCM 算法的聚類效果,文中還引入了一種基于信息粒度的有效性函數(shù)。信息粒度可表征類間樣本的耦合性,且其主要包含耦合度Cd(c)和分離度Sd(c)兩個(gè)概念。其計(jì)算公式分別為:
基于式(2)-(3),可得到度量聚類效果的有效性函數(shù)為:
式(4)中,α為耦合度和離散度間的權(quán)重調(diào)節(jié)因子。
根據(jù)圖2 的流程,改進(jìn)后的FCM 會(huì)根據(jù)有效性函數(shù)GD 對(duì)分類效果進(jìn)行判別,使得類內(nèi)樣本間的距離盡量縮小,而類別間的聚類中心間距則盡可能擴(kuò)大。其中,類別間聚類中心的距離判別方法如下:
此外,為避免數(shù)據(jù)噪聲對(duì)模糊矩陣隸屬度的判別造成影響,文中還對(duì)目標(biāo)函數(shù)進(jìn)行了改進(jìn):
式(6)中,ηi為松弛因子,其降低了原損失函數(shù)對(duì)隸屬度的約束。該參數(shù)的表式如下:
其中,K為常數(shù)。則改進(jìn)后的FCM 算法參數(shù)更新方法如下:
2 方法實(shí)現(xiàn)
2.1 仿真實(shí)驗(yàn)設(shè)計(jì)
為了評(píng)估改進(jìn)后的模糊聚類算法性能,文中篩選了某藥品信息庫(kù)中的部分藥品作為數(shù)據(jù)集。具體的數(shù)據(jù)集參數(shù)為:樣本總數(shù)有450個(gè);藥品類別有3種;每類樣本個(gè)數(shù)為150 個(gè);藥品特征參數(shù)有8 個(gè)。
在評(píng)估改進(jìn)后的聚類方法對(duì)于藥品的聚類分析效率時(shí),使用了均方根誤差(SRMSE)作為評(píng)價(jià)指標(biāo)。其定義方式如下:
其中,Dp(x,y)為聚類后樣本在二維空間內(nèi)的位置坐標(biāo),c(x,y)是數(shù)據(jù)集中實(shí)際聚類中心的位置坐標(biāo),N則為該類藥品的樣本總量。
在進(jìn)行仿真分析時(shí),文中結(jié)合樣本規(guī)模對(duì)改進(jìn)FCM 算法的參數(shù)進(jìn)行了設(shè)置,如表1 所示。

表1 算法仿真過(guò)程中所用參數(shù)的設(shè)置
此次所使用的仿真軟硬件環(huán)境為:CPU 為i7-10750H;硬盤規(guī)格為1 TB 7200 rpm;系統(tǒng)內(nèi)存16 GB,操作系統(tǒng)為Windows10。顯卡采用P620,顯存4 GB,編程環(huán)境為Matlab 2019b。
2.2 算法仿真結(jié)果
為了評(píng)估算法的改進(jìn)效果,將其與傳統(tǒng)模糊聚類方法進(jìn)行了比較。兩種算法的迭代曲線如圖3所示。
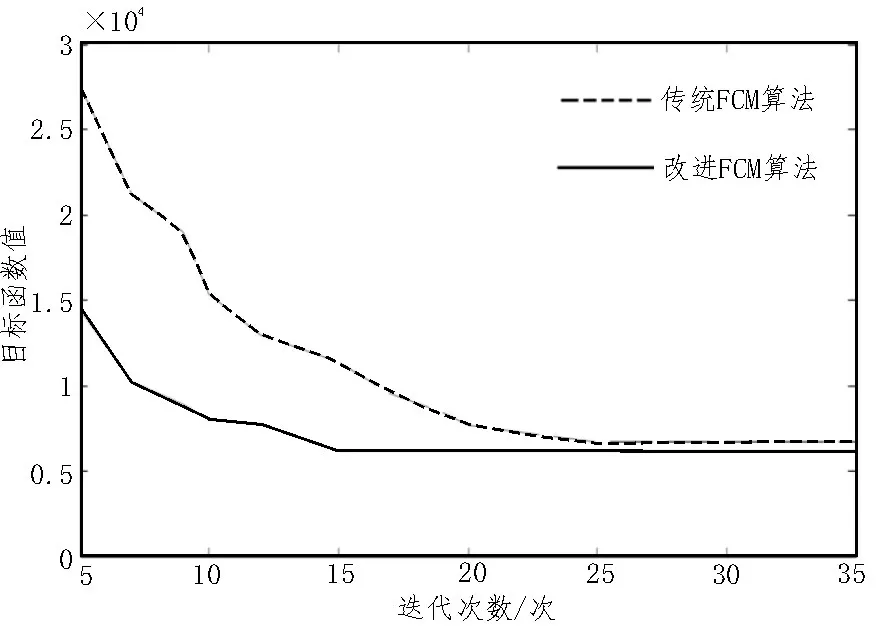
圖3 算法迭代曲線
圖3 顯示了算法在迭代過(guò)程中,目標(biāo)函數(shù)隨迭代次數(shù)的變化情況。從圖中可以看出,傳統(tǒng)算法在進(jìn)行25 次迭代之后,目標(biāo)函數(shù)值才趨于平穩(wěn);而該算法的目標(biāo)函數(shù)值僅迭代15 次便趨于穩(wěn)定,且迭代效率提升了約40%。由此可知,與傳統(tǒng)FCM 算法相比,改進(jìn)算法的目標(biāo)函數(shù)收斂速度較快。
根據(jù)實(shí)際的算法應(yīng)用場(chǎng)景,在對(duì)藥品數(shù)據(jù)進(jìn)行聚類分析前,由于類別數(shù)量c并非確定值,故還需根據(jù)算法的有效性函數(shù)值來(lái)確定。表2 給出了在仿真過(guò)程中,將數(shù)據(jù)集劃分為不同類別時(shí)的算法有效性函數(shù)值。可以看出,當(dāng)c=3 時(shí),算法能夠得到最優(yōu)的有效性函數(shù)值,約為0.421 3,而該類別數(shù)也與數(shù)據(jù)集的實(shí)際類別數(shù)相一致。
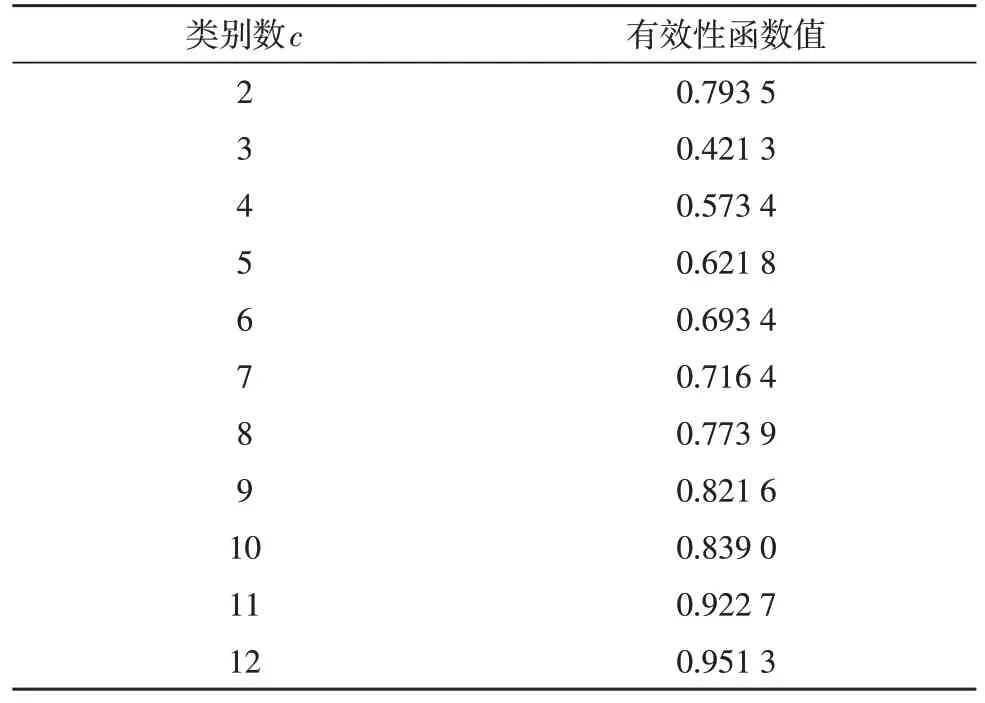
表2 不同類別數(shù)所對(duì)應(yīng)的有效性函數(shù)值
對(duì)數(shù)據(jù)集進(jìn)行聚類仿真實(shí)驗(yàn),得到的結(jié)果如圖4所示。
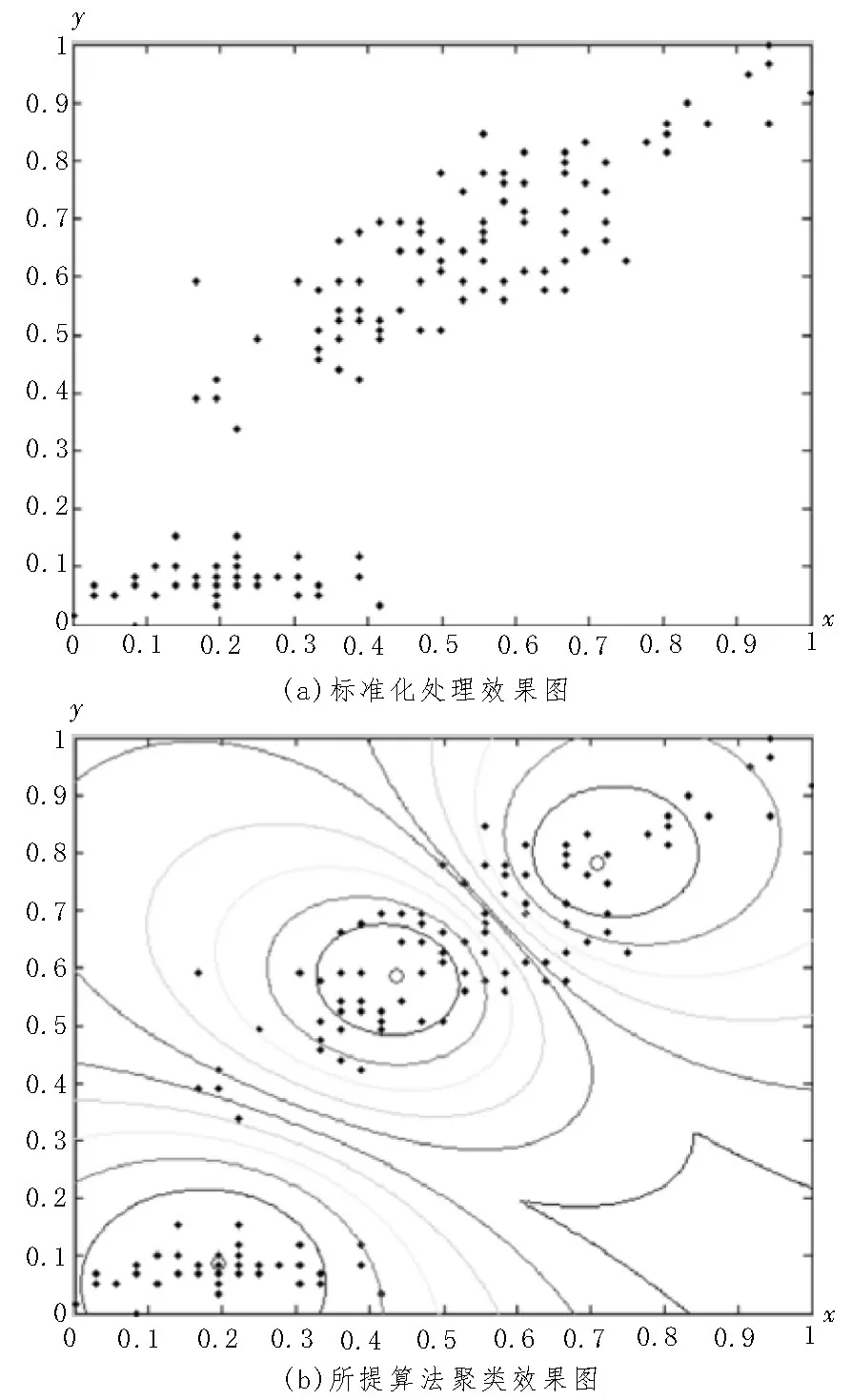
圖4 算法的樣本分類效果圖
圖4 中,將表1 的數(shù)據(jù)集進(jìn)行標(biāo)準(zhǔn)化處理,并映射至二維空間,即可得到圖4(a)所示的效果圖;而對(duì)圖4(a)中的數(shù)據(jù)使用文中算法進(jìn)行聚類,獲得的效果如圖4(b)所示。在圖4(b)中,空心圓圈為實(shí)際的聚類中心,圓弧線則為類別的邊界。從圖4(b)可以看出,圓弧線將所有的樣本劃分為3 類,且各個(gè)類簇之間并未存在交疊的現(xiàn)象。由此證明所提算法能對(duì)數(shù)據(jù)集中的所有數(shù)據(jù)進(jìn)行明確分類。
對(duì)于聚類算法,首先要將一堆無(wú)序的數(shù)據(jù)劃分為正確的類別。表3 給出了算法在50 次運(yùn)行過(guò)程中,能將實(shí)驗(yàn)數(shù)據(jù)正確劃分為3 類的統(tǒng)計(jì)結(jié)果。由表可知,該算法的正確率為94%,相較于傳統(tǒng)算法,提升了8%;而平均運(yùn)行時(shí)間降低至201 s,在傳統(tǒng)算法的基礎(chǔ)上縮短了27.17%。
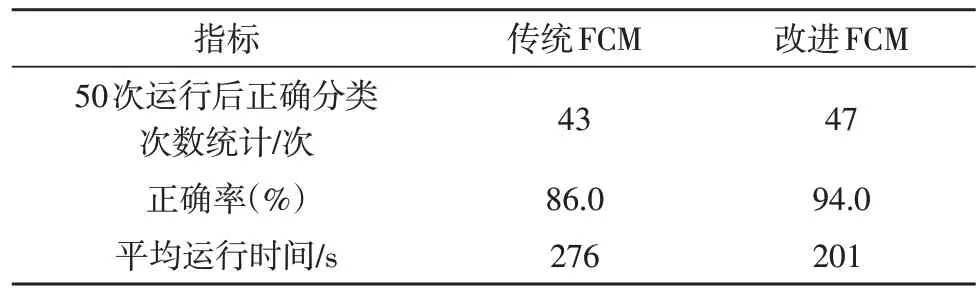
表3 算法聚類性能對(duì)比
表4 統(tǒng)計(jì)了在類別數(shù)c=3 時(shí),所有樣本的分類精度情況。對(duì)于450 個(gè)測(cè)試樣本,該算法的誤分類數(shù)量為23,分類錯(cuò)誤率為5.11%,RMSE 值為0.032 1。且相較于傳統(tǒng)FCM 算法,其錯(cuò)誤率下降了5.56%,RMSE 值則降低了79.61%。

表4 算法分類精度性能對(duì)比
3 結(jié)束語(yǔ)
文中對(duì)藥品的聚類分析與預(yù)測(cè)方法進(jìn)行了研究,通過(guò)引入新的聚類中心初始化機(jī)制及有效性函數(shù)改進(jìn)了傳統(tǒng)的FCM 方法。仿真結(jié)果表明,該算法對(duì)于聚類中心與樣本的分類精度均有顯著改善。而隨著我國(guó)醫(yī)藥領(lǐng)域數(shù)字化進(jìn)程的推進(jìn),所提算法將會(huì)有更為廣闊的應(yīng)用前景。
- 電子設(shè)計(jì)工程的其它文章
- 基于BN 算法的電力調(diào)度多源故障數(shù)據(jù)融合研究
- 基于分層聚合的電力系統(tǒng)不良數(shù)據(jù)自動(dòng)辨識(shí)
- 基于BIRCH 算法的配電網(wǎng)設(shè)備多源數(shù)據(jù)融合存儲(chǔ)技術(shù)研究
- 基于信息熵更新權(quán)重的數(shù)據(jù)自適應(yīng)聚類研究
- 基于負(fù)荷組合預(yù)測(cè)的配電網(wǎng)網(wǎng)架動(dòng)態(tài)變化識(shí)別方法
- 考慮負(fù)荷特性的電力系統(tǒng)低頻減載系統(tǒng)設(shè)計(jì)

