數學解題教學：從“一題多解”到“一題優解”

顧鋒 寧連華

摘 要：“一題多解”是數學解題的典型活動，也是解題教學的普遍追求。相較而言，對“一題優解”的認識與重視尚顯不足。在“一題多解”的基礎上進一步深度思考，對比、鑒別、篩選出最優化的解法，成為數學解題教學的應然追求。判斷一道題目最優化解法的主要標準有：簡單自然，效率為先，結構完美。

關鍵詞：高中數學；數學解題；解題教學；一題多解；一題優解

本文系江蘇省中小學教學研究第十四期“基于問題解決的數學抽象思維力培養實踐研究”（編號：2021JY14-L238）、江蘇省教育科學“十三五”規劃課題“TPACK視域下的卓越教師培養研究”（編號：B-a/2020/01/42）的階段性研究成果。

一、 “一題多解”的優越之狀與教學之失

“一題多解”是數學解題的典型活動，也是解題教學的普遍追求：教師適時地引導學生從不同的角度、用不同的思維方式觀察、聯想、分析，根據問題的特定條件探索出一系列解題思路，達到“一題多解”的效果。

丘成桐先生在北京師范大學附屬中學110周年校慶的演講中，也曾著力推崇“一題多解”。他說：“數學題的解法是有很多的，比如勾股定理的證明方法至少有幾十種，不同的證明方法幫助我們理解定理的內容。19世紀的數學家高斯，用不同的方法構造正十七邊形，不同的方法來自不同的想法，不同的想法導致不同方向的發展。所以，數學題的每種解法有其深厚的意義，你會領會不同的思想，我們要允許學生用不同的方法來解決。”［1］

可以說，“一題多解”廣受重視，其優越性不言而喻。“橫看成嶺側成峰，遠近高低各不同”的效果，不僅能幫助學生多角度地串聯知識、系統化地使用方法，而且能培養學生思維的廣闊性、發散性、靈活性等。試想，對同一個數學問題，從代數、幾何、三角、向量、復數、統計等不同的視角，探索出一系列解題思路（如函數ｆ（ｘ）＝3ｘ+3+2-ｘ最大值的求解［2］），無疑能激發學生發現、創造的強烈愿望，訓練學生對數學思想方法的嫻熟運用能力。

遺憾的是，“一題多解”也有它的教學之失：多數情況下停留在“一題多解”的境地，醉心于多種思路的呈現，缺少對各種方法優劣的評判、甄別與遴選，導致學生的解題水平遲滯于各種招式、技巧、模型的窠臼，難以觸及批判性思維、反省性思維、創造性思維等高層次思維活動，造成一種不應有的損失。這導致在練習和考試中，很多學生總是采用“笨拙”的方法解題，不能找到適合問題的最優解法，解題的質量和效率大打折扣。鑒于此，在“一題多解”的基礎上進一步深度思考，對比、鑒別、篩選出最優化的解法，成為數學解題教學的應然追求。

二、 “一題優解”的認識之乏與境界之求

相較于對“一題多解”的關注，數學教育界對“一題優解”的認識與重視尚顯不足，相關的研究比較匱乏。實際上，作為數學的一個重要分支，最優化方法（也稱作運籌學方法）廣為人知，即利用數學方法研究各種系統的優化途徑及方案。最優化方法已經廣泛地應用于設計、管理、控制等各個領域，很好地詮釋了最優化的魅力所在。遺憾的是，這種思想方法在數學學習的重要活動——數學解題中似乎并沒有得到很好的運用。這歸根結底在于對“一題優解”的認識不夠，自然也就不會有相應的追求。

所謂“一題優解”，是指從某個數學問題的多種解法中找到最優化的解法。著名數學教育家G．波利亞稱之為“最優解問題”。他認為：“解題需要做成本核算，在最優解問題中，既要到達目標，又要使成本最低，或利用率最高。如同給你一定的材料和操作構筑某種東西，但成本有限制，也許還有對材料和操作的使用的其他限制，解題者必須根據這些限制選定材料，科學地決策出最佳方案，制定施工程序（即操作序列），高效地完成任務。”［3］

“一題多解”是“一題優解”的前提與基礎，“一題優解”則是“一題多解”的推進與升華。

例1 如圖1，四邊形ABCD中，AB⊥CB，AD⊥CD，∠BCD=60°，且AD=3，CD=53，求BC的長。

無疑，這是一道有多種解法的題目，運用平幾法、解幾法、三角法、向量法等，都可以有多個路徑達到解題目標。只是，這林林總總的解法也是良莠不齊、特點各異：有的思路自然，但運算復雜；有的目標明確，但步驟繁繞；有的難以想到，但過程簡捷。

我們利用此題在高二學生中做了測試。選取高、中、低三個層次的學生各100名，要求8分鐘之內完成。結果發現：共出現了四類（平幾、解幾、三角、向量）18種解題方法，所有學生都選擇了某種方法來解決問題，僅有15名學生沒有得出最后的結論。

學生最普遍使用的方法是三角法（見圖2，解題過程省略），約占60%。

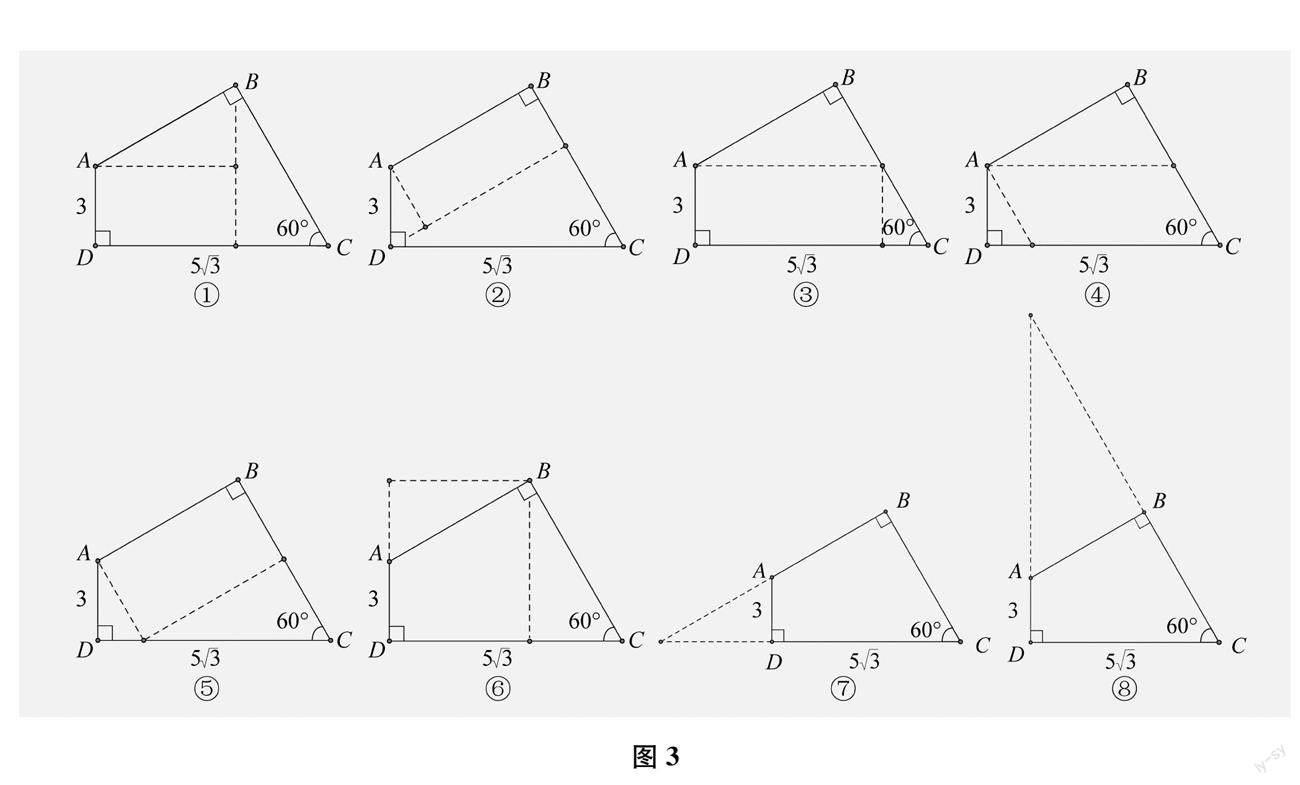
出現解法種數最多的則是平幾法思路，即基于圖形特點添加輔助線，主要運用勾股定理解決。這類方法多達8種（見圖3，解題過程省略），使用的學生約占32%。

此外，有少部分學生使用解幾法思路（建立平面直角坐標系）或向量法思路解決，兩者合計僅占8%。

應該說，本題形態各異的解法不可謂不精彩，對學生思維靈活性、深刻性的培養顯然大有裨益。但是，如果解題教學僅停留在各種方法的展現和賞析上，而不去比較不同方法的價值和優劣，是有遺憾的，甚至可以說是敗筆。

比較本題的多種解法不難發現，使用最多的方法（三角法）并非最優的解法。之所以使用此法的人數最多，恰恰是思維定式使然：思路自然但缺少必要的對比、判斷與決策，自然造成相對煩瑣的運算，解題效率也就較為低下。而8種平幾方法，多數舍近求遠，運算過程不簡單，屬于“花拳繡腿”式的招數，好看不好用；真正簡單自然、高效實用的方法就是最后的兩種往外延長四邊形的一組對邊得到兩個直角三角形的解法，它們才是本題的最優解法。但是，選用這兩種法的人數僅占2%。由此可見，解題方法優化意識與能力的培養在數學解題教學中亟待加強。

三、 “一題優解”的評判之難與推廣之利

毋庸置疑，一個問題“最優化的解法”有時候并不能很清楚地評判出來——種種解法殊途同歸、各有千秋，切入點不同，見解也不一樣，難以評定孰優孰劣，這就涉及“最優化的解法”的評判標準問題。著名數學家厄爾迪什曾說過：上帝是一本書，好的解法全在那本書上。對此，單壿教授評述道：上帝自然是沒有的，那本書其實就是由我們以及其他人的優雅解法組成的一本大書。［4］這些“優雅解法”或許各自有不同的特點，但也必定會形成一些共性的東西。以下是評判解法優劣的幾個主要標準：

（一） 簡單自然

好的解法應力求簡單自然。最好單刀直入，直接剖析問題的核心，不兜圈子、繞彎子，能一招解決就絕不用兩招，盡量減少廢招。［5］不自然的解法，不僅難看，也很難想到。一種奇怪的現象是：解題研究推崇一些看上去很漂亮的解題技巧，將某些構思巧妙、手法奇特的解法奉為圭臬。其實，這些解法可能只是少數人苦思冥想勾畫出來的個人“專利”，或者是解題者靈感閃現的產物，雖然有一定的創新性，但是難以復制；而且，大多數并不自然，鑲嵌著人為雕琢的痕跡。從學習者解題的效率來看，可以欣賞，但不應當自慚形穢，產生“技不如人”的自卑感。

例2 （2021年“八省聯考”數學卷第17題第2問）已知各項都為正數的數列{an}滿足an＋2＝2an＋1＋3an。若a1＝12，a2＝32，求{an}的通項公式。

解法一：因為an＋2＝2an＋1＋3an，所以an＋2-3an＋1＝-（an＋1-3an）。因為a1＝12，a2＝32，所以a2-3a1＝0，從而an＋1-3an＝0，即an＋1＝3an。所以，{an}是以12為首項，以3為公比的等比數列。因此，{an}的通項公式為an＝3ｎ-12。

解法二：因為數列{an}滿足an＋2＝2an＋1＋3an，所以其特征方程為x2＝2x＋3，解得x1＝-1，x2＝3，因此an＝A·（-1）n＋B·3n。又因為a1＝12，a2＝32，所以-A+3B=12，A+9B=32，解得A=0，

B=16。因此，{an}的通項公式為an＝3ｎ-12。

有人認為，上述兩種方法充分利用遞推關系an＋2＝2an＋1＋3an的特征，漂亮、優越，簡潔、有效。其實，解法一由an＋2＝2an＋1＋3an變換出an＋2-3an＋1＝-（an＋1-3an）談何容易，頗具技巧性和經驗性，并不能自然得出；解法二使用特征方程，背后又需具備多少課外拓展知識，對此不了解的學生只能望題興嘆。因而，這類所謂的“巧解妙招”不具有代表性和普遍性。

解法三：因為an＋2＝2an＋1＋3an，a1＝12，a2＝32，所以a3＝92……歸納猜測：an＝3ｎ-12。下面用數學歸納法證明：① 當n＝1時，a1＝12＝31-12，成立；② 假設當n≤k時，an＝3ｎ-12，則當n＝k＋1時，ak＋1＝2ak＋3ak-1＝2×3k-12＋3×3k-22＝3k＋1-12，即an=3n-12也成立。因此，an＝3ｎ-12。

這一方法著眼于從特殊到一般的歸納猜想，再用數學歸納法證明，簡單自然，很容易想到，也符合學生的思維習慣。有不同觀點認為，這一方法沒有思維含量，“套路化”明顯，顯得“笨拙”。實際上，像解法一、解法二等技巧性太強的解題方法，可能只是少數人的妙解、奇想；對于大多數解題者而言，像解法三這樣簡單自然的解題方法才應該是被廣泛接受和推崇的。

（二） 效率為先

解題需要拓展思維，也需要講究效率。方法雖然可行，但效率低下，則不能稱為好方法。正所謂“條條大路通羅馬，高效趨直方為優”，不追求效益的解法算不上好方法。尤其在各類考試中，一般都有時間限制，考查學生的綜合素養，題目不僅要做得對，還要做得快，講究解題的效率。

例3 （2022年新高考數學Ⅰ卷第18題第1問）記△ABC的內角A、B、C的對邊長分別為a、b、c，已知cos A1+sin A=sin 2B1+cos 2B。若C=2π3，求B。

本題最自然有效的解法應該是，將等式cos A1+sin A=ｓｉｎ 2B1+ｃｏｓ 2B右邊關于2B的三角函數化為關于B的三角函數，這樣與等式左邊對應起來，問題迎刃而解。具體如下：

解法一：由題設得ｃｏｓ A1+ｓｉｎ A＝2ｓｉｎ Bｃｏｓ B2ｃｏｓ2 B＝ｓｉｎ Bｃｏｓ B，于是cos Acos B=sin B+sin Bsin A，所以cos （A+B）=sin B。又因為A+B+C=π，C=2π3，所以sin B=cos（π -C）=12，因此B=π6。

調研發現，不少學生解答本題時，舍近求遠，繞來繞去，將問題做“難”、做“繁”了。

解法二：由cos A1+sin A=sin 2B1+cos 2B，得cos A（1+cos 2B）=sin 2B（1+sin A），得cos Acos 2B-sin Asin 2B=sin 2B-cos A，從而ｃｏｓ（A+2B）＝ｓｉｎ 2B-ｃｏｓ A。又因為C=2π3，所以A+B＝π3，即A＝π3-B，因此ｃｏｓπ3+B+cosπ3-B=sin 2B，從而cosπ3cos B-sin π3sin B+ｃｏｓπ3ｃｏｓ B+ｓｉｎπ3ｓｉｎ B＝ｓｉｎ 2B，所以ｃｏｓ B＝2ｓｉｎ B·ｃｏｓ Ｂ。又因為Ｂ∈0，π3，所以sin B=12，B=π6。

該方法直接“交叉相乘”，將本來角的倍數關系的暗示條件“淹沒”在等式中，使得后續三角關系的尋找、等式的變換、角的替換等運算要求增加不少，也使得解答的難度明顯上升，解題效率大大降低。

解法三：由二倍角公式知cos A1+sin A=cos2 A2-sin2 A2cos2 A2+sin2 A2+2sin A2cos A2，由“弦化切”得該式＝1-tan2 A21+tan2 A2+2tanA2=1-tanA21+tanA2=tanπ4-tan A21+tan π4tanA2=tanπ4-A2，sin 2B1+cos 2B=2 sin Bcos B2cos2 B=sin Bcos B=tan B。

由條件式得tan π4-A2=tan B。又因為C=2π3，所以A+B=π3，因此A、B∈0，π3，進而π4-A2∈π12，π4，所以π4-A2=B，從而B=π6。

該方法對等式兩邊分別使用二倍角公式，化成了tanπ4-A2與tan B兩個正切函數，應當說達到了目的，也能看出解題者的良苦用心，但是變換出tanπ4-A2的過程需要的信息量、運算量實在太大，至少是解法一計算量的兩三倍。這樣粗淺“蠻干”的方法不應鼓勵。

（三） 結構完美

眾所周知，數學具有深邃的結構美。諸如科赫曲線、希爾伯特曲線、248維晶體對稱結構等，都給我們展示了數學的結構魅力。在解題時注重呼應數學的結構美，往往能使問題完美解決。愛因斯坦就是注重結構思維的典型代表，其“相對論”理論體系正是得益于其一貫的完整、對稱的結構思想方法。一些經典的問題探求也體現了結構美的思想。例如勾股定理的證明、代數基本定理的證明、楊輝三角形的各種性質等，都很好地體現了對數學結構美的認識與欣賞。注重從數學結構美的特點切入，構思出的解法往往能提升解題者對數學的理解與感悟能力。

如對前述例3，如果注意到條件式的結構特點，利用“同構函數”思想，則可得到下述解法：

解法四：由cos A1+sin A=sin 2B1+cos 2B，可得sinπ2-A1+cosπ2-A=sin 2B1+cos 2B。令f（t）=sin t1+cos t，ｔ∈（0，π），則fπ2-A=f（2B）。而f（t）=2 sin t2cost22cos2t2=tant2，在（0，π）上單調遞增。又因為C=2π3，所以A+B=π3，因此A、B∈0，π3，進而π2-A2∈π6，π2，2B∈0，2π3，從而π2-A=2B，所以B=π2-（A+B）=π6。

該方法利用“同構函數”的思路，有一定的靈活性和創新性，也能看出解題者利用所學知識解決問題的意識與能力，是比較智慧的一種解法。

數學中的基本結構類似那種成批制造產品的機器，短時間內能夠制造出許多件，并且每一件都造得相當完美。數學解題也是這樣：充分把握并利用某類數學問題的基本結構特點，往往能獲得漂亮、有效的解題方法。

例4 因式分解：

（1） （x+y+z）3-x3-y3-z3；

（2） （a+b）5-a5-b5；

（3） （x-y）5+（y-z）5+（z-x）5；

（4） （2x+3y）3+（3x+2y）3-125（x+y）3。

如果不注意觀察各式的結構特點，不充分利用結構美的思想尋找解題方法，而一味地展開、組合、分解，則會使解題過程煩不勝煩。如果注意到每個式子的結構美以及其元素的對稱性，就可直接發現各自的因式，簡潔、完美地使問題得解。

具體來說，（1）的因式有x+y、y+z、z+x，（2）的因式有a、b、a+b、a2+b2+ab，（3）的因式有x-y、y-z、z-x、x2+y2+z2-xy-yz-zx，（4）的因式有2x+3y、3x+2y、x+y。由此，只需再依據式子的恒等性，利用“特殊值法”，即可確定分解因式后的系數，從而完成因式分解。

應當說，利用題目本身所具備的結構美構思解法，在數學解題中比比皆是，應當成為數學解題的一種基本思想，也是判斷解法是否優越、尋求“最優解”的一個重要標準。

當然，判斷一道題目的解法是否最優化確實有相當的難度，以上幾種方法僅提供了一些觀察視角。題目千差萬別，解法也琳瑯滿目，還應該根據具體情境，結合實際情況綜合判斷，選擇最優化的解法。

總之，從“一題多解”走向“一題優解”，應當作為數學解題教學的境界追求。盡管對某個問題探尋出多種解法已非易事，評判、甄選出其中的“最優解”自然更加困難，但是具備了這樣一種意識，在持續不斷的探索嘗試中，學生的“一題優解”能力必將不斷提高。

參考文獻：

［1］ 丘成桐.學問、文化與美——在北京師范大學附屬中學的演講［J］.人民教育，2011（24）：33.

［2］ 丁里順.貫通學科分支，形成整體認識——一道根式函數最值問題的多解教學［J］.教育研究與評論（中學教育教學），2022（11）：82-87.

［3］ G.Polya.How To Solve It： A New Aspect of Mathematical Method［M］.New Jersey：Princeton University Press， 1973：20.

［4］［5］ 單壿.解題研究［M］.上海：上海教育出版社，2013：183，183.