問題導學法在小學數學教學中的實施路徑

劉光收

“問題導學法”主要指的是教師在教學過程中根據具體的教學內容提出一些問題，讓學生依據這些問題展開思考和探究，以數學獨有的思維方式去發現問題、提出問題、探究問題，從而有效地解決問題，切實提升學生分析問題和解決問題的能力，落實核心素養的發展。學生在問題解決的過程中獲得知識、建構知識、全面內化，提升自身的學習素養，進而達成對知識的創造性理解，借此獲得更深遠的發展。

一、注重問題設置環節

在小學數學教學過程中，教師在實施問題導學法時應關注問題設置環節，根據具體的教學內容設置相關問題，并保證整個教學過程中每個階段所設置的問題都緊密相連，逐漸引導學生實現對所學知識內容的探究，獲得對知識的深層次理解及感悟。這樣才能夠充分發揮問題導學法的價值和作用，驅動學生獲得較為深遠的發展。

以人教版小學數學《百分數（一）》一課為例，本課需要學生學習百分數與分數、小數互化以及使用百分數知識解決生活實際問題。因此，教師在設置問題時就可以從以下幾個方面著手。

首先，教師播放足球比賽視頻，創設這樣一個生活情境：德國隊在比賽中獲得了一次罰點球的機會，如果你是這個隊的教練，你準備派哪一名隊員去罰這個點球呢？請小組之間互相討論，得出結果并說明理由。教師以這樣一個與學生興趣愛好相關的足球世界杯為切入點，為學生創設生活化的教學情境，并提出“應該派哪一名球員去罰點球”這一問題，促使學生積極思考，獲得更豐富的知識探究經驗，讓學生的討論更切合實際。

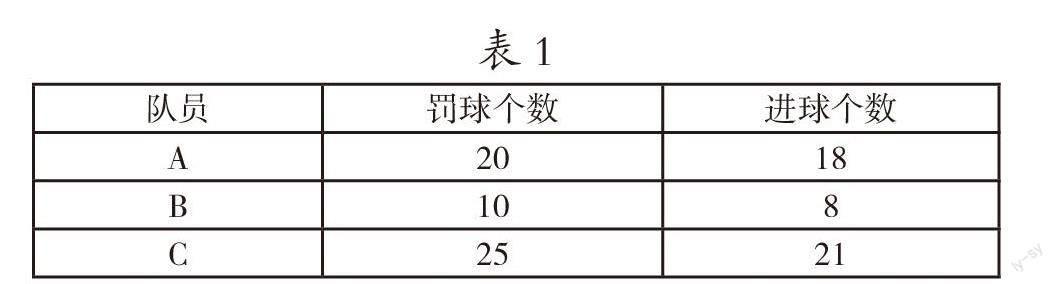
其次，教師可以引導啟發，讓學生深層次探究問題。學生經過討論得出了不同的答案，并且針對自己的答案有自己的論證。在這一環節，教師引導學生嘗試算一算每個隊員的進球率。對此，教師可以為學生展現德國隊成員罰點球的情況，如表1所示。

借助這一表格，算出隊員的進球率，分別為18/20、8/10、21/25，算出進球率之后，就要比較它們的大小，教師便可以順勢引入“百分數”，讓學生將分數通分，變成分母為一百的數，分別為90/100、80/100、84/100。教師再一次詢問學生：“這三個分數分別表示什么含義呢？你們現在知道派誰去罰球了嗎？”在這一環節，教師通過讓學生算進球率的方式，將分數變成分母為一百的數，進而引入“百分數”的概念，幫助學生獲得對本節知識內容的初步探究。在這個過程中，教師始終以“派誰去罰點球”為中心問題，讓學生展開多元化的實踐探究，讓問題與問題之間形成較為嚴密的邏輯關系和科學的問題鏈。而學生也能夠根據自身已有的分數通分知識展開積極思考，實現啟發式學習，逐漸提升了數學思維。

最后，教師可以讓學生展開拓展訓練。學生借助“百分數”得出了應該派誰去罰點球之后，教師可以讓學生再一次串聯自身的知識，分析百分數與分數之間的區別和聯系。在這一過程中，為了讓學生的探究方向更明確，教師可以引入與生活息息相關的例子，讓學生感受分數與百分數的異同。

二、注重問題探究環節

教師在實施問題教學法時，應注重學生對問題的探究，讓學生根據具體的問題去探究相關知識內容，達成對所學知識的有效理解及內化，豐富數學思維，最終實現長遠發展。以人教版小學數學《圓的周長》一課為例，本課教學重點是讓學生在實踐中掌握圓周長的計算公式及圓周率的基本意義。教師可以從以下幾個方面著手實施問題導學法，驅動學生探究本課知識內容。

首先，教師可以為學生創設情境，呈現具體的探究問題。比如，教師可以借助多媒體呈現學生玩丟手絹游戲的活動照片，讓學生思考跑這一圈到底有多長，計算自己跑一圈的長度，從而引入本節課教學內容——圓的周長，讓學生以飽滿的情緒展開對這一問題的探究。

其次，教師可以引導學生想一想，要想計算跑一圈的長度，應該從哪里找到突破口，而后讓學生展開小組合作，將手中的圓片（提前準備）比作游戲活動中的“圈”，思考怎樣求出它的長度。有的小組經過討論得出以下兩個方法：第一，用繩子繞圓片一圈，再測量繩子的長度；第二，將圓片在紙上滾一圈，而后測量滾一圈的長度。教師對學生的回答表示認同，并質疑：這種方法只適用于小圓圈的計算，如果計算現實生活中很大的圓圈廣場，又應該怎么辦呢？再一次讓學生陷入思考。在這一過程中，學生的思維得到了進一步發散，獲得了創造性的成果。在學生得出小組探究成果后，教師先表示認同，再質疑，讓學生明白這種周長計算方法的局限性，然后進一步展開實踐探究，激活學生的求知欲。

再次，教師可以讓學生猜一猜圓的周長可能與什么因素相關（半徑、直徑），如果有關，是一種什么樣的關系（求出數量關系）。教師借助問題，讓學生明白了探究的方向。而學生可以通過測量計算的方式，得出圓的周長與半徑和直徑存在的數量關系，如“圓的周長與圓直徑的比值大概是3點多（π），圓的周長與圓半徑的比值為2π”。根據學生得出的結論會發現，這里的“3點多”和“1.5左右”都指向一個重要的數學知識點——“π”。對此，教師可以順勢引入“圓周率”的相關故事，讓學生了解圓周率是一個名叫祖沖之的中國人發現的，而“圓周率”就等于圓的周長除以直徑。“π”約等于3.14，這就又回到了學生探究的點——“3點多”和“1.5左右”，學生的探究性思維就形成了前后閉環。

最后，教師可以提出一些研究性的問題：

1.請分別求出直徑為10厘米和半徑為10厘米的圓的周長。

2.在求解之后會發現同樣是10厘米，但是為什么結果大相徑庭呢？

3.只要圓的直徑越大，圓周率就越大，這句話是否正確呢？

這三個問題是環環相扣的關系，雖然看起來比較簡單，但是對一些審題馬虎的學生來說是很容易出錯。前兩個問題是讓學生認真審題，避免在計算過程中出現半徑和直徑混用的情況，進一步增強學生的審題意識；第三個問題是讓學生研究圓周率的性質和概念，進一步加深對圓周率知識的理解。所以三個問題是循序漸進的關系，能夠進一步促進學生理解和掌握所學知識，達到舉一反三的效果，最終提升學生的數學核心思維。

三、注重問題解決環節

教師在實施問題導學法時還應注重問題的解決，重在指導學生利用所學知識解決實際問題，整體提升其解決問題和統籌規劃的能力，讓學生在探尋相關知識內容后，實現對知識的綜合性應用，進而在腦海中實現對相關知識體系的全盤建構。

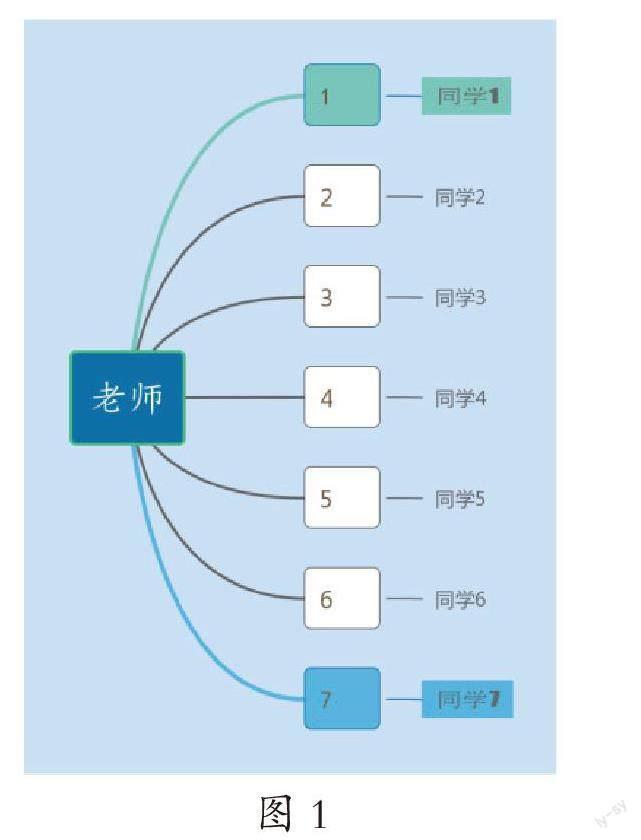
以人教版小學數學《打電話》一課為例，教師可以根據這一綜合實踐活動來培養學生運用數學知識解決實際問題的能力，幫助學生逐層構建數學模型，實現對所學知識的有效理解及內化。首先，教師可以為學生創設“打電話”的情境，探尋優化方案。具體情境如下：學校準備開展一場校際籃球友誼賽，體育教師必須盡快通知我校籃球隊的7名同學，如果用打電話的方式，每分鐘通知一人，一共需要多長時間呢？借助這一情境，讓學生嘗試設計體育教師打電話的方案，并嘗試繪制方案圖，如圖1所示。

其次，根據學生初步得出的方案，教師可以詢問學生，是否可以進一步優化，減少教師打電話的時間。學生經過思考，得出以下方案，如圖2、圖3、圖4所示。

在學生得出一系列的方案之后，教師可以再一次詢問學生：“這三組方案與第一組方案相比，時間大大縮減了。那么這三種方案中哪一種用時最少呢？”引導學生反思自己設計的三組方案，嘗試選出最佳方案。而學生在反思的過程中也能夠有新的發現，如學生發現方案二用時最短，但是在同學1通知了同學4和同學5后，同學4或同學5可以再通知同學7，這樣就能又節約一些時間，進而建立模型，如圖5所示。

在建立了這樣一個完整的模型后，教師可以提出問題：如果還要加入8名同學參與啦啦隊，教師想盡快通知這15個人，又應該怎樣安排呢？學生已經建立了模型，在此基礎上便會繼續生成方案圖。教師可以根據學生繪制的方案圖展示以下表格，讓學生完成，如表2所示。

學生根據自己繪制的方案，結合表格中的數據，會發現以下結論：時間增加一分鐘，新接到通知的人數是前面接到通知人數的兩倍；時間增加一分鐘，總人數也是前面總人數的兩倍……

學生得出的推論大致相似，那么教師就要逐漸引導學生得出“第幾分鐘知道消息的總人數就是幾個2相乘的積。”比如，第一數列是“2×1”，第二數列是“2×2”，第三數列是“2×2×2”等。

最后，學生已經完全摸索出了規律，那么教師就可以為學生出示以下題目，讓學生嘗試解答：

1.如果要通知52名小區人員做志愿者，每人1分鐘，至少需要多少分鐘呢？

2.有一種樹原來只有一節樹枝，第一年會長出一個新枝，第二年每一個樹枝會再長出一個新枝，第三年每節樹枝又會繼續長出一個新枝，這樣，第五年一共會有幾節樹枝呢？

在這一環節教師更關注學生對問題的解決，通過解答問題的方式，讓學生逐漸建立數學模型，將簡單的問題逐漸細化，深化學生對知識的理解，驅動學生主動探索，最終形成模型思維，有利于學生的長遠發展。

四、結語

綜上所述，教師在實施問題導學法時應關注問題設計的整個過程，如問題設置環節、問題解決環節以及問題探究環節。每一個環節都要細化，根據具體的教學內容，有側重點地實施，驅動學生主動思考問題，引導其展開分析、探究及優化，最終落實數學核心素養的培育。