無窮型雙圈圖的零度

苗豐 王龍

文章編號(hào)：1003?6180（2023） 03?0001?04

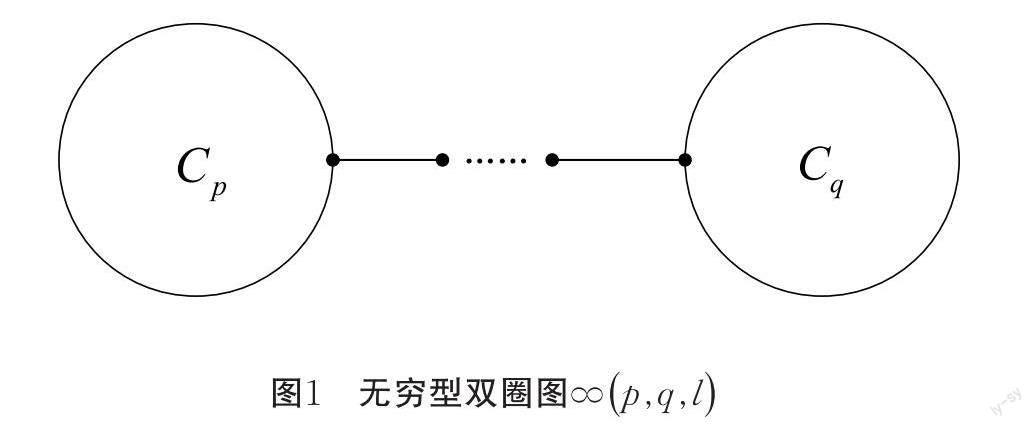
摘? 要：無窮型雙圈圖[∞p，q，l]是通過連接兩個(gè)不相交的圈[Cp]和[Cq]的一個(gè)頂點(diǎn)與一條路徑[Pl]所得到的，其中，[Cp]和[Cq]是圈長分別為[p]，[q]的兩個(gè)基本圈，路徑[Pl]的長度為[l-1].圖的零度[ηG]是指圖[G]的鄰接矩陣的0特征值的重?cái)?shù).本文刻畫了無窮型雙圈圖[∞p，q，l]的零度.

關(guān)鍵詞：零度；無窮型雙圈圖；匹配數(shù)

[? ?中圖分類號(hào)? ? ]O157.6 [? ? 文獻(xiàn)標(biāo)志碼? ?]? A

The Nullity of Infinity-Type Bicyclic Graphs

MIAO Feng，WANG Long

（School of Mathematics and Big Data， Anhui University of Science and Technology，

Huainan 232001， China）

Abstract：The infinity-type bicyclic graph [∞p，q，l] is obtained from two disjointed cycles [Cp]and [Cq] by connecting one vertex of [Cp]and one vertex of [Cq] with a path [Pl]， where [Cp] and [Cq] are the two basic cycles with cycle lengths of [p] and [q] respectively， and path [Pl] has a length of [l-1]. The nullity of [G]， denoted by [ηG]， is the multiplicity of the eigenvalue zero of the adjacency matrix of the graph [G]. This paper characterizes the nullity of the infinity-type bicyclic graphs.

Key words： nullity； infinity-type bicyclic graphs； matching number

在化學(xué)領(lǐng)域，圖的零度問題有著重要且廣泛的應(yīng)用.在Hückel分子軌道模型中，若分子圖[G]有[ηG>0]，則相應(yīng)的化合物具有高度反應(yīng)性和不穩(wěn)定性，或不存在.[1，2]此外，圖的零度在數(shù)學(xué)領(lǐng)域也意義重大，它和鄰接矩陣[AG]的奇異性相關(guān).若一個(gè)圖的鄰接矩陣[AG]是奇異的，那么這個(gè)圖被稱為奇異的，反之這個(gè)圖被稱為非奇異的.在這樣的背景下，人們對(duì)圖的零度的研究主要通過特定的圖類著手進(jìn)行.2008年袁西英[3]等人確定了所有[n]階（[n≥6]）雙圈圖的零度集合是[0， n-4].2009年Guo[4]等人刻畫并給出了單圈圖和匹配數(shù)之間的關(guān)系.2016年Sa Rula[5]等人刻畫并給出了雙圈圖與匹配數(shù)之間的關(guān)系.本文考慮的圖都是有限的、無向的和簡單的.

圖[G]是一個(gè)具有[nG]個(gè)頂點(diǎn)和[eG]條邊的連通圖.圖的基本圈數(shù)[cG=eG-nG+1]，若[cG=0]，圖[G]為一個(gè)樹；若[cG=1]，圖[G]為單圈圖；若[cG=2]，圖[G]為雙圈圖.圖[G]的鄰接矩陣記為[AG]，它是一個(gè)[n]階矩陣[aijn×n]，當(dāng)[vi]與[vj]鄰接時(shí)，[aij=1]，否則，[aij=0].鄰接矩陣[AG]的0特征值的重?cái)?shù)稱為圖[G]的零度，圖[G]的零度用[ηG]來表示.顯然，[ηG=n-rAG]，這里的[n]為[G]的階數(shù)，[rAG]為[AG]的秩.[G]中的匹配是一組非相鄰的邊，如果[M]是匹配的，則與[M]的邊相關(guān)的每個(gè)頂點(diǎn)都被[M]覆蓋.完美匹配是覆蓋[G]的每個(gè)頂點(diǎn)的匹配，最大匹配是覆蓋圖[G]中盡可能多的頂點(diǎn)的匹配.用[mG]來表示[G]的匹配數(shù)，也就是[G]的最大匹配的邊數(shù).本文刻畫無窮型雙圈圖[∞p，q，l]的零度.

1 相關(guān)引理

設(shè)[G=V，E]是一個(gè)[n]階簡單圖，[VG=v1，v2…vn]是圖[G]的頂點(diǎn)集，[EG=e1，e2…em]是圖[G]的邊集.[vG]和[eG]分別代表圖[G]的點(diǎn)數(shù)和邊數(shù).

[Cp]和[Cq]是圈長分別為[p]，[q]的兩個(gè)基本圈， 通過將兩個(gè)不相交的圈[Cp]和[Cq]的一個(gè)頂點(diǎn)與一條路徑[Pl]連接的連通圖稱作無窮型雙圈圖[∞p，q，l]. 其中，路徑[Pl]的長度為[l-1].（圖1）.

2016年Sa Rula[4]等人給出以下結(jié)果，從而決定了雙圈圖[∞p，q，l]的零度與其匹配數(shù)之間的關(guān)系.

引理1[5] 在無窮型雙圈圖[∞p，q，l]中，設(shè)[G∈∞p，q，l]，則關(guān)于圖[G]的零度與其匹配數(shù)之間的關(guān)系有以下結(jié)論：

（1）[ηG][=][nG][-][2mG][-1]當(dāng)且僅當(dāng)[G]滿足以下任一條件：

（i）[p]或[q]其中一個(gè)滿足[2mod4]，另一個(gè)為奇數(shù)，[l]是偶數(shù)；

（ii）[p，q，l≡1mod2]，[p≡qmod4].

（2）[ηG=][nG-2mG+1]當(dāng)且僅當(dāng)[p]或[q]，其中一個(gè)滿足[0mod4]，另一個(gè)為奇數(shù)，[l]是奇數(shù).

（3） [ηG=nG-2mG+2]當(dāng)且僅當(dāng)[G]滿足以下任一條件：

（i） [p]或[q]其中一個(gè)滿足[0mod4]，另一個(gè)滿足[2mod4]，[l]是偶數(shù)；

（ii） [p，q≡0mod4].

（4） 當(dāng)[G]滿足除以上三種情以外的其他情況時(shí)，[ηG=nG-2mG].

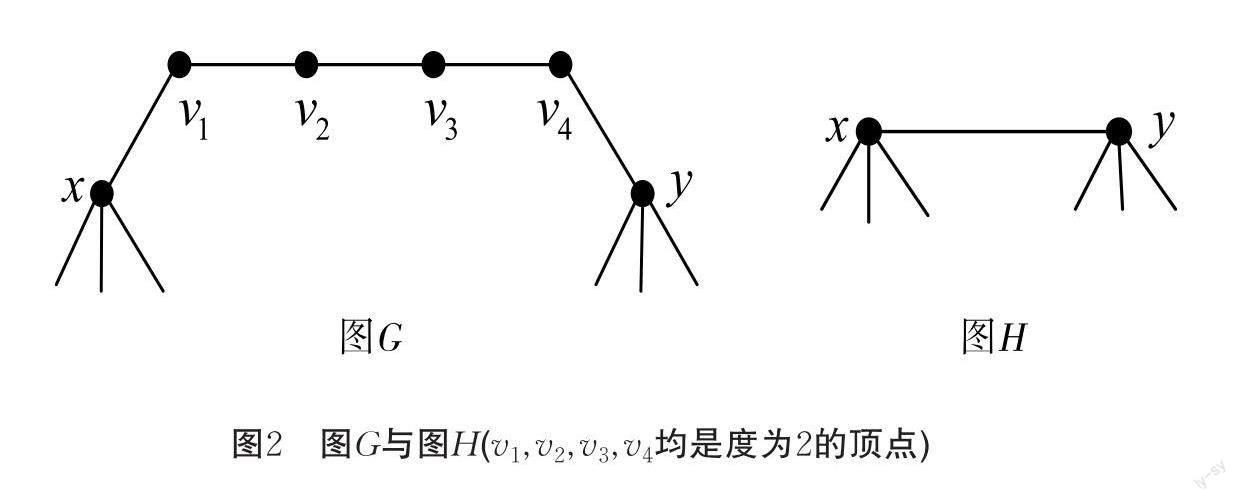
引理2[6] 在圖[G]中，一條有四個(gè)度為2的頂點(diǎn)的路徑用一條邊替代時(shí)，得到圖[H]，則有[ηG=ηH]（圖2） .

2 主要結(jié)果

無窮型雙圈圖[∞p，q，l]是通過將兩個(gè)不相交的圈[Cp]和[Cq]的一個(gè)頂點(diǎn)與一條路徑[Pl]連接所得到的雙圈圖，其中，[Cp]和[Cq]是圈長分別為[p]，[q]的兩個(gè)基本圈，路徑[Pl]的長度為[l-1].

首先，給出幾個(gè)有限頂點(diǎn)的圖的零度，可通過計(jì)算圖的鄰接矩陣特征值得到，也可以通過引理1導(dǎo)出.

引理3 若[G∈∞p，q，l]，其中，[p，q∈3，4，5，6]，[l∈1，2，3，4，5]，則其零度如表1所示.

引理4 在無窮型雙圈圖[∞p，q，l]中，[p=][4c+d]，[q=][4e+f]，[l=][4g+h]，[d，f∈] [3，4，5，6]，[h∈1，2，3，4，5]，[c，e，g]為非負(fù)的整數(shù).則有[η∞p，q，l=η∞d，f，h].

證明 由引理2知，在無窮型雙圈圖[∞p，q，l]中，[l=4g+h]，[h=1，2，3，4，5]，[g]為非負(fù)的整數(shù)時(shí)，有[η∞p，q，l=η∞p，q，h].

又由引理1知，在無窮型雙圈圖[∞p，q，l]中，在不同情況下，圖的零度與匹配數(shù)之間的關(guān)系式為[η∞p，q，l=][n∞p，q，l][-2m∞p，q，l+a].其中，[a]的值是確定的，[Cp]或[Cq]的圈長每增加[4c]或[4d]，則匹配數(shù)隨之增加[2c]或[2d]，零度不發(fā)生改變，即在無窮型雙圈圖[∞p，q，l]中，[p=4c+d]，[q=4e+f]，[c，e]為非負(fù)的整數(shù)，[η∞p，q，l=η∞d，f，l].綜上，引理4得證.

定理1 在無窮型雙圈圖[∞p，q，l]中，設(shè)[G∈∞p，q，l]，則關(guān)于圖[G]的特定零度與其對(duì)應(yīng)的情況有以下結(jié)論：

（1） [ηG=0]當(dāng)且僅當(dāng)[G]滿足以下任一條件：

（i）[p+q≠0mod4]，[p，q≠0mod4]；

（ii） [p+q=0mod4]，且[l=0mod2].

（2） [ηG=1]當(dāng)且僅當(dāng)[G]滿足以下任一條件：

（i） [p]或[q]其中一個(gè)滿足[0mod4]，另一個(gè)滿足[1（mod2）]；

（ii） [p]或[q]其中一個(gè)滿足[0mod4]，另一個(gè)滿足[0（mod2）]，且[l=1mod2]；

（iii）[p，q≠0mod4]，[p+q=0mod4]，且[l=1mod2].

（3） [ηG=2]當(dāng)且僅當(dāng)[G]滿足以下任一條件：

（i） [p≡q≡0mod4]且[l=0mod2]；

（ii）[p]或[q]其中一個(gè)滿足[0mod4]，另一個(gè)滿足[2mod4]，且[l=0mod2].

（4） [ηG=3]當(dāng)且僅當(dāng)[p，q≡0mod4]且[l≡1mod2].

證明 充分性由引理1以及圖的鄰接矩陣秩的計(jì)算可得，對(duì)于任意特定的雙圈圖[∞p，q，l]的零度，可以通過引理1中[p，q，l]所滿足的情況對(duì)應(yīng)的關(guān)系式[η∞p，q，l=n∞p，q，l-2m∞p，q，l+a]得到.

必要性由引理3和引理4可得，引理3描述了無窮型雙圈圖[∞p，q，l]的零度為[0，1，2，3]時(shí)其對(duì)應(yīng)的特定無窮型雙圈圖，結(jié)合引理4，可以刻畫出零度為[0，1，2，3]時(shí)所對(duì)應(yīng)的所有無窮型雙圈圖[∞p，q，l]的特征，即[p，q，l]所滿足的條件.

參考文獻(xiàn)

[1]Atkins P， De Paula J. Physical Chemistry[M]. New York：Oxford University Press， 2006.

[2]Cvetkovi? D M ， Gutman I M . The algebraic multiplicity of the number zero in the spectrum of a bipartite graph[J]. Mat Vesnik， 1972（9）：141–150.

[3]袁西英，單海英，劉穎.雙圈圖的零度集合[J].同濟(jì)大學(xué)學(xué)報(bào)：自然科學(xué)版，2008（03）：397-401.

[4]Guo J M， Yan W G， Yeh Y N. On the nullity and the matching number of unicyclic graphs[J]. Linear Algebra and its Applications， 2009， 431（8）：1293-1301.

[5]Sa Rula， A Chang， LI Jianxi. The nullity of bicyclic graphs in terms of their matching number[J]. Journal of Mathematical Research with Applications， 2016， 36（6）：12.

[6]Wang L， Fang X， Geng X. Graphs with nullity [2cG+pG-1][J]. Discrete Mathematics， 2022， 345（5）： 112786.

[7]彭?xiàng)睿@亞，朱娜.幾類正慣性指數(shù)為2的圖的刻畫[J].牡丹江師范學(xué)院學(xué)報(bào)：自然科學(xué)版，2021（01）：1-6.

[8]Chang S， Tam B S， Li J， et al. Graphs G with nullity [2cG+pG-1][J]. Discrete Applied Mathematics， 2022， 311： 38-58.

[9]姜娟，王龍.擬完全圖的秩、正負(fù)慣性指數(shù)和零度[J].牡丹江師范學(xué)院學(xué)報(bào)：自然科學(xué)版，2021（03）：6-8+13.

[10]Ma X， Wong D， Tian F. Nullity of a graph in terms of the dimension of cycle space and the number of pendant vertices[J]. Discrete Applied Mathematics， 2016， 215： 171-176.

編輯：琳莉