阿基米德三角形的一個性質與圓錐曲線光學性質的邂逅*

廣州大學附屬中學(510006) 曹路路 朱驚濤

1. 引言

圓錐曲線的弦與過弦的端點的兩條切線所圍成的三角形叫做阿基米德三角形. 阿基米德三角形是高中解析幾何中一個經典的雙切線模型,在2021 年全國乙卷、2019 全國3卷、2018 年浙江卷、2012 年福建卷與江西卷、2008 年山東卷與江西卷、2007 年江蘇卷和2006 年全國ⅠⅠ卷中均出現與之相關的高考試題. 試題呈現方式主要以拋物線和雙曲線為載體,以阿基米德三角形為背景,考察學生在解決直線與圓錐曲線位置關系時的運算、邏輯推理、數學抽象思維等能力. 目前有諸多作者對其性質以及在高考試題背景方面進行了比較多的研究. 例如方亞斌老師文[1]中詳細的列出了其各種性質并給出了詳細的證明;況思怡、姚運國兩位老師在文[2]中結合高考試題詳細地分析了阿基米德三角形在高考試題中的命題方式與解題策略;另外還有王海燕老師的文[3]、谷留明老師的文[4]等眾多文章. 除此以外還有唐明超、楊亞平兩位高校老師在文[5]中基于文獻分析的視角詳細地對目前有關阿基米德三角形的研究文獻進行了分類分析和總結. 但是筆者在眾多文獻中,發現鮮有作者深度探究阿基米德三角形與圓錐曲線光學性質的內在聯系. 本文從拋物線中阿基米德三角形的一個與角度相關的性質出發,揭示了該性質與拋物線的光學性質的關系. 并將這一結論推廣到橢圓和雙曲線中去,重點從幾何角度探討阿基米德三角形這一性質與圓錐曲線光學性質的內在聯系,使得阿基米德三角形這一經典問題在教學和試題命制中煥發新的生命力.該結論的推廣與證明對我們的日常教學和命題研究有一定的價值.

2. 拋物線中的阿基米德三角形的一個性質及其證明

阿基米德三角形有許多性質,本文以拋物線為例,介紹其中一個與角度相關的性質.

題目1如圖1,過拋物線y2= 2px(p＞0)上任意兩點A、B分別作兩條切線相交于點P,F是拋物線的焦點,連接FP,FA,FB,則恒有∠PFA=∠PFB.

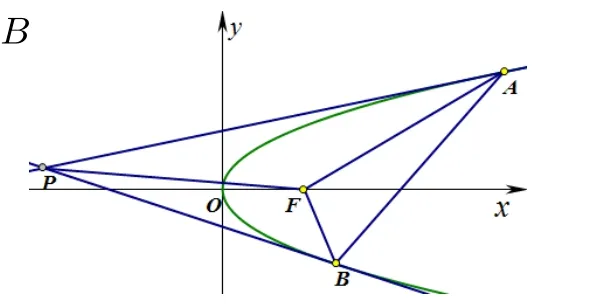
圖1

證法二注意到點F是焦點,PA是過點A的切線,聯想到拋物線的光學性質, 從點F發射的光線射到點A處, 其反射光線與x軸平行, 而這一性質等同于切線PA平分∠EAF(如圖2),基于此,再結合拋物線定義,從而該題結論得證.

圖2

3. 圓錐曲線的光學性質

圓錐曲線的光學性質在新人教A 版選擇性必修第一冊的第113 頁的例5、第132 頁例2 以及第140 頁閱讀與思考中都有出現,是圓錐曲線的重要特性. 簡述如下:

拋物線的光學性質與對稱軸平行的光線投射到拋物線上,經反射后反射光線必通過焦點;反之, 由焦點出發的光線投射到拋物線上, 其反射光線與對稱軸平行.

圖3

橢圓的光學性質從橢圓的一個焦點出發的光線投射到橢圓上,經過反射后反射光線必通過另一個焦點.

雙曲線的光學性質從雙曲線的一個焦點出發的光線投射到雙曲線上,反射光線的延長線必通過另一個焦點.

圖4

圖5

關于圓錐曲線的光學性質的證明的文章比較多,這里不再給出,有興趣的讀者可自行查閱資料.

4. 推廣

基于圓錐曲線的光學性質及定義,我們可以將題目1 中的阿基米德三角形的這一性質推廣到橢圓和雙曲線中.

推廣1如圖6, 已知點P在橢圓外, 過點P作橢圓兩條切線, 切點分別是A、B,F1、F2是橢圓的左右焦點, 則∠PF1A= ∠PF1B,∠PF2A=∠PF2B.

圖6

證明提示如圖7, 延長F1A至M, 使得AM=AF2, 延長F1B至N, 使得BN=BF2. 根據橢圓的光學性質可知∠F2AP= ∠QAF1= ∠MAP, 易得ΔPAF2ΔPAM(SAS), 所以PF2=PM; 同理可得PF2=PN, 即PM=PN. 又F1M=F1A+AM=F1A+AF2= 2a, 同理,F1N= 2a, 即F1M=F1N, 從而可得ΔPMF1ΔPNF1(SSS),所以∠PF1A=∠PF1B.又∠PF2A= ∠PMA= ∠PNB= ∠PF2B,即∠PF2A=∠PF2B,命題得證.

圖7

推廣2如圖8, 已知點P在雙曲線外, 過點P作雙曲線某一支的兩條切線, 切點分別是A、B,F1、F2是雙曲線的左右焦點,則∠PF1A=∠PF1B,∠PF2A=∠PF2B.

圖8

證明提示如圖9,在BF1上取點D,使BD=BF2;在AF1上取點E, 使AE=AF2. 根據雙曲線的光學性質可知切線PB平分∠F1BF2,易得ΔPBD∽= ΔPBF2(SAS),所以PD=PF2; 同理可得PF2=PE. 又根據雙曲線定義可知F1D=F1B-BF2= 2a=F1A-AF2=F1E,所以ΔF1DPΔF1EP(SSS),所以∠PF1B= ∠PF1A,又由∠F1DP=∠F1EP可知∠PDB=∠PEA,而∠PDB=∠PF2B,∠PEA= ∠PF2A,即∠PF2B= ∠PF2A,命題得證.

圖9

通過以上的簡要證明,可以看出阿基米德三角形的這一性質可以通過圓錐曲線的光學性質和定義獲得,這反映了他們之間內在的聯系. 而在揭示這種聯系的過程中,我們又靈活運用了初中所學的“構造全等三角形證明等量關系”的方法,突出了幾何證明的思想和初高中數學銜接的重要性. 事實上,因為圓錐曲線的定義就是一種幾何的等量關系,故而從幾何角度理解該性質的證明是很有必要且相當有趣的.