多重視角爭奇斗艷 各類方法百花齊放
——2023 福州3 月質檢第12 題解析

福建省福清第三中學(350000) 唐 洵

2020 年新高考實施以來,以重要不等式、基本不等式為載體的試題頻繁出現,如2020 新高考Ⅰ卷第11 題、2021 年新高考Ⅰ卷第5 題、2022 新高考ⅠⅠ卷第12 題,側重考查了數學運算、邏輯推理以及數據分析的核心素養. 然而,此類問題并非僅有重要不等式、基本不等式這兩把解題利刃,本文對一道質檢試題給出了多角度、深層次的解析,旨在增加讀者分析、解決此類問題的能力.

1 題目與解答

視角一、不等式視角

視角二、參數方程視角

視角三、函數視角

視角四、圖形視角

圖1

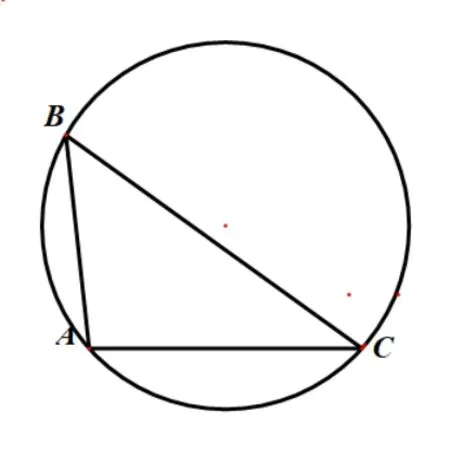
圖2

點評并非所有的代數問題都存在幾何背景,也并非所有的代數問題都適合幾何化處理,有些處理方法甚至讓人產生小題大做的感覺,此類方法(如解法十到十二)在習題教學中可以不必滲透,但作為研究必不可少.

視角五、特值視角

點評特值的選取要立于常規,一般雙變元問題往往采取固定一個,求解另一個的角度選取特值;此外基本不等式或者重要不等式中常常令x=y、x= -y選取特值;在平時適當訓練,掌握選取的套路,考試才能胸有成竹.

2 追本溯源

在求解題1 的過程中,不難發現,二次曲線x2+xy+y2=3 關于直線y=x,y= -x對稱,筆者猜想該二次曲線可能表示一個橢圓,那么猜想是否成立? 選項的設定是否存在著更深層次的幾何背景? 帶著這些疑問和困惑,為了看清問題的本質,筆者作出了進一步的思考.

考慮如下的變換

其幾何意義是將坐標軸旋轉45°,代入x2+xy+y2= 3中,得,這是一個長軸為, 短軸為的橢圓,再將坐標軸旋轉回去,得到圖形如圖3 所示. 基于上述事實,選項A、B 可以理解為直線2x+y=t1與橢圓有交點時t1的取值范圍,作出臨界狀態如圖4 所示,選項C、D 可以理解為橢圓x2-xy+y2=t2與橢圓x2+xy+y2=3 有交點時t2的取值范圍,作出臨界狀態如圖5 所示;因此本題的幾何背景為研究直線與橢圓、橢圓與橢圓的位置關系.

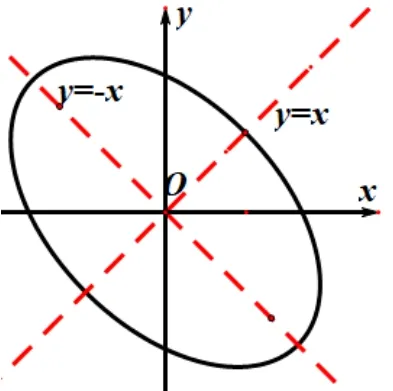
圖3

圖4

圖5

本題與2022 年新高考ⅠⅠ卷第12 題(題目2)極為相似,相比高考題而言,本題的難度略有增加,更加注重條件和結論的變形,但兩道問題的解題手法以及題目背后的幾何背景如出一轍,讀者可以自行探究題目2.

題目2(2022 年新高考ⅠⅠ卷第12 題) 若x,y滿足x2+y2-xy=1,則( )

A.x+y≤1 B.x+y≥-2

C.x2+y2≤2 D.x2+y2≥1

3 教學啟示

(1)博學主干知識, 課堂有的放矢. 教材是最好的老師,高考試題往往取之于課本,又高于課本;因此在的教學中,要注重課本與高考之間的聯系,對課本的例題、習題適當的拓展延伸,到達高考的高度;同時,教師要注重汲取多元化的知識,了解競賽、強基計劃、高等數學中與課本的交匯的相關知識,這樣才能居高臨下,輕松駕馭課堂.

(2)審問命題之道, 研究追本溯源. 所謂教而不研則淺,研而不教則空,教師必須精研高考真題,交流試題的解法,了解試題的考向,把握試題的難度,洞悉試題的背景,以便習題教學時避免南轅北轍,更快提升課堂效率.

(3)慎思新舊關聯,轉化解題思維. 新高考更加注重素養的考查,但并不意味著舊高考的一些解題手法隨風而逝;解題時應該關注新舊差異,利用新知識解題的同時,要友好對待一些“老知識”,如參數方程等,讓學生體會到解題的優越性, 適當轉化解題思維; 解答時, 不必只拘泥于單純某種視角、某種方法.

(4)明辨幾何背景,突出數形結合. 數缺形時少直觀,形少數時難入微,剖析代數問題的幾何背景有助于拓寬學生的解題視野,提升學生的解題興趣,激發學生的解題靈感,在解題時能夠站得高,看得遠,會當臨絕頂,一覽眾山小.

(5)篤行一題多解,授漁去粗取精. 教師在進行習題教學時,要立足學生的知識層面與能力范疇,精選常用解題方法,通過多角度、深層次的剖析問題,讓學生有所積累,以便其在解題時若是關上一扇門,還能打開一扇窗.