基于校正環節與改進LADRC的并網電壓控制

袁昌盛,程度煦,周雪松

(1. 中國電子科技集團公司第十六研究所,安徽 合肥 230000;2. 天津理工大學電氣電子工程學院,天津 300384)

1 引言

隨著全球經濟發展,對化石能源的需求量在不斷增加,但隨著時間推移化石能源會不斷的枯竭,而風能是用之不竭的,因此發展風力發電是一種趨勢[1-3]。在風力發電系統中并網逆變器有著廣泛的應用,但其耦合性強,易受內外擾動影響,甚至導致系統失穩,需采取相應的控制策略加以抑制。因此分析并網逆變器的控制策略,抑制擾動對電網穩定的影響,保證風電并網逆變器在多種工況下的穩定運行,對風電系統在正常條件下工作有非凡的意義。

目前用于穩定網側直流母線電壓的方法較多。各種控制策略各有優點和適用限制:主從控制策略加強直流母線電壓的穩定性,但是在技術上的設計比較困難,主要是由于網側與機側在控制系統方面相互耦合[4];下垂控制可實現有功與無功的無互聯控制,并且控制的模式較為靈便,但是較難實現電網電壓的安穩定運行[5]。文獻[6,7]應用LADRC策略對網側直流母線電壓進行了控制,提高了信號的跟蹤與抗干擾能力,但是參數添加了一倍,調參較為繁瑣,且控制器的結構較為復雜。

綜上所述,已有一些文獻利用LADRC穩定并網直流母線電壓,但都未考慮到參數眾多與結構簡便的問題。本文提出的策略是在傳統LADRC基礎上簡化,并參照超前滯后的思想將LESO中的參數改進,且將其微分環節引入總擾動支路中。通過上述的改善不但使LADRC的結構得到簡化,且很好的提高了LADRC擾動觀測能力與抗干擾性能。

2 網側逆變器的數學模型

圖1是網側逆變器結構圖,Rg為網側等效電阻,Lg為網側濾波器電感,Cg為網側濾波器電容。

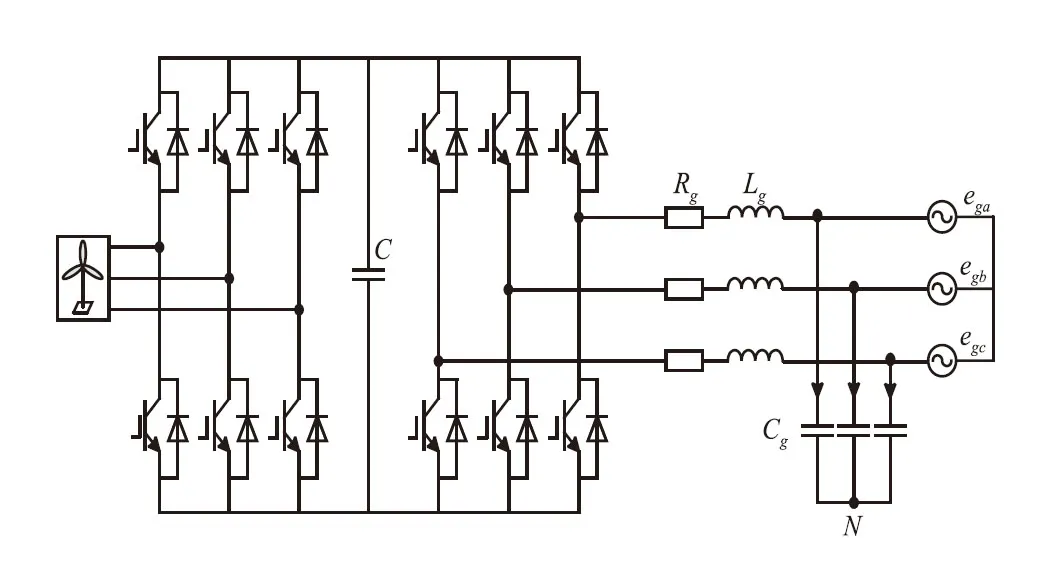
圖1 網側風電逆變器的結構圖

根據風電系統的拓撲結構,得到KVL三相電壓方程為

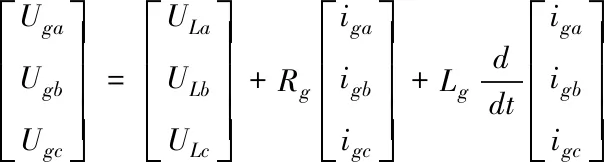
(1)

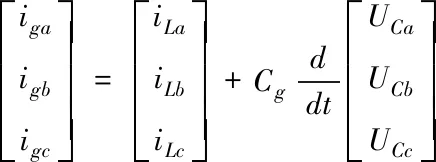
(2)

式中:Uga、Ugb、Ugc、iga、igb、igc是三相網側逆變器的電壓與電流;ULa、ULb、ULc、iLa、iLb、iLc分別為輸出電壓與電流。

經坐標變換轉換后,可知

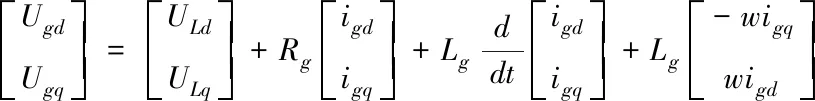
(3)

(4)

式中:Ugd、Uqd、igd、igq分別為網側逆變器電壓與電流在d、q軸上的分量;ULd、ULq、iLd、iLq分別為d、q軸上的輸出電壓分量與電流分量,w為電角速度。

對(3)式進行求導化簡,并且將(2)式代入其中可得

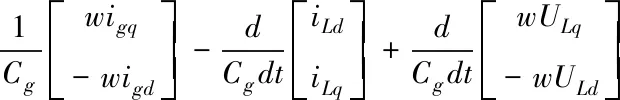
(5)

由式(5)知,風電網側逆變器是一個多變量和耦合性較強的系統,因此應用傳統控制策略不能很好達到工業要求的控制標準。

3 改進LADRC的設計

LESO是LADRC主要組成部分,由于其擾動觀測性能是LADRC發揮作用的關鍵,因此在傳統LESO的基礎上進行相應的改進。

根據文獻[8]可得傳統LESO中擾動傳遞函數

(6)

由于高階系統與二階系統在中低頻的頻率特性是類似的,故上述三階系統可以近似作為二階系統來研究。

由上式(6)三階系統可得二階系統為

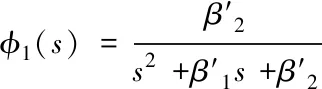
(7)

通過上式擾動觀測傳遞函數表達式分析可知,傳統的LESO在快速性與無超調上存在著矛盾,此特征表明傳統的LESO在擾動觀測方面表現的不夠優越。

由上式(7)和典型二階系統相對比可知

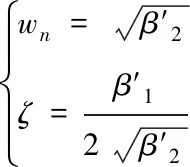
(8)

式(8)中,wn是標準二階系統中角頻率,ζ是阻尼比。

二階系統中的上升時間和超調量等因素主要取決于wn和ζ。而參數β′2的變化可同時影響wn和ζ。即β′2參數對系統動態與穩態性能作用是最大的。

本文根據上述分析對傳統LESO中的β′2進行改進,其主要是參考超前滯后的思想。

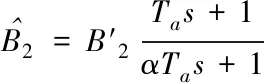
(9)

式(9)中Ta為時間常數;a是0～1中的系數,則新型LESO的擾動觀測傳遞函數為

(10)

式(7)和式(10)相比,多了一個左半平面的零點,系統的根軌跡向左偏移,加強了系統的穩態與動態特性能。

為進一步提高擾動觀測性能,在總擾動支路中引入超前滯后環節,則改進LESO擾動觀測傳遞函數為

(11)

圖2是三種LESO在Bode圖上的性能對比;綜合分析了解改進LESO觀測器帶寬得到更大程度增加,提高了擾動觀測能力顯著,且在中頻段的時候,相位滯后的現象得到解決。

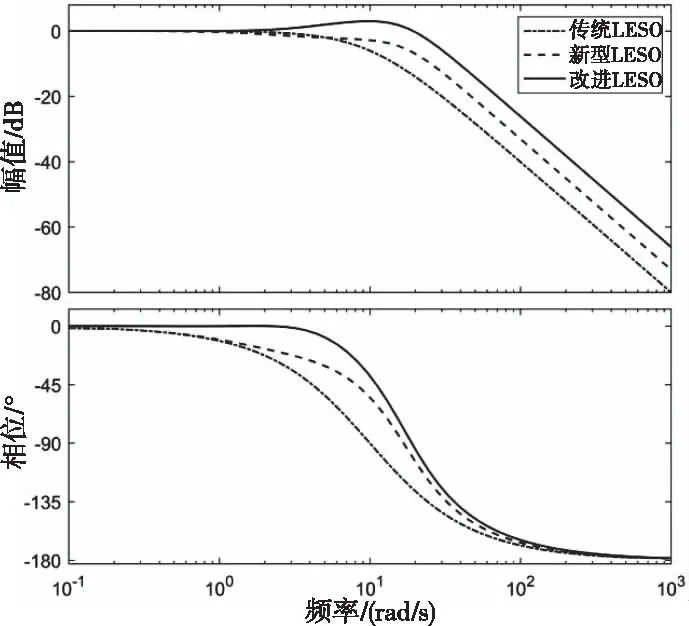
圖2 三種LESO頻域特性曲線

4 穩定性分析

針對本文所提的模型,證明其穩定性。

由文獻[9]可知LESO表達式為

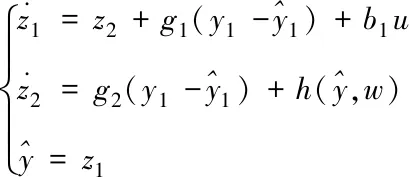
(12)

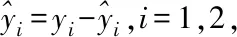
(13)

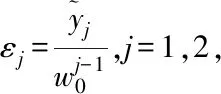
(14)

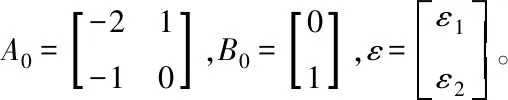
定義李雅普諾夫函數V(ε)=εTNε,則

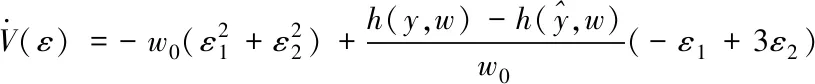
(15)

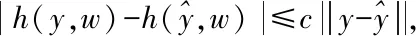
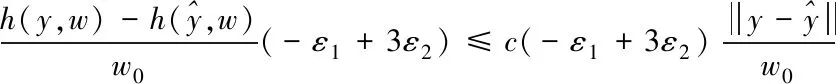
(16)

又由-ε1+3ε2=2εTNB0,式(16)可化為

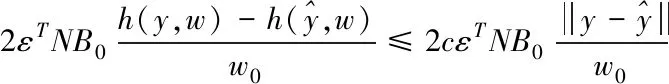
(17)

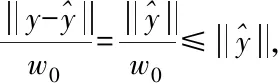
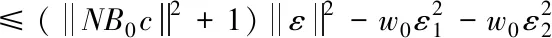
(18)

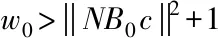
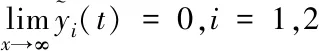
(19)

由文獻[9]可知:

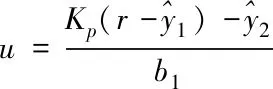
(20)

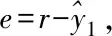
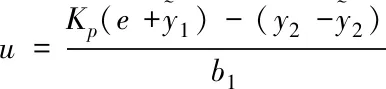
(21)

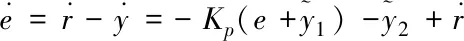
(22)

利用最值誤差的控制信號使被控對象得到激勵,可將輸出信號快速流出去。則系統變成

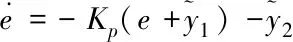
(23)

將式(23)寫成狀態空間形式為

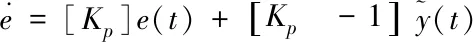
(24)

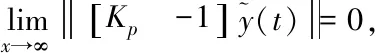
5 仿真與分析

為驗證本文所設計的控制系統的性能效果,在MATLAB/Simulink平臺上展開相關的仿真分析,1.5MW永磁風電機組控制模型如下圖3所示。在仿真分析當中,本文和文獻[10]中提出的傳統LADRC進行對比分析,利用文獻[10]的參數進行仿真驗證。

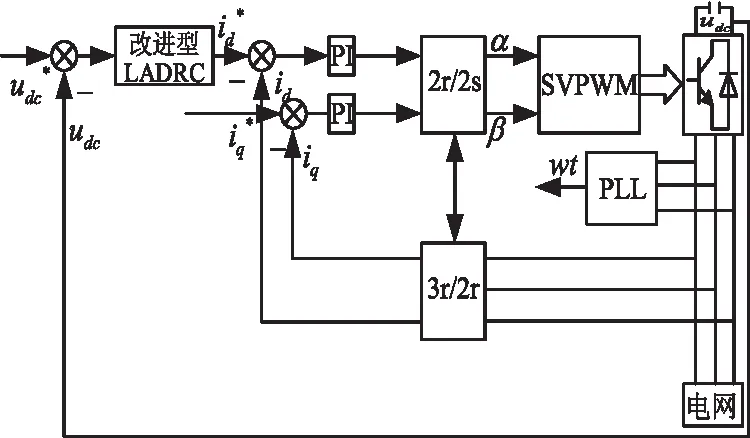
圖3 改進型LADRC控制仿真圖

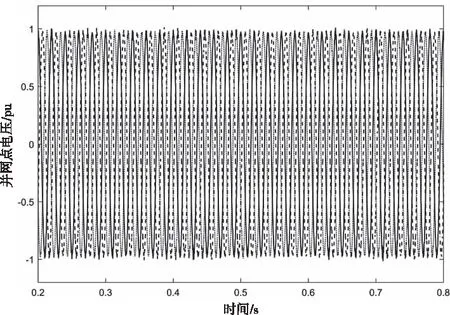
圖4 對稱工況下的并網電壓波形

圖5 不對稱工況下的并網電壓波形

選用的并網逆變器與控制器參數分別為:PN=1.5MW,U網側線電壓=690V,U直流母線電壓=1070V,C=240μF,L=20μH,R=0.942Ω;wc=2500rad/s,w0=700rad/s,b0=12000。

1) 設置工況開始時間為1.0s,結束時間為1.2s;則加載60%工況下的直流母線電壓如圖6所示。

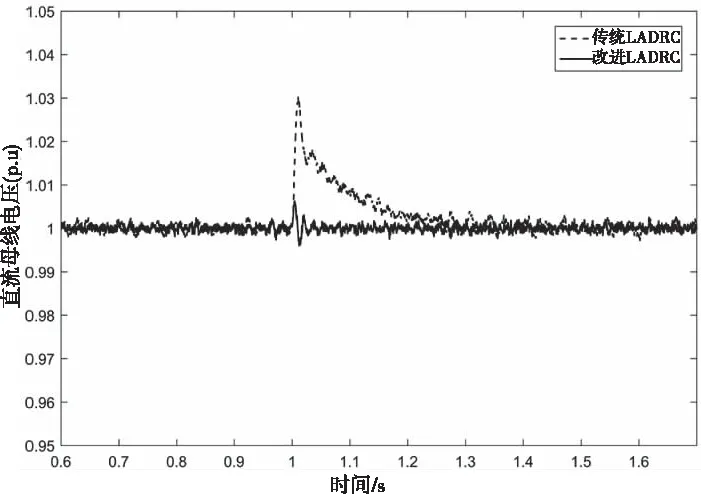
圖6 加載60%工況下的直流母線電壓

2) 設置工況開始時間為1.0s,結束時間為1.2s;則減載60%工況下的直流母線電壓如圖7所示。

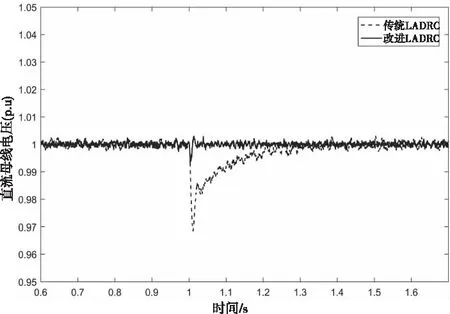
圖7 減載60%工況下的直流母線電壓

3) 設置工況開始時間為0.6s,結束時間為0.8s;則對稱跌落40%工況下的直流母線電壓如圖8所示。

圖8 對稱跌落40%工況下的直流母線電壓

4) 設置工況開始時間為0.6s,結束時間為0.8s;則不對稱跌落40%工況下的直流母線電壓如圖9所示。

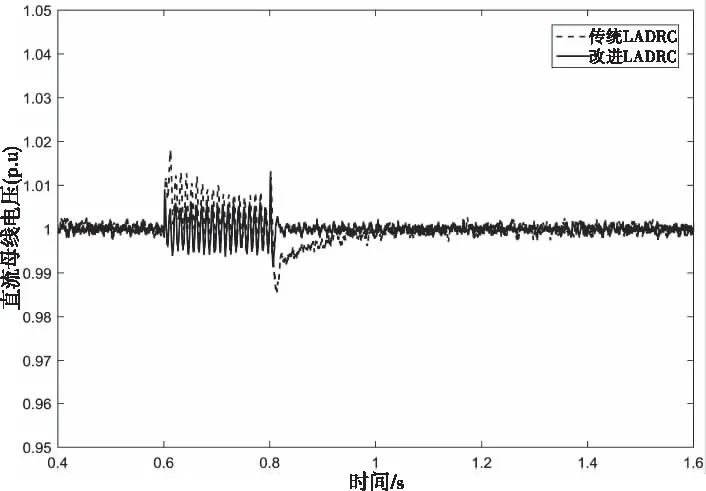
圖9 不對稱跌落40%工況下的直流母線電壓

圖6與圖7分別是加載和減載工況下的直流母線電壓波形,傳統LADRC加載工況下超調量為0.03pu,改進LADRC超調量為0.01pu;在減載工況下傳統LADRC的超調量為0.03pu,改進LADRC的超調量為0.01pu。圖8與圖9分別是對稱與不對稱跌落40%下的直流母線電壓,在對稱跌落工況下傳統LADRC超調量為0.022pu,改進LADRC超調量為0.008pu;在不對稱跌落工況下傳統LADRC超調量為0.015pu,改進LADRC超調量為0.001pu。通過上述多種工況結果對比分析可知,改進LADRC具有可行性和先進性。

6 結論

本文針對風電并網逆變器輸出的直流母線電壓穩定性易受外部干擾的問題,設計了超前滯后的微分環節與傳統LADRC相結合的改進型LADRC,最后通過理論與仿真對改進型LADRC控制策略展開分析。其得出的結果如下:①改進的LADRC有更好的抗擾與穩定性能;②由于實驗條件有限,沒有進行實物仿真,僅在仿真軟件上進行驗證,可能在細節上出現些許誤差。