基于包絡約束的幅相聯合凈空測量方法

鄧佳欣,馬丁峰,徐云山

(1. 中國飛行試驗研究院,陜西 西安 710089;2. 中國人民解放軍95966部隊,黑龍江 哈爾濱 150060)

1 引言

由于國家十四五期間大力倡導低碳能源政策,因此大量用戶會進一步加大新能源(風能和光伏發電)的投入力度,并結合微電網綜合管理系統在用電的高峰和低谷期盡可能與傳統能源行業協同工作,為低碳環保做出貢獻。其中風力發電機由于其峰值發電功率的不斷提升,其風機的規模會越來越大,塔筒和葉片均達到了近百米量級,因此相應的也存在了運行過程當中的潛在風險。根據用戶對大型風力發電機機組運行過程中的安全監控需求,需要高精度監測葉片在高速旋轉過程中與風機塔筒之間的水平距離,評估葉片掃塔概率,在發生緊急狀況之前給后臺提供預警信息,以防安全事故的發生。

為了得到葉片在風機坐標系下的實時三維坐標,需要采用雷達監控設備獲取目標的三坐標信息,從而精確測量目標的徑向距離、方位角、俯仰角信息。文獻[1]介紹了三坐標雷達系統的發展歷程,其相對于兩坐標雷達,具有更強的目標觀測能力。文獻[2,3]分別介紹了俄羅斯和荷蘭比較成熟的三坐標雷達系統,并對其雷達性能進行了全面的分析。文獻[4-10]分別從三坐標雷達系統設計、掃描體制、多維跟蹤以及目標連續觀測的高度閃爍等層面提供了不同的解決方案,為三坐標雷達的檢測、跟蹤及測高等提供了技術途徑,為后續的雷達系統提供了大量借鑒思路。

對于風力發電機的葉片凈空測量系統,由于葉片下半段與塔筒之間的凈空測量受方位維測量的影響較小,其測量誤差對于70-100米葉片的精度損失在0.2米量級,因此可以借助分時和波束技術實現方位維測量的粗估計[11,12]。然而俯仰方向的角度測量精度對葉片凈空的估計精度影響非常大,對于70-100米葉片的凈空估計精度,1度對應的估計偏差達到了1米量級,因此必須對俯仰向進行高精度測角。文獻[13-16]從多個角度提供了干涉測角的測量方法。文獻[13]從雷達干涉儀的測量誤差、基線影響、測角模糊以及測量精度等多個角度對干涉儀雷達系統進行了比較全面的分析。文獻[14]提出了一種可以應用于可全方位同時探測的米波雷達天線及相應的測角算法,天線尺寸小、結構簡單。文獻[15]提出了一種新的干涉測角數據處理算法,該算法對相位干涉儀測角中因相位解模糊出錯產生的錯誤角度值進行野值剔除,并引入2階修正卡爾曼濾波器對剔除野值之后的角度信息進行平滑修正,保證了穩定跟蹤的連續性。文獻[16]提出了一種利用空間譜估計對干涉測角系統進行解算的方法,該方法在多重信號分類(MUSIC)算法的基礎上,對協方差矩陣的估計、特征值分解、譜峰搜索等計算量較大的步驟進行了改進,提高了運算速度以及解模糊的正確率,但上述方法對系統的通道自由度和一致性要求較高。文獻[17]針對多基線相位干涉儀的相位模糊問題,提出了一種基于參差基線解模糊算法原理的改進解模糊算法,該算法具有計算量小、實時計算以及正確概率高的優點。

本文在充分借鑒上述文獻思想的基礎上,從風機葉片凈空估計的實際應用背景出發,充分考慮工程可實現性、空間約束、穩定性以及運算復雜度幾個方面,在雙接收通道雷達觀測的條件下提出了基于邊緣約束的幅相聯合約束葉片凈空測量方法。本文的結構如下:第二節簡單介紹了連續波雷達的信息體制以及風機葉片觀測的物理模型;第三節則主要介紹了所提方法的主要思想;第四節描述了算法實現的具體步驟;第五節通過連續波雷達實際采集的葉片觀測數據驗證所提方法在有多徑擾動和震動引起的雜波環境擾動下的葉片識別及凈空估計效果;最后一節總結了本文所提方法的優勢及其工程價值。

2 信號模型

由于觀測場景覆蓋范圍較小,且對于雷達系統的成本控制嚴格,因此葉片凈空測量系統采用了線性調頻連續波雷達。利用線性調頻連續波的解線頻調技術能夠大幅降低接收系統的帶寬,以較低的采樣率錄取回波數據,同時由于采用了連續波體制,雷達峰值功率可以大幅降低。雷達的發射信號波形如下所示

s(t,tm)=a(t)e(j2πfct+jπγt2)

(1)

其中t和tm分別代表雷達系統的全時間和慢時間,a(t)為發射信號的包絡,一般在發射信號帶寬內,該包絡引起的幅度變化不會超過3dB,可以忽略不計。fc為雷達系統的中心頻率,γ為線性調頻信號的調頻率。

對于風機的葉片凈空測量,采用如圖1所示的地面雷達測量方式。其中以葉片機艙平面與塔筒軸線分別為Y0軸和Z0軸,并根據右手原則確定初始坐標系的X0軸。而地面雷達的坐標系對應的坐標系分別為X1軸、Y1軸和Z1軸,兩個坐標系之間的關系由現場的實際安裝環境決定。

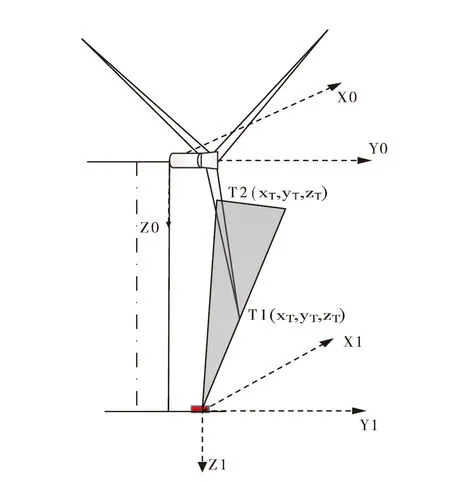
圖1 風機葉片凈空測量場景示意圖

T1和T2分別為雷達波束范圍內照射到的葉片最近端和最遠端,其相對于雷達的距離分別為R1和R2。假定雷達發射的信號帶寬為B,考慮到距離向加窗的影響,其距離向分辨率ρr為

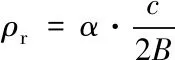
(2)

其中c為電磁波的傳播速度,α為加窗擴展系數。則葉片沿著雷達徑向方向按照距離分辨率可以劃分成如下離散的散射點集

Ri=Ri+(i-1)ρr,i∈[1,2,…,L]

(3)

其中

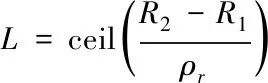
(4)

ceil()為向上取整函數。對葉片的回波進行解線頻調處理之后,其回波形式如下所示

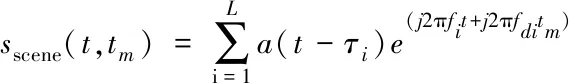
(5)

其中

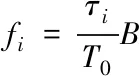
(6)

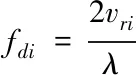
(7)

τi=2Ri/c為葉片散射點的回波延時,vri為葉片散射點相對于雷達的徑向速度。

由于場景中除了葉片自身的回波,還包括從天線旁瓣進入的地雜波、塔筒回波以及葉片和塔筒多徑等回波。其中塔筒和地雜波回波由于位于零多普勒通道,因此對檢測影響較小,但是其距離多普勒兩維積分旁瓣分量和多徑回波對目標的檢測造成了比較強的干擾,因此需要對其進行檢測剔除。雷達的總回波形式如下

stotal(t,tm)=sscene(t,tm)+sclu(t,tm)+snoise(t,tm)

(8)

3 所提方法的實現方法

根據大量實測數據的分析以及系統脈內/脈沖間的相位起伏,雜波和噪聲的分布具有隨機分布特征,由于噪聲是高斯獨立分布的,無法通過濾波器進行濾除,因此對于目標檢測而言,系統必須保證信噪比。其次,旁瓣積分雜波和多徑效應在距離、方位以及多通道間的相位也會具有比較大的隨機性。

另外,葉片的回波能量是由葉片散射點集的回波組成,其整體結構呈現近似線性的變化趨勢,在一個相干積累時間之內,每一個距離分辨單位內的散射點多普勒擴展隨著與雷達之間的距離呈現逐漸變大的趨勢,同時,結合目標葉片散射點集與兩個通道之間的固定相位差,可以利用目標在距離、速度和通道干涉相位圖的包絡約束特性對葉片進行檢測,同時剔除噪聲和雜波虛警點。

假設連續波雷達系統采用雙通道干涉相位體制,在相干積累時間內共發射了M組脈沖信號,感興趣距離門總數為L。對解線頻調之后的接收信號進行兩維FFT處理得到距離和多普勒兩維積累之后的回波。第l個距離單元、第m個脈沖、第n個通道信號兩維積累的處理如下

xn,m,l=FFTazi(FFTrange(stotal·ωrange)·ωazi)

(9)

其中FFTrange和FFTazi分別是對目標沿著距離和方位分別進行FFT處理,ωrange和ωazi是距離和方位的窗函數,再得到上述距離和方位積累回波之后,可以計算兩個通道之間的干涉相位,其處理方式如下

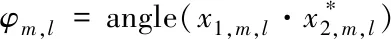
(10)

結合目標在距離、速度平面以及干涉相位平面的包絡約束特征,通過圖像計算函數分別對距離多普勒圖和干涉相位圖進行包絡檢測,并計算其交集部分,處理過程如下

clu1=cluster(x1.m,1)

clu2=cluster(φm,l)

(11)

clu=clu1∩clu2

(12)

得到目標的置信區間clu之后,對每一個距離門內檢測到的多個數據進行單元平均,進一步通過非相干積累提升信雜噪比,其距離門和干涉相位信息如下

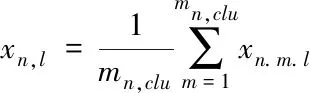
(13)

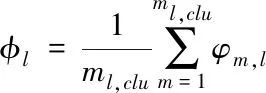
(14)

由于葉片的近似線性分布,并結合其與雷達之間的幾何分布模型,可以對多個連續距離的干涉相位信息進行二階擬合處理,其操作如下

α=polyfit(φl)

(15)

φpoly=polyval(Ri,α),i=1,2,…,L

(16)

在得到擬合干涉相位之后,可以根據兩個通道之間與葉片仰角之間的相位關系反算得到目標葉片不同散射點集相對于雷達的仰角,其換算公式如下

(17)

其中d為兩個通道之間的陣元中心間距,λ為發射信號的波長,asin()為反余弦函數。結合仰角、距離以及雷達與塔筒之間的幾何關系,可以進一步得到葉片與塔筒間的凈空值,算法的整個流程圖如圖2所示。

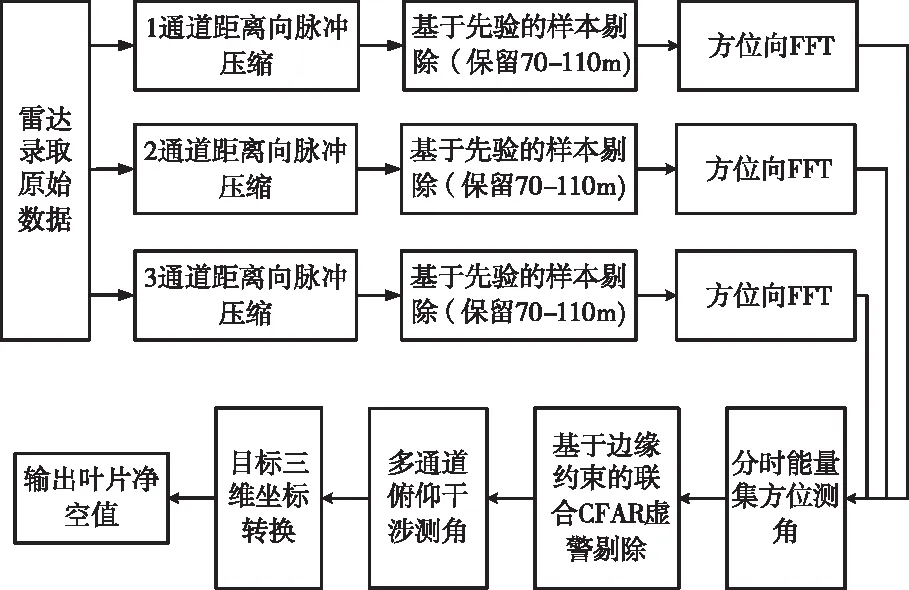
圖2 基于邊緣約束的幅相聯合葉片凈空測量流程圖

4 仿真研究

為了充分驗證所提方法的實際應用效果,利用某研究所開發的毫米波凈空監測雷達在風力發電廠的地面端進行了實際測量實驗,錄取不同風況、不同朝向的數據,其現場測試環境如圖3、圖4所示。

圖3 風電現場實際測量環境

圖4 測量過程中風機的實時轉速

錄取的實際測量數據涵蓋了從2r/min到12r/min的數據樣本,并且因風速的實時變化,風機在測量過程中出現了不同的朝向,其場景會出現一定程度的變化,剛好為驗證本文所提方法的穩定性提供了數據多樣性。因此,這組實測數據可以較好的驗證所提方法的性能。

圖5給出了風機處于10r/min情況下錄取的實測數據距離多普勒兩維分布情況。其中圖5(a)是回波的能量分布圖,圖5(b)是回波的兩通道干涉相位圖。如果對上圖的結果直接進行檢測處理,除了能檢測到葉片的目標,還能夠檢測到很多擴展的雜波以及強噪聲點。如果將上述所有檢測點共同應用于葉片與塔筒之間的距離評估,會導致系統的測量誤差增加,其目標序列對應的凈空估計結果如表1中所示,出現了凈空的跳變現象,不符合葉片凈空的連續性現象。

表1 不同目標點相對于塔筒的距離測量值

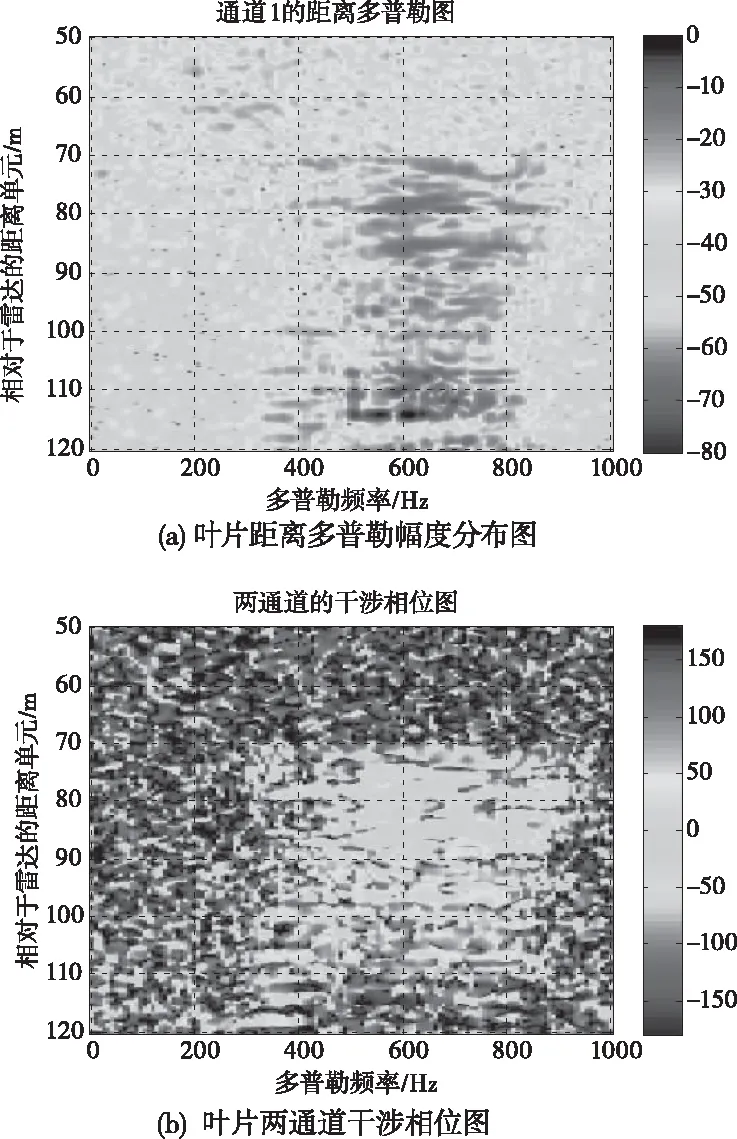
圖5 葉片距離多普勒幅度分布圖

然而,從上圖中可以看出葉片回波的幅度和干涉相位均存在比較明顯的集中現象,因此可以基于上述先驗信息,利用基于圖像能量閾值的邊緣約束方法提取葉片的邊緣輪廓。另外,由于塔筒與葉片之間存在鏡面/非鏡面的多徑效應,因此在目標的能量和干涉分布集中區域出現了干涉相位跳變的現象,這是由于多徑目標的空間觀測仰角發生了變化,使得干涉相位發生了變化,因此可以在邊緣約束的基礎上,利用幅相二維聯合檢測的方法,對邊緣輪廓內的目標進行二次剔除,從而提升葉片目標的識別精度,為提取葉片的凈空信息提供保障。

圖6給出了利用能量閾值控制和邊緣檢測的結果,從圖6(b)的干涉相位圖掩膜可以明顯發現,能夠有效提取葉片觀測仰角一直的區域,且隨著距離的變化呈現連續性變化趨勢。圖7在上述檢測結果的基礎上應用最小二乘擬合和檢測點單元非相干疊加技術,在提升葉片目標干涉相位估計精度的同時,得到了葉片相對于塔筒邊緣的凈空值。由圖7(a)可以發現,由于在邊緣約束范圍內,無法剔除所有的非葉片目標雜波點,因此需要利用最小二程擬合技術對上述結果進行平滑處理,從而保證系統的穩定度。圖7(b)給出了考慮塔筒模型和雷達間幾何關系的轉換后凈空測量值,與激光測量儀的實際結果相差≤0.5m,測量結果完全符合工業應用要求。詳細的凈空點測量信息如表1所示,通過對比發現,采用本文所提的方法能夠顯著改善因雜波和強噪聲環境引起的凈空估計跳變問題,并且提升凈空的估計精度。因此,本文所提算法相比常規的檢測和干涉相位測角技術,具有更有的穩定性和測量精度,提升系統針對風機復雜工作場景下的干擾點剔除能力。另外,本文所提方法的計算復雜度較低,運算量增加可以忽略不計,因此其帶來的系統增效在大多數應用場景下具備實際的工程價值。

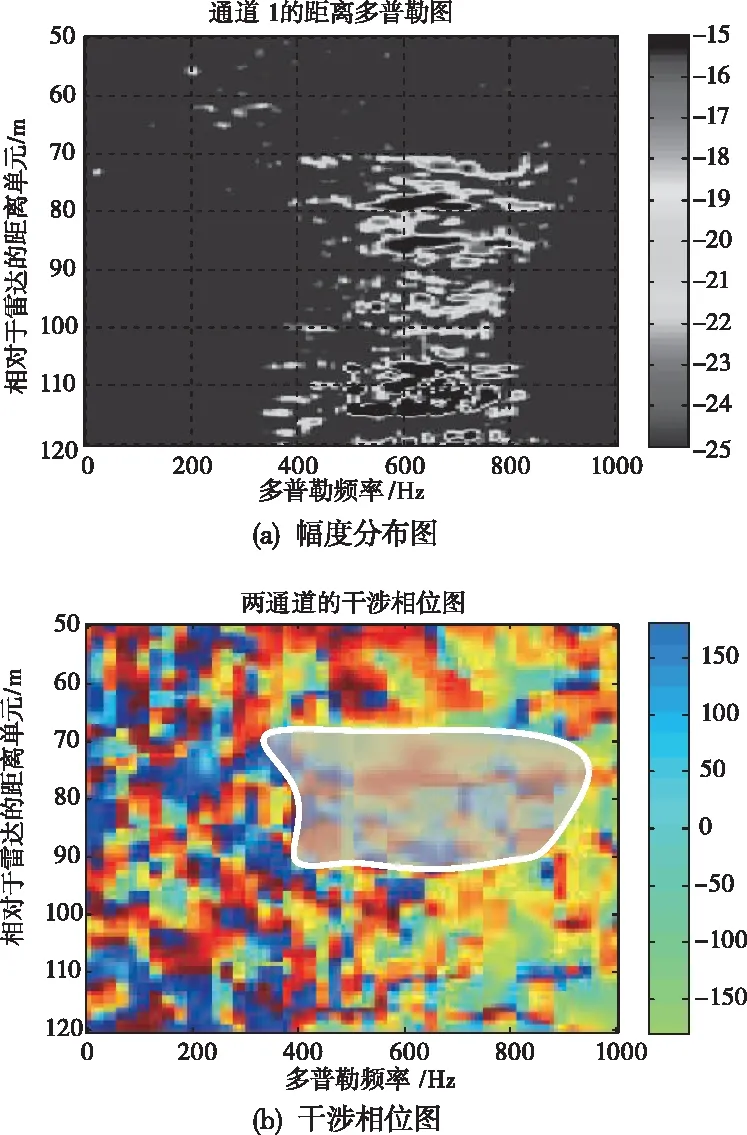
圖6 基于邊緣約束的距離多普勒幅度分布與兩通道干涉相位圖

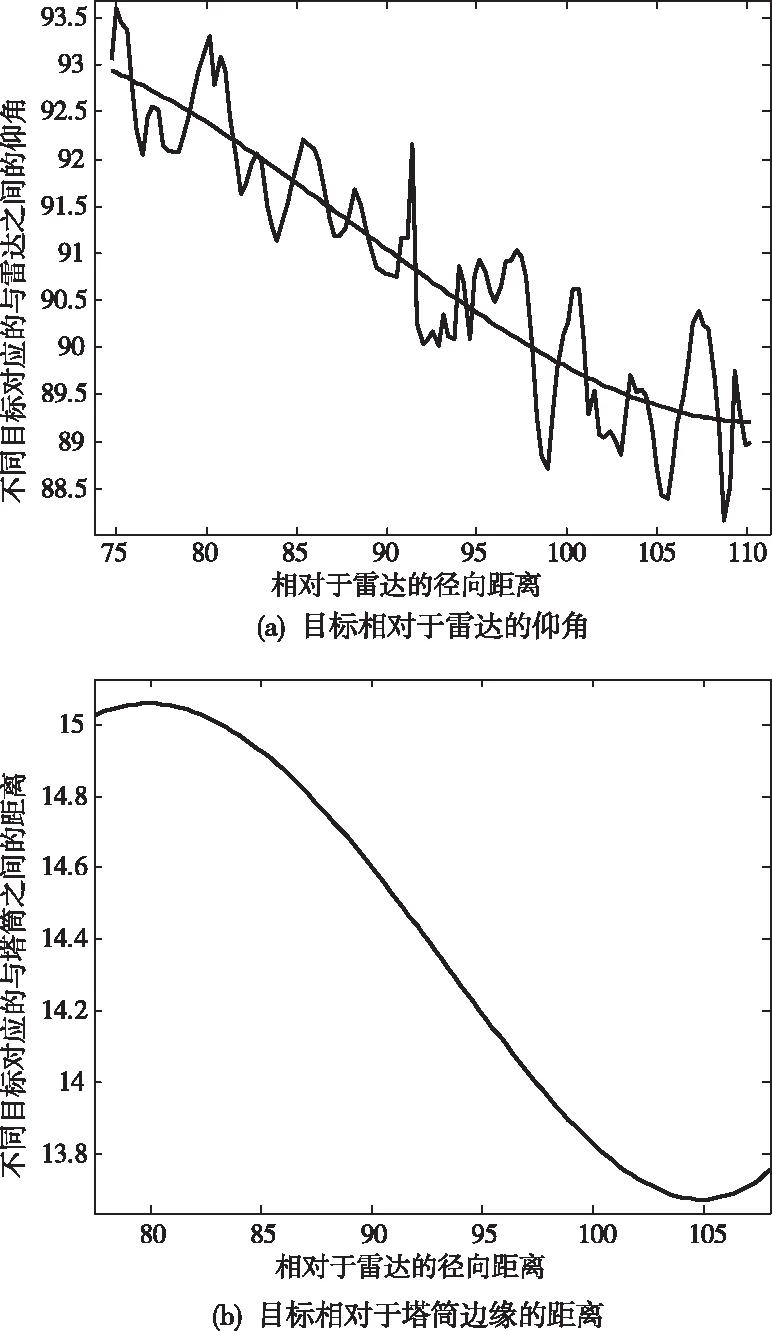
圖7 基于邊緣約束的葉片凈空測量值

5 結論

本文所提方法提供了一種應用于地面安裝雷達測量風機葉片相對于塔筒凈空的測量方法,能夠有效克服葉片與塔筒多次彈射和塔筒晃動引起的雜波擴散及虛警檢測問題。該方法基于葉片的整體先驗信息以及圖像能量閾值邊界約束方法,聯合目標的距離多普勒幅相二維分布圖,應用掩膜檢測的方法能夠盡可能剔除非葉片的雜波信息,同時利用葉片的近似線性的變化特性,能夠進一步剔除虛警點,最終利用最小二乘擬合和單元平均提升目標的相位估計精度,從而保證了葉片的凈空估計連續性和準確性。所提算法能夠在葉片高速旋轉過程中塔筒震動導致的雜波擴散分布圖中有效的識別出葉片分量,同時借助幅相二維檢測圖,能夠改善在強雜波和噪聲環境中的檢測性能,適用于自適應葉片目標的選擇與參數估計;另外所提方法應用的圖像閾值約束和二維掩膜測量運算量極低,能夠顯著降低系統的運算復雜度,對于葉片實時監測系統的低成本化具有非常大的工程意義。