“超幾何分布”教學設計

何春強

摘? 要：通過不放回摸球試驗，利用建立二項分布模型積累的數學活動經驗，帶領學生經歷抽象試驗特征、推導分布列、直觀猜想并計算、驗證超幾何分布隨機變量均值的過程，引導學生辨析二項分布與超幾何分布的聯系與區別，幫助學生積累建立概率模型的經驗，體會概率的決策作用.

關鍵詞：不放回抽樣；超幾何分布；區別與聯系

一、教學內容解析

“超幾何分布”是人教A版《普通高中教科書·數學》選擇性必修第三冊（以下統稱“教材”）第七章第4節“二項分布與超幾何分布”第2課時的內容.“超幾何分布”是統計學中的一種離散型隨機變量的概率分布，與二項分布一樣，都是描述從有限（[N]）個物品（其中包含[M]個指定種類的物件）中抽出[n]個物品，成功抽出該指定種類物品次數的概率分布情況. 不同的是，二項分布采用有放回抽樣，超幾何分布采用不放回抽樣. 因其概率形式與超幾何函數的級數展開式的系數有關，故稱為超幾何分布.

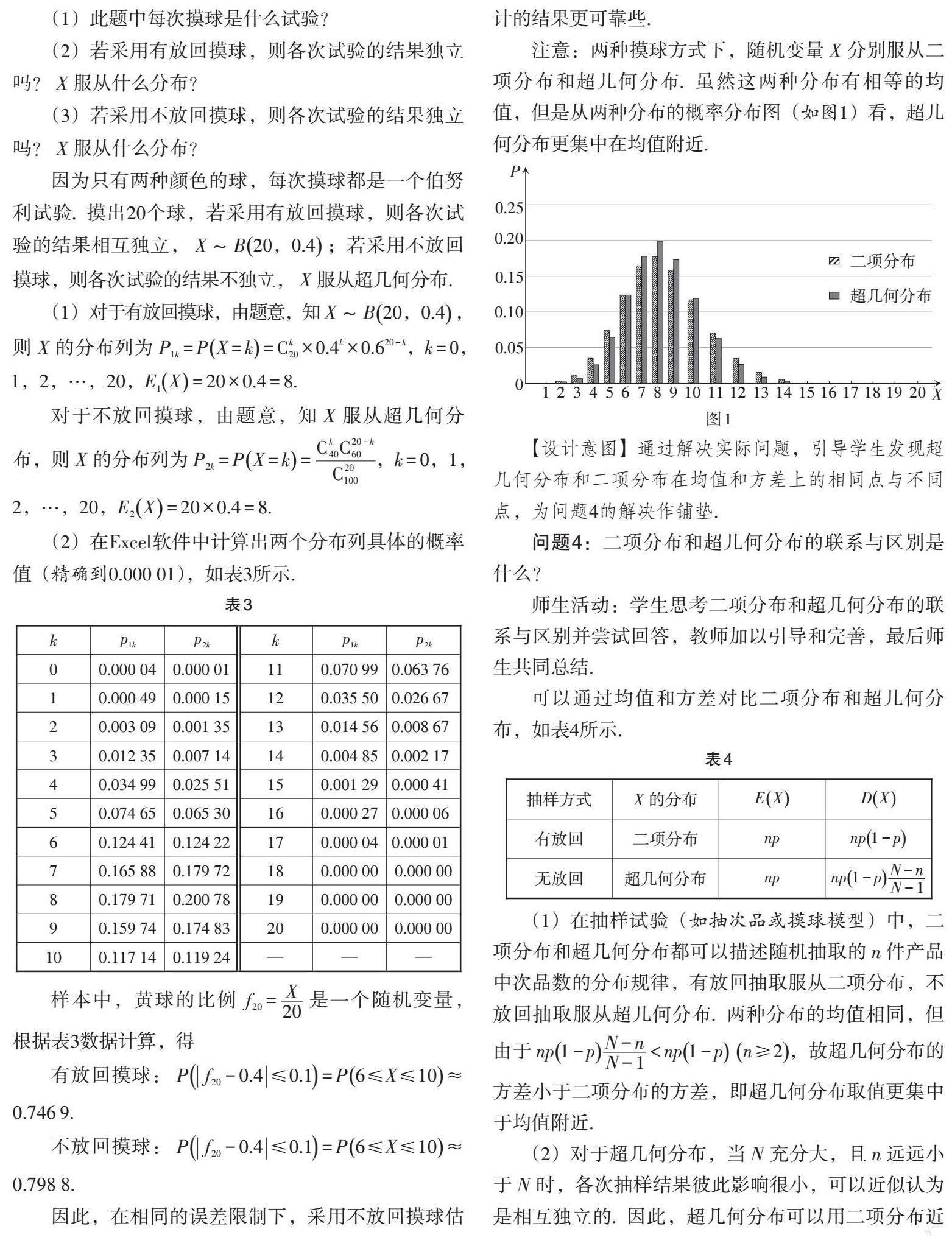
超幾何分布與二項分布都是特殊的離散型隨機變量的分布，在日常生活中大量存在，它們有著相同的數學期望，但抽取方式不同，超幾何分布更集中在均值附近. 但是當[n]遠遠小于[N]時，每抽取一次后，放回與不放回對[N]的影響都很小，此時，超幾何分布與二項分布近似.

“超幾何分布”一課內容的學習安排在一般離散型隨機變量及其分布列之后，緊接二項分布，通過具體實例，引導學生感受放回抽樣與不放回抽樣的聯系與區別，這種從一般到特殊、從抽象到具象的辨析對比，關注了學生的數學抽象和邏輯推理素養，同時實現了對本章知識的深度理解和完美總結.

二、教學目標設置

通過對比放回抽樣和不放回抽樣，說明超幾何分布的特征，能求超幾何分布的分布列和均值，發展學生的數學建模和數學抽象素養；能用自己的語言解釋二項分布和超幾何分布的聯系與區別，并能夠選擇正確的模型解決實際問題，發展學生的數學建模素養.

教學重點：超幾何分布的概念，超幾何分布的分布列和均值.

教學難點：在實際問題中抽象出模型的特征；超幾何分布期望的推導及區分二項分布和超幾何分布.

三、學生學情分析

學生在學習本節內容之前，已經完整地學習了一般離散型隨機變量及其分布列的內容，明確了研究離散型隨機變量及其分布列的一般方法. 同時，通過對二項分布的學習，學生對有放回摸球試驗已經非常熟悉，這些都有利于我們進行不放回摸球試驗的教學. 但是超幾何分布的概率依托于古典概型，要借助組合數進行計算，特別是對超幾何分布的數字特征進行研究時，公式推理比較復雜，計算量也比較大. 另外，在對二項分布和超幾何分布進行對比分析時，要求學生具有較強的數學建模和數學抽象的能力. 對此，通過設置有趣的情境案例，借助PPT、Excel等軟件激發學生的學習興趣，提升數學運算效率，讓學生直觀感受二項分布和超幾何分布的聯系與區別.

四、教學策略分析

為了便于教學的順利切入和展開，本節課從一個有趣的生活案例引入，通過對有放回和不放回兩種抽獎方式的對比分析，在學生作決策的過程中自然地提出超幾何分布的概念，并在此基礎上引導學生猜想、推理、論證超幾何分布的均值. 再通過一個數據較大的摸球模型，借助Excel軟件的計算功能，讓學生感受超幾何分布和二項分布的聯系與區別. 通過從特殊到一般再到特殊的層層推進，設計問題串教學，以問題的提出與解決為主線，始終在學生思維的最近發展區設問，通過不斷探究、發現，在師生互動、生生互動中完成超幾何分布的探究與學習. 有效化解教學的重點和難點.

本節課采取啟發式教學和合作探究相結合的教學策略，充分調動學生探究的積極性，使每名學生都能經歷數學模型的抽象過程，為不同認知的學生提供學習的機會和幫助.

五、教學過程設計

環節1：實例引入，提出問題.

問題1：購物節即將來臨，某商家擬推出一項抽獎活動：在一個不透明的盒子里放有外觀相同的10個乒乓球，其中有3個乒乓球的表面上寫有“獎”字，顧客消費滿500元便可獲得兩次抽獎機會，每次從盒中任意摸取一個球，抽中帶有“獎”字的乒乓球，可以獲得50元代金券. 現有兩種抽獎方式可供選擇——有放回抽獎和不放回抽獎，試利用所學數學知識，作出合理的決策方案.

師生活動：每組學生分成兩個小組，分別進行有放回抽獎和不放回抽獎兩種方案有關數據的計算，然后再進行小組討論，作出合理的決策方案. 教師適時進行指導.

記中獎的次數為[X]，獎金為[Y]元，則[Y=50X].

事實上，若采用有放回抽獎，每次中獎的概率均為0.3，且各次抽取的結果相互獨立，此時[X]服從二項分布，即[X?B2，0.3，EX=2×0.3=0.6，EY=][50EX=30]，[DX=2×0.3×0.7=0.42].

若采用不放回抽獎，則每次抽取時條件不同，且各次抽取的結果不獨立，不滿足[n]重伯努利試驗的特征，此時[X]不服從二項分布，只能根據古典概型求[X]的分布列. 而在不放回抽獎過程中，逐個不放回抽取2個乒乓球和一次性抽取2個乒乓球結果相同，故可以用如下方法求[X]的分布列.

從10個乒乓球中任取2個共有[C210]種不同的取法，中獎個數[X]的可能取值為0，1，2，恰有[k]個中獎的取法有[Ck3C2-k7]種.

因為兩種抽獎方式獲得代金券的數學期望值都是30，但不放回抽獎的方差更小，所以選擇不放回抽獎方式.

【設計意圖】通過具體的問題情境，激發學生的學習興趣. 學生積極思考并參與互動，表達自己的見解，教師借機引入超幾何分布的概念.

環節2：抽象概念，辨析內涵.

問題2：問題1中不放回抽獎方式不服從二項分布，你能說說這類不放回簡單隨機抽樣的特征嗎？你能根據這些特征嘗試歸納出這一類分布的概念嗎？

追問1：公式[PX=k=CkMCn-kN-MCnN]中各個字母的含義是什么？

追問2：公式[PX=k=CkMCn-kN-MCnN]中有關字母的取值范圍是什么？

師生活動：學生觀察、比較問題1中的有放回抽樣和不放回抽樣，歸納出超幾何分布模型的特征，教師進行總結.

一般地，假設一批產品共有[N]件，其中有[M]件次品. 從[N]件產品中隨機抽取[n]件（不放回），用[X]表示抽取的[n]件產品中的次品數，則[X]的分布列為[PX=k=]

其中，[N]表示總體中的個體總數，[M]表示總體中的特殊個體總數（如次品總數），[n]表示樣本容量，[k]表示樣本中的特殊個體數（如次品數）.

【設計意圖】通過比較有放回抽樣和不放回抽樣，歸納出超幾何分布模型的特征，由特殊到一般地得出超幾何分布的分布列，加深學生的理解和思考.

例1? 一批零件共有30個，其中有3個不合格，隨機抽取10個零件進行檢測，求至少有1件不合格的概率.

師生活動：教師引導學生思考零件中不合格品的個數服從什么分布. 若服從超幾何分布，則公式中的[N，M，n，k]在此題中各是多少？學生基于思考給出以下解題過程.

在學生完成解題后，引導學生發現還可以通過[PX≥1=1-PX=0]求解. 并再次強調超幾何分布的模型是不放回抽樣，在超幾何分布中，只需要確定參數[N，M，n]的值就可以根據公式求出[X]取不同值時的概率.

【設計意圖】通過該例的分析與解答，促進學生進一步理解超幾何分布的概念及其特點，發展學生的邏輯推理、直觀想象、數學抽象和數學運算素養.

問題3：根據已有經驗，在定義了超幾何分布的概念后，要研究什么？

追問：你能推導出服從超幾何分布的隨機變量的均值嗎？

師生活動：學生獨立探究，然后展示、交流，教師予以引導、完善，最后師生共同總結.

超幾何分布的方差計算比較復雜，不作要求，感興趣的學生可以嘗試推導：[DX=np1-pN-nN-1].

【設計意圖】通過探究服從超幾何分布的隨機變量的均值，加深學生對超幾何分布的認知，同時發展學生的邏輯推理能力.

環節3：例題練習，鞏固理解.

例2一個袋子中有100個大小相同的小球，其中有40個黃球，60個白球，從中隨機摸出20個球作為樣本. 用[X]表示樣本中黃球的個數.

（1）分別就有放回摸球和不放回摸球，求[X]的分布列及其數學期望；

（2）分別就有放回摸球和不放回摸球，用樣本中黃球的比例估計總體中黃球的比例，求誤差的絕對值不超過0.1的概率.

師生活動：教師引導學生思考以下問題.

（1）此題中每次摸球是什么試驗？

（2）若采用有放回摸球，則各次試驗的結果獨立嗎？[X]服從什么分布？

（3）若采用不放回摸球，則各次試驗的結果獨立嗎？[X]服從什么分布？

因為只有兩種顏色的球，每次摸球都是一個伯努利試驗. 摸出20個球，若采用有放回摸球，則各次試驗的結果相互獨立，[X]～[B20，0.4]；若采用不放回摸球，則各次試驗的結果不獨立，[X]服從超幾何分布.

（1）在抽樣試驗（如抽次品或摸球模型）中，二項分布和超幾何分布都可以描述隨機抽取的[n]件產品中次品數的分布規律，有放回抽取服從二項分布，不放回抽取服從超幾何分布. 兩種分布的均值相同，但由于[np1-pN-nN-1

（2）對于超幾何分布，當[N]充分大，且[n]遠遠小于[N]時，各次抽樣結果彼此影響很小，可以近似認為是相互獨立的. 因此，超幾何分布可以用二項分布近似. 從方差角度看，由于[N-nN-1≈1]，故兩個分布的方差也近似相等.

（3）在確定分布列時，超幾何分布必須同時知道[N]和[M]的值，而二項分布只需要知道[p=MN]即可.

【設計意圖】通過問題辨析，深化學生對超幾何分布的理解，明確二項分布和超幾何分布的聯系與區別，發展學生的邏輯推理、直觀想象、數學抽象和數學運算素養.

環節4：小結提升，形成結果.

問題5：回顧本節課所學內容，并回答下列問題.

（1）超幾何分布的分布列是怎樣的？

（2）超幾何分布的均值是多少？

（3）在抽樣試驗（如抽次品或摸球模型）中，如何區分二項分布和超幾何分布？

師生活動：學生嘗試獨立解決，其他學生進行補充，最后師生共同總結.

【設計意圖】通過對問題的深入思考，加深學生對超幾何分布的理解與認知，使他們更加深刻地體會二項分布和超幾何分布的聯系與區別.

環節5：目標檢測，檢驗效果.

1. 下列隨機事件中的隨機變量[X]服從超幾何分布的是（? ? ）.

（A）將一枚硬幣連拋3次，正面向上的次數[X]

（B）從7名男生與3名女生共10名學生干部中選出5名優秀學生干部，選出女生的人數[X]

（C）某射手射擊的命中率為0.8，現對目標射擊1次，記命中目標的次數為[X]

（D）盒中有4個白球和3個黑球，每次從中摸出1個球且不放回，[X]是首次摸出黑球時的總次數

2. 已知100件產品中有10件次品，從中任取3件，則任意取出的3件產品中次品數的數學期望為______.

3. 在10件產品中有2件次品，連續抽3次，每次抽1件，求：

（1）不放回抽樣時，抽取次品數[ξ]的均值；

（2）有放回抽樣時，抽取次品數[η]的均值.

【設計意圖】第1題和第2題檢測學生對本節課重點內容的理解和掌握程度，檢查學生能否準確識別超幾何分布模型，能否求出超幾何分布的分布列和數學期望；第3題檢測學生對二項分布和超幾何分布區別的理解程度，是對本節課難點知識教學效果的即時檢測.

環節6：布置作業，應用遷移.

作業1：舉出一個服從超幾何分布的隨機變量的例子.

作業2：教材第81頁習題7.4第4題、第6題和第8題.

【設計意圖】通過自主舉例作業題的布置，加強學生對超幾何分布概念的理解；通過教材習題強化學生對本節課所學知識的掌握，進一步提升學生的數學抽象和數學建模素養.

參考文獻：

［1］中華人民共和國教育部. 普通高中數學課程標準（2017年版2020年修訂）［M］. 北京：人民教育出版社，2020.

［2］史寧中，王尚志.《普通高中數學課程標準（2017年版2020年修訂）》解讀［M］. 北京：高等教育出版社，2020.

［3］章建躍. 高中數學教科書教學設計與指導（選擇性必修第三冊）［M］. 上海：華東師范大學出版社，2022.