基于反步自適應(yīng)的多余度電靜壓伺服系統(tǒng)容錯控制研究

皇甫雨石，陳克勤，張 朋，張曉莎，郝偉一

基于反步自適應(yīng)的多余度電靜壓伺服系統(tǒng)容錯控制研究

皇甫雨石，陳克勤，張 朋，張曉莎，郝偉一

（北京精密機電控制設(shè)備研究所，北京，100076）

為滿足運載火箭高可靠性應(yīng)用需求，針對多余度電靜壓伺服系統(tǒng)（Electro-Hydrostatic Actuator，EHA）提出了基于反步自適應(yīng)的容錯控制策略，建立了數(shù)學(xué)模型及狀態(tài)空間方程，采用動態(tài)面方法降低了算法復(fù)雜性，實現(xiàn)了在冗余動力通道局部失效工況下的主動容錯控制，進行了仿真分析和試驗驗證。結(jié)果表明，相比于非線性PID控制，基于反步自適應(yīng)容錯控制策略可顯著降低系統(tǒng)在一路動力通道失效工況下的跟蹤誤差，提高系統(tǒng)控制性能，為未來工程應(yīng)用奠定基礎(chǔ)。

反步自適應(yīng)；容錯控制；電靜壓伺服系統(tǒng)；多余度

0 引 言

電靜壓伺服系統(tǒng)（Electro-Hydrostatic Actuator，EHA）具有抗污染能力強、效率高、負載能力強、易于冗余等特點[1]，已在航空、航海等領(lǐng)域廣泛應(yīng)用[2-3]。多余度EHA通過對易故障元組件進行硬件冗余，可顯著提高系統(tǒng)可靠性。在航天領(lǐng)域MOOG公司研制了一款四余度EHA用于運載火箭推力矢量控制[4]，可滿足兩路動力通道失效下的工作需求。立足于中國未來運載火箭高可靠性的應(yīng)用需求，項目團隊研制了具有良好性能的高集成多余度EHA樣機[5]，其動靜態(tài)性能已滿足運載火箭要求。

目前，國內(nèi)外學(xué)者在EHA動靜態(tài)性能提升方面，基于傳統(tǒng)控制和現(xiàn)代控制已開展較多研究[6-7]，而對于多余度EHA的容錯控制策略研究相對較少。為實現(xiàn)動力通道局部失效工況下的容錯控制，可采用神經(jīng)網(wǎng)絡(luò)、模糊推理等技術(shù)對系統(tǒng)動力組件進行故障診斷，利用故障信息結(jié)合控制律重構(gòu)等方法提高系統(tǒng)控制增益[8]，從而減小系統(tǒng)跟蹤誤差。此類方法對系統(tǒng)故障的判斷準確度要求較高，一般需要大量不同故障模式下的實驗數(shù)據(jù)作為支撐，工程實現(xiàn)較為復(fù)雜。

為提升伺服系統(tǒng)動力通道局部失效工況下的工作性能，本文以三余度電靜壓伺服系統(tǒng)為研究對象，提出了基于反步自適應(yīng)的主動容錯控制策略，建立了系統(tǒng)數(shù)學(xué)模型和狀態(tài)空間方程，通過仿真和試驗驗證了算法的正確性和可行性。結(jié)果表明在系統(tǒng)發(fā)生動力通道失效故障時，反步自適應(yīng)容錯控制策略能顯著提高系統(tǒng)的跟蹤響應(yīng)特性，且工程實用性好，易于實現(xiàn)。

1 技術(shù)方案

三余度EHA主要由控制驅(qū)動模塊、伺服電機泵動力模塊、余度管理模塊和作動器模塊組成。其中控制驅(qū)動模塊和伺服電機泵動力模塊采用三余度設(shè)計，每臺伺服控制驅(qū)動器單獨控制一臺伺服電機泵的轉(zhuǎn)向和轉(zhuǎn)速，通過流量綜合改變作動器活塞桿的運動方向和速度。當一路動力通道失效時，可通過隔離閥進行故障隔離。其工作原理見圖1，主要設(shè)計參數(shù)見表1。

圖1 三余度EHA工作原理

表1 三余度EHA主要設(shè)計參數(shù)

Tab.1 Main design parameters of the triple EHA

參數(shù)數(shù)值 活塞桿行程/mm±75 柱塞泵排量/(mL·轉(zhuǎn)-1)1.26 活塞桿有效面積/mm24398 最高工作壓力/MPa21 工作電壓/V270 電機最大轉(zhuǎn)速/(轉(zhuǎn)·min-1)18000 負載最大擺角/(°)6 負載轉(zhuǎn)動慣量/(kg·m2)1140

2 數(shù)學(xué)模型建立

建立伺服系統(tǒng)數(shù)學(xué)模型，其中慣性負載環(huán)節(jié)簡化為單質(zhì)量彈簧系統(tǒng)，伺服電機簡化為二階環(huán)節(jié)，忽略伺服作動器等效質(zhì)量，具體如下：

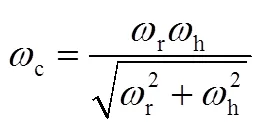
式中p為柱塞泵排量；為電機泵轉(zhuǎn)速；為機構(gòu)工作動力通道數(shù)；為活塞有效面積；c為活塞桿位移；為系統(tǒng)總泄漏系數(shù)；t為作動筒兩腔總?cè)莘e；e為油液有效體積彈性模量；L為負載壓力；sr為連接結(jié)構(gòu)剛度；L為負載位移；L為活塞及折算到其上的總質(zhì)量；L為負載粘性阻尼；為作用在負載上的外力；為負載轉(zhuǎn)動慣量；為伺服機構(gòu)搖擺負載力臂；r為負載結(jié)構(gòu)諧振頻率；r為負載結(jié)構(gòu)等效阻尼比；h為液壓固有頻率；c為機械液壓綜合諧振頻率；c為機械液壓綜合諧振阻尼比；m為伺服電機等效傳遞函數(shù)；m為伺服電機等效自然頻率；m為伺服電機等效阻尼比；v為伺服電機增益系數(shù)；為伺服電機控制電壓。

合并式（1）至式（3）進行拉普拉斯變換，忽略作用在負載上的外力，結(jié)合式（4）至式（9），系統(tǒng)連續(xù)性方程表示為

忽略式（12）中分母高階項，可將系統(tǒng)連續(xù)性方程表示為

3 反步自適應(yīng)容錯控制策略

反步自適應(yīng)容錯控制策略由反步控制和自適應(yīng)容錯算法兩部分構(gòu)成，其控制結(jié)構(gòu)如圖2所示。根據(jù)系統(tǒng)相關(guān)變量建立自適應(yīng)估計律，并將其引入到反步控制策略中，得到最終控制量。系統(tǒng)工作過程中，通過自適應(yīng)估計律實時修正控制參數(shù)，實現(xiàn)故障工況下的主動容錯控制。控制策略滿足李雅普諾夫穩(wěn)定性定理，能夠保證系統(tǒng)閉環(huán)控制的穩(wěn)定。

圖2 反步自適應(yīng)容錯控制結(jié)構(gòu)

3.1 反步控制算法設(shè)計

選擇伺服機構(gòu)活塞桿位移、速度、加速度為狀態(tài)變量1、23，根據(jù)式（11）和式（13）建立系統(tǒng)狀態(tài)空間方程，忽略伺服電機環(huán)節(jié)，如式（14）所示。

對系統(tǒng)狀態(tài)變量分別定義跟蹤誤差：

求解控制律23、，算法設(shè)計過程如下：

選取李雅普諾夫函數(shù)：

選取李雅普諾夫函數(shù)：

選取李雅普諾夫函數(shù)：

3.2 自適應(yīng)容錯算法設(shè)計

為實現(xiàn)系統(tǒng)動力通道局部失效工況下的主動容錯控制，選取系統(tǒng)工作動力通道數(shù)構(gòu)建自適應(yīng)估計律。

定義李雅普諾夫函數(shù)：

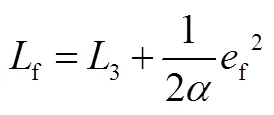
對式（24）進行求導(dǎo)：

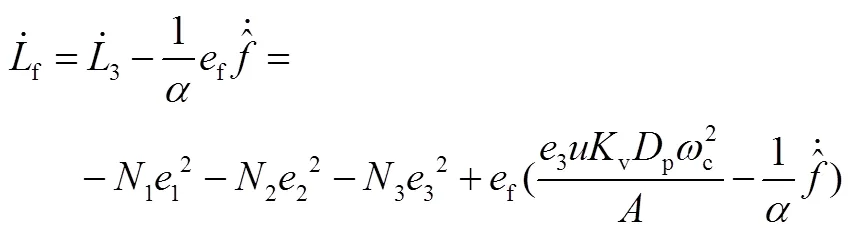
式中(0)為參數(shù)初值。

3.3 動態(tài)面設(shè)計

系統(tǒng)實際控制律中包含多個虛擬控制律的微分求解過程，導(dǎo)致計算過程較為復(fù)雜，容易引起微分爆炸及計算膨脹問題[9]。為減少算法中涉及到的微分環(huán)節(jié)，同時提高信號輸出的平滑性，采用動態(tài)面法對系統(tǒng)控制策略進行優(yōu)化。

動態(tài)面設(shè)計為

式中為動態(tài)面參數(shù)；3f為動態(tài)面輸出。

系統(tǒng)實際控制律式（22）更新為

由于濾波誤差的產(chǎn)生，使式（25）更新為

根據(jù)Young’s不等式關(guān)系可得：

根據(jù)Bellman-Gronwall[10]不等式關(guān)系可得：

此外系統(tǒng)控制律中高階控制項的存在，導(dǎo)致控制信號響應(yīng)復(fù)雜[11]，工程應(yīng)用中關(guān)注中低頻段，故消除二階及以上階次的控制項，簡化后的反步自適應(yīng)容錯控制律可表示為

建立基于反步自適應(yīng)容錯控制策略的三余度EHA數(shù)學(xué)仿真模型，如圖3所示，模型參數(shù)如表2所示。

表2 三余度EHA模型主要參數(shù)

Tab.2 Model parameters of the triple EHA

參數(shù)數(shù)值 電機等效自然頻率ωm/(rad·s-1)120 電機等效阻尼比ξm0.707 負載結(jié)構(gòu)諧振頻率ωr/(rad·s-1)100 負載結(jié)構(gòu)諧振阻尼比ξr0.04 機械液壓綜合諧振頻率ωc/(rad·s-1)90 機械液壓綜合諧振阻尼比ξc0.1

4 仿真分析及試驗驗證

為驗證反步自適應(yīng)容錯控制策略的有效性，進行仿真和試驗驗證，并與非線性PID算法進行對比，非線性PID數(shù)學(xué)表達式為[12]

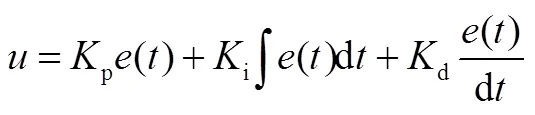
式中p為非線性PID中與誤差()相關(guān)的比例項增益；，，為比例項系數(shù)；i為非線性PID積分項增益；d為非線性PID微分項增益。

仿真與試驗過程中，伺服系統(tǒng)初始工況為三路動力通道同時工作，通過隔離閥模擬一路動力通道失效，使系統(tǒng)切換為兩路動力通道工作，驗證2種控制策略下系統(tǒng)跟蹤性能。控制算法主要參數(shù)如表3所示。

表3 控制算法參數(shù)

Tab.3 Control algorithm parameter

反步自適應(yīng)容錯控制非線性PID控制 參數(shù)數(shù)值參數(shù)數(shù)值 N140a10 N240b5 N330c5 ε0.03Ki0 α8×10-8Kd0

4.1 非線性PID算法仿真及試驗

給定系統(tǒng)幅值為2°，頻率為0.2 Hz的正弦信號，非線性PID控制算法仿真與試驗結(jié)果如圖4所示。

圖4 非線性PID控制仿真與試驗曲線

由圖4a可看出，在6.9 s時刻由三路動力通道切換為兩路動力通道，系統(tǒng)增益降低約33%，輸出流量減小，系統(tǒng)跟蹤誤差由0.11°增大至0.21°，增幅約90%；由圖4b可看出，電機轉(zhuǎn)速峰值由3900 轉(zhuǎn)/min增加至7700 轉(zhuǎn)/min，驅(qū)動電流由5.9 A增加至11.5 A，但由于系統(tǒng)增益降低導(dǎo)致相位滯后增加，使系統(tǒng)在一路動力通道失效的工況下位置跟蹤誤差增大，控制性能降低。

4.2 反步自適應(yīng)容錯算法仿真及試驗

圖5 反步自適應(yīng)容錯控制仿真與試驗曲線

c）伺服電機轉(zhuǎn)速與電流

續(xù)圖5

5 結(jié)束語

本文針對多余度電靜壓伺服系統(tǒng)提出了基于反步自適應(yīng)的主動容錯控制策略，采用動態(tài)面方法降低了控制算法復(fù)雜性，仿真和試驗結(jié)果表明，該控制策略能夠有效降低伺服系統(tǒng)動力通道局部失效工況下的跟蹤誤差，提高了系統(tǒng)控制性能，為工程應(yīng)用奠定基礎(chǔ)。

[1] 曾廣商, 趙守軍, 張曉莎. 我國載人運載火箭伺服機構(gòu)技術(shù)發(fā)展分析[J]. 載人航天, 2013, 19(4): 3-10.

ZENG Guangshang, ZHAO Shoujun, ZHANG Xiaosha. Technology development analysis of Chinese servo-mechanisms for human-rated launch vehicles[J]. Manned Space flight, 2013, 19(4): 3-10.

[2] SHANG Yaoxing, LI Xiaobin, QIAN Hao, et al. A novel electro hydrostatic actuator system with energy recovery module for more electric aircraft[J]. IEEE Transactions on Industrial Electronics, 2020, 67(4): 2991-2999.

[3] TAKAHASHI N, KONDO T, TAKADA M, et al. Development of prototype electro-hydrostatic actuator for landing gear extension and retraction system[C]. Toyama: the 7th JFPS International Symposium on Fluid Power, 2008.

[4] GARRISON Michael, STEFFAN S. Two fault tolerant electric actuation systems for space applications[C]. Sacramento: 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference, 2006.

[5] 陳克勤, 趙守軍, 劉會祥, 等. 運載火箭大功率多余度電靜壓伺服機構(gòu)技術(shù)研究[J]. 導(dǎo)彈與航天運載技術(shù), 2020(2): 79-84.

CHEN Keqin, ZHAO Shoujun, LIU Huixiang, et al. The study on the high power redundant electro-hydrostatic actuator for launch vehicles[J]. Missiles and Space Vehicles, 2020(2): 79-84.

[6] 高詩程, 張朋, 趙守軍, 等. 電靜壓伺服系統(tǒng)指數(shù)型變阻尼滑模控制算法研究[J]. 導(dǎo)彈與航天運載技術(shù), 2022(3): 112-118.

GAO Shicheng, ZHANG Peng, ZHAO Shoujun, et al. Study on an exponential variable damping sliding mode control algorithm for an electro-hydrostatic actuator[J]. Missiles and Space Vehicles, 2022(3): 112-118.

[7] 任彬, 祁曉野. 基于模糊PID的電動靜液作動器位置控制系統(tǒng)[J]. 自動化與儀表, 2018, 33(4): 10-15.

REN Bin, QI Xiaoye. Electric hydrostatic actuator position control system based on fuzzy PID[J]. Automation & Instrumentation, 2018, 33(4): 10-15.

[8] 趙春. 機電靜壓伺服系統(tǒng)余度技術(shù)研究[D]. 北京: 中國運載火箭技術(shù)研究院, 2015.

ZHAO Chun. Study on the redundancy design of electro-hydrostatic actuators[D]. Bejing: China Academy of Launch Vehicle Technology, 2015.

[9] SWAROOP D, HEDRICK J K, YIP P P, Gerdes J C. Dynamic surface control for a class of nonlinear systems[J]. IEEE Transactions on Automatic Control, 2000, 45(10): 1893-1899.

[10] GRONWALL T H. Note on the derivatives with respect to a parameter of the solutions of a system of differential equations[J]. Annals of Mathematics, 1919, 20(4): 292-296.

[11] 張紹峰, 金曉宏, 周園, 等. 被動式電液力系統(tǒng)反步控制算法的簡化研究[J]. 機電工程, 2022, 39(7): 928-934.

ZHANG Shaofeng, JIN Xiaohong, ZHOU Yuan, et al. Simplification of backstepping control algorithm for passive electro hydraulic system[J]. Journal of Mechanical & Electrical Engineering, 2022, 39(7): 927-934.

[12] 劉璐. 大功率機電靜壓伺服系統(tǒng)控制策略研究[D]. 北京: 中國運載火箭技術(shù)研究院, 2017.

LIU Lu. Study on the control strategy of a high power electro-hydrostatic actuator[D]. Bejing: China Academy of Launch Vehicle Technology, 2017.

Study on Fault Tolerance Control of Redundant Electro-hydrostatic Actuator based on Backstepping Adaptive

HUANGFU Yushi, CHEN Keqin, ZHANG Peng, ZHANG Xiaosha, HAO Weiyi

(Beijing Institute of Precision Mechatronics and Controls, Beijing, 100076)

In order to meet the application requirements of high reliability of launch vehicle, a fault tolerant control strategy based on backstepping adaptive is proposed for redundant electro-hydrostatic actuator. The mathematical model and state space equation are established. The dynamic surface method is used to reduce the complexity of the control algorithm, and the active fault tolerant control under redundant power channel local failure condition is realized. The simulation analysis and experimental verification are completed. The results show that compared with the nonlinear PID, the backstepping adaptive fault tolerant control can significantly reduce the tracking error of the system under the failure condition of one power channel, improve system control performance, and lay a foundation for future engineering applications.

backstepping adaptive; fault tolerant control; electro-hydrostatic actuator; redundant

2097-1974(2023)02-0052-06

10.7654/j.issn.2097-1974.20230211

V433

A

2023-01-29；

2023-02-03

皇甫雨石（1998-），男，碩士研究生，主要研究方向為伺服控制技術(shù)。

陳克勤（1984-），男，研究員，主要研究方向為伺服系統(tǒng)設(shè)計。

張 朋（1984-），男，高級工程師，主要研究方向為伺服系統(tǒng)設(shè)計。

張曉莎（1964-），女，研究員，主要研究方向為伺服系統(tǒng)設(shè)計。

郝偉一（1989-），男，工程師，主要研究方向為伺服系統(tǒng)設(shè)計。