TSTO 并聯分離激波/邊界層干擾流動特性分析

范孝華，張慶虎，羅 磊，林敬周，唐志共

(1. 中國空氣動力研究與發展中心 超高速空氣動力研究所，綿陽 621000；2. 中國空氣動力研究與發展中心 計算空氣動力研究所，綿陽 621000；3. 中國空氣動力研究與發展中心，綿陽 621000)

0 引 言

兩級入軌飛行器（two-stage-to-orbit, TSTO）是一種可重復使用的航天運載器（reusable launch vehicle,RLV），能夠實現高頻快速進出空間，遂行不同類型的飛行任務，大幅降低航天運輸成本。其作為極具潛力的空天運輸系統，一直受到國內外廣泛關注[1-8]。

級間分離問題直接決定了飛行任務的成敗，是TSTO 飛行器必須解決的關鍵問題[9]。助推級與軌道級并聯布局的TSTO 級間分離馬赫數一般設計在超聲速或者高超聲速范圍[10]，分離過程需要經歷組合體流動、縫隙流、小通道流、大通道流，直至無干擾流動，其間涉及三維激波/激波干擾以及激波/邊界層干擾等復雜流動。這些復雜流動會引起飛行器表面的邊界層流動狀態以及壓力和熱流載荷急劇變化，進而對兩級飛行器分離過程的氣動特性產生顯著影響，甚至可能破壞飛行器表面、威脅分離的安全性，導致事故發生。深入理解和認識TSTO 級間產生氣動干擾的流動機理，探索削弱氣動干擾強度的途徑，可以為飛行器氣動設計以及分離方案的選擇提供有益參考。

Ozawa 等[11]采用半球-圓柱模型作為軌道級，助推級則分別選擇三角翼以及構型更工程化的高超聲速助推級模型，通過風洞試驗獲取馬赫數8.1 模型周圍的流場特征以及模型壁面熱流分布；研究發現高超聲速助推級模型前緣產生了強的頭激波，增加了流過氣流的總壓損失，進而削弱了兩級模型間的激波/激波和激波/邊界層干擾強度。Uematsu 等[12-14]同樣選擇半球-圓柱模型作為軌道級，而助推級則采用截面分別為方形、圓形以及三角形的細長體模型，在馬赫數4 條件下開展不同級間距的試驗與數值研究；分析了模型周圍流場結構、模型表面壓力分布以及氣動力特性，發現橫截面為三角形的助推級對反射激波的減弱效應最強，進而使得級間的干擾強度下降最多。王粵等[15]將TSTO 助推級和軌道級簡化為兩個三維楔，基于重疊網格開展馬赫數7 條件下層流狀態不同軌道級抬升角度的靜態與動態數值模擬；獲得兩級表面壓力載荷、流場結構以及三維流動分離拓撲結構，研究分析級間氣動干擾對TSTO 氣動分離的影響機制。Jia 等[16]針對軌道級為鈍頭錐 + 圓柱 + 翼構型、助推級為梯形翼的TSTO 模型，通過數值模擬研究了馬赫數8.1 條件下不同級間距的級間氣動干擾流場，發現激波/邊界層干擾導致的壁面壓力與熱流的躍升隨著級間距的增大而減弱。Cheng 等[17]以寬速域飛行器為軌道級，以帶翼火箭為助推級，通過數值模擬研究了TSTO 飛行器馬赫數6 條件下的熱環境。他們分析發現，火箭頭部產生的激波入射到軌道級，并在級間產生逐漸減弱的系列反射激波。雖然激波相對溫和，沒有導致邊界層發生分離，但激波作用于壁面還是產生了較高的熱流區域；并且隨著飛行器攻角的減小，軌道級迎風面的熱流呈下降趨勢。

已有的研究表明，即使是較為簡單的TSTO 外形，級間激波主導的干擾流場也呈現出顯著的三維特征。隨著TSTO 氣動構型的工程化，級間的流動結構和干擾模式變得更為復雜和多樣。唐偉等[18]基于建立滿足飛行原理、帶有共性特征、反映氣動特性、適合風洞試驗的研究模型的考慮，設計了如圖1 所示的背負式TSTO 氣動構型方案，旨在為級間干擾和動態分離研究提供研究對象。Peng 等[19]針對唐偉等的TSTO 標模進行縮比和適當簡化，在馬赫數6 來流條件下開展快響應壓敏漆（pressure sensitive paint, PSP）和溫敏漆（temperature sensitive paint, TSP）試驗，獲得不同級間距及攻角條件下激波作用于壁面的干擾區域壓力和溫度分布。為進一步探索TSTO 標模級間激波/邊界層干擾流動機理，本文采用多種試驗測量技術以及數值模擬手段，精細刻畫典型級間距以及不同流態條件下模型表面及空間的流動特征，揭示TSTO 級間復雜三維激波/邊界層干擾流動特性。

圖1 TSTO 氣動布局方案[18]Fig. 1 TSTO conceptual configuration[18]

1 試驗與數值方法

1.1 研究對象

本文將TSTO 標模進行適當的縮比和簡化后作為研究對象，如圖2 所示。

圖2 TSTO 模型示意圖（單位：mm）Fig. 2 TSTO model configuration (unit: mm)

助推級為橢圓錐導前機身 + 邊條后掠翼 + 雙垂尾構型，上壁面削平形成的突起平臺用于安放軌道級，軌道級為翼身組合體。本研究重點關注助推級與軌道級之間的干擾流場，因此將助推級機身下壁面簡化為了平面，機翼簡化后去掉下折的機翼翼梢，去掉軌道級上部垂尾。根據風洞對模型尺寸的約束，模型幾何縮比為1∶160，助推級模型總長LB=531 mm，翼展WB=255 mm；軌道級模型總長LO=219 mm，翼展寬度WO=109 mm；軌道級與助推級呈上下并聯布置，水平方向上軌道級頭部固定在助推級前緣下游d=206 mm處。助推級上壁面與軌道級下壁面之間的距離定義為級間距h。坐標系固定于助推級上壁面，以軌道級頭部頂點在助推級上的投影為原點，x軸與來流方向一致，y軸垂直助推級上壁面并向上，z軸滿足右手定則。為便于不同尺度模型之間的對比與關聯，模型坐標值及級間距均以軌道級長度LO作為參考長度進行無量綱化。

1.2 試驗設備與來流條件

風洞試驗在中國空氣動力研究與發展中心超高速所Φ0.5 m 高超聲速風洞中開展。該風洞是一座暫沖吹吸式常規高超聲速風洞，單次風洞的有效試驗時間可超過30 s，總壓和總溫控制精度優于1%。試驗來流馬赫數Ma=6，總壓p0=1 890 kPa，總溫T0=492 K。 表1 給出了自由來流的具體參數，其中p∞、T∞和Rel分別表示來流靜壓、靜溫以及單位雷諾數。

表1 自由來流條件Table 1 Freestream conditions

1.3 試驗方法

試驗時，助推級模型采用具有法向間距調節能力的腹部支撐，軌道級模型采用尾支撐；兩級模型攻角和側滑角均為0°；兩級模型的無量綱級間距分別為h/LO=0.023、0.051和0.123，其中級間距h/LO=0.023條件下的流動為分離初始產生的縫隙流，h/LO=0.051條件下的流動為級間具有多次激波反射的典型小通道流動，而h/LO=0.123條件下的流動為隨著分離距離增大級間激波反射已減少至1 次時的末期小通道流動。

試驗通過紋影和納米示蹤的平面激光散射（nano-tracer-based planar laser scattering, NPLS）非接觸測量技術顯示模型級間激波/邊界層干擾流場結構，熒光油流用于獲取助推級上表面流譜，在級間上下壁面沿流向布置靜壓測點以獲取不同級間距的壓力信息。

紋影光路呈“Z”形布置，觀察窗口直徑為500 mm，紋影相機分辨率為2048 × 2048，采樣速率為25 幀/s。NPLS 測量通過在流場中注入二氧化碳氣體，在經過噴管膨脹時凝結成干冰微團作為示蹤粒子；厚度小于1 mm 的脈沖激光片光照射模型中心平面流場，分辨率為2048 × 2048 的CCD 相機采集干冰產生的瑞利散射瞬時圖像。油流測量需要在試驗前將混合熒光粉的硅油均勻噴涂到模型表面，試驗過程中通過在風洞試驗段上方布置高速攝影儀獲取熒光油流流動圖譜，圖像分辨率為1920 × 1080，采樣速率為69 幀/s。

試驗通過DTC initium 電子掃描壓力測量系統測量級間壁面靜壓，其中在助推級上壁面中心線x/LO=0.11～1.21范圍內均布13 個靜壓測點，在展向z/LO=0.046處x/LO=0.47～1.21范圍內均布5 個測點；在軌道級下壁面中心線x/LO=0.27～0.84范圍內均布13 個靜壓測點，在展向z/LO=0.027處x/LO=0.27～0.89范圍內均布10 個測點。所有測點通過管道連接到上量程為69 kPa 的掃描模塊上，綜合測量精度優于±0.1% FS。

1.4 數值模擬方法

定常數值模擬用于獲取更多的級間空間流場信息。不考慮側滑情況，選取半模進行計算。計算采用中國空氣動力研究與發展中心自主研發的非結構計算流體力學軟件NNW-FlowStar[20]。該求解器基于二階非結構混合網格的格心型有限體積方法。選擇HLLE + + 格式和Venkatakrishnan 限制器，保證空間為二階精度；分別采用層流和k-ωSST 湍流模型進行黏性模擬，用以對比不同黏性模式對模擬結果的影響。邊界條件使用無反射的超聲速壓力遠場和對稱面邊界，壁面采用等溫壁條件（Tw=300 K）；計算的自由來流條件與試驗保持一致（詳見表1）。

計算流場空間采用四面體非結構網格，近壁區域采用加密四面體棱柱網格，以期更為精確地刻畫近壁區域的流場細節。為提高級間復雜反射波系結構及激波/邊界層干擾引起的流動分離區域的分辨率，本文特使用了NNW-FlowStar 軟件內置的網格自適應模塊[21]。針對級間復雜流動特征結構，本文采用激波判別法（特征線判別[22]）用于識別和標記目標特征。針對目標網格分布，本文采用“H”形（剖分式）自適應技術對網格進行優化（如圖3 所示）。

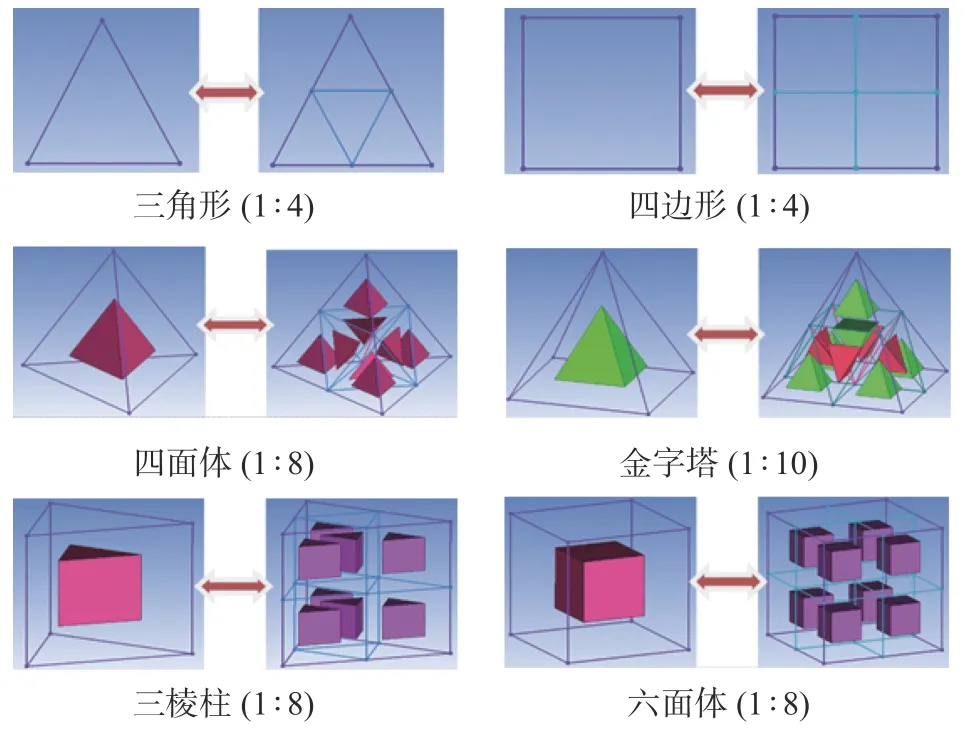
圖3 網格自適應加密方式[21]Fig. 3 Adaptive mesh refinement approaches[21]

圖4 對比了有、無網格自適應加密條件下，級間距h/LO=0.051的層流計算結果，分別給出了馬赫數云圖、壓力系數云圖為自由來流動壓）及模型表面與對稱面網格示意圖。如圖4（a）所示，無網格自適應加密得到的激波波面不夠銳利，級間流場也不夠細致。而使用網格自適應模塊后，網格量由600 萬左右增加至2300 萬左右，網格沿著激波所在的區域加密，使得激波和流場的模擬更為精細，結果如圖4（b）所示。

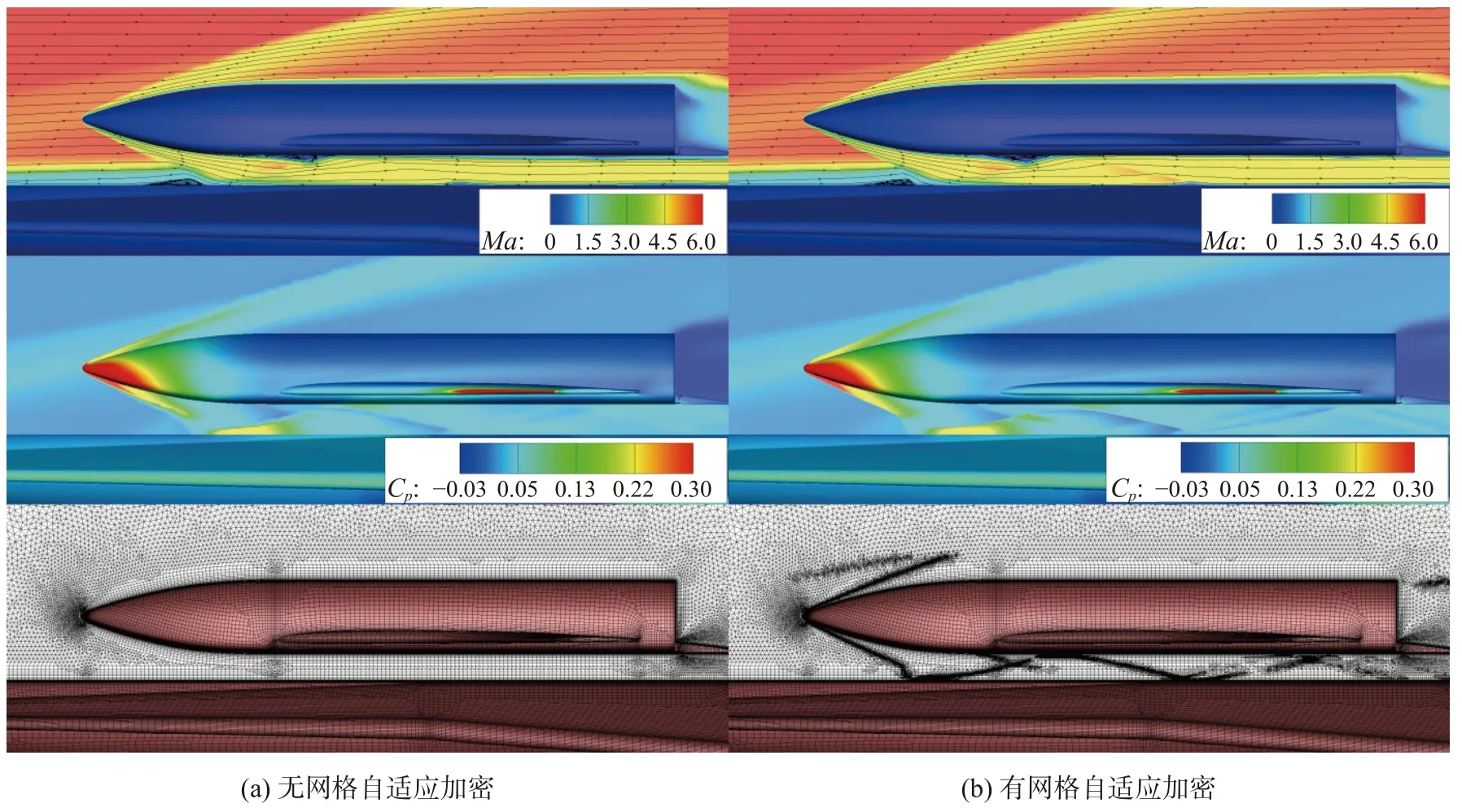
圖4 有、無自適應網格加密的層流計算流場Fig. 4 Laminar flow field with/without adaptive mesh refinement

2 結果及討論

2.1 壁面邊界層流態

圖5 給出了h/LO=0.023、0.051、0.123三個典型級間距下的NPLS 圖像。

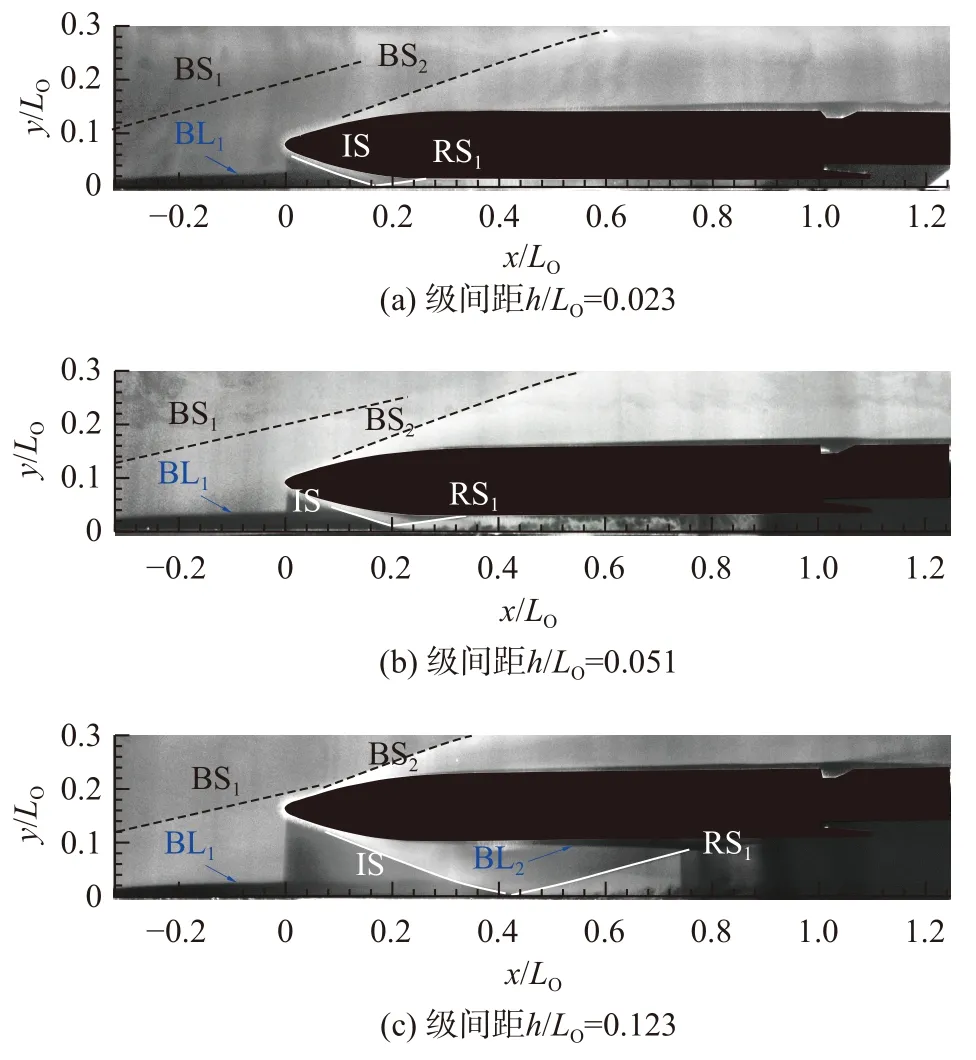
圖5 典型級間距條件下的NPLS 圖像Fig. 5 NPLS of flow fields within typical stage clearances

在激波入射之前，助推級和軌道級的壁面邊界層（BL1和BL2）均處于層流狀態。當激波IS 入射到助推級上壁面層流邊界層時，流動分離發生，同時分離泡以及剪切層引起的流動不穩定性使得反射激波RS1下游的再附邊界層迅速轉捩為湍流狀態[23-25]。對于小級間距h/LO=0.023的情況，助推級上壁面x/LO=0處（軌道級頭部頂點的垂直下方）的層流邊界層厚度yδ/LO≈0.038（u/ue=0.99處，如圖6 所示），大于級間間隙高度，級間處于邊界層內的低動量流動狀態，甚至可能發生“雍塞”的情況，因此在NPLS圖像中級間沒有呈現顯著的流動結構。對于級間距h/LO=0.051，反射激波RS1同樣導致了軌道級下壁面邊界層迅速轉捩為湍流。而對于級間距h/LO=0.123，RS1入射點靠近軌道級模型尾部，干擾后的邊界層不在激光照射區域內，并且在激波強度不夠的條件下有可能發生邊界層在激波入射后仍然保持層流的情況[24]，因此無法判斷RS1激波作用之后的邊界層流態。

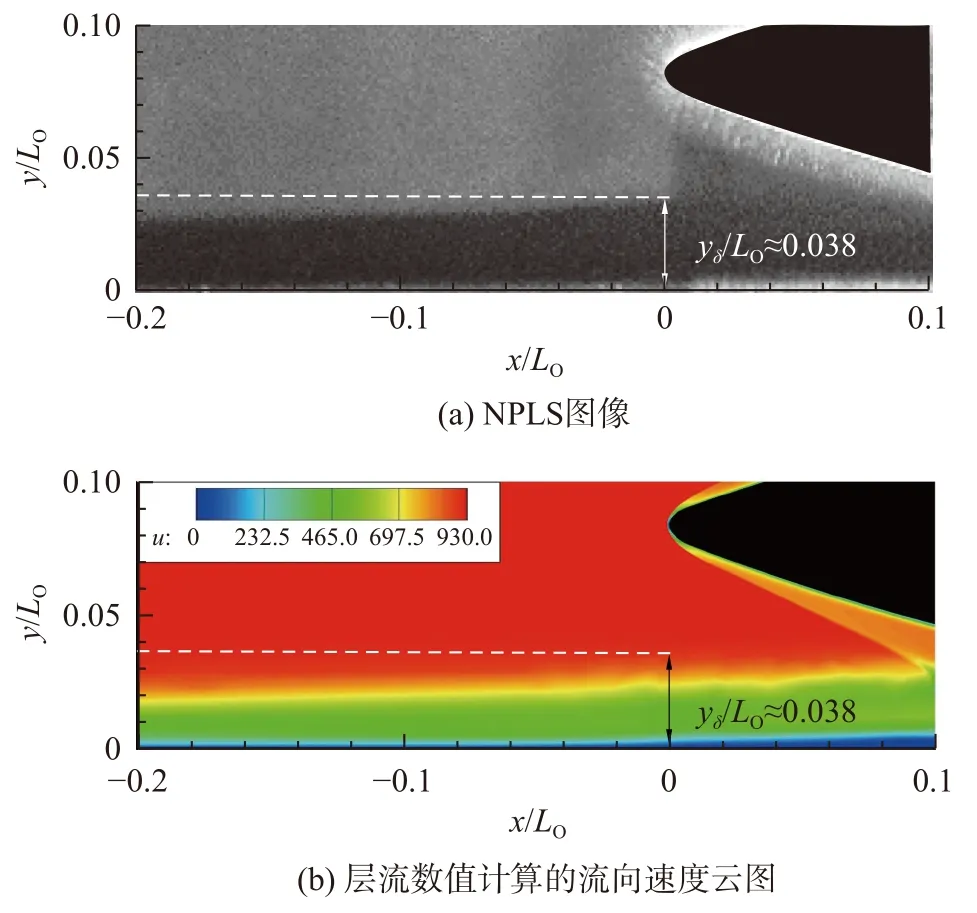
圖6 助推級上壁面x/LO = 0 處邊界層厚度Fig. 6 Boundary layer thickness over the upper booster wall at x/LO = 0

鑒于級間距h/LO=0.051的級間流場具有典型的激波/邊界層三維多波系復雜干擾結構特征，本文針對該級間距進行了詳細的流動特性分析。

2.2 級間波系結構

圖7 給出了級間距h/LO=0.051的試驗紋影與數值模擬的對稱面密度梯度云圖，以虛線標示出激波的形狀。助推級頭部產生的弱斜激波為BS1；軌道級頭部產生的激波分別為BS2以及IS，IS 作用于助推級上壁面導致邊界層流動分離，并形成反射激波RS1。由于層流邊界層抵抗逆壓梯度的能力較弱，RS1作用到軌道級下壁面層流邊界層時形成大尺度的流動分離，產生較強的分離激波SS1（紅色虛線標示），其作用于助推級上壁面后還能形成反射激波SS2（見圖7（b））；同時，RS1在軌道級下壁面形成的反射激波RS2作用于助推級層流邊界層時同樣產生分離激波SS3和反射激波RS3，并最終在軌道級尾部產生系列壓縮波系。而對于湍流狀態（見圖7（c）），RS1在軌道級下壁面形成的流動分離尺度較小，產生的分離激波SS1強度較弱，同時RS1在級間壁面來回反射，依次形成反射激波RS2、RS3以及RS4，在這些激波入射位置未見明顯的流動分離結構。

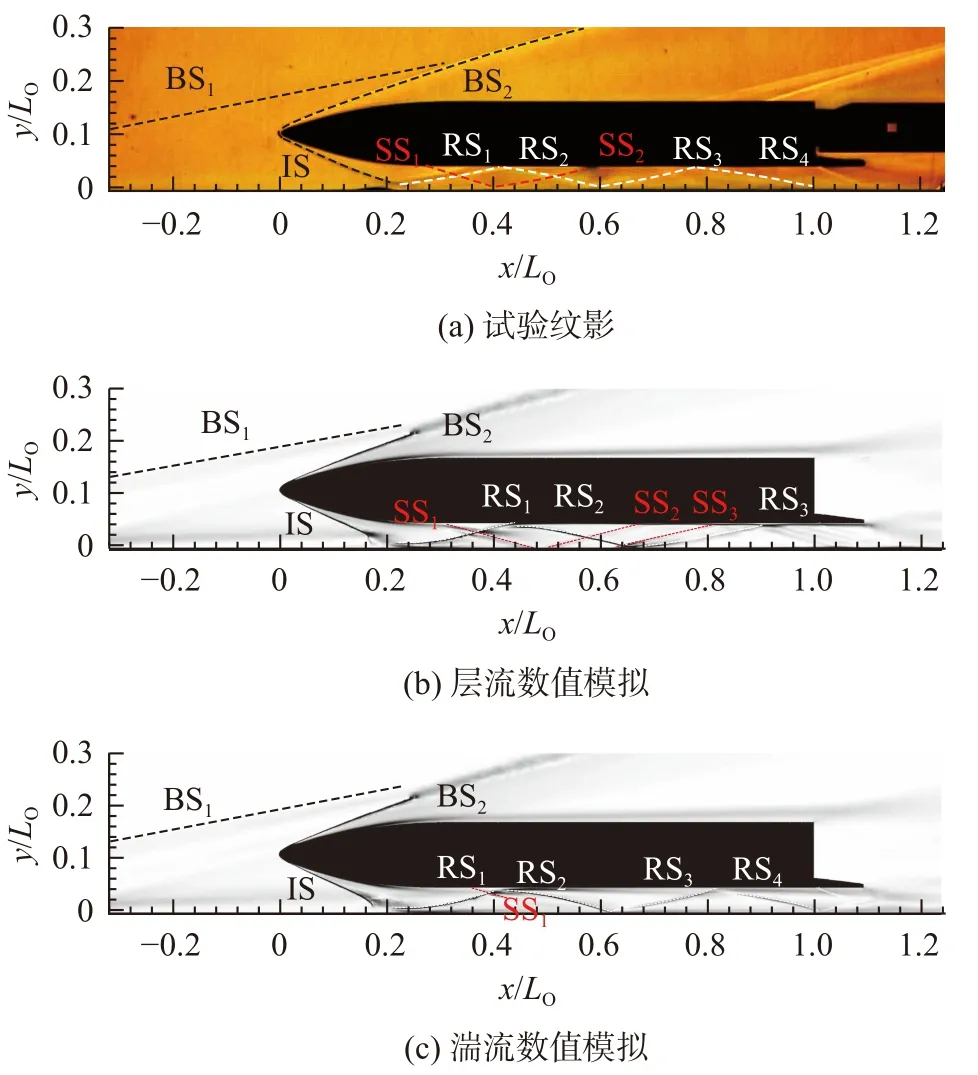
圖7 試驗紋影與計算密度梯度圖Fig. 7 Schlieren result and computed density gradient

圖8 給出了助推級和軌道級相對壁面中心線及展向特定位置的試驗與計算的流向壓力系數分布。在激波IS 入射前，助推級上壁面先后經歷壓縮與膨脹后，中心線壁面壓力已下降到接近于來流靜壓的平穩狀態。當入射激波IS 作用于壁面邊界層后，流動分離與再附發生，在中心線x/LO=0.276處引起最大壓力躍升（位于反射激波RS1起始點下游），對應的層流和湍流壓力系數分別達到0.252 和0.234。而軌道級由于頭部下壁面凸曲面構型產生的膨脹波的影響，壁面壓力持續下降，反射激波RS1入射軌道級下壁面邊界層，并在其中心線x/LO=0.471壁面處引起最大壓力躍升，對應的層流和湍流壓力系數分別是0.118 和0.117。隨后產生的反射激波強度逐漸減弱，引起的壓力躍升也逐漸減小。值得注意的是，由于層流邊界層更易發生流動分離，其分離起始點較湍流狀態更靠近上游，導致層流邊界層受到激波IS 和RS1作用引起的壓力躍升起始點更靠前。特定展向位置的流向壓力變化趨勢與中心線基本一致，但具體的壓力系數值以及波系結構位置存在一定的差異，呈現出干擾的三維特征。此外，由于試驗中模型壁面邊界層在激波干擾之前為層流狀態，干擾后迅速轉捩為湍流狀態（見圖5（b）），因此試驗紋影及壓力測量結果在第一道激波（IS 或者RS1）的作用結束之前與層流計算結果一致，而在激波作用之后，與湍流計算結果吻合。

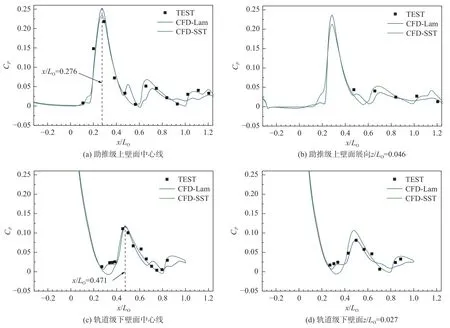
圖8 模型壁面的流向壓力分布Fig. 8 Streamwise variations of the wall pressure coefficients

2.3 壁面流動圖譜

圖9 （a）和圖9（b）分別給出了熒光油流試驗獲得的模型壁面流動圖譜和計算得到的壁面極限流線圖。試驗中，在入射激波IS 的作用下，助推級上壁面位于軌道級頭部下方兩側的肩部出現了對稱的旋渦結構，同時發現了旋渦下游沿流向方向的分離線；而位于軌道級垂直下方的干擾區因被遮擋，所以未能顯示。由于激波RS1的作用，軌道級下壁面x/LO=0.24附近靠近中心線區域出現了弧形的分離線，并且在分離線的兩端形成一對旋渦。通過對比試驗與計算的流線圖譜可以看出，層流計算結果在相應區域出現與試驗非常類似的流動結構，包括流動分離線與旋渦結構；而湍流計算結果與試驗存在較大的差異。這進一步說明在助推級上壁面和軌道級下壁面各自第一道激波干擾結束前的試驗流場更接近于層流狀態。

圖9 模型壁面流動圖譜Fig. 9 Flow topology at the wall

圖10（a）給出了激波IS 作用下的助推級上壁面干擾區局部放大圖。圖中層流和湍流結果以上下對稱方式給出，同時給出了壁面的壓力系數和壁面極限流線；用白色和藍色虛線分別刻畫分離線和再附線位置，并標示出干擾流場中的鞍點S、結點N 和焦點F，下標“b”表示位于助推級，上標“*”代表湍流結果。圖10（b）則給出了干擾區壁面中心線最大壓力系數處（x/LO=0.276，在圖10（a）用黑色虛線標示）橫截面的壓力系數云圖。結合壁面極限流線與壓力系數云圖可以看出，激波IS 引起的干擾區呈現顯著的三維特征。軌道級頭部產生的三維激波在周向空間上呈環狀分布（IS），在其入射助推級上壁面導致流動分離的同時，也形成了反射激波RS1和整體呈弧狀向下游展開的高壓區。在x/LO=0.276的橫截面處，反射激波RS1的波面在展向逐漸靠近助推級壁面，形成位于高壓區內中心線以及展向z/LO=0.04附近的兩個壓力峰值，層流狀態的展向壓力變化特征更為明顯。此外，壁面分離流動是開放的，即分離區的流線不再都起于分離線、止于再附線，干擾區內出現鞍點、結點、焦點等臨界點結構[26]，并且層流狀態的干擾流場區域要明顯大于湍流狀態，流場結構也更為復雜。

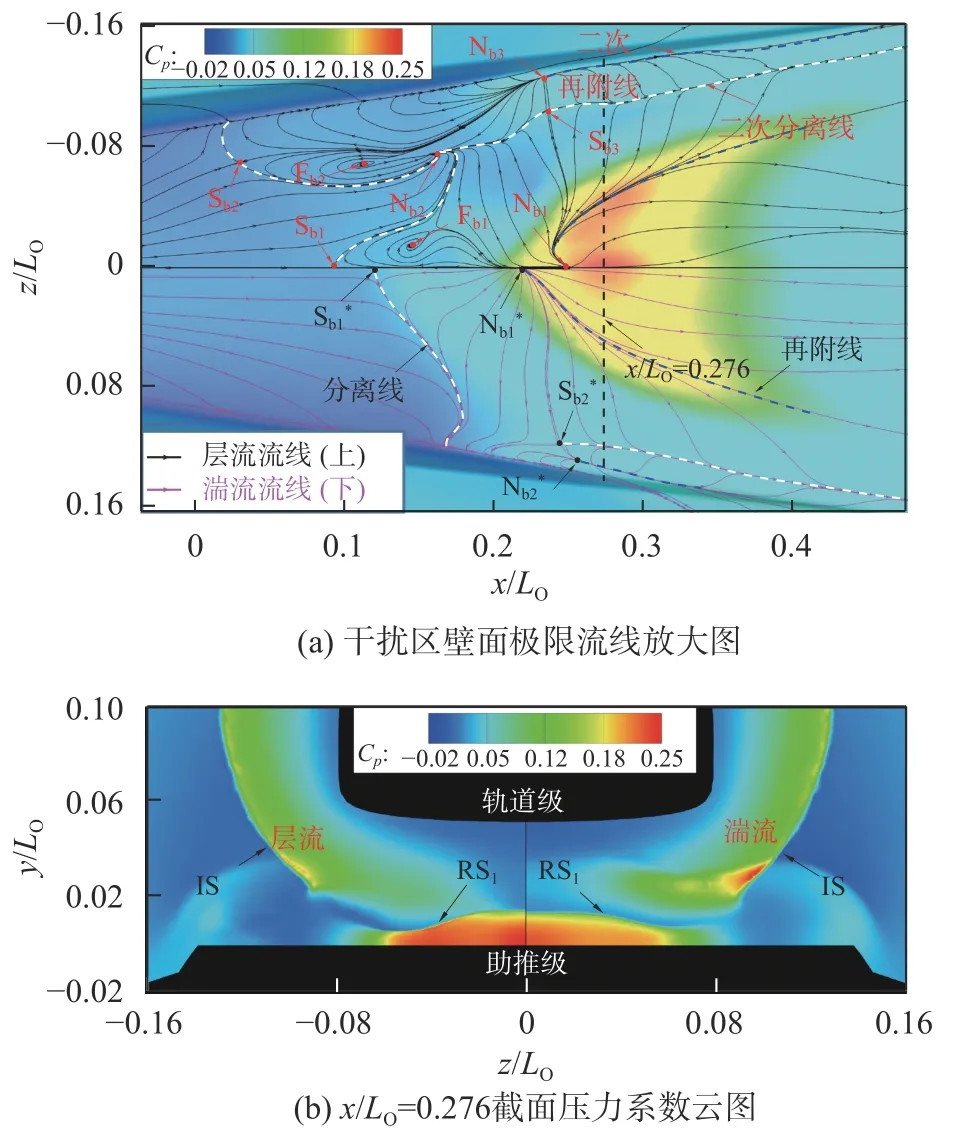
圖10 激波IS 入射助推級上壁面形成的干擾區流場Fig. 10 Flow fields induced by the impingement of shock wave IS on the upper booster wall

首先，由于層流邊界層抵抗逆壓梯度的能力較弱，在強的入射激波IS 作用下，大尺度流動分離產生，形成中心線上x/LO=0.092處的分離鞍點Sb1和x/LO=0.248處的再附結點Nb1。其次，由于激波IS 的三維特性，高壓區在展向向下游移動且壓力值逐漸降低，致使分離線在展向快速彎曲；同時來流沿分離線的流動偏轉及分離區內的逆向流動共同作用，導致了順時針螺旋圍繞焦點Fb1的“龍卷風”旋渦結構（tornado-like vortex[26]）形成。另外，在靠近助推級凸起平臺的邊緣處，平臺下方氣流進入平臺時發生卷曲，形成了順時針旋轉的源于結點Nb3的渦結構；該旋渦與來流相向運動產生的剪切作用產生了焦點為Fb2的逆時針旋轉“龍卷風”旋渦結構，相鄰的兩個旋渦將分離線推向上游并以兩者之間的鞍點Sb2-結點Nb3連線為漸進收斂邊界；中心區域與邊緣的分離線在結點Nb2處交匯并發生轉折；而源于結點Nb1的再附線在展向向下游延伸，與高壓區輪廓相似。此外，平臺外側產生的壓縮波（如圖10（b）所示）在平臺邊緣形成展向逆壓梯度，進而引起展向的流動分離，形成流經結點Nb2和鞍點Sb3的沿流向方向的二次分離線，以及源于結點Nb3的二次再附線。而湍流干擾流場則相對簡單，湍流邊界層抵抗逆壓梯度能力較強，中心線上的分離鞍點Sb1*和再附結點Nb1*相對層流狀態向內收縮，分別位于x/LO=0.121和x/LO=0.219處；同樣的，在助推級凸起平臺的邊緣處也有因下方氣流上洗帶來的旋渦以及展向壓力梯度引起的二次流動分離，但是尺度都相對較小；沿流向方向的二次分離線與再附線分別流經鞍點Sb2*和結點Nb2*。由于湍流分離區尺度較小，來流與分離區逆向流動之間的剪切較弱，沒有形成焦點以及“龍卷風”旋渦結構。

圖11（a）給出了軌道級在反射激波RS1作用下的干擾區壁面流場。圖中鞍點S、結點N 和焦點F 的下標“o”表示位于軌道級上；同樣的，上標“*”代表湍流結果。圖11（b）則顯示了干擾區壁面中心線最大壓力系數處（x/LO=0.471，在圖11（a）用黑色虛線標示）橫截面的壓力系數云圖。反射激波RS1入射軌道級下壁面引起的高壓區也呈弧狀向下游展開；在x/LO=0.471截面可以看到未作用到軌道級壁面、向空間發展的激波RS1以及在軌道級壁面反射形成的激波RS2；激波RS2波面在展向也逐漸靠近壁面，并且強度呈遞減趨勢，層流狀態壓力系數在展向的下降速率要高于湍流狀態，進而導致高壓區在展向持續距離較短。

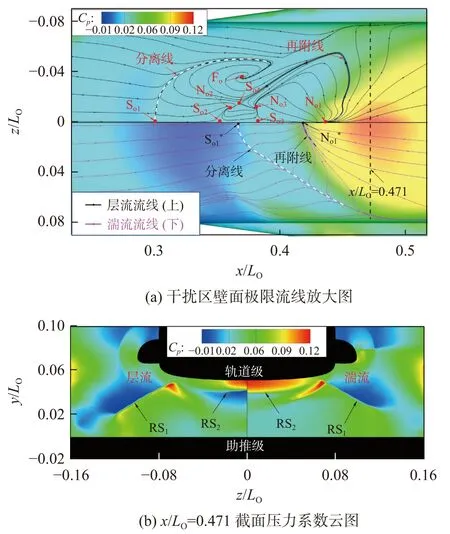
圖11 激波RS1 入射軌道級下壁面形成的干擾區流場Fig. 11 Flow fields induced by the impingement of shock wave IS1 on the lower orbiter wall

軌道級壁面邊界層受激波RS1作用引起的分離區明顯也是開放的，層流狀態的干擾流場也相對復雜且范圍較大。中心線上的分離鞍點So1和再附結點No1分別位于x/LO=0.300和x/LO=0.430處。在軌道級邊緣與分離區內，帶展向方向的相對流動導致了展向分離線的彎曲以及焦點位于Fo處的“龍卷風”旋渦的產生，進而在分離區內形成位于中心線的鞍點So2和So3，以及展向并列的結點No2和No3。隨后，源于結點No1、No2、No3的流線在鞍點So4處漸進收斂，進而將中心分離區劃分為三個部分；在鞍點So2-So4和結點No2-No3圍成的區域內，產生向下游的流動，方向與其余兩部分分離區相反。而對于湍流狀態，流動分離起始點大幅后移，分離區的流動結構也相對簡單，只有中心線上的分離鞍點So1*和再附結點No1*分別位于x/LO=0.366和x/LO=0.418處，以及經過兩點并在展向發生彎曲的分離線和再附線，沒有出現其他的鞍點、結點以及焦點等臨界點。

圖12 給出了RS1下游其余反射激波（RS2~RS4）作用在助推級和軌道級壁面的極限流線圖，并用黑色虛線標示出圖7 所示激波引起的壁面中心線壓力峰值的位置，在未發生流動分離時可認為是激波入射點。

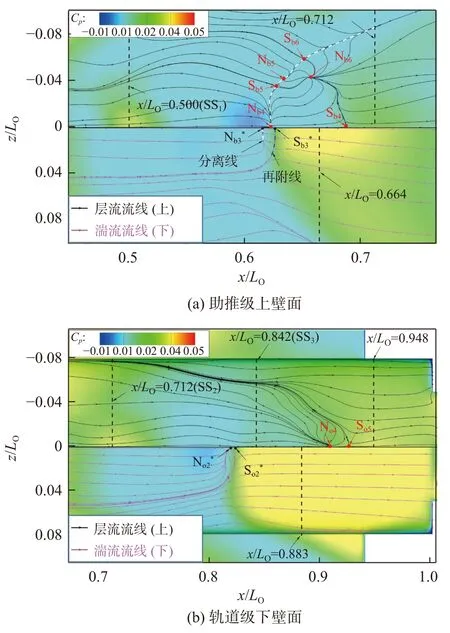
圖12 激波RS1 下游壁面流場Fig. 12 Flow structures downstream of shock wave RS1

隨著激波在級間的來回反射，激波/邊界層干擾強度依次遞減。對于助推級，激波SS1沒有引起層流邊界層發生分離，而激波RS2則導致層流和湍流狀態均發生流動分離。其中，層流狀態中心線分離結點Nb4和再附鞍點Sb4分別位于x/LO=0.622和x/LO=0.687處，由Nb4發展的分離線呈彎曲狀，依次經過鞍點Sb5、結點Nb5以及鞍點Sb6，而再附線則終止于結點Nb6處。此時，激波RS2在助推級壁面產生的干擾強度和范圍均遠小于激波IS 的作用，其中心線分離區長度只有后者的42%左右。湍流狀態的分離區中心線起始位置分別位于結點Nb3*（x/LO=0.615）和鞍點Sb3*（x/LO=0.626）處，并且在展向的持續距離也很短，流動分離帶來的影響較弱。相應地，激波SS2和SS3也沒有引起軌道級層流邊界層發生分離，而激波RS3產生的層流和湍流狀態的流動分離尺度都很小，特別是湍流狀態，分離結點N02*（x/LO=0.819）和鞍點S02*（x/LO=0.823）非常接近，分離對流動帶來的影響非常弱。

2.4 空間流動特征

圖13 給出了激波IS 干擾區的級間空間流場結構及流線，其中對稱面和x/LO=0.276橫截面展示馬赫數云圖，模型壁面展示壓力梯度。

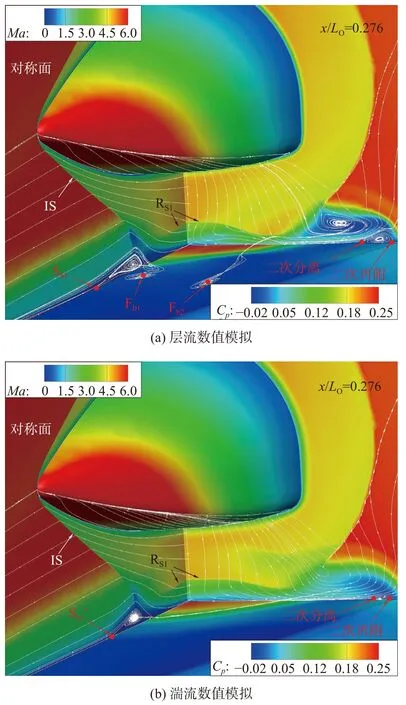
圖13 激波IS 作用干擾區的空間流場Fig. 13 Three-dimensional flow fields in the interference area induced by the impingement of shock wave IS

從對稱面分離泡向展向空間發展的流線可以看出，分離泡在空間上也不再是封閉形式。其中，層流對稱面分離泡內有流向相鄰焦點Fb1的氣流，因此該處的“龍卷風”旋渦流動方向是從空間螺旋卷向壁面；而源于焦點Fb2的空間流線則是由壁面螺旋上升并隨主流向下游流動。另外，湍流對稱面分離泡內向展向逃逸的氣流則直接隨主流向下游流動。助推級近壁區域的橫向流動在平臺邊緣處受到逆壓梯度的影響，發生流動分離；明顯地，層流狀態的這種二次分離尺度要大于湍流狀態，并且層流較大的流動分離還導致其上方產生空間旋渦結構。

圖14 給出了激波RS1干擾區的級間空間流場結構及流線，選擇x/LO=0.471處橫截面展示橫向流動。由于層流的分離區較大，導致對稱面上的分離激波SS1以及與RS1之間的干擾都明顯強于湍流狀態；同時，層流對稱面的分離區內存在對應于壁面鞍點So2和So3的兩個旋轉中心；壁面焦點Fo匯聚有包括來流、對稱面分離區靠近上游的旋轉中心以及再附結點的空間流線，并且呈螺旋狀流向壁面；湍流對稱面分離區內也有橫向流出并隨主流向下游傳播的氣流。另外，在x/LO=0.471橫截面，軌道級近壁區域氣流也由于展向的順壓梯度產生橫向流動，但沒有在展向形成流動分離。

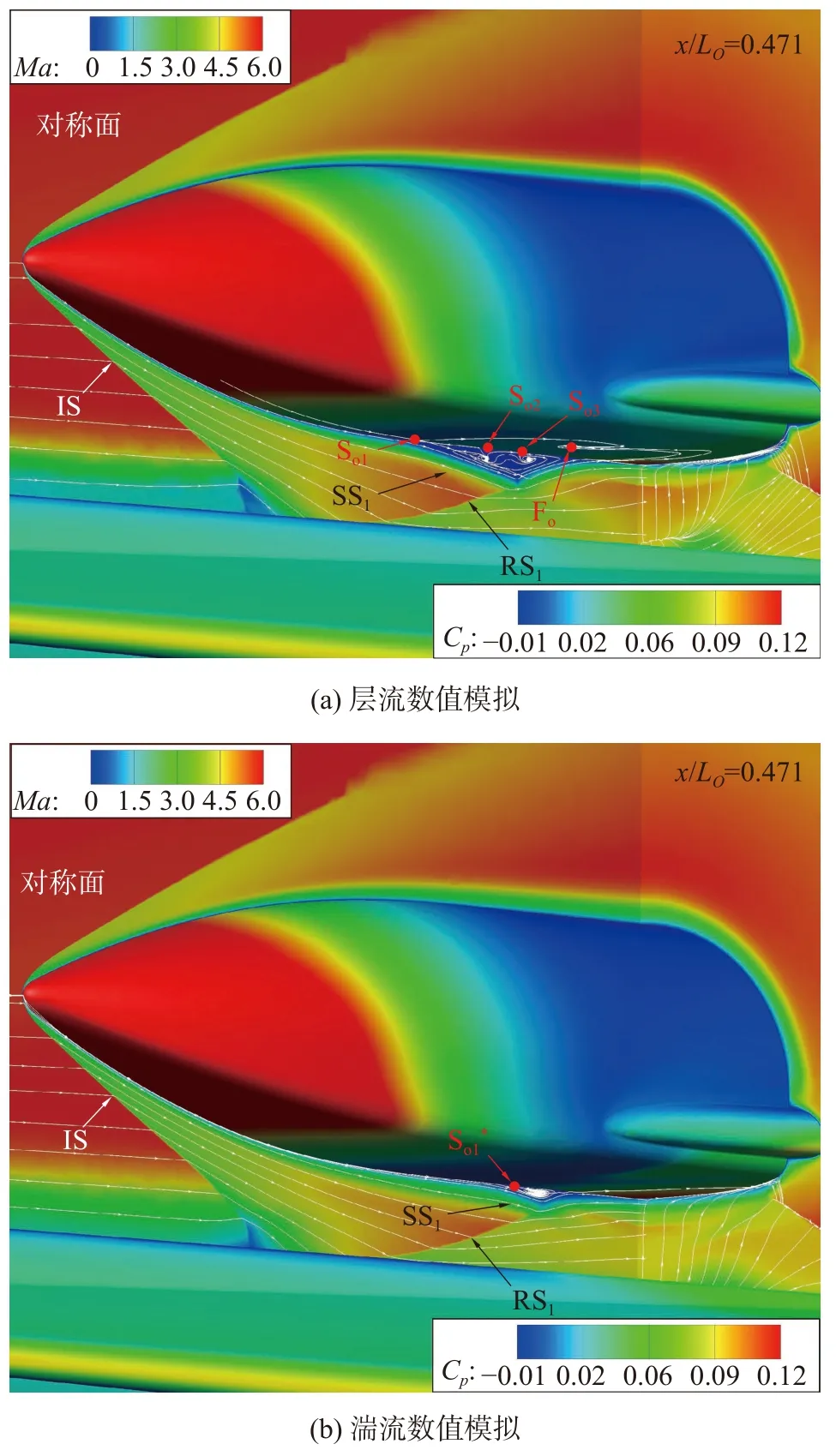
圖14 激波RS1 作用干擾區的空間流場Fig. 14 Three-dimensional flow fields in the interference area induced by the impingement of shock wave RS1

3 結 論

針對TSTO 標模縮比模型，通過紋影、NPLS、壁面靜壓測量以及油流圖像等多種試驗技術，結合層流與湍流的數值模擬手段，獲取了馬赫數6 條件下的助推級與軌道級典型級間激波/邊界層干擾流場流動圖譜與壓力分布，并展示了壁面干擾結構與空間流場之間的相關性。通過分析得到以下結論：

1）試驗中，助推級與軌道級模型壁面邊界層在激波入射之前均保持為層流狀態，激波引起層流邊界層分離的同時增強了流動的不穩定性，導致強干擾后的再附邊界層迅速轉捩為湍流狀態，因此試驗結果在第一道激波的作用結束之前與層流計算結果吻合，而在激波作用之后，與湍流計算結果一致。

2）激波/邊界層干擾呈現復雜的三維流動特征，軌道級頭部貼體激波入射至助推級上壁面形成的高壓區呈弧狀向下游展開，隨后激波在級間來回反射并且激波/邊界層干擾強度依次遞減；同時，干擾區內存在顯著的橫向流動，主分離線與再附線也在展向發生彎曲變形；分離區不再是起止于分離線和再附線的封閉結構，而是向空間發展并隨主流向下游傳播，伴隨上游氣流從側向匯入，分離區呈明顯的開放結構。此外，展向的壓力梯度導致在助推級上壁面平臺邊緣處發生流動分離，形成沿流向排列的二次分離線與再附線。

3）由于層流邊界層抵抗逆壓梯度的能力較弱，其受到相同激波作用形成的干擾區明顯大于湍流狀態，同時流動結構更為復雜，開放特征也更為顯著。在強干擾區內壁面上存在包括鞍點、結點、焦點在內的臨界點以及有旋渦結構的流動特征；且源于焦點的“龍卷風”旋渦，其流動方向既可能從壁面螺旋上升，也可能從空間螺旋卷向壁面。

4）對于TSTO 標模級間三維激波/邊界層干擾引起的大尺度流動分離與旋渦結構，其非定常特性將是級間可控分離所關注的另一焦點問題，后續將開展深入研究。

致謝：感謝中國航天空氣動力技術研究院沈清、陳蘭、胡靜等在TSTO 標模多體分離特性研究中的支持，感謝中國科學技術大學李祝飛關于本文研究內容的有益討論。