翼傘后緣偏轉過程的流固耦合動力學特性

高興龍，陳 欽，*，張青斌，李志輝

(1. 中國空氣動力研究與發展中心，綿陽 621000；2. 國防科技大學 空天科學學院，長沙 410073)

0 引 言

翼傘是一種雙層結構的柔性矩形翼，上、下翼面用翼型的肋幅分隔成若干氣室，翼型前緣開口，在前進飛行中形成“沖壓空氣”，維持若干個氣室的內壓以保持翼型[1]。當翼傘系統需要進行機動轉彎和雀降等操縱動作時，會對翼型后緣進行下拉偏轉操作來實現。

翼傘后緣偏轉的操縱過程會顯著改變翼面的整體氣動布局，同時需要多根操縱繩精確協同控制，是典型的氣動與結構緊耦合問題，涉及到的動力學問題復雜多變。對于翼傘系統操縱過程的動力學機理問題研究一直是降落傘領域的關鍵技術和熱點問題。著名的美國X-38 太空成員返回飛行器利用翼傘后緣下偏進行減速著陸的操縱，成功實現了太空人員返回安全著陸，是迄今為止世界上最大最先進的翼傘研究項目[2]。除此之外，比較典型的應用案例有美國研制的聯合精確空投系統（joint precision airdrop system,JPADS），該系統是一個高空、全天候、GPS 制導的精確空投系統，包括超輕型和輕型兩種布局，前后兩者的最大載重量分別約為998 kg 和4536 kg，空投精度優于50～100 m。其他案例還有加拿大的“雪雁”（SnowGoose）偵察系統和“夏爾巴人”（Sherpa）精確空投系統、歐洲的SLG-Sys 自主滑翔傘降系統等[2]。

目前對于翼傘后緣偏轉的動力學行為研究主要依靠數值仿真和試驗，其中數值仿真主要采用流固耦合仿真技術對沖壓翼傘動力學行為進行預測。目前國內外專門針對翼傘流固耦合過程的動力學機理研究已經逐漸由傳統的完全試驗法、半試驗半理論法和完全理論法三種手段，轉向了基于先進CFD 和CSD 方法的大規模并行數值仿真技術。Tang 等[3]基于LS-DYNA 軟件中的ICFD 流體求解器和結構求解器仿真計算了翼傘后緣下偏過程的結構變形行為。Tezduyar 所領導的團隊基于DSD/SST 有限元方法開展了沖壓翼傘系統的流固耦合計算仿真[4]。Fogell等[5]基于松耦合、利用CFD 和CSD 方法對翼傘穩態飛行的充氣外形進行流固耦合仿真，研究了翼傘結構變形和周圍的流場特性。Altmann[6]使用勢流理論和簡化有限元法分析了翼傘的流固耦合問題。近年來，國內專門針對翼傘系統的流固耦合研究也逐漸增多，Nie 和Cao[7]基于Dirchlet/Neumann 迭代方法研究了翼傘充氣過程的流固耦合問題，騰海山團隊[8,9]基于LS-DYNA 求解器對翼傘穩態構型進行了流固耦合仿真，同時對大型翼傘操縱轉彎過程的氣動特性進行仿真分析。汪龍芳等[10]基于索膜有限元模型和CFD 方法對翼傘穩態飛行的氣動變形進行了三維數值模擬，并分析了氣室的“鼓包”現象。孫青林等[11-12]研究了襟翼偏轉過程翼傘系統的氣動性能變化。郭一鳴等[13]基于松耦合方法和參數辨識開展了翼傘變形和下偏情況的動力學和氣動性能仿真。但是針對翼傘后緣下偏過程的氣動與結構耦合動力學特性研究較少，本文分別考慮翼傘后緣偏轉過程的非線性氣動特性和結構響應行為，采用數值仿真與試驗對比的方法深入分析了翼傘單側和雙側后緣偏轉過程的流固耦合動力學特性。

本文基于Structured ALE（S-ALE）流固耦合方法對翼傘后緣偏轉過程進行動力學建模和仿真分析。研究翼傘三維模型后緣偏轉過程、傘衣結構場和周圍流場的時變演化規律及分布特性，為進一步指導大型翼傘精確空投系統的飛控系統設計和技術應用提供參考。

1 流固耦合建模

1.1 問題描述及假設

本文所研究的翼傘后緣偏轉過程是針對充滿鼓包狀態的翼傘三維模型進行的。翼傘系統包括傘衣、傘繩和掛重載荷，幾何模型如圖1 所示。實際流固耦合仿真過程只考慮傘衣結構與流場的雙向耦合作用；傘繩在翼傘偏轉過程承受拉力，且通過傘繩施加后緣下拉過程的作用力載荷；忽略傘繩與周圍流體的耦合作用和繩索的阻尼效應。

1.2 結構動力學

翼傘傘衣為柔性織物結構，一般由透氣量極低的抗撕錦絲綢材料制成，本文忽略傘衣織物結構的透氣量，則結構域的控制方程可以表示為[14]：

其中，ρs為材料密度，u為結構質點的速度矢量，σs為柯氏應力張量，fs為作用在結構的外部力， ?s代表結構域的速度邊界。

1.3 流體動力學

翼傘系統周圍流體域的動力學方程為[15]：

其中，ρf、uf分別為密度和速度矢量，ff和 σf分別為外部力和應力張量， ?f代表流體域的速度邊界。通過引入ALE 格式，網格可以自由移動。在參考構型下不可壓縮流的ALE 格式控制方程為：

其中，流體速度uf=v-w，v和w分別為參考構型下的流體質點速度和材料網格點速度，g是單位密度的外力矢量。 當v=w時，公式為拉格朗日形式；當v≠w時，公式為歐拉格式。同時給出Dirichlet 和Neuman形式的邊界條件如下：

其中，n是法向矢量，h為流固耦合邊界接觸力矢量。

1.4 罰函數法

在翼傘系統的整個后緣偏轉過程中，傘衣結構變形與周圍流場變化相互作用，通過流固耦合界面信息的傳遞保證相互作用過程的能量守恒。通常有限元模型很難實現流體和結構網格的完全匹配，本文基于歐拉-拉格朗日描述下的罰函數法進行流體與傘衣結構間節點力信息的傳遞，該方法允許非匹配的流體和結構網格[16]。

流固耦合界面為傘衣織物結構表面，罰函數的穿透力fc計算公式為：

其中，ks代表罰函數的剛度系數；m為積分時間步；dm代表結構節點在第m個時間步進入流體域的穿透深度，與結構和流場網格節點的相對運動速度有關，可以在積分過程進行迭代計算。

利用穿透深度和相對運動速度可以在每個時間步內判斷穿透是否發生，若穿透發生則在流固耦合界面上對流場和結構網格節點施加大小相等、方向相反的作用力，以滿足流固耦合界面的受力平衡：

假設流體為滲透性介質，采用顯式動力學積分方法對仿真模型進行迭代計算，從而完成流固耦合信息的關聯和傳遞。

2 仿真方法驗證

首先針對翼傘氣室單元后緣偏轉過程進行仿真計算，初步驗證本文所采用方法的計算收斂性和可行性。建立翼傘氣室結構的三維有限元模型，并在后緣沿操縱繩方向施加下拉載荷。流場域完全包裹結構模型，流場網格采用結構化網格。為避免因流體和結構單元之間尺寸差異過大而導致顯式動力學積分過程可能出現的非物理特征“沙漏現象”，進而引起計算發散，流場網格尺寸與結構網格尺寸盡量接近1∶1，如圖2 所示。

圖2 翼傘氣室流固耦合仿真網格模型Fig. 2 Mesh model of the parafoil cell for the FSI simulation

本文采用S-ALE 求解方法對流固耦合模型進行仿真計算，S-ALE 方法與傳統ALE 方法的基本理論相同，均包括了映射過程的對流輸運、界面重構和歐拉流場與拉格朗日結構相互作用的流固耦合過程[17]。不同的是，在網格的處理方法上，S-ALE 方法采用自動生成網格技術，即流場網格根據控制點設定的方向、增長率、網格尺寸、網格密度等參數在仿真過程中隨著時間步的推進逐漸產生，仿真前無需單獨建立流場網格。這可以極大減小網格處理時間并提高計算效率。經過仿真測算，與傳統ALE 方法相比，S-ALE 方法的計算效率可以提高60%[18]。

計算的來流速度為15 m/s，來流攻角為0°，流場和結構域的計算結果如圖3～圖5 所示。

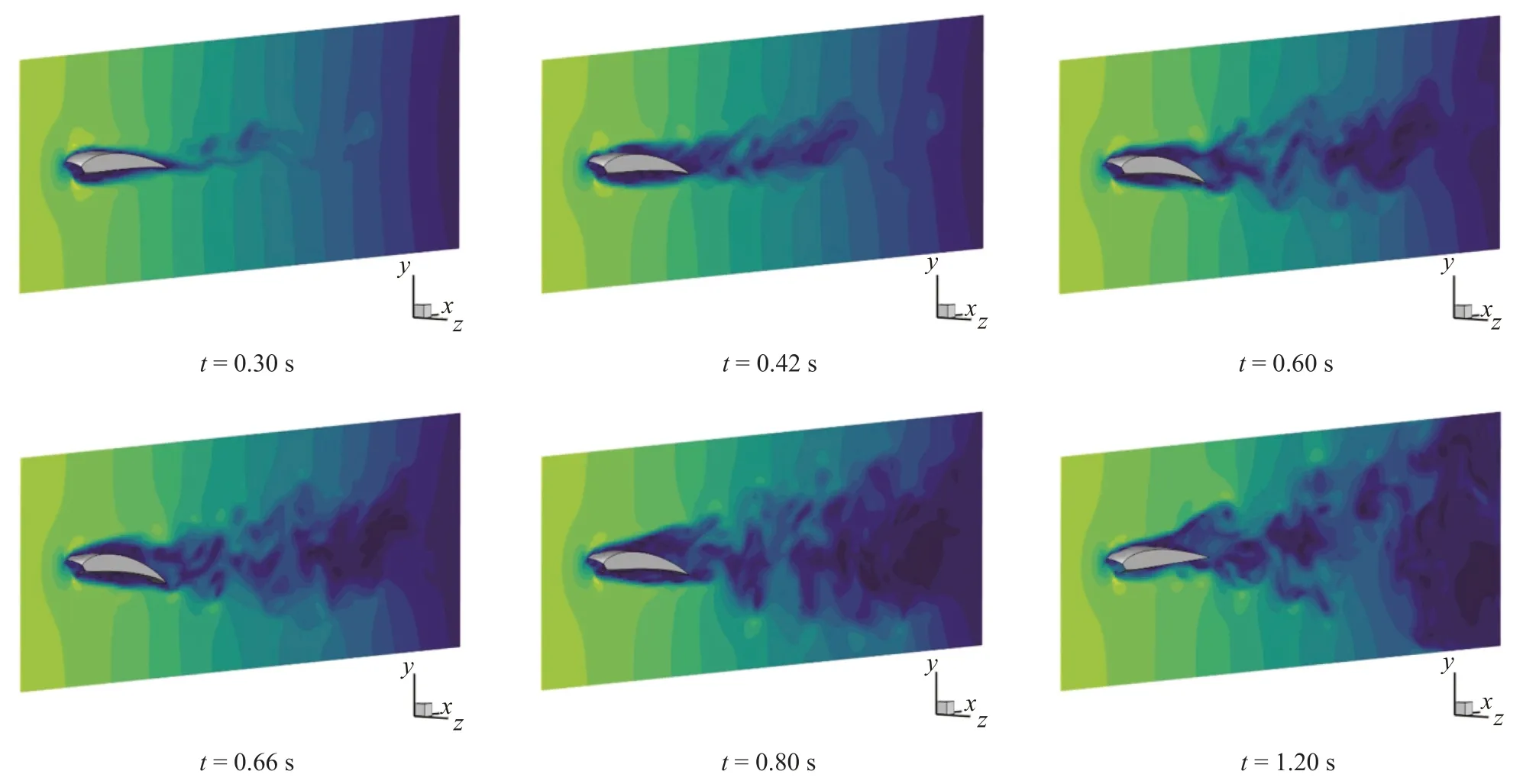
圖3 翼傘氣室后緣偏轉過程流場速度變化云圖Fig. 3 Velocity contour variations of the parafoil cell under trailing-edge deflection

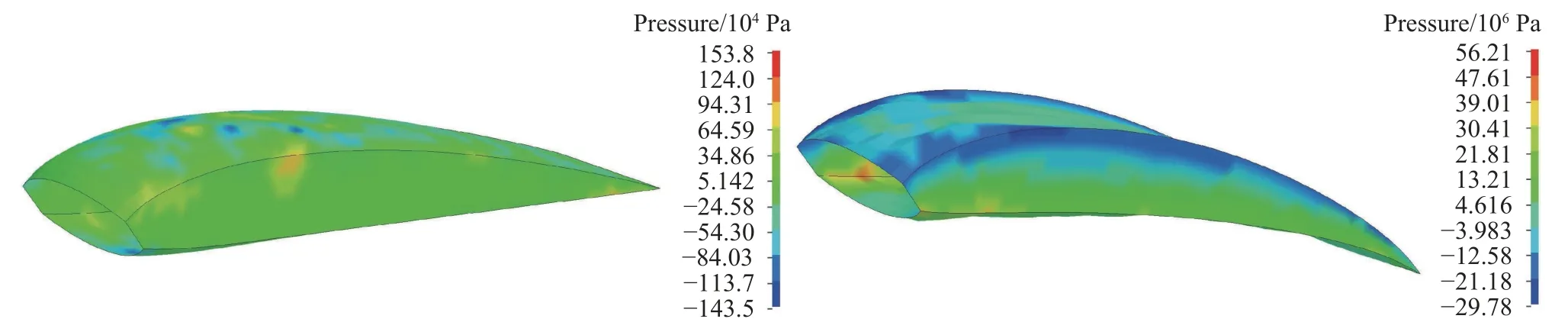
圖5 翼傘氣室后緣偏轉過程傘衣表面壓力分布云圖Fig. 5 Pressure contours of the parafoil cell under trailing-edge deflection

從圖3 流場演化結果中的速度云圖可以明顯看到渦流由上翼面向后緣逐漸過渡和破碎的過程。隨著后緣向下偏轉程度的增大，在后緣尾部的上端出現明顯的低速區域，形成高壓的逆壓梯度，從而引起流動分離現象。從圖4 和圖5 的傘衣結構應力和壓力分布云圖中可以看出，氣室中間鼓包區域為受力較為集中且強度高的區域。

將采用本文流固耦合方法仿真計算得到的下偏狀態翼傘氣室單元結構有限元模型導出，作為幾何邊界模型，采用Fluent 對該導出的后緣偏轉氣室單元進行氣動特性仿真計算驗證，來流速度同樣取為15 m/s，湍流模型選擇標準k-ω模型，計算得到的翼傘氣室單元后緣下偏狀態翼型表面的壓力系數為0.65。采用本文流固耦合仿真方法計算得到的同樣狀態翼型表面壓力系數為0.62。兩種方法的結果較為接近，初步驗證了本文方法的有效性和可靠性。

3 仿真結果與驗證

翼傘氣室單元仿真計算初步驗證了本文方法的可行性和收斂性，將本文方法進一步應用于整個翼傘系統多氣室后緣偏轉過程的流固耦合仿真。為了模擬翼傘機動轉彎和雀降著陸兩個經典操縱動作，分別對整個翼傘系統模型的后緣單側下偏和雙側下偏過程進行仿真計算。

3.1 流固耦合結果

圖6 和圖7 為翼傘后緣單側和雙側下偏操縱過程的傘衣表面結構Von Mises 應力分布云圖。從圖中可以明顯看出傘衣的上翼面整體應力分布較為均勻，但當后緣下偏時，在偏轉與未偏轉的轉折交接區域會出面明顯的應力集中且受力增大；同時翼型前緣也相應出現類似現象，且與后緣應力集中區域的受力水平接近。說明翼傘后緣偏轉發生的轉折交接區域和偏轉側前緣切口區域是在翼傘操縱過程比較容易發生撕裂現象的區域，應考慮在這兩處增加結構強度。從傘衣結構受力水平來講，在下偏量相同的情況下，雙側下偏的傘衣結構受力明顯高于單側下偏情況。

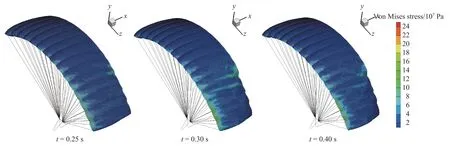
圖6 不同時刻單側下偏傘衣表面結構Von Mises 應力云圖Fig. 6 Von Mises stress contours of the canopy under single deflection at different time instances

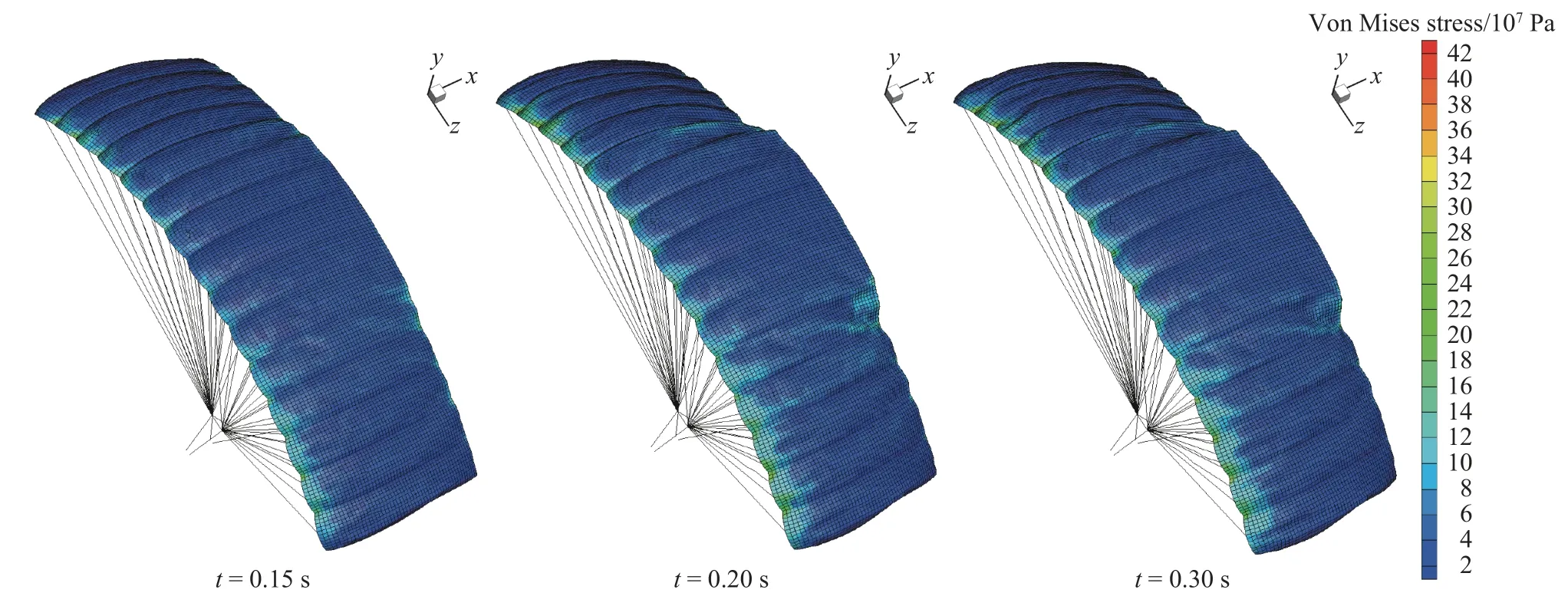
圖7 不同時刻雙側下偏傘衣表面結構Von Mises 應力云圖Fig. 7 Von Mises stress contours of the canopy under double deflection at different time instances

圖8 和圖9 為翼傘后緣雙側下偏過程不同時刻的傘衣周圍流場速度變化云圖。從單側下偏過程的速度變化分布云圖可以看出，在翼傘的尾緣頂部緊貼上翼面附近出現近似圓形的高速區域，當下偏時該區域被拉長，下偏完成后此區域減小。該高速區域會使上翼面頂部的氣流自后緣向前緣倒流，產生流動分離，這也是翼傘轉彎操縱出現失穩現象的主要原因。從雙側下偏過程的橫向剖面流場速度分布云圖可以看出，該高速區域主要存在于翼傘下偏發生的轉折交界區域附近。

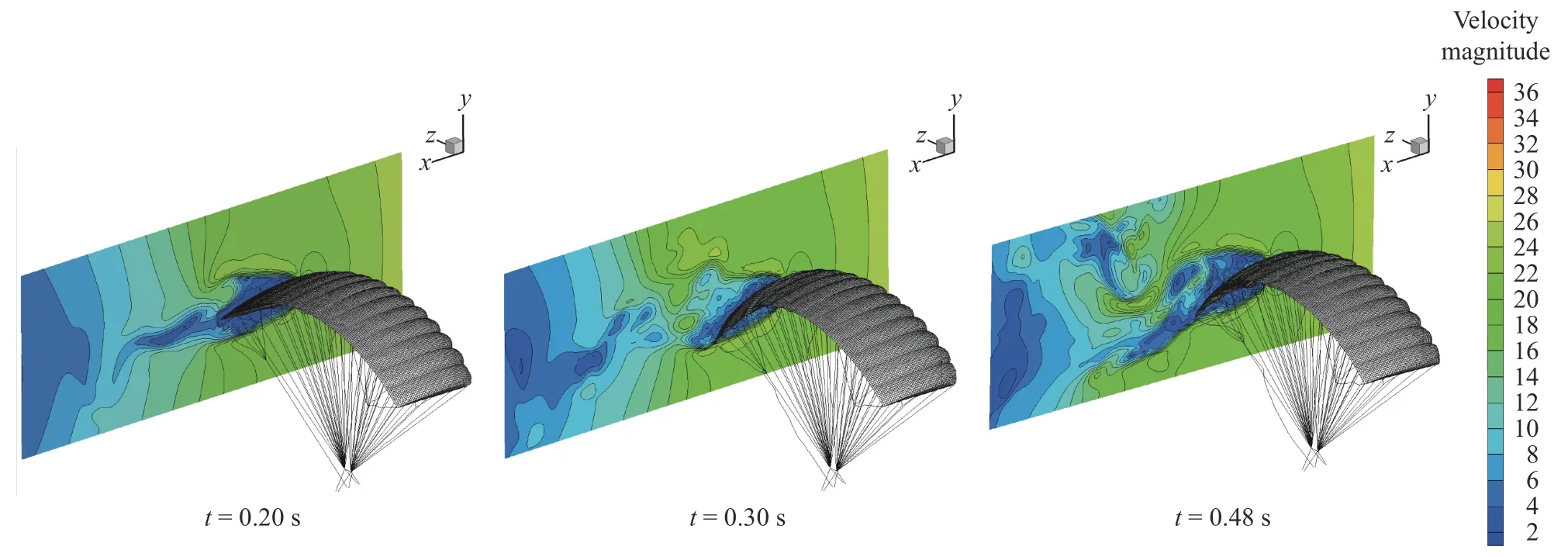
圖8 不同時刻單側下偏傘衣周圍流場速度變化云圖Fig. 8 Velocity contours around the canopy under single deflection at different time instances

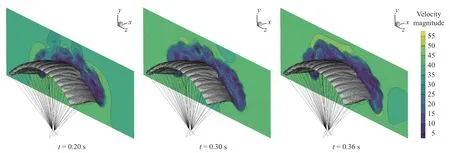
圖9 不同時刻雙側下偏過程周圍流場速度變化云圖Fig. 9 Velocity contours around the canopy under double deflection at different time instances

3.2 性能曲線結果

圖10 為翼傘后緣單側和雙側下偏過程所施加的下偏量隨時間的變化曲線。兩種情況的下偏量相同。圖11～圖13 分別為兩種情況的翼傘氣動阻力面積、升力系數、阻力系數三者隨時間變化曲線。后緣單側下偏對應翼傘的操縱轉彎動作，下拉量開始時間為0.2 s，此時升力系數出現一個峰值，下偏量達到最大的時刻為0.3 s，此時阻力系數最大，阻力面積的變化與下偏量變化結果趨勢較為一致。

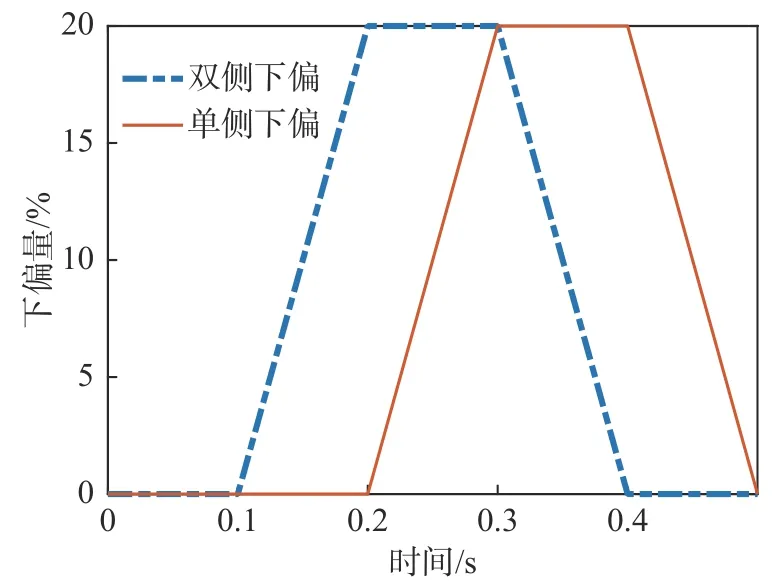
圖10 翼傘后緣下偏過程下偏量隨時間變化Fig. 10 Time variation of the deflection for the parafoil under trailing-edge deflection

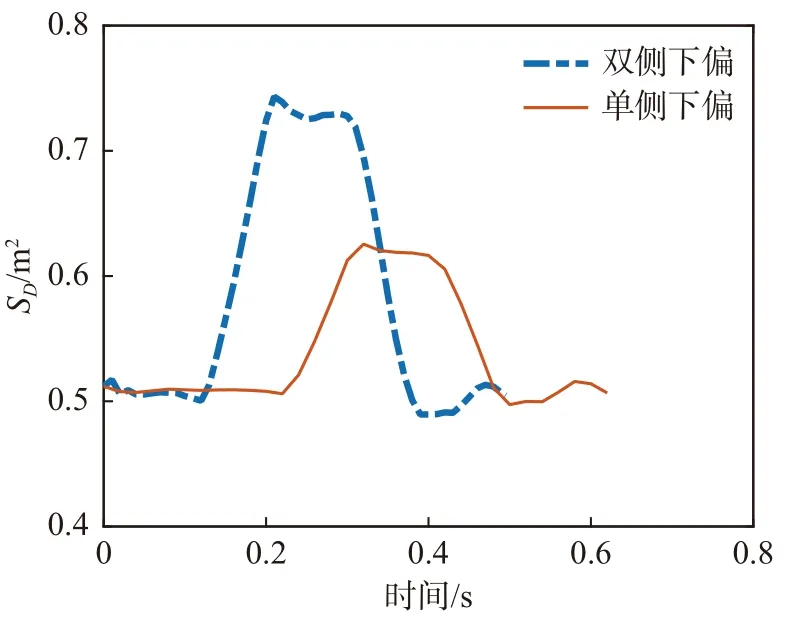
圖11 翼傘后緣下偏過程氣動阻力面積隨時間變化Fig. 11 Time variation of the drag area for the parafoil under trailing-edge deflection

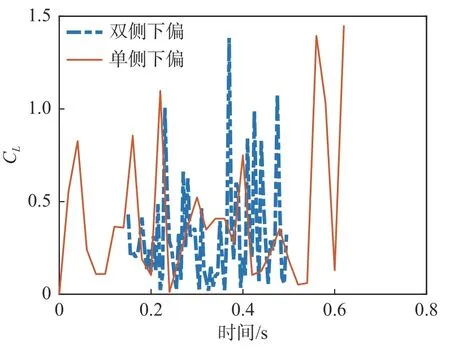
圖12 翼傘后緣下偏過程氣動升力系數隨時間變化Fig. 12 Time variation of the lift coefficient of the parafoil under trailing-edge deflection

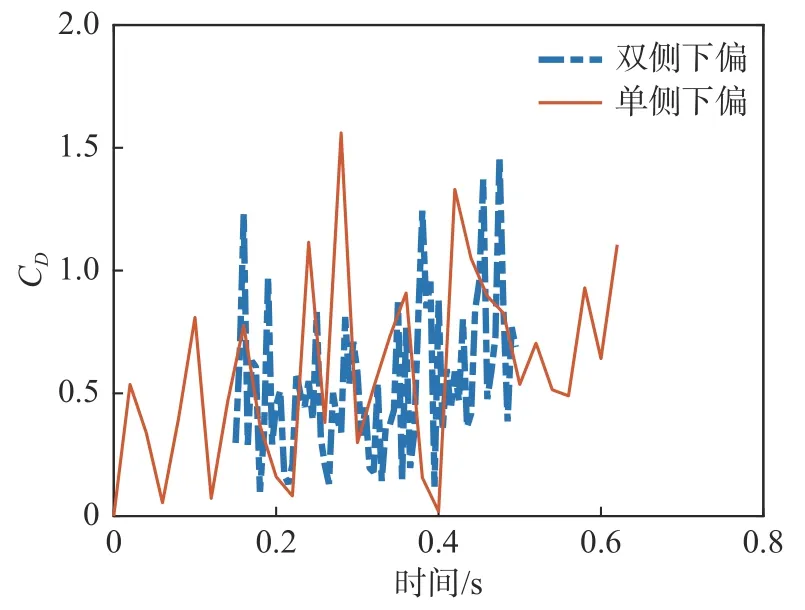
圖13 翼傘后緣下偏過程氣動阻力系數隨時間變化Fig. 13 Time variation of the drag coefficient of the parafoil under trailing-edge deflection

雙側下偏過程對應翼傘的雀降著陸操縱動作，翼傘下偏量達到最大的時刻為0.2 s，但翼傘最大阻力系數出現的時間約為0.44 s，最大升力系數出現的時間約為0.38 s，均晚于下拉操縱量達到最大的時刻，表明沖壓翼傘后緣雙側下偏操縱過程具有延遲響應的特性。

3.3 試驗驗證

為進一步驗證本文仿真結果，將流固耦合仿真計算獲得的后緣雙側下偏過程達到不同下偏量的翼傘系統結構有限元模型輸出保存，利用ANSYS 軟件將有限元模型轉換為翼傘結構外輪廓的實體幾何模型，并采用3D 打印技術打印出實體模型。

在0.55 m×0.4 m 低噪聲航空聲學風洞對翼傘模型進行靜態測壓吹風試驗，風速同樣為15 m/s。在翼傘每個氣室的翼型模型中剖面布置一定數量的測壓孔，對測得的壓力分布在升力方向積分，得到該狀態翼傘系統的升力系數。

表1 為翼傘后緣偏轉模型升力系數仿真與試驗的對比結果，其中仿真結果為利用本文方法對不同下偏量的翼傘結構外輪廓模型進行的流固耦合仿真。從對比可以看出仿真結果與試驗結果較為一致，且不同下偏量對應的升力系數變化趨勢相同。

表1 翼傘后緣偏轉模型升力系數對比結果Table 1 Lift coefficient comparison of the parafoil under trailing-edge deflection

4 結 論

本文研究了翼傘后緣下偏過程的流固耦合動力學問題。在單個氣室翼型的后緣偏轉過程仿真研究中發現偏轉過程氣室周圍流場出現分離流動現象。之后對整個翼傘的后緣下偏過程進行流固耦合仿真，并利用風洞試驗對仿真結果進行驗證，研究結果表明基于S-ALE 和罰函數法的流固耦合技術可以進行翼傘后緣偏轉過程的流固耦合動力學行為研究：1）傘衣結構計算結果表明后緣下偏過程應力集中區域位于翼型前緣切口和后緣下偏轉折發生區域；2）通過分析氣動參數的時間歷程演化趨勢，發現沖壓翼傘的后緣下偏過程會出現明顯的延遲響應現象。總之，利用本文所采用的流固耦合方法可以對翼傘空投系統的氣動結構耦合動力學行為進行較好的預測，有助于翼傘精確空投系統的技術驗證和設計分析。