基于數值模擬的飛機近場尾渦特征參數計算

溫瑞英，李鵬柯，劉 聰，王紅勇

(中國民航大學 空中交通管理學院，天津 300300)

0 引 言

尾流是飛行過程中飛機上下翼面壓力差導致氣流從機翼后緣脫落形成的一對反向旋轉的尾渦，有空間尺度大、旋轉切向速度高、持續時間久等特點。尾渦流場的存在會影響后續飛機的飛行姿態，甚至引發飛行事故，國際民航組織制定了尾流間隔標準來預防尾流造成的飛行事故。隨著航空工業的發展，航班流量不斷增加，機場容量的提升成為航空運輸發展中迫切需要解決的問題。但尾流間隔過大將限制機場容量增加，因此建立尾流間隔預測系統，合理地縮減尾流間隔是提高機場容量、緩解航空壓力的關鍵。在這樣的現實背景下，對飛機尾流的研究在近年來得到了不斷發展和完善。

基于計算流體動力學的數值模擬方法是研究飛機尾流的主要手段之一[1]。尾渦在機翼后緣的延伸距離長達十幾公里，在計算條件限制下使用數值模擬方法對尾流的研究主要分為近場和遠場兩方面。

在近場方面，國內外研究者采用不同的數值模擬方法對翼尖渦的形成及尾渦近場演變進行了大量研究。Chow 等[2]基于雷諾平均N-S 法（RANS）模擬了NACA0012 機翼翼尖渦的形成和近場演化過程，發現翼尖渦近場卷起為湍流運動，且強度隨流向距離迅速衰減。Morton 等[3]基于RANS 和分離渦法（DES）對三角翼的近場尾渦進行研究，發現大迎角條件下DES 模擬結果與實驗數據更擬合。Jiang 等[4]基于大渦模擬（LES）研究近場尾渦的形成過程，分析了翼尖渦脫落轉變為穩定近場尾流的原因。劉薇等[5]基于RANS 對 NACA0012 機翼近場尾渦進行模擬，發現在采用六面體網格的數值模擬中，RKE 模型得到的結果與風洞實驗值更吻合。溫瑞英等[6]基于RANS 對B757-200 飛機的近場尾渦特性進行數值模擬，研究了飛機近場尾渦的演化特征。艾國遠等[7]基于LES研究不同雷諾數對翼尖渦的層流分離流動機制的影響。林孟達等[8]基于LES 研究飛機尾渦在大氣中的演變特性，對尾渦近場卷起過程采用升力面尾渦生成法，結果表明該方法可減少網格量，提高計算效率。

在遠場方面，國內外研究者主要研究氣象條件對尾渦消散的影響和尾渦的近地演化規律。Han 等[9]基于LES 研究了大氣湍流與飛機尾流的關系，發現尾流的壽命會受到周圍大氣湍流的顯著影響。Proctor 等[10]基于LES 對飛機尾流的地面效應進行研究，發現尾渦在距地面高度低于0.6 倍初始渦間距時，其強度受到地面效應的影響而急劇下降。Stephan等[11]基于LES 研究地面加設障礙物對飛機尾流的影響，發現合理地布置地面障礙物可以加快尾渦的消散。Xu 等[12]基于LES 研究了跑道設置吹氣或吸氣區對尾流消散的影響，結果發現吹氣區附近產生的分離渦對尾流的消散有著明顯的影響。魏志強等[13]基于RANS 方法對尾渦在側風條件下的演化進行了研究，發現水平方向上高強度的側風能加速尾渦的消散。上述研究均采用簡化尾渦速度模型對近場尾渦進行初始化，該方法在一定程度上忽略了近場尾渦對尾渦后續演化及其衰減的影響。

目前關于模擬飛機尾渦完整生命周期的研究較少，對尾渦近場和遠場的獨立研究無法準確地展示尾渦的整體演化規律。由于尾渦的生命周期長，因此可采用近遠場耦合的多段法進行全流場尾渦數值模擬，在保證計算結果高精度的同時，避免計算量和計算條件的限制。本文基于尾流數值模擬現狀，對A320 飛機的近場尾渦進行了數值計算，研究了飛機近場尾渦特征參數的計算方式，并利用Hallock-Burnham（H-B）和Lamb-Oseen（L-O）模型對尾渦流場進行反演，驗證了尾渦特征參數計算方法的有效性。基于飛機近場尾渦所提取的特征參數可以作為遠場尾渦演化和消散機制研究的基礎。

1 飛機尾渦數值模擬方法

1.1 幾何模型與網格劃分

本文采用A320 飛機的機翼作為計算模型，具體的計算外形和網格分布圖如圖1 所示，模型具體尺寸見表1。

表1 A320 機翼數據Table 1 Wing parameters of A320

三維機翼模型的坐標原點取機翼最前緣點，氣流流動方向為z軸負方向，沿展向指向左翼為x軸正方向，機翼面上方垂直于氣流流動的方向為y軸正方向。

計算區域設置為：機翼上方取3cr，機翼下方取5cr，機翼左右側各取3cr，機翼前方取4cr，機翼后方取25cr。

為了獲得較高的網格精度和質量，計算網格采用結構化六面體網格。為了提高網格的正交性，機翼周圍的網格采用自適應O 型網格進行劃分。經過反復試算與調整，綜合考慮計算需求和計算配置，最終計算域網格分布為Nx×Ny×Nz= 270 × 120 × 420，總網格數為1.4018×107。

1.2 數值模擬方法與邊界條件

1.2.1 數值模擬方法

本文計算在天河1 號超級計算機上完成。采用RANS 方法捕捉飛機尾渦的形成并逐漸卷起的過程，利用有限體積法進行求解。雷諾平均法求解的雷諾方程如下：

式中： 〈〉為系綜平均，ui表示雷諾平均速度分量，xi和xj(i,j= 1, 2, 3) 表示三個方向的坐標，υ為運動黏度，p為壓強，fi為質量力，ρ為流體密度。

1.2.2 邊界條件設置

計算域的翼展方向、飛行方向、頂部和底部的邊界均設為壓力遠場，飛機機翼表面設為無滑移壁面。

根據A320 型飛機進場和離場速度，來流速度為67 m/s，飛行馬赫數為0.2，飛行迎角為10°，大氣壓力為104103.1 Pa。

2 飛機尾渦特征參數計算方法

尾渦的壽命一般分為近場渦與遠場渦兩個階段，其中，近場渦可分為卷起區和成熟區兩部分，遠場渦可分為中遠場和消散區兩部分[14]，尾渦壽命階段分布如圖2 所示。

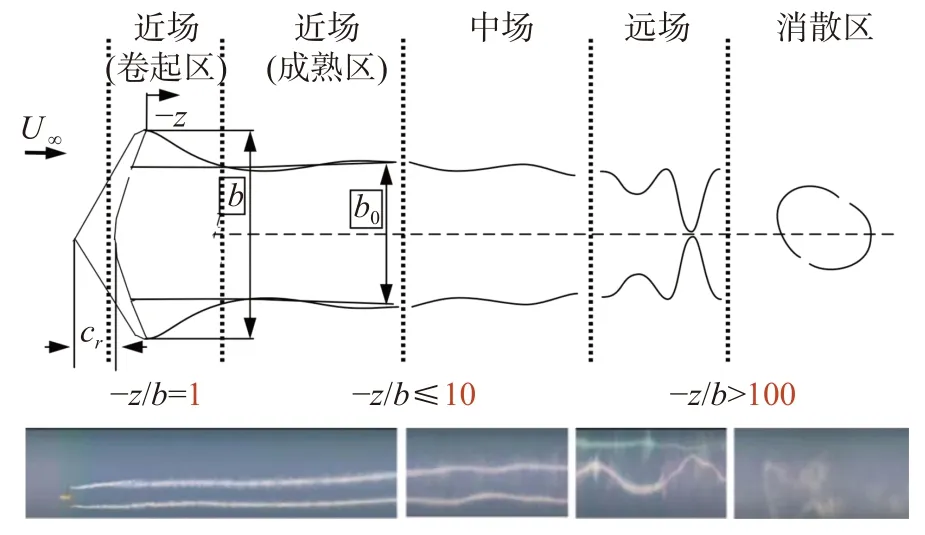
圖2 尾渦壽命各階段示意圖Fig. 2 Temporal evolution of wake vortices

一般認為沿機翼后緣延伸10 倍翼展長度內的區域為近場渦區域。其中，從機翼后緣脫落的渦面卷起形成高度集中的渦旋的過程為卷起區，擁有成型渦核且渦柱穩定的階段為成熟區。圖3 通過三維軸向渦量等值線圖展示了A320 機翼在7 個翼展內的近場尾渦演化過程，可以看出近場尾渦分為兩個區域：1 倍翼展（?z/b= 1）內為卷起區，該區域內渦核剛開始成形；?z/b= 2～7 為成熟區，是尾渦逐漸穩定乃至成熟的過程。圖4 為?z/b= 2 內的渦量等值線圖，可以看出當尾渦流向距離為?z/b= 1 時渦核開始卷起。

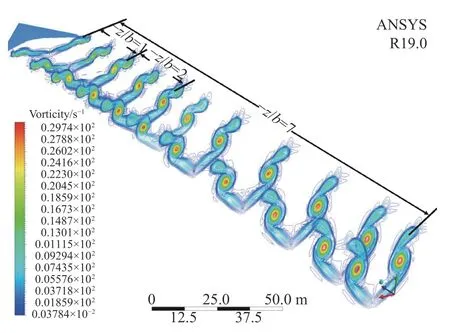
圖3 A320 飛機的近場尾渦Fig. 3 Near-field wake vortices of A320

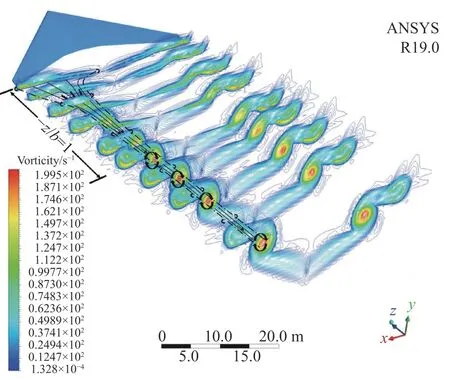
圖4 近場尾渦卷起過程Fig. 4 The lift up of near-field wake vortices

在描述飛機尾渦基本特性時，采用相對于基準參數的無量綱標稱參數。本文采用以下兩個基準參數簡化計算，即初始尾渦環量Γ0和初始尾渦間距B0：

式中：ny為飛機的法向過載；W為飛機重量；ρ為飛行高度上的空氣密度；V∞為飛機飛行速度；b為機翼的翼展。

2.1 渦核位置和渦核間距

飛機的尾渦可以簡化成兩個旋轉方向相反的渦旋，渦旋中心存在一個渦核。渦量是描述尾渦運動的一個矢量[15]，本文通過尋找渦量最大值的方法來確定渦核的位置，其中渦量ω的表達式見式（4）：

式中：ωx=?w/?y??v/?z為x軸渦量分量，ωy=?u/?z??w/?x為y軸渦量分量，ωz=?v/?x??u/?y為z軸渦量分量，u、v和w分別為沿x、y和z方向的速度分量。

通過最大渦量值確定左右渦核位置后，兩渦核之間的距離即渦核間距B。

2.2 渦核半徑

尾渦的旋轉特性可以用切向速度來描述。尾渦的切向速度Vθ計算公式如下：

z軸方向速度分量相對于x軸和y軸方向的數值較小，因此在切向速度的計算中忽略不計。

渦核半徑為渦核位置與最大切向速度位置之間的長度[6,16,17]，文獻中僅考慮切向速度最大的點，這種由單個值計算的渦核半徑存在一定偏差，因此本文采用平均值的方法來計算渦核半徑。

2.2.1 平均正圓法

平均正圓法是以最大切向速度值劃分出包含多個點的速度范圍，將多個點距離渦核位置的長度取平均值作為渦核半徑，如圖5 所示為左渦渦核計算示意圖，具體方法為：

圖5 平均正圓法計算渦核半徑Fig. 5 The average circle method computing vortex radius

1）為避免右渦速度場對左渦的影響，以左渦核為原點，選取以渦核為圓心，半徑不超過翼展四分之一的圓為計算域；

2）在計算域內找到切向速度值最大的點，并找到滿足與最大切向速度值相差在0.2 m/s 內的所有點；

3）計算上述所有點與渦核之間的距離，將其平均值定義為渦核半徑。

2.2.2 平均橢圓法

圖6 給出了?z/b= 7 截面處左渦面的切向速度分布圖，其渦核形狀接近橢圓，因此本文提出如圖7 所示的平均橢圓法來確定渦核半徑，以左渦為例，具體方法為：

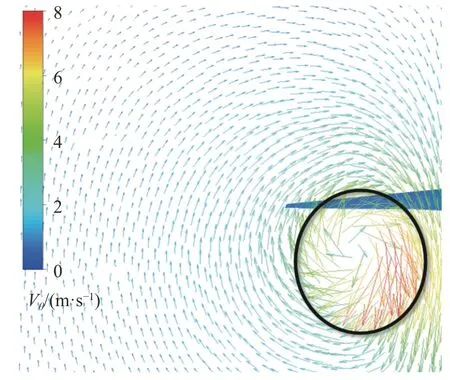
圖6 ?z /b = 7 截面尾渦切向速度矢量圖Fig. 6 Tangential velocity of the wake vortex at ?z /b = 7

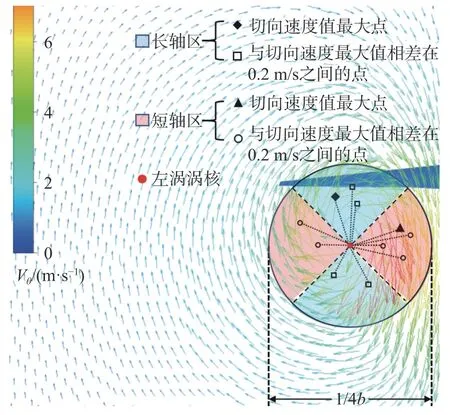
圖7 平均橢圓法計算渦核半徑Fig. 7 The average ellipse method computing vortex radius

1）以左渦核為原點，選取半徑不超過翼展的四分之一的圓為計算域；

2）渦核的垂直方向定義為y軸，與y軸夾角為?45°～+45°、?135°～+135°之間的區域設為長軸區，在長軸區內找到切向速度最大的點，并找到滿足與最大值相差0.2 m/s 的所有點，將其與渦核之間的距離平均值定義為長軸半徑；

3）同理，將渦核的水平方向定義為x軸，與x軸夾角為?45°～+45°、 ?135°～+135°之間的區域設為短軸區，與長軸做法相同得到短軸半徑；

4）將長軸半徑和短軸半徑的平均值定義為渦核半徑。

2.3 尾渦環量

尾渦強度一般用環量來表征，環量是流體速度沿一條封閉曲線路徑的線積分。根據切向速度剖面計算尾渦環量，如式（6）：

式中：Γ(r)為距渦核徑向距離為r處的尾渦環量；Vθ(r)為距渦核徑向距離為r處的切向速度。

由于尾渦剖面內各點切向速度不同，因此常用平均環量，即對一個半徑區間內的環量取平均值來表示尾渦強度，計算公式見式（7）：

式中，rl≤ri≤ru，rl為半徑區間的下限，ru為半徑區間的上限。

文獻[18,19]通過激光雷達測量了飛機的尾渦數據，對尾渦環量的計算方法進行了評估。由于激光雷達不能捕獲尾渦的細微結構，尤其是渦核附近的流場區域，因此文獻[18,19]采用Γ5?15作為大型飛機（翼展約為60 m）尾渦強度計算的環量平均值，公式見式（8），式中半徑間隔以1 m 為增量計算：

對于翼展為b的飛機模型，文獻[19]給出計算尾渦環量的半徑區間為b/12～b/4。

通過數值模擬可以得到尾渦整個流場的細微結構，本文通過分析中型客機A320 的近場尾渦環量隨渦核徑向距離的變化規律，探討計算尾渦環量時更合適的半徑區間。采用尾渦環量的平均絕對誤差MAE 對半徑區間選取的合理性進行評價，MAE 的計算見式（9）：

圖8 給出了A320 飛機?z/b= 2～7 的尾渦截面上左渦無量綱環量值Γ?（Γ?=Γ/Γ0）隨渦核徑向距離的變化規律。可知當渦核徑向距離小于5 m 時，無量綱尾渦環量隨徑向距離的增加而急劇增大，在渦核徑向距離5～11 m 之間，環量值隨徑向距離增加而緩慢增加，在11 m 處到達峰值后開始緩慢下降。

圖8 無量綱尾渦環量隨渦核徑向距離的變化規律Fig. 8 The evolution of dimensionless circulation with the radial distance

1）半徑區間下限rl的確定。此處采用固定半徑上限、逐步增大半徑下限的方式進行討論，將b/2 向上取整作為半徑區間的上限值，以1 m 為單位增大半徑下限。圖9 給出了MAE 值隨半徑下限值增大的變化規律，可以看出2 倍翼展截面的MAE 值最大，因為該截面上的尾渦剛卷起，速度特征不明顯，而流向距離較遠截面處的MAE 值較低。半徑下限值小于3 m時，MAE 值隨著下限值的增大而減小；半徑下限值在4～10 m 之間時，MAE 值呈增大趨勢；半徑下限大于10 m 后，MAE 值開始減小。在半徑下限取值為3 時MAE 值為極小值，因此半徑下限的最優值為3 m，即rl= 3。

圖9 MAE 值隨半徑下限值的變化規律Fig. 9 Variations of MAE with the lower bound of radius

2）區間上限ru的確定。將半徑區間的下限rl=3 設為定值，對半徑區間的上限進行討論。為避免左右渦之間的相互干擾對尾渦環量計算精度的影響，以b/2 向上取整作為半徑上限[16]。圖10 反映了MAE值隨半徑上限值增大的變化規律。由圖可知，在半徑區間上限值小于10 m 時，MAE 值隨半徑上限值的增大而急劇減小；半徑上限值在10～12 m 之間時MAE值緩慢減小；在半徑上限值大于12 m 時，MAE 值基本保持不變。因此半徑上限的最優值可取為12 m，即ru= 12。

圖10 MAE 隨半徑上限值的變化規律Fig. 10 Variations of MAE with the upper bound of radius

結合圖8 可知，渦核徑向距離在3～12 m 之間時，環量值變化趨勢平緩；低于3 m 時，環量值過低會使得MAE 值增大；高于12 m 時，環量值變化不明顯，且由圖10 可知增加了不必要的計算。綜合可得，計算尾渦環量平均值的最佳半徑區間可選為3～12 m。

圖11 給出了不同半徑區間尾渦平均環量的MAE 值隨尾渦流向距離的變化規律。可以看出，Γ3?12得到的MAE 值低于Γ5?15和Γ3?9（根據b/12～b/4可得出A320 飛機計算尾渦環量平均值的半徑區間為3～9 m）。因此基于數值模擬得出的近場尾渦，采用Γ3?12描述渦面環量分布更加準確。

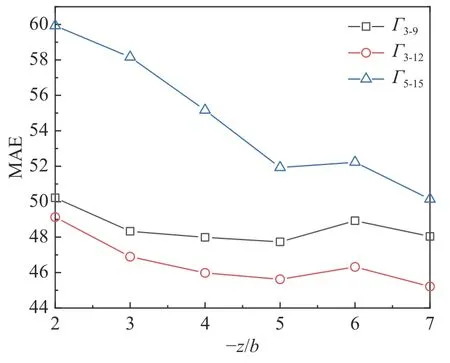
圖11 不同半徑區間MAE 值隨流向距離的變化Fig. 11 Streamwise variations of MAE in different radius

2.4 尾渦特征參數計算方法驗證分析

為了驗證本文尾渦特征參數計算方法的精準度，采用H-B 和L-O 模型對尾渦流場進行驗證，具體做法如下：

1）根據L-O 和H-B 的速度模型，推導出流場任意點處的速度計算公式，通過計算的渦核位置、尾渦環量和渦核半徑得出一個反演速度場。

2）將反演速度場與數值模擬計算得到的尾渦速度場進行對比，對尾渦參數計算方法的準確性進行評估。

2.4.1 速度場的構建

假設尾渦流場中一個截面的左右渦核位置坐標分別為(x1,y1)和 (x2,y2)，其中左渦渦核半徑為rc1、環量為Γ1，右渦渦核半徑為rc2、環量為Γ2。流場中任意一點的坐標為(x,y)，該點距離左渦渦核的長度為r1，距離右渦渦核的長度為r2。圖12 為兩個點渦所計算的流場任意點(x,y)處展向和垂直方向上的速度分量。

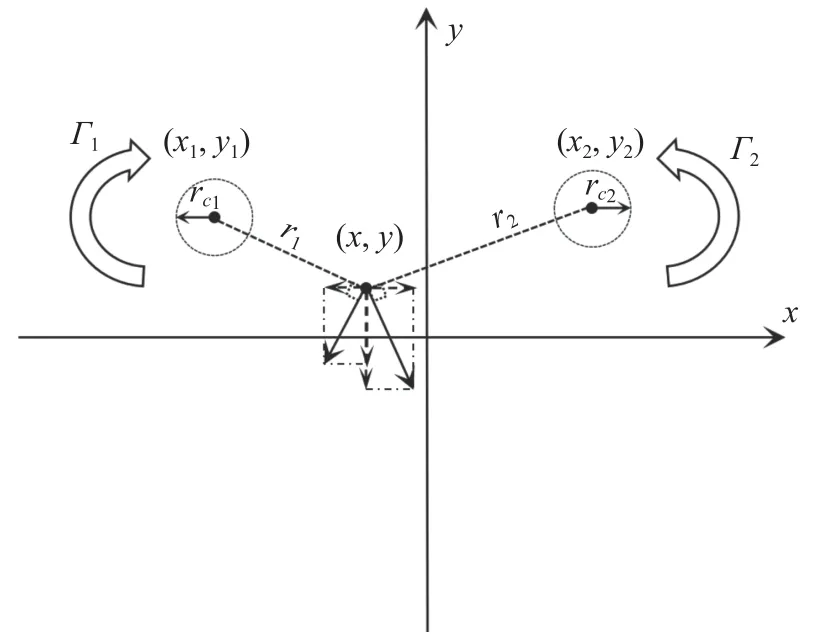
圖12 速度分量計算示意圖Fig. 12 The calculation of velocity components

Hallock-Burnhan 模型簡稱H-B 模型，該模型的單點渦速度公式如式（10）：

基于H-B 模型，計算流場任意點(x,y)處切向速度的展向速度分量Vx和垂直速度分量Vy，如式（11）、式（12）：

Lamb-Oseen 模型簡稱L-O 模型。該模型的單點渦速度公式如式（13）：

基于L-O 模型，計算流場任意點(x,y)處切向速度的展向速度分量Vx和垂直速度分量Vy，如式（14）、式（15）：

2.4.2 速度場誤差分析

為了反映反演速度場與數值模擬速度場之間的誤差，本文選用均方根誤差（RMSE）對結果進行評價，計算公式見式（16）：

式中：Vxi、Vyi分別是反演速度場中任意一點的展向速度分量和垂直速度分量；ui、vi分別是數值模擬速度場中任意一點處的展向速度分量和垂直方向速度分量。

選取流向距離-z/cr=3.5、4、4.5、5、8、10、13、16、19、21、25，共11 個截面進行計算分析。

圖13 為采用平均正圓法和平均橢圓法計算渦核半徑時，速度場RMSE 值隨流向距離的變化規律，其中選取3～12 m 的環量平均值作為尾渦環量。由圖可知：當流向距離在?z/cr= 3.5～10 之間，兩種計算方法得到的RMSE 值基本一致，且RMSE 值隨著流向距離增加而急劇減小；當流向距離在?z/cr= 10～25之間，各方法得到的RMSE 值隨流向距離增加而緩慢減小，且平均橢圓法的RMSE 值更低。說明采取平均橢圓法計算渦核半徑更加精確。

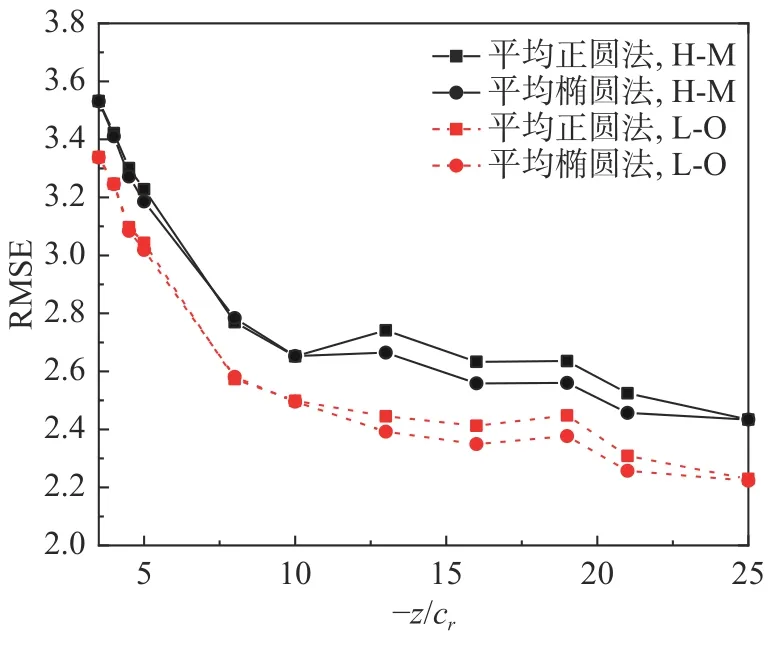
圖13 不同渦核半徑計算方法下RMSE 隨流向距離的變化Fig. 13 Streamwise variations of RMSE obtained by different methods of computing rc

圖14 為采用不同半徑區間計算環量平均值時，RMSE 值隨流向距離的變化規律，其中渦核半徑的計算方法為平均橢圓法。由圖可知： RMSE 值隨流向距離的增大而減小；對比三種半徑區間，Γ3?12得到的RMSE 值最小。說明采用Γ3?12作為近場尾渦環量平均值更加精確。

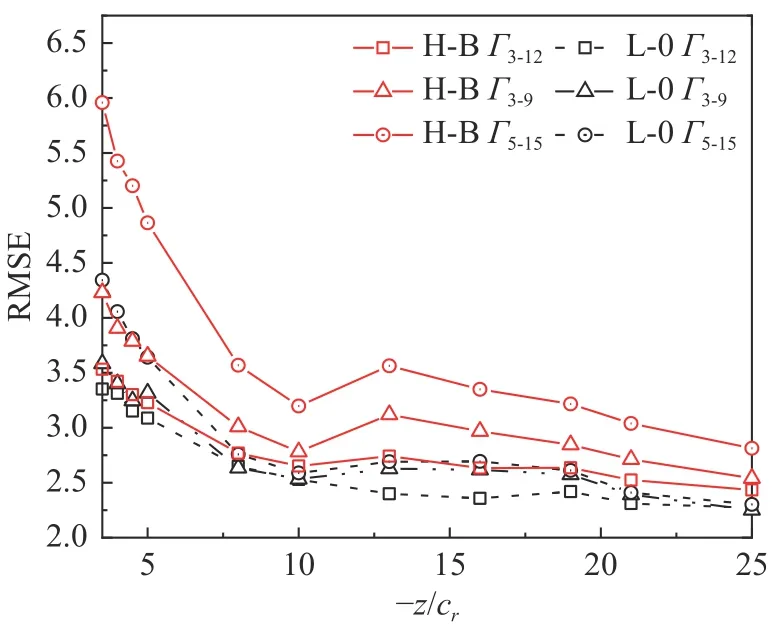
圖14 不同半徑區間下RMSE 隨流向距離的變化Fig. 14 Streamwise variations of RMSE at different radius intervals

由圖13、圖14 可知，整個近場中，在不同半徑區間和不同渦核半徑計算方法下，L-O 模型的RMSE 值均低于H-B 模型。因此，采用L-O 模型描述近場尾渦的速度分布時，擬合度更高。

3 飛機近場尾渦計算結果及分析

1）渦核位置。圖15 為渦核位置所在的橫向坐標隨流向距離的變化規律。可以看出：在流向距離?z/cr= 5，即一倍翼展之后，左右渦核位置的橫向坐標隨著流向距離的增加而逐漸減小。

圖15 渦核橫向坐標隨流向距離的變化Fig. 15 Streamwise variations of the lateral coordinates of vortex cores

圖16 為渦核位置的縱向坐標隨流向距離的變化規律。可以看出：左右渦的變化曲線重合，即下落趨勢一致。隨著尾渦流向距離的增加，左右渦核在流向距離?z/cr= 5 之后開始逐漸向下移動。

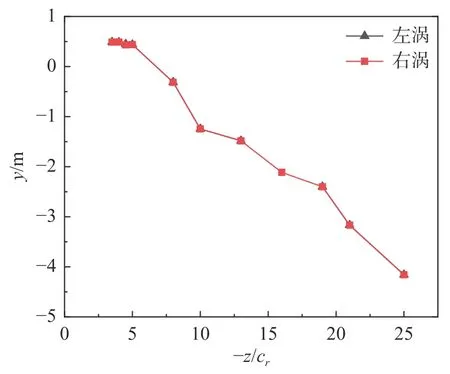
圖16 渦核縱向坐標隨流向距離的變化規律Fig. 16 Streamwise variations of the vertical coordinates of vortex cores

圖17 無量綱渦核間距隨流向距離的變化規律Fig. 17 Streamwise variation of the dimensionless distance between vortex cores

3）渦核半徑。圖18 為無量綱化左渦渦核半徑隨流向距離的變化規律。可以看出：在流向距離小于?z/cr= 10 時，渦核半徑隨著流向距離的增加而增加；流向距離在?z/cr= 10～16 之間，渦核半徑小幅度減小；流向距離在?z/cr= 16 之后，渦核半徑隨著流向距離的增加而急劇增大。在近場尾渦區域，使用平均橢圓法計算得到的渦核半徑值小于平均正圓法。

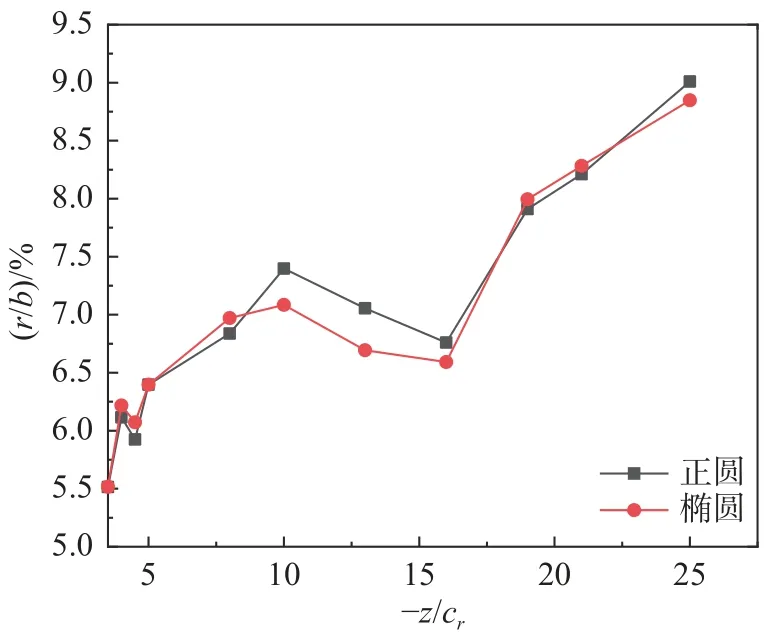
圖18 無量綱左渦核半徑隨流向距離的變化規律Fig. 18 Streamwise variation of the dimensionless radius of the left vortex core

4 結 論

本文基于RANS 數值模擬方法，模擬了A320 機翼的近場尾渦演化過程，對其近場尾渦流場特征參數的計算方法進行了分析，主要結論如下：

1）對于數值模擬的A320 近場尾渦，采用平均橢圓法計算渦核半徑，精度更高；作為特征參數進行尾渦速度場構建，擬合度更好。

2）通過對比尾渦截面的環量誤差和速度場誤差，發現對于數值模擬的A320 近場尾渦，在計算尾渦環量時，采取3～12 m 的半徑區間作為平均值更好，常用的5～15 m 的半徑區間并不適用于中型客機的尾渦環量值估算。

3）對比了H-B 和L-O 模型，以數值模擬得到的近場特征參數進行尾渦速度場的構建擬合，發現LO 模型在近場成熟區構建的速度場與原速度場的誤差更小，擬合程度更好。