非線性Caputo-Hadamard型分數階微分包含正解的存在性
馬玉花,顧海波,李 寧
(新疆師范大學數學科學學院,新疆 烏魯木齊 830017)
分數階微積分是應用數學中最重要的領域之一,它將現有的整數階的微分算子推廣到任意階的微分算子。近年來,關于分數階微分方程問題引起了人們廣泛的關注。分數階微分方程應用于反常擴散、流體力學、生物醫學、最優控制等領域。相比起整數階的微分算子,分數階微分算子具有全局性,從而可以準確描述客觀世界的發展規律。
伴隨著自然科學及社會科學發展、復雜工程應用需求的增加,分數階微分方程已不能滿足人類探索發展規律的需求,而微分包含可以看作是分數階微分方程的推廣,它可以對復雜的現象進行更加準確的刻畫。對于微分包含解的存在性一直是人們研究的熱點問題,同時人們已經不再滿足去尋找微分包含的一般解,而是想找到更具有現實意義的正解。有關分數階微分包含的理論研究有很多[1-13]。在現有的成果當中,有關分數階微分包含正解的存在性定理的結果并不是很多[8-9],因此,對于微分包含具有多個正解的存在性研究是必要的。
文[6]中,作者結合變分方法和臨界點理論,給出了下面一類帶奇異項的非局部問題正解的唯一性。
其中Ω是RN(N≥3)是一個有界開區域且具有光滑邊界階?Ω,a,b≥0且a+b>0,m>0,λ≥0,1 文[7]中,作者利用不動點定理,給出了下面一類非線性加權問題正解的存在性。 文[8]中,作者通過多值映射的壓縮不動點定理,給出了下面非線性分數階微分包含正解的存在性定理。 受以上結果的啟發,本文將研究如下帶有積分邊值的分數階微分包含多個正解的存在性問題 (1) 本文具體安排如下:在第1節中,我們給出了相關預備知識,包括問題描述、基本定義和相關引理,以及本文所需的條件假設;在第2節中,我們利用不動點定理給出了(1)存在多個正解的充分條件;在第3節中,舉出一個例子說明主要結果的有效性;在第4節中,對文章進行了總結。 這部分我們將介紹一些相關的基礎概念及定義,并介紹了一些對后續正解的存在性定理非常重要的引理。首先,我們將介紹一些關Caputo-Hadamard分數階微積分相關的內容, 定義1.1[14]連續函數x:[1,+∞]→R的α>0階的Hadamard分數階積分為 定義1.2[14]連續函數x:[1,+∞]→R的α>0階的Caputo-Hadamard分數導數為 (1)若對于任意的x∈X,F(X)是閉的(凸的),則稱多值映射F是閉的(凸的)。 (3)若對于X上所有的有界子集B,F(B)是相對緊的,則多值映射F是全連續的。 定義1.3[15](X,‖·‖)是一個賦范線性空間,多值映射Θ:X→p(X)。若對每一個x0∈X,集合Θ(x0)是X的一個非空閉子集,對于X中的每個包含Θ(x0)開子集B,存在x0的一個開鄰域V,使得Θ(V)?B,則稱Θ在X上是上半連續的。 定義1.4若對于每個x∈C([1,e],R),稱SF,x是F的選擇集合,定義為: SF,x={f∈L1([1,e],R):f∈F(t,x(t)),對于幾乎處處的t∈[1,e]} 定義1.5假設0<α≤1,λ≥0,d>0,x∈C([1,e]),滿足 并且存在f∈SF,x,使得x(t)滿足積分方程: 則x是以下邊值問題的唯一解 定義1.6[15]設X為Banach空間,C是X的閉凸子集,Pcp,c(C)表示C中所有非空緊凸子集集合。對于任意有界子集Ω?X,它的非緊測度為γ(Ω)=inf{d>0:Ω可以被有限多個直徑小于等于d的集合覆蓋} 定義1.7[15]多值映射F:[1,e]×R→P(R),若滿足: (1) 對于x∈[0,∞),t→F(t,x)是可測的,且對幾乎所有的t∈[1,e],x→F(t,x)是上半連續的,則F是Caratheodary的。 (2) 如果對每一個δ>0,存在φδ∈L1([1,e],R+),使得對幾乎所有的‖x‖≤δ和t∈[1,e],都有‖F(t,x)‖=sup{|w|:w∈F(t,x)}≤φδ(t),則F是L1-Caratheodary。 定義1.8[15]設X為Banach空間,若對于映射T:E?X→X,T連續且滿足條件:對每個有界子集Ω?E,均有γ(TΩ))≤k(Ω),則稱T為k-集壓縮映射(k≥0)。對于k<1的k-集壓縮映射稱為嚴格k-集壓縮映射。特別地,全連續映射是0-集壓縮映射,因此是嚴格k-集壓縮映射。 引理1.2[16]設X為Banach空間,令F是一個多值映射,滿足 F:[1,e]×R→Pcp,c(C)是L1-Caratheodary 令Θ:L1([1,e],R)→C([1,e],R)是一個連續線性算子,則 Θ。SF:C([1,e],R)→Pcp,c(C([1,e],R)),x→(Θ。SF)(x)=Θ(SF,x) 是C([1,e],R)×C([1,e],R)中的一個閉圖算子。其中C([1,e],R)表示[1,e]→R上的連續函數。 引理1.3[16]若Θ是上半連續當且僅當Θ存在一個閉圖象,即xn→x*,yn→y*,yn∈A(xn),有y*∈A(x*)。 (1)對?x∈?EΩr∩C,x?F(x); (2)對?h∈F(x),x∈?EΩL∩C,有‖h‖>‖x‖; (3)對?h∈F(x),x∈?EΩr∩C,有‖h‖≤‖x‖; (4)對?h∈F(x),x∈?EΩQ∩C,有‖h‖≥‖x‖。 其中,Ωr={x∈E:‖x‖ 為方便下文討論,給出下列記號: 設E=(C[1,e],‖·‖),范數定義為 顯然K是E上的一個錐。 定義算子 A:K→Pcp,c(C[1,e]), 下面給出本文假設條件如下: (H1)函數F:[1,e]×[0,∞]→Pcp,c([0,∞))是L1-Caratheodary,并且有非空的緊凸值。 (H2)存在一個不減函數φ:[0,∞]→(0,∞)和一個函數p∈L2([1,e]→R+),使得 ‖F(t,x)‖p:sup{|w|:w∈F(t,x)}≤p(t)φ(‖x‖) (H3)存在η∈C[1,e],η(t)>0,有 ‖F(t,x)‖q:inf{|w|:w∈F(t,x)}≥η(t)φ(‖x‖) (H4)存常數r>0,使得 (H5)存在ξ∈[1,e],0 (H6)存在ζ∈[1,e],0 為了得到微分包含邊值問題(1)的正解的存在性定理,先證明下面的引理: 引理1.5假設條件(H1)和(H2)成立,則算子A是一個上半連續的全連續算子。 證明第1步,A將E的有界集映射成為E中的有界集。 令Br={x∈E:‖x‖≤r}是K中的有界集。對于t∈[1,e],x∈Br時,f∈SF,x,令 則對t∈[1,e],由條件(H2)有 故當t∈[1,e]時有 從而A(Br)是一致有界的。 第2步,A是將有界集合映射到等度連續集。 令t1,t2∈[1,e]且t1 利用Lebesgue控制收斂定理知,當t1→t2時,有 因此,當t1→t2時,|h(t2)-h(t1)|→0,即A是等度連續的。由Ascoli-Arzelad定理,A是全連續的。 第3步,A存在一個閉圖,令xn→x*,hn→h*,hn∈A(xn),要證h*∈A(x*)。對于hn∈A(xn),則存在fn∈SF,xn,使得 定義線性算子: Θ:L1([1,e],[0,∞))→C([1,e],[0,∞)) 又因為hn(t)∈Θ(SF,xn),xn→x*,hn→h*。由引理1.2知,Θ是閉圖象算子,故h*∈Θ(SF,x*),即存在f*∈SF,x*,滿足 再由引理1.3知,A是上半連續的。 綜上,A是一個上半連續的全連續算子。 定理2.1若假設條件(H1)-(H6)都成立,則(1)至少存在兩個正解。 證明由引理1.5知A是一個上半連續的全連續算子,下面只需要證明A滿足引理1.4的所有條件,即可證明(1)至少存在兩個正解。 首先證明,A:K→Pcp,c(K),任給的x∈K,h∈A(x),那么存在w∈SF,x,有 又因為F:[1,e]×[0,∞)→Pcp,c([0,∞)),因此,當t∈[1,e]時 故有h∈K。即A:K→Pcp,c(K)。 下證,對?x∈?EΩr∩K,x?A(x)。用反證法,假設存在x∈?EΩr∩K,t∈[1,e],使得x∈A(x),‖x‖=r,存在w∈SF,x,利用H?lder不等式,有 故與假設(H4)矛盾。 其次證,對?h∈A(x),x∈?EΩL∩K,有‖h‖>‖x‖。任意x∈?EΩL∩K,則‖x‖=L。任意x∈K,存在w∈SF,x,當t∈[1,e],使得 由條件(H3)和(H5)可知 再證對?h∈A(x),x∈?EΩr∩K,有‖h‖≤‖x‖。任意x∈?EΩr∩C,則‖x‖=r。任意x∈K,存在w∈SF,x,t∈[1,e],使得 由條件(H2)和(H4)可知 由ξ∈[1,e]的任意性有‖h‖≤‖x‖。 最后證明,對?h∈A(x),x∈?EΩQ∩K,有‖h‖≥‖x‖。任意x∈?EΩQ∩K,則‖x‖=Q。任意x∈K,存在w∈SF,x,t∈[1,e],使得 由條件(H2)和(H6)知, 由ζ∈[1,e]的任意性有‖h‖≥‖x‖。 為了說明我們主要結果的有效性,下面給出一個簡單的例子。 (2) 其中α=0.7,λ=0,d=1。F:[1,e]×R→Pcp,c(R)的多值映射: 對于f∈F(t,x),有 因此, 計算知,當r>2.20時,滿足 若取r=2.21,存在ξ∈[1,e],當0 存在ζ∈[1,e],0 從而邊值問題(2)滿足引理2.1的所有條件,故根據定理2.1,(2)至少存在兩個正解。 本篇文章結合前人有關分數階微分方程正解的存在性研究,將單值推廣到多值,再利用多值映射的壓縮或拉伸不動點定理,研究了一類帶有積分邊值條件的Caputo-Hadamard型分數階微分包含正解的存在性問題,最后舉出一個簡單的例子說明結果的有效性。正解相比較一般的解更具有實際意義,而實際生活中問題復雜且受到多種因素的干擾,對于分數階微分包含模型的建立和正解的存在性研究造成很多困難,因此如何更有效的尋找到分數階微分包含的正解有待進一步的探究。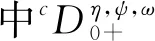
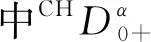

1 預備知識
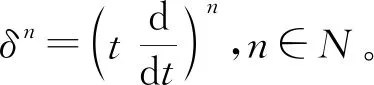


2 主要結果

3 例子
4 總結

