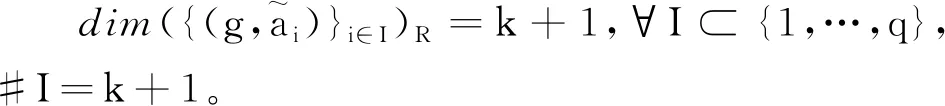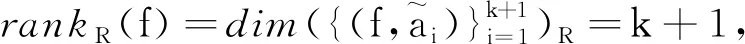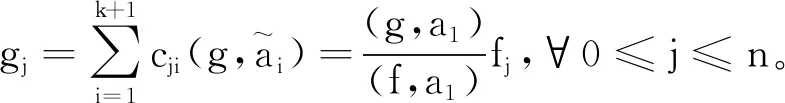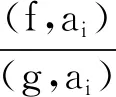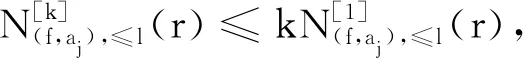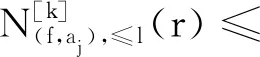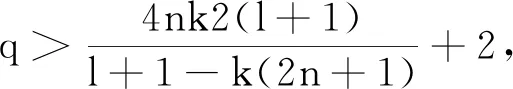亞純映射分擔(dān)移動(dòng)目標(biāo)的唯一性定理
曹廷彬,阮海洪
(1.南昌大學(xué)數(shù)學(xué)系,江西 南昌 330031;2.陸軍步兵學(xué)院,江西 南昌 330103)
最早研究亞純映射分擔(dān)移動(dòng)超平面的唯一性問(wèn)題要追溯到20年前的文[1-2],接著許多學(xué)者也研究這一方向,文章主要集中在文[3-19]。這些年來(lái),關(guān)于亞純映射分擔(dān)超平面和移動(dòng)超平面的唯一性問(wèn)題受到了許多學(xué)者的關(guān)注。關(guān)于這方面最讓人感興趣的研究方向有2個(gè):一個(gè)是超平面(移動(dòng)超平面)的最佳個(gè)數(shù)是多少?2009年,Chen-Yan[4]得到目前最佳超平面?zhèn)€數(shù)q=2n+3。2005年Thai-Quang[5]證明了在亞純映射為線性非退化的條件下移動(dòng)超平面的個(gè)數(shù)q=2n2+4n(n≥2)。而2007年,Chen-Li-Yan[6]在沒(méi)有要求亞純映射為線性非退化這一情形下,證明了移動(dòng)超平面的個(gè)數(shù)q=4n2+2n(n≥2)。2012年,Lü[7]改進(jìn)了Chen-Li-Yan[6]的結(jié)果得到q≥2n2+2n+3。隨后,Thoan-Quang-Duc[3]得到q>4n2+2即可。2013年,Quang-An[10]通過(guò)改進(jìn)Thai-Quang[19]關(guān)于移動(dòng)目標(biāo)的第二基本定理,并考慮q<4n2+2及截?cái)嘀財(cái)?shù)1的情形,獲得較文[3]更好的結(jié)果;另一個(gè)是考慮重值,重值的考慮是研究亞純映射分擔(dān)超平面(移動(dòng)超平面)唯一性問(wèn)題的一個(gè)重要課題,也有一些比較好的成果,比如Tu-Wang文[8],Cao-Liu-Cao文[9]等。本文主要在[10]中的兩個(gè)關(guān)于移動(dòng)目標(biāo)的第二基本定理的基礎(chǔ)上考慮重值得到帶截?cái)嘀財(cái)?shù)的第二基本定理,再利用這兩個(gè)第二基本定理討論了亞純映射分擔(dān)移動(dòng)目標(biāo)的唯一性問(wèn)題。
1 主要結(jié)果

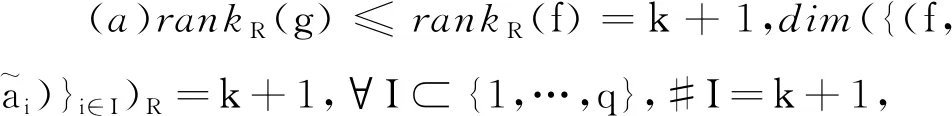
(b)dim{z∈Cm:(f,ai)(z)=(f,aj)(z)=0}≤m-2,1≤i (c){z∈Cm:0<ν(f,aj)(z)≤l}?{z∈Cm:0<ν(g,aj)(z)≤l},1≤j≤q。 (a)dim{z∈Cm:(f,ai)(z)=(f,aj)(z)=0}≤m-2,1≤i (b){z∈Cm:0<ν(f,aj)(z)≤l}?{z∈Cm:0<ν(g,aj)(z)≤l},1≤j≤q。 max{rankR(f),rankR(g)},有f=g。 1)令‖z‖=(|z1|2+…+|zn|2)1/2,z=(z1,…,zn)∈Cm,B(r):={z∈Cm:‖z‖ σ(z):=(ddc‖z‖2)m-1,η(z):=dclog‖z‖2∧(ddclog‖z‖2)m-1在Cm{0}上成立。 3)f:Cm→Pn(C)為一非常數(shù)亞純映射。(ω0,…,ωn}為Pn(C)上任意給定的齊次坐標(biāo),取Cm上全純函數(shù)f0,…,fn使得dimIf≤m-2,其中If:={z∈Cm:f0(z)=…=fn(z)=0},則稱 f=(f0:…:fn)為f的一個(gè)約化表示。 令a:Cm→Pn(C)為一亞純映射,且其約化表示a=(a0:…an),定義 4)對(duì)Cm上一個(gè)除子ν,k,D均為正整數(shù)或∞,定義ν的計(jì)數(shù)函數(shù): 對(duì)Cm上的一個(gè)亞純函數(shù)φ,我們記 為簡(jiǎn)便當(dāng)D=∞時(shí),我們可省略寫上標(biāo)D。 若對(duì)1≤j0<… 則當(dāng)r→∞,Ta(r)=o(Tf(r)),我們便稱a是(相對(duì)f)小映射。 2004年,Ru-Wang[20]引進(jìn)一個(gè)M上非退化的概念,如下: 定義2.1若dim(A)M=n+1,且對(duì)任意A中的非空真子集A1,(A1)M∩(AA1)M∩A≠φ,其中(A)M稱為域M上A的線性生成空間,則稱上述A在M上非退化。 若對(duì)任意A中的子集A1,#A1=n+1,有dim(A)M=n+1,則稱上述A處于一般位置。 為證明我們的結(jié)果,我們還需要以下定理,這些定理在Nevanlinna理論中充當(dāng)重要角色(見(jiàn)[10,21])。 定理2.1(關(guān)于移動(dòng)目標(biāo)的第一基本定理)f,a:Cm→Pn(C)為亞純映射且(f,a)≠0,則 Tf(r)+Ta(r)=mf,a(r)+N(f,a)(r) 注意到V(f)的定義與f的約化表示選取無(wú)關(guān),且易知rankR(f)=n+1-dimRV(f)。 又由定理2.1和定理2.2可得 令r→∞,有q≤k(k+2)。與已知q≥2k2+2k+3矛盾,因此V(f)?V(g)。從而有 rankR(f)=n+1-dimRV(f)≤n+1-dimRV(g)=rankR(g) 又已知rankR(g)≤rankR(f),于是rankR(g)=rankR(f),從而V(f)=V(g)。 ‖qTf(r)≤ 注意到l>k(k+2)-1,則 再結(jié)合定理2.2及上述不等式可得 整理得 ‖qTf(r)≤ ‖qTf(r)≤ 證明結(jié)合定理2.3,證明思路與引理3.2類似。 其中ks=q。對(duì)任意1≤i≤q,令 且 Pi=(f,ai)(g,aσ(i))-(g,ai)(f,aσ(i)) (3.1) 又由引理3.1,有V(f)=V(g)。 對(duì)給定的i(1≤i≤q),由(3.1),以及條件(c),(d)可知對(duì)υ∈{i,σ(i)},集合{z∈Cm:0<ν(f,aυ)(z)≤l}(?{z∈Cm:0<ν(g,aυ)(z)≤l})的每個(gè)元z0都是Pi的零點(diǎn),即 (3.2) 又?j∈{1,…,q}{i,σ(i)},則(f,aj)的任意零點(diǎn)z0是Pi的零點(diǎn)(除去一個(gè)余維≥2的解析集)。由上述討論,可得 (3.3) 另一方面,由Jensen公式,有 (3.4) 由不等式(3.3),(3.4),得 對(duì)上述不等式在i=1,…,q上求和,并由定理2.2和引理3.2,可得 整理得 o(T(r)) 定理1.2的證明假設(shè)f?g。記Tf(r)+Tg(r)=T(r)。由定理1.1的證明過(guò)程類似可得 整理得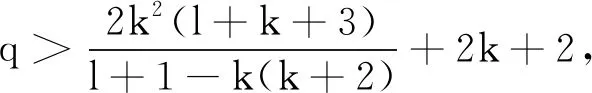
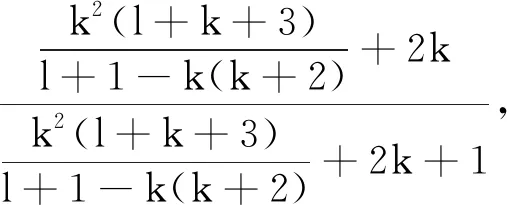
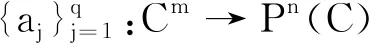
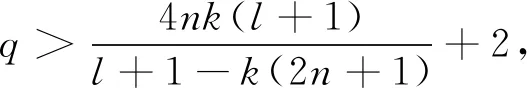

2 Nevanlinna理論中的基本概念和輔助結(jié)果




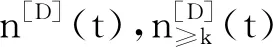
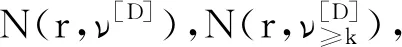

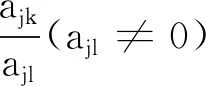

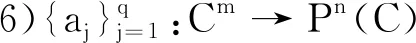


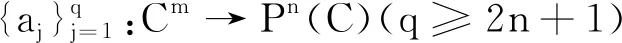
3 引理及定理證明
3.1 引理


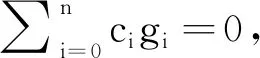


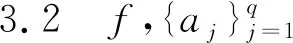
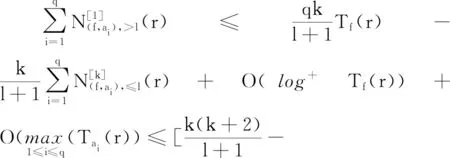

3.2 定理1.1、1.2證明