數形結合思想在小學數學教學中的應用

李志香

“數缺形時少直觀，形少數時難入微，數形結合百般好，割裂分家萬事休。”華羅庚先生用這首小詩向我們清晰地描述了數與形在解決數學問題中的關系，在教育界有深遠影響。在現今小學數學教材中，數形結合這一詞匯雖然沒有比較確切的定義，但在諸多概念和解題過程中都滲透著這一思想。

一、數形結合思想在“數與代數”中的應用

“數與代數”模塊是學生認識數量關系、探索教學規律以及建立數學模型的基石。它是小學生獲取基本數學知識、掌握數學基本思想的重要領域。因此，在此領域中數形結合思想應用頗多，研究素材也比較廣泛，筆者選取了小學計算教學中的一個難點問題加以闡述。

案例一：筆算乘法（人教版小學《數學》三年級下冊第四單元）——每套書有14本，王老師買了12套。一共買了多少本？

為了讓學生更輕松地達成本節課的教學要求，避免生硬灌輸，提高學生的動手操作能力，教師可以利用數形結合的方法幫助學生理解算理。首先，在學生自主探究14×12環節時，可以適時向學生引出點子圖作為研究的素材，以放手讓學生借助具體的實物進行大膽嘗試和探索，在探究計算方法的同時將數與形結合起來，從而激活學生的思維。

在合作交流環節，請學生上臺展示并且交流探索過程，可以讓學生明確劃分點子圖的不同方法，以及如何用算式將點子圖中的“形”進行正確的表征，從而建立起圖形表征和計算方法之間的聯系，進而使學生理解點子圖不同，計算方式也不盡相同，但都是采用了“先分后和”的思路，這恰恰也是計算兩位數乘兩位數的基本思路。

在總結提升環節，教師要引導學生將自行操作的點子圖抽象成矩形圖，對比分析點子圖和筆算乘法的步驟，這樣做就是讓學生借助圖形去掌握筆算兩位數乘兩位數的計算順序，理解隱藏其中的算理。讓學生將數學中的“數”與點子圖中的“形”結合起來，通過以形助數的方式，幫助學生理解兩位數乘兩位數的算理，讓學生在運算的過程中做到眼中有“數”，腦中有“形”。

二、數形結合思想在“圖形與幾何”中的應用

數形結合思想在圖形與幾何中的應用甚是廣泛，學好這部分內容不僅可以發展學生的空間觀念，還能使學生的思維得到質的飛躍。數形結合思想在這部分教學內容的應用主要體現為數形互化，即用數正確表示圖形，用形正確表示數。

案例二：認識面積（人教版小學《數學》三年級下冊第五單元）——下面兩個圖形，哪個面積大？

在“認識面積”這堂課中，為了讓學生理解“幾何中的面即面積中的‘形，面的大小即為‘數”的道理，在教學中筆者利用數形結合思想主要設計了以下環節：

① 創設情境，激發度量的需要。在日常生活中，我們經常要度量面的大小，如粉刷一面墻，這面墻有多大；灑水車給植物澆水，這片植物的種植面積有多大等，這都需要準確刻畫它們的面積。通過創設豐富的現實情境，引發學生的思考，從而激發學生的學習動機。

② 親歷度量過程，體會面積大小。單位化思想是度量的核心，學習長度時，學生已有了度量的經驗。因此，在此課例教學中，教師可以引導學生用學過的圖形作單位，度量長方形的面積。度量長方形面積時，教師可以給學生提供三種學具：圓形、三角形、正方形。讓學生通過擺一擺的方式，親歷探索過程，從而認識到：圓形不能密鋪，不能用幾個圓形來代表長方形的面積；三角形和正方形都可以密鋪——進而在數單位圖形個數的過程中，體會面積的含義與大小。

③ 借助多媒體，展示數形統一。教學中利用PPT中的動畫功能直接展示面積單位的形成過程，從而讓學生深刻理解為什么要用正方形作面積單位、基本面積單位都有哪些以及面積單位在生活中的應用。通過設計豐富的活動，使學生認識面積之形；在度量的過程中實現以數解形，使學生經歷面積的形成過程；在體驗中完善和豐富對面積單位的認識和度量。

三、數形結合思想在“綜合與實踐”中的應用

在小學數學學習中，“綜合與實踐”部分內容比較耗時、耗力，學生也不太容易掌握。如果教師能夠結合學生的生活經驗去滲透數形結合思想，不僅可以改變學生數學學習方式，還可以幫助學生全面認識、了解數學。

案例三：“植樹問題”（人教版小學《數學》五年級上冊第七單元）——同學們在全長100 m的小路一邊植樹，每隔5 m栽一棵（兩端要栽）。一共要栽多少棵樹？

在小學數學中，植樹問題一般是指按照一定的路線和不同的植樹要求，讓學生通過獨立探索，留心發現間隔數和植樹的棵數之間的關系，從而解決問題的一類題型。在這類學習活動中，植樹的路線是不固定的，簡單的植樹路線就是一條封閉路線，復雜點的植樹問題路線則是一條線段。對于小學生而言，一條線段的植樹問題比較困難，因為情況比較復雜。它可以分為以下情形：兩端都栽、只有一端栽、兩端都不栽。為了讓學生更好地掌握本節課的知識，教師可以利用數形結合思想教會學生用畫線段圖的方式分析問題、解決問題：

① 兩端都栽：栽樹棵樹=間隔數+1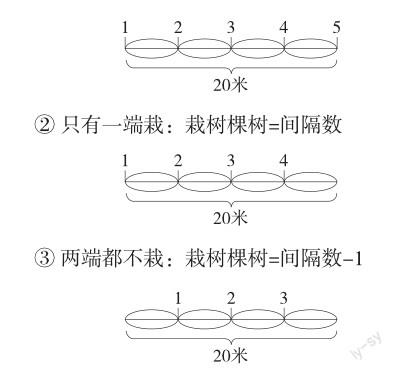

同樣，教師也可以利用數形結合的方法，采用畫線段的方式幫助學生分析封閉型的植樹問題，讓學生通過畫線段圖的方式，直觀地看出環形植樹：栽樹棵樹=間隔數。在教學植樹問題時，數形結合思想主要體現在教會學生利用畫線段圖的方式理清數量間的邏輯關系，從而發現栽樹棵樹和間隔數之間的關系，最終達到解決問題的目的。

（作者單位：江蘇省淮安市洪澤第二實驗小學）

責任編輯：王 燕