基于涌水影響半徑的隧道涌水量預測方法研究

張修杰 周學民 韋未 張偉鋒

摘要：

受斷裂構造和降水等因素的共同影響，火成巖地區形成了一定規模的富水斷層破碎段。當隧道穿越這類巖層時，極易發生涌水災害而造成人員傷亡和設備損失。針對上述涌水問題，根據火成巖區富水斷層破碎段的特點，將隧道涌水量分為基巖裂隙水釋放量和降水入滲量兩個主要組成部分，通過地下水疏干法預測基巖裂隙水釋放量，同時利用降水入滲法預測降水入滲量。在此基礎上，為提高涌水預測精度，引入了實測涌水量數據擬合的動態涌水影響半徑參與計算，并推導出基于涌水影響半徑的涌水量預測方法，最后以鴻圖隧道后續開挖段為例對該方法進行驗證。研究結果表明：① 在一個降雨周期內，含水層平均厚度Hn越大，對應的影響半徑Rn具有更高的增長速率；② 隨著涌水時間T增加，影響半徑Rn的增長率逐漸降低；③ 所提方法的隧道涌水量計算結果與實際監測數據的誤差在10%以內，可靠性較高。研究成果可為類似地質條件下的地下工程建設提供理論指導。

關 鍵 詞：

深埋特長隧道； 涌水量預測； 涌水動態影響半徑； 斷裂構造

中圖法分類號： U452.1+1

文獻標志碼： A

DOI：10.16232/j.cnki.1001-4179.2023.05.023

0 引 言

隧道在施工過程中會出現一些復雜的施工條件，特別是深埋越嶺隧道的穿越建設，破壞了原有圍巖的結構，因而施工期常遇見涌水、突水（突泥）等災害，易造成一系列的惡劣后果［1-2］，對人員財產安全構成重大威脅［3-4］。

國內外許多學者都對隧道的涌水進行分析預測：El Tani［5］修正了亥姆霍茲方程，用于研究半無限含水層下圓形隧道的涌水；Joo 等［6］采用層流和紊流的理論方法，研究了孔隙水壓力與涌水量的關系；Moon等［7］考慮了地下水位下降與涌水量的關系，提出了新的估算分析方法；胡力繩等［8］探究了地下水、圍巖、注漿圈和襯砌共同形成的水壓平衡體系中4個因素之間的共同作用；朱成偉等［9］利用保角變換推導了雙線平行隧道和上下分布的雙洞隧道的地下滲流場；Zhao等［10］通過模型試驗和數值模擬分析了地表水存在對隧道襯砌注漿厚度和涌水量的影響；Tan等［11］研究了襯砌的不均勻性與其他水力因素之間的相互作用，用于預測襯砌外水壓狀況，進而分析出襯砌后隧道涌水量。

對比于其他巖體，擁有較高飽和抗壓強度和飽和抗剪斷強度的安山玢巖、凝灰巖等火成巖因其堅硬、穩定，通常被認為是理想的地下工程修建區域。修建在火成巖區的隧道、隧洞等地下工程設施一般情況下只在通過構造帶、斷層富水破碎帶、軟弱巖層段的時候出現冒頂坍塌、特大突水等安全風險［12-13］。但由于地質勘察和施工設備的局限性、巖體裂隙普遍存在和隨機生成的特性，使得難以在施工現場準確識別和確定地下水流入隧道的所有有效因素，部分涌水預測方法存在較大的誤差［4，14］，給隧道開挖階段涌水預測帶來一定的挑戰［15］。

本文以鴻圖深埋隧道為研究對象，依據施工前期水文地質勘察對富水斷裂帶的勘測成果以及開挖期的涌水監測數據，分析一個降雨周期內的涌水特征，探究隧道開挖涌水引起隧址區域地下水位劇烈下降后的地下水降落漏斗影響半徑變化規律，并基于曲線擬合手段構建適用于隧道工程穿越斷裂帶的涌水量計算模型。

1 隧道涌水的傳統經驗預測

1.1 工程概況

鴻圖特長隧道設計全長約6 300 m，最大埋深約為751 m，隧址區地層主要為侏羅系高基坪組火山巖，出露巖石主要為燕山期巖漿巖，形成多期侵入接觸帶。隧道修建過程中跨越了斷層構造發育帶，其中東西走向和近南北走向次級斷裂和節理發育，巖體破碎。

隧址區水資源豐沛，區內水系分屬韓江水系和榕江水系，多年平均降雨量1 865.6 mm，蒸發少，因此巖層富水性較好。水文地質勘察結果顯示：隧址區地下水主要為降水補充，地下水類型分為松散巖類孔隙水和基巖裂隙水，地下水補給途徑通暢，補給來源充沛。隧道施工過程中也產生了大量的高壓涌水，威脅施工安全。

1.2 傳統經驗預測方法

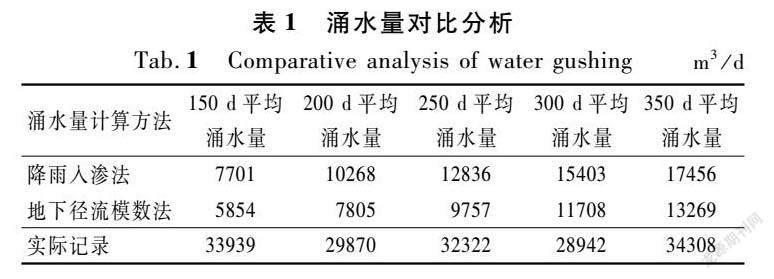
針對隧址區的工程地質和水文地質條件，在施工前期嘗試使用傳統的降雨入滲法和地下徑流模數法來計算不同時間段的單日平均涌水量，為應對隧道施工中涌水量提供參考性意見。但施工現場情況表明，這兩種方法與實際涌水量存在較大誤差（詳見表1）。傳統的降雨入滲法和地下徑流模數法的計算原理與簡易水均衡法一致，本質上屬于水均衡法的另一種形式。涌入隧道內的地下水，除來源于大氣降水和地表水系之外，還來自于山體的基巖裂隙水。雖然山體的基巖裂隙水同樣來源于大氣降水和地表水系，但山體的基巖裂隙水是在漫長的地質構造運動中，由大量降水和地表水沿斷層破碎帶深入巖體內部形成的穩定的地下水體。山體的基巖裂隙水與涌入隧道內的、來源于大氣降水和地表水系的地下水存在時空積蓄的差異。傳統的降雨入滲法和地下徑流模數法在涌水預測過程中沒有將這種時空積蓄的差異納入考慮范疇，也就忽略了基巖裂隙水對隧道涌水量的影響。

當隧道埋深較淺（<50 m）時，基巖裂隙水受限于山體內含水層的規模而儲量較小，可忽略不計，傳統方法預測隧道涌水量將較為準確；但當隧道埋深較大（＞100 m）時，龐大的山體在地質構造運動中足以形成一定規模儲量的基巖裂隙水，此時傳統方法預測隧道涌水量的準確性將受限于基巖裂隙水的儲量。

此外，傳統方法在預測隧道涌水量時，均采用固定的匯水面積。匯水面積的估算受水文地質勘察工作的精度影響，而且長期施工過程中，在隧道的涌水影響半徑下，地下流場產生復雜的變化，進而使匯水面積也相繼發生不同程度的變化，大大影響涌水預測的準確度。

另一方面，在對埋深大（特）長隧道進行涌水預測的過程中，對全隧道段同時進行單日涌水量預測，作為全隧道段單日涌水量的傳統方法已不可行。在對埋深大（特）長隧道進行單日涌水量預測時，應該考慮富水斷層破碎帶區域的分布和施工進度的共同影響，將已開挖段和巖層受擾動隧道段進行分段涌水量預測。隧道分段時，應根據隧道內不同圍巖的含水介質特征、圍巖性質與級別、推測通過斷裂破碎帶情況和斷裂破碎帶寬度及其趨勢特征、施工進度等因素劃分。為了提高隧道涌水量預測的準確性，針對研究區域特征，引入涌水影響半徑概念，結合水文地質勘察結果，以現場實測涌水記錄為依據，進行涌水量預測研究。

2 涌水影響半徑規律

2.1 基本設定

隧址區含水層規模大，含水層中裂隙網絡發育，滲透性良好，基巖裂隙水儲量巨大。在隧道開挖涌水后，將引起隧址區域地下水位的劇烈下降，涌水影響半徑隨之增大，地下水的匯水面積也不斷擴大，龐大的山脈以及發育的斷層構造保證了巖體深部地下水補給的穩定。當獲得新的補給量與隧道涌水量之間已經達到新的動態平衡時，就會形成新的動態穩定流場，隧道涌水量將維持一個相對動態穩定的狀態。

隧址區儲存的大量基巖裂隙水具有豐富的降雨補充、低蒸發與地下水多級分水嶺的特點，遵循水均衡法的基本原理，對研究區域作如下假定。

（1） 隧道上方巖體的給水度一定時間內不發生變化，地下水持續、及時地沿斷層構造補充到隧道上方巖體中。

（2） 隧址區巖體含水層之間的水力聯系一定時間內不發生變化，只與固有的地質構造有關，但在地下水長時間流動情況下，構造裂隙仍會發生變化。

（3） 隧址區地下水水頭在一定時間內不發生驟變，處于基本穩定狀態。

（4） 擬建隧道高程以下水系、基巖裂隙水不直接對隧道涌水造成影響。

（5） 構造裂隙使鄰近巖體之間保持穩定的水力聯系同時也產生相互的影響，涌水影響半徑在鄰近巖體之間呈有梯度的緩慢變化。

2.2 涌水量與影響半徑基本關系

隧道的涌水量計算過程中，需要將目標隧道段分段開展研究。假定隧道研究區段涌水總量Q等于隧道各段涌水量Qn的總和。Qn由基巖裂隙水釋放量Wn（1）和降雨入滲的補給量Wn（2）兩大部分組成。基巖裂隙水釋放量Wn（1）采用地下水疏干法計算，降雨入滲補給量Wn（2）采用動態影響半徑的降雨入滲法計算，預測帶中的含水層厚度為平均含水層厚度，其計算公式如下：

2.3 計算參數選取

在2.2節中已經明確了隧道涌水量與影響半徑等參數的關系式，本節將說明計算過程所需參數的選定情況。

（1） 計算分段劃分。根據隧道內不同圍巖的含水介質特征、圍巖性質與級別、推測通過斷裂破碎帶情況和斷裂破碎帶寬度及其趨勢特征、施工進度等因素劃分計算段。把入口至K91+285段已開挖隧道段和巖層受擾動隧道段沿線分為N個預測計算段，各段長度Ln為10～110 m。隨著隧道的不斷掘進，N會不斷增大，最終N個分段的總長度將等同于隧道實際開挖長度。研究時間從隧道內的第1次涌水開始，設置5個研究節點，研究節點分布如下：① T=150 d，N=23；② T=200 d，N=24；③ T=250 d，N=25；④ T=300 d，N=26；⑤ T=350 d，N=27。

（2） 計算參數確定。根據工程地質和水文地質勘察資料，各區段具體選取參數如圖1所示。各分段參數選取說明如下：① 各火山巖富水裂隙段和富水斷層破碎段含水層平均厚度為11～587 m；② 研究段巖體給水度為0.001～0.025；③ 表層風化巖層降水入滲系數為0.2～0.3；④ 隧址區多年平均降雨量為1 865.6 mm。

3 現場涌水驗證

為驗證式（13）涌水影響半徑的擬合精確度，選擇該隧道后續施工段K91+700～K91+950進行驗證，通過對比涌水量計算值與實際監測值進行評估。該安山巖段總長250 m，共施工掘進42 d；受張性斷層F2-5的影響，該段巖體破碎，在地下水持續補充作用下，形成了富水斷層破碎帶。根據巖體給水度差異，以0.000 5 的差異梯度為劃分標準，將250 m長的富水斷層破碎帶劃分為接續的6段，記錄施工過程中各段揭露富水裂隙區域和富水斷層破碎區域產生涌水的時間，忽略鄰近隧道段滲水量影響，具體參數詳見表3。

將表3的參數代入式（10）中，得到該施工段影響半徑隨涌水時間的變化值，截至42 d時計算得涌水影響半徑最大為808 m。

將各時間點下涌水影響半徑的計算結果代入式（13）中得出K91+700～K91+950段涌水量計算值。為驗證計算結果的正確性，將涌水的實際監測值與涌水計算值進行對比，如圖4所示。

由圖4可以看出：在42 d內涌水計算值曲線的變化趨勢與實際監測值曲線的變化趨勢基本一致，兩者均隨涌水時間增加而不斷減少；在涌水的1～6 d內涌水計算值略大于實際監測值，平均誤差為7%；7～42 d涌水實測結果存在一定的波動情況，但整體上與計算值結果較為接近，整體最大誤差不超過5%。

兩曲線存在誤差的原因如下：① 當巖體裂隙網絡發達、圍巖給水度較大時，分段圍巖之間存在一定的連通性，開挖擾動區域裂隙后，使得周邊富水斷裂帶中的基巖裂隙水沿巖體裂隙網絡涌入到隧道內，導致實測結果存在一定的波動情況。② 實測值是點監測，而數學模型屬數理統計，本身存在系統誤差，但總體上模型計算與實際監測值相近。

4 結 論

（1） 在涌水量預測計算中，匯水面積應采用動態面積，動態變化因素為涌水影響半徑。在一個降雨周期內，含水層平均厚度Hn對影響半徑Rn的影響逐漸顯著，Hn越大，對應的Rn將具有更高的增長速率；隨著涌水時間T增加，影響半徑Rn的增長率逐漸降低，涌水影響半徑總體呈非線性增加。

（2） 定義的6 d處拐點和170 d處拐點，把隧道涌水時間段較為準確地分為3段，分別為特大涌水量時間段、較大涌水量時間段及緩增涌水量時間段。

（3） 在埋深大且受富水斷層裂隙聯動影響下，為提高一個降雨周期內的涌水影響半徑計算精度，施工中應及時判斷富水斷裂帶規模，以提高涌水預測評估的準確性。

（4） 對存在于火成巖富水斷層裂隙區域內的破碎巖體，施工過程中及時加固并進行錨固支護，減少隧道基巖裸露長度，對于減少隧道內涌水量尤為重要。

參考文獻：

［1］ 劉志春，王夢恕.隧道工程因素對地下水環境影響研究［J］.巖土力學，2015，36（增2）：281－288.

［2］ 張頂立，孫振宇，宋浩然，等.海底隧道突水演化機制與過程控制方法［J］.巖石力學與工程學報，2020，39（4）：649-667.

［3］ NIKVAR H A，KATIBEH H，FARHADIAN H.Numerical analysis of steady-state groundwater inflow into Tabriz line 2 metro tunnel，northwestern Iran，with special consideration of model dimensions［J］.Bulletin of Engineering Geology and the Environment，2016，75：1617-1627.

［4］ FARHADIAN H，KATIBEH H.New empirical model to evaluate groundwater flow into circular tunnel using multiple regression analysis［J］.International Journal of Mining Science and Technology，2017，27（3）：415-421.

［5］ EL TANI M.Helmholtz evolution of a semi-infinite aquifer drained by a circular tunnel［J］.Tunnelling and Underground Space Technology，2010，25：54-62.

［6］ JOO E J，SHIN J H.Relationship between water pressure and inflow rate in underwater tunnels and buried pipes［J］.Géotechnique，2014，64（3）：226.

［7］ MOON J，FERNANDEZ G.Effect of excavation-induced groundwater level drawdown on tunnel inflow in a jointed rock mass［J］.Engineering Geology，2010，110（3）：33－42.

［8］ 胡力繩，王建秀，盧耀如.考慮地下水、注漿及襯砌影響的深埋隧洞彈塑性解［J］.巖土力學，2012，33（3）：757-766.

［9］ 朱成偉，應宏偉，龔曉南，等.水下雙線平行隧道滲流場解析研究［J］.巖土工程學報，2019，41（2）：355-360.

［10］ ZHAO X，YANG X.Experimental study on water inflow characteristics of tunnel in the fault fracture zone［J］.Arabian Journal of Geosciences，2019，12（13）：399-411.

［11］ TAN Y Q，SMITH J V，LI C Q，et al.Predicting external water pressure and cracking of a tunnel lining by measuring water inflow rate［J］.Tunnelling and Underground Space Technology，2018，71：115－125.

［12］ 蔡俊華.穿越花崗巖蝕變帶的隧道突涌機理及施工許可評價方法研究［D］.武漢：中國地質大學（武漢），2018.

［13］ 胡義新，陳培帥.小凈距隧道富水破碎帶突水災變演化規律與防治技術［J］.公路，2016，61（7）：325-329.

［14］ 謝偉，楊緒波.基于解析法對折多山隧道進行分段涌水量預測計算［J］.公路，2019，64（4）：318-32.

［15］ 程小勇，黃勤健.深埋隧道斷裂帶涌水量預測分析［J］.人民長江，2021，52（8）：133-136，150.

（編輯：劉 媛）

Abstract：

Under combined influences of fracture tectonics and precipitation，a certain scale water-rich faults have been formed in the igneous region.When tunnels pass through such regions，it is highly possible to cause water gushing and loss of life and equipment.For the above water gushing problems，according to the analysis of the water-rich fault fracture section characteristics in the igneous area，the tunnel water gushing was considered to be composed of two major components：those released from bedrock fractures and those from precipitation infiltration.The former was predicted by the groundwater desiccation method，while the latter was predicted by the precipitation infiltration method.On this basis，in order to gain a higher accuracy of the prediction results，the influence radius fitted by the measured data was involved in the calculation，and a method for water gushing prediction was deduced based on the influence radius.Finally，an example of Hongtu Tunnel was illustrated for verification.The results showed that：① within a rainfall cycle，the larger average thickness of the aquifer（Hn）there was，the higher growth rate of the corresponding influence radius（Rn）would be.② With the increase of the time T，the growth rate of the radius of influence Rn was gradually reduced.③ The error of the calculation results of the proposed method and the actual monitoring data was within 10%，and the accuracy was high.The research results can provide theoretical guidance for the construction of underground projects under similar geological conditions.

Key words：

deep-buried long tunnel；prediction of water gushing；dynamic influence radius of water gushing；fracture structure