基于有限元的邊坡穩定可靠度改進一次二階矩法研究

汪安南，林潮寧，李同春，2，齊慧君，邵天成

(1.河海大學水利水電學院，江蘇 南京 210024；2.水安全與水科學協同創新中心，江蘇 南京 210024)

1 研究背景

邊坡失穩引起的滑坡災害已成為全球范圍內主要地質災害之一[1]。由大型邊坡失穩和滑坡引起的工程事故歷史上屢見不鮮[2]，且其造成的后果也是不可估計的，因此邊坡的抗滑穩定安全度研究成為國內外工程界十分關心的研究課題[3]。目前，在邊坡穩定性分析方面的研究大致可以分為2類：一類是由極限平衡法和數值計算方法所組成的確定性分析方法[4]；另一類是考慮參數隨機性、變異性的可靠性分析方法[5]。相比于確定性分析，可靠性分析方法考慮了參數不確定性對邊坡穩定性的影響，更接近實際情況。

常用的邊坡可靠性分析方法主要有蒙特卡洛法、響應面法及一次二階矩法等。李育超等[6]將蒙特卡洛法與有限元法相結合，利用隨機走步法不斷更新試算滑動面，確定了邊坡臨界滑動面及其對應的最小安全系數；何淑軍等[7]采用蒙特卡洛法對夏呀河四級滑坡進行可靠性分析，定量地表達了該滑坡的安全程度；周罕等[8]采用響應面法和強度折減法相結合的分析方法，把安全系數和破壞概率作為綜合評價邊坡穩定性的指標，從不同角度對邊坡可靠性進行分析；陳昌富等[9]基于響應面法建立了一種高效的邊坡可靠指標和失效概率近似計算方法，大大降低了構造響應面函數的計算工作量；朱彥鵬等[10]基于改進一次二階矩法建立了錨定板擋土墻的系統可靠度分析模型，分析了參數在不同變異系數下對系統可靠度指標的影響和土性參數敏感性。通常，當功能函數為隱式時，僅蒙特卡洛法和響應面法可用，但蒙特卡洛法的模擬次數多，計算效率低；響應面法通過不同的響應面函數重構隱式功能函數，但采用傳統響應面形式處理復雜問題計算精度有限，采用機器學習算法構建響應面函數涉及超參數選取等問題，計算復雜度高[11]。

考慮上述方法在處理邊坡隱式極限狀態函數時的問題，本文提出一種基于有限元的邊坡穩定可靠度改進一次二階矩法，定義極限狀態函數為滑體極限狀態下抗滑力與下滑力的差值，考慮黏聚力及內摩擦角作為隨機變量并且服從獨立正態分布，求出極限狀態方程中隨機變量的偏導數，基于改進一次二階矩法編寫了求解邊坡失穩概率和可靠指標的計算程序，通過算例驗證了所提方法的適用性，并對某庫岸邊坡進行了可靠性分析。

2 顯式極限狀態函數的建立及改進一次二階矩法原理

2.1 邊坡顯式極限狀態函數

有限元迭代解法[3]是一種以剛體極限平衡基本思想為基礎的直接迭代解法，是一種在滑動面已知情況下邊坡穩定分析的有效方法，不僅可計算出邊坡沿已知滑動面的安全系數，且能同時給出邊坡臨界失穩時的位移場與應力場。

用有限元迭代解法分析時，邊坡穩定的非線性特性主要反映在滑動面上，滑動面上的強度準則一般采用摩爾-庫倫準則。滑動面的單元形式主要采用文獻[12]中提出的常規的矩形(平面)或立方體(空間)的統一模式。當邊坡處于臨界穩定狀態時，滑動面上的滑動力和阻滑力滿足

(1)

式中，m為危巖體內滑動面單元個數；Wi為第i個滑動面單元上的法向力；Pi為第i個滑動面單元上的切向力；Ai為第i個滑動面單元上扣除受拉區后的面積；ci為第i個滑動面單元上的黏聚力；φi為第i個滑動面單元上的內摩擦角；K為假定安全系數；K*為真實的抗滑穩定安全系數。

由于力的矢量特征，安全系數為在邊坡潛在滑動面上總抗滑力矢在整體下滑趨勢方向上投影的代數和與總下滑力矢在此方向上投影代數和的比值。當滑體處于極限平衡狀態時，安全系數即為極限抗滑力與下滑力的代數和比值。將邊坡滑動面上的滑動力達到抗滑力作為邊坡極限狀態的標志，故將抗力函數R和作用函數S相等的情況作為極限狀態，即

(2)

式中，S(g)為作用函數；R(g)為抗力函數；g為函數變量；Z0為功能函數。對隨機變量求偏導數得

(3)

式中，Z為功能函數；fi為第i個滑動面單元上的內摩擦系數；X為隨機變量的向量表示，X1i、X2i分別為X的第1個、第2個隨機變量。

2.2 改進一次二階矩法的基本原理及計算步驟

(4)

(5)

根據隨機變量線性組合的性質及可靠指標的定義，可得

(6)

對式(3)、(4)進行變換，得設計驗算點在原始X空間中的坐標為

xi=μXi+βσXicosθXi

(7)

3 算例驗證

3.1 計算模型

含有1個確定性滑面的邊坡算例是邊坡穩定分析中非常經典的例子[13]，其二維模型結構清晰，受力狀態簡單，可以得到其力學上的解析解。單一接觸面巖質滑坡體幾何尺寸見圖1。巖土體抗剪強度參數視為隨機變量，服從正態分布，具體數值見表1。

圖1 單一接觸面巖質滑坡體截面(單位：m)

表1 巖土體物理力學參數

相關研究顯示，變量之間的相關性對可靠指標的影響較小，可以認為是相互獨立的[14-15]，暫不考慮黏聚力與內摩擦角的相關性。目前研究中[16-17]，對于巖土體黏聚力及內摩擦角變異系數的取值均在0.1～0.3范圍內，本算例巖質材料的黏聚力及內摩擦角的變異系數取值為0.15。邊坡顯式極限狀態函數中滑動面上各單元的切向力及法向力采用非線性有限元方法求取，綜合考慮時間和計算精度，建立有限元計算模型，見圖2。共560個單元，609個節點。底部基巖的兩側和底部邊界均為固定約束，上部滑動塊體為自由邊界。

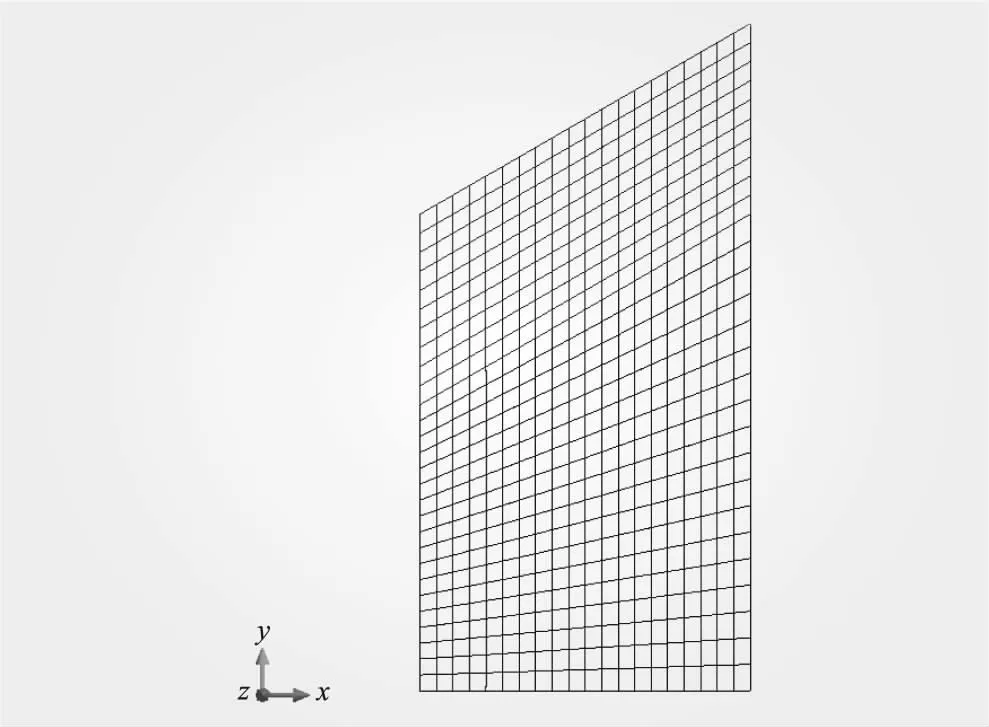
圖2 有限元計算模型

3.2 計算過程與分析

荷載考慮邊坡自身重力，采用非線性有限元計算滑動面上單元切向力、法向力，建立邊坡滑動面的顯式極限狀態函數；依據驗算點法的邊坡可靠性分析流程，進行可靠指標的迭代計算。按照本文的邊坡可靠指標計算流程，共進行2輪可靠指標的迭代計算即滿足精度要求，所以該邊坡的可靠指標為1.493 9，其破壞概率為6.76%。

通常，蒙特卡洛法計算結果可作為基準解[18]。為驗證本文所提方法計算結果的準確性，結合蒙特卡洛法與有限元強度折減法，經過100 000次的蒙特卡洛模擬，得到該邊坡的失效概率為6.18%，計算耗時約為6.0×105s(166.67 h)，總抗滑力投影與下滑力投影差值分布見圖3。從圖3可知，本文方法計算結果與蒙特卡洛法計算結果相比，誤差在3%以內，說明本文方法計算出來的失效概率與蒙特卡洛法的計算結果具有可比性，計算結果合理可行。

圖3 邊坡總抗滑力投影與下滑力投影差值分布

同時，采用其他目前常用的可靠性分析方法對該邊坡算例進行計算，結果見表2。基于本文建立的顯式極限狀態函數，采用均值一次二階矩法對該邊坡算例進行可靠性分析，失效概率為12.04%，此結果與蒙特卡洛法計算結果相比，誤差為94.82%。采用基于二次多項式響應面函數的改進一次二階矩法對該邊坡算例進行可靠性分析，失效概率為5.21%，此結果與蒙特卡洛法計算結果相比，誤差為15.70%。說明本文所提方法相比于均值一次二階矩法、響應面法具有更高的計算精度。此外，相比于響應面法的較高計算復雜度，本文方法計算過程簡單易于操作，能考慮滑坡體、巖基力學特性的不均勻性及滑動面上的應力分布影響。

表2 可靠性計算結果

4 工程應用

4.1 工程概況

某庫岸邊坡位于右岸壩前，距大壩900～1 700 m，坡高650～700 m，為花崗巖巖質邊坡，陡傾岸內及岸外構造發育。根據地質勘探結果，該庫岸巖體分為散體結構、碎裂結構、塊裂結構和鑲嵌一次塊狀結構4種。其中，散體結構水平厚度一般小于30 m，碎裂結構一般在40～60 m，塊裂結構一般在50～80 m。此外，岸坡平臺還分布幾條拉裂陷落帶，其中規模較大的有LF54和LF55等。3號梁庫岸巖體結構見圖4。

圖4 庫岸巖體結構

4.2 計算模型

本文選取3號梁地質剖面，底部全長1.582 km，高差0.788 km。在此基礎上，建立了1組整體穩定分析模型和3組局部穩定性分析模型，見圖5、6。為考慮該變形體是否存在整體失穩的可能，對庫岸沿變形和非變形界限的抗滑穩定性進行分析，選取了3號梁地質剖面，以地質勘查推測的變形范圍界限和碎裂巖體下限為假定滑動面。對于局部穩定分析，指定滑動面以頂部平臺出露的LF54為后緣拉開面，以巖體結構面為假定滑面，以不同埋深深度分別進行分析，局部計算模型見圖6。

圖5 整體穩定計算模型

圖6 局部穩定計算模型

由于本文給出的極限狀態函數含有邊坡滑動面各單元的切向力及法向力，采用非線性有限元法計算，根據工程地質剖面圖，建立相應的數值模型，見圖7。綜合考慮計算時間和精度，有限元計算模型共1 616個單元，1 736個節點；邊界條件為下部固定，左右兩側水平約束，上部為自由邊界。

圖7 穩定性分析模型

覆蓋層除外，計算模型巖體參數取值見表3。考慮滑動面抗剪強度參數指標c、f為隨機變量進行可靠度分析，結合同類巖土工程經驗，可以認為各滑動面強度參數服從正態分布，統計特性指標見表4。由于邊坡上建筑物荷載條件未明確，故未考慮坡體加載的影響。

表3 巖體力學參數取值

表4 結構面參數統計特征值

4.3 計算過程與分析

采用非線性有限元法計算滑動面單元的切向力和法向力，建立滑動面的顯式極限狀態函數；依據驗算點法的邊坡可靠度分析流程，對整體及局部共4種假定滑動面進行可靠指標的迭代計算，直到滿足精度為止；為對邊坡的安全狀態有更全面的認識，采用巖體及各滑動面強度參數的平均值作為標準值，采用有限元強度折減法進行安全系數計算，計算結果見表5。

從表5可知，整體及局部的安全系數均高于現行邊坡規范抗滑穩定安全系數控制下限值1.15，然而局部的失穩概率較高，需適當的采取工程措施以降低風險。該計算結果與實際監測中邊坡局部出現拉裂、位錯及坡面坍塌等變形破壞但整體保持穩定的現象互相印證。安全系數與可靠性分析對邊坡局部狀態判斷出現矛盾的原因是：①表征邊坡穩定性的安全系數沒有考慮材料參數的變異性，低估了邊坡局部的失穩風險；②散體結構帶和碎裂結構帶淺表部材料參數雖然均值較高，但是變異性大(滑動面巖土體的變異系數都達到0.3)，導致邊坡局部失穩概率較大。

表5 各計算模型可靠指標計算結果

因此，應采取分級放坡[8]，加強對邊坡的支護處理。為保持邊坡的長久穩定，應植草對坡面進行防沖刷處理，對外露的坡面采用格構式等形式進行護坡。在做好坡上截水、坡體排水、坡面防護等綜合治理的同時，應加強對邊坡的監測及數據分析，做好災害的主動防范，提前預報。

5 結 語

針對蒙特卡洛法與響應面法在處理邊坡隱式極限狀態函數時的問題，本文提出了一種基于有限元的邊坡穩定可靠度改進一次二階矩法，建立了邊坡顯式極限狀態函數，并應用于某庫岸邊坡可靠性分析中，得出以下結論：

(1)與已有的可靠性分析不同，本文定義極限狀態函數為滑體極限狀態下抗滑力與下滑力的差值，考慮黏聚力及內摩擦角作為隨機變量并且服從獨立正態分布，求出極限狀態方程中隨機變量的偏導數，在降低計算復雜度，提升計算效率的同時保證計算精度，計算精度上優于響應面法，計算效率上優于蒙特卡洛法。

(2)采用本文提出的邊坡可靠度分析方法，多角度綜合分析了某庫岸邊坡的穩定性。由于滑坡穩定性分析不可能考慮全部的影響因素，因此除了巖土體的抗剪強度參數黏聚力、內摩擦角外，考慮其他參數影響的邊坡可靠性分析需要進一步研究。