基于隨機響應面法的結構可靠度敏感性分析理論及其工程應用

季 昀，段 杭，孟亞運，王 霄，李同春

(1.國家能源局大壩安全監察中心，浙江 杭州 310014；2.中國電建集團華東勘測設計研究院有限公司，浙江 杭州 310014；3.中國三峽建工(集團)有限公司白鶴灘工程建設部，四川 成都 610041；4.中國電建集團中南勘測設計研究院有限公司，湖南 長沙 410014；5.淮安市水利勘測設計研究院有限公司，江蘇 淮安 223001；6.河海大學水利水電學院，江蘇 南京 210024)

0 引 言

結構可靠度敏感性分析，或稱為結構可靠度靈敏度分析，是結構可靠度分析的重要組成部分。通過結構可靠度敏感性分析，可以得到各輸入隨機變量分布參數的變化引起失效概率變化的不同程度，從而確定各參數對結構安全影響的重要程度，為工程設計、施工和管理供有益的指導與反饋。

依據結構可靠度敏感性分析的定義，不難得到一次二階矩法等結構可靠度算法所對應的敏感性分析公式。然而，由于一次二階矩等方法僅適用于功能函數為顯式的情況，而重力壩等復雜結構的可靠度分析功能函數通常為隱式函數，此時，基于一次二階矩法的結構可靠度敏感性分析公式將不再適用。作為一種新興的代理模型方法(Metamodel，Model of model)，隨機響應面法采用隨機多項式[1](一般為Hermite正交多項式)作為響應面函數，相比于經典響應面法所采用的序列多項式，具有明確的數學意義和理論證明的收斂特性[2]。近年來，隨機響應面法及基于隨機響應面法的非侵入式隨機有限元法在工程結構可靠度分析中得到了一定的推廣和應用[3-7]。然而，目前尚未出現有關結構可靠度隨機響應面法敏感性分析及其應用方面的文獻。Sudret[8]采用隨機多項式進行了系統敏感性分析，但其研究的對象是物理系統，且對應的敏感性分析研究本質上屬于方差分析的范疇，與結構可靠度敏感性分析的定義并不相同。Isukapalli[9]在其博士論文中研究了“Coupling of the SRSM with sensitivity analysis methods”，并編寫了相關計算程序SRSM-ADIFOR。但是，Isukapalli的研究僅僅是得到了隨機響應面方程對于各隨機變量的偏導公式，而結構可靠度敏感性分析真正需要求解的應是失效概率對于各隨機變量及其特征參數的偏導公式。

一般地，由于隨機響應面法的基本變量均為標準正態隨機變量，故可以將隨機響應面法與幾何法結合起來求解結構可靠指標和失效概率。本文將推導幾何法與隨機響應面法相結合的結構可靠度敏感性分析公式，并應用于工程實例。

1 基于一次二階矩方法的結構可靠度敏感性分析

一次二階矩法在均值點將功能函數進行展開，在應用時具有諸多的局限性[10]。但是，作為最早出現的結構可靠度計算方法，該方法概念清晰，便于闡述結構可靠度敏感性分析的概念。因此，在介紹基于隨機響應面法的結構可靠度敏感性分析理論前，首先給出基于一次二階矩方法的結構可靠度敏感性分析計算公式及其推導過程。

一般情況下，可以認為失效概率與可靠指標具有如下一一對應的關系

Pf=1-Φ(β)

(1)

式中，Pf為失效概率；Φ(·)為標準正態分布的累積概率分布函數；β為可靠指標。

由式(1)，可得

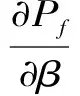
(2)

式中，φ(·)為標準正態分布的概率密度函數；其他各變量含義同前。

當輸入基本隨機變量向量x相互獨立且功能函數為線性時，有

(3)

(4)

式中，μxi為輸入隨機變量xi的均值；ai為線性功能函數g的表達式中xi所對應的系數；σg為功能函數g的標準差。則失效概率Pf對于均值μxi和標準差σxi的敏感性可表示為

(5)

(6)

當基本隨機變量向量x中各變量相互獨立且功能函數為非線性時，可得失效概率Pf對于均值μxi和標準差σxi的敏感性為

(7)

(8)

2 基于隨機響應面法的結構可靠度敏感性分析

隨機響應面法是一種全局響應面法，因而基于該方法的敏感性分析是具有實際物理意義的，而以經典響應面法(序列多項式響應面法)為代表的局部響應面法通常并不具有這樣的特性。此外隨機響應面法的基本變量均為標準正態隨機變量，可以方便地將隨機響應面法與幾何法結合起來求解結構可靠指標和失效概率。

對任意設計變量b(可以代表任一隨機變量的均值或標準差)，結構的失效概率對其敏感性可表述為

(9)

式中，b為任意設計變量；其余各符號含義同前。

當在結構可靠度隨機響應面法中采用幾何法計算結構的可靠指標時，可靠指標的求解可等效表述為幾何法中的約束問題。當分析結構失效概率對設計變量b的敏感性時，有

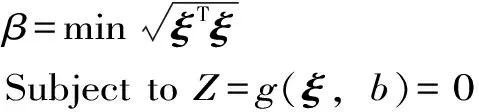
(10)

式中，ξ為結構的輸入隨機變量向量為輸入變量向量x經一定的變量轉換運算得到一組新的標準正態隨機空間內的隨機變量向量，且ξ=(x-μx)/σx={ξ1，ξ2，…，ξn}T；其他各符號含義同前。

δβ=?ξL(ξ)δξ

(11)

式中，δβ為可靠指標β相對于變量b的變分；δξ為輸入隨機變量向量ξ相對于變量b的變分；L(ξ)=(ξTξ)1/2；?ξL(ξ)表示L(ξ)對于正態分布的隨機向量ξ的矢量導數。

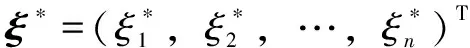
δg=?bgδb+?ξgδξ=0

(12)

式中，?bg為極限狀態方程g在點ξ*和b0處對不同取值的變量b構成的向量b的矢量導數；?ξg為極限狀態方程g在點ξ*和b0處對輸入隨機向量ξ的矢量導數。

根據非線性規劃的相關理論，上式須在b*處滿足Kuhn-Tucker條件，而這可以通過引入拉格朗日乘子λ來實現。于是，式(10)所示的約束問題最終轉化為

?ξL(ξ)+λ?ξg(ξ)=0

Subject toZ=g(ξ*，b0)=0

(13)

由式(12)，易得

?bgδb=-?ξgδξ

(14)

將式(14)代入式(13)，可得

?ξLδξ=λ?bgδb

(15)

綜上，可靠指標對于任意變量b的敏感性可表示為

(16)

式(16)中的拉格朗日乘子λ可以由Kuhn-Tucker條件?ξL(ξ)+λ?ξg(ξ)=0求得。對該方程兩邊同取歐式范數(2-范數)，有

(17)

由于拉格朗日乘子λ為負實數，因此有

(18)

當上述推導過程中的變量b表示為任一輸入隨機變量ξi(i=1，2，…，n)的均值時，有

(19)

(20)

故可靠指標β對于輸入隨機變量向量的均值的敏感性計算公式可表示為

(21)

同理，若將變量b表示為任一輸入隨機變量ξi(i=1，2，…，n)的標準差時，類似可得

(22)

式(21)、式(22)與式(3)、式(4)在形式上是一致的，這表明，式(3)、式(4)為式(21)、式(22)的一種特殊形式。類似地，可得采用幾何法的結構可靠度隨機響應面中失效概率Pf對于均值μxi和標準差σxi的敏感性計算公式為

(23)

(24)

顯然，式(23)與式(24)結果均為無量綱的數值，可以用于衡量失效概率對于不同輸入隨機變量的敏感性。如用隨機響應面函數替代式(23)和式(24)中的極限狀態方程g，即得到幾何法與隨機響應法相結合的結構可靠度算法的敏感性分析公式。

3 算例驗證及工程應用

3.1 算例——非線性方程

(25)

式中，ξ1、ξ2均為標準正態隨機變量，分別由結構輸入隨機變量x1、x2轉化而來。

令ξ={ξ1，ξ2}，x={x1，x2}，則有

(26)

式中，μx為輸入隨機變量向量x的均值向量，且μx={1 000，250}；μx為輸入隨機向量x的標準差向量，且σx={200，37.5}。

可以認為，隨機響應面法擬合得到的功能函數即為結構實際的功能函數。則求得結構功能函數分別對各基本變量ξi(i=1，2)的偏導表達式如下

(27)

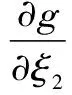
(28)

采用幾何法求得標準正態空間內的設計驗算點為ξ={ξ1，ξ2}={0.625 6，-2.244 9}，將其代入式(27)和式(28)，分別得到在設計驗算點附近結構功能函數對各基本隨機變量ξi(i=1，2)的偏導數分別為-3.103和6.596 3。

于是，不難得到結構功能函數對輸入隨機變量的2-范數為

(29)

根據前述推導得到的采用幾何法的結構可靠度隨機響應面敏感性分析公式，求得結構失效概率對各輸入隨機變量的均值敏感度如式(30)和式(31)所示，對標準差的敏感度如式(32)和式(33)所示。

(30)

(31)

(32)

(33)

由式(30)和式(31)可見，在設計驗算點附近，結構失效概率將隨著輸入隨機變量x1均值的增加而增大，隨著輸入隨機變量x2均值的增加而減小；當隨機變量x1和x2的標準差增加(或稱隨機變量的變異系數增加)時，結構的失效概率都會增加。

由文獻[11]中對輸入隨機變量x1和x2的描述可知，x1為懸臂梁所受荷載，x2為懸臂梁的截面尺寸。由此可以認為，該懸臂梁的結構失效概率將隨著荷載均值的增加而增大，隨著截面尺寸均值的增加而減小，符合工程經驗認識。同時，荷載與截面尺寸的標準差的增大(或稱變異系數的增大)將導致結構失效概率的增大，也即結構可靠指標減小。

3.2 工程應用——重力壩

某水電站位于柬埔寨的Kamchay河干流，擋水建筑物為混凝土重力壩，最大壩高112 m，壩頂寬6.0 m，壩體上游面84m高程以上為豎直面以下坡度為1∶0.3；下游面折坡點高程為145.00 m，折坡點以下坡度為1∶0.75。

選取最大壩高斷面(5號壩段)進行分析，該壩段建基面高程為41 m，壩頂高程為153 m，壩底寬97 m，上游正常蓄水位150 m。建立該壩段的二維有限元分析網格模型，壩基在上下游方向各延伸200 m，壩基深度取為200 m，有限元網格模型如圖1所示。根據壩體混凝土所采用的型號，壩體彈性模量取值范圍為21.5～25.5 GPa；試驗得到的壩基巖體彈性模量取值范圍為3～8 GPa。利用實測位移監測數據對其進行反演分析后，得到該壩段的壩體彈性模量均值為21.88 GPa，壩基彈性模量均值為4.64 GPa。參考類似工程，假定壩體彈模Ec、壩基彈模Er及大壩上游水位Hu3個隨機變量的變異系數分別取為0.15、0.20、0.06，如表1所示。

圖1 重力壩有限元網格模型

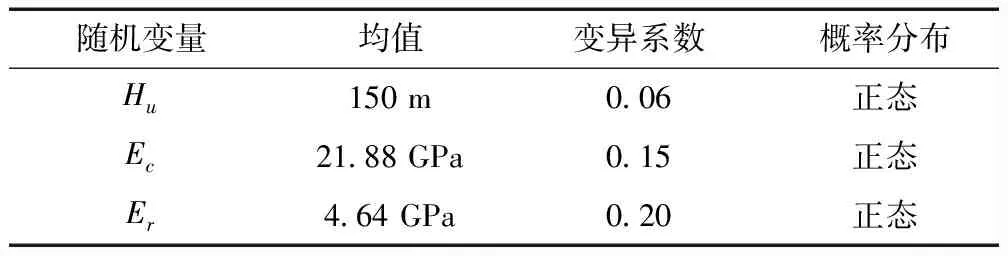
表1 各隨機變量統計特性

采用非侵入式隨機有限元法(隨機響應面法+有限元法)進行結構可靠度分析時的計算流程如圖2所示。

圖2 基于非侵入式隨機有限元法的結構可靠度隨機響應面法計算流程

根據圖2所示的計算流程，首先，建立本實例的重力壩壩踵抗拉可靠度功能函數為

Z=g(x)=g(Hu，Ec，Er)=6.79-wt

(34)

式中，x為輸入隨機變量向量；wt為重力壩壩踵的拉應力區寬度，m。

與式(34)意義類似，如果壩踵的拉應力區是連續的，可以以壩基面上距離壩踵6.79 m處的垂直向應力σy的正負來形成重力壩的抗拉功能函數

Z=g(x)=-σy

(35)

式中，σy為壩基面上距離壩踵7/100壩底寬度處的垂直向應力，應力符號以拉為正，以壓為負。

顯然，由于引入了有限元分析，得wt到關于輸入隨機變量向量x的顯式表達式是比較困難的，因此，式(34)與式(35)所示的功能函數均為隱式方程。

將輸入的非標準正態分布隨機變量向量x=(x1，x2，x3)轉換為服從N(0，12)的標準正態隨機向量ξ=(ξ1，ξ2，ξ3)，其中，x1代表大壩上游水位Hu；x2代表壩體彈性模量Ec；x3代表壩基彈性模量Er。

應用自編結構可靠度隨機響應面法程序，得到重力壩抗拉可靠度的二階隨機響應面函數如式(36)所示。經驗算，二階隨機響應面函數和三階隨機響應面函數精度相差較小，故選擇二階隨機響應面函數用于重力壩結構抗拉可靠度計算是合適的。

(36)

以式(36)作為重力壩結構抗拉可靠度的功能函數，應用幾何法求得重力壩抗拉可靠指標為1.629，對應的失效概率為5.17%。標準正態空間的設計驗算點為[-0.765，-0.387，-1.385]，將其轉換至原始變量空間為[143.115 m，20.609 GPa，3.355 GPa]。

求得結構功能函數分別對各基本變量ξi(i=1，2，3)的偏導

(37)

(38)

(39)

采用幾何法，得到標準正態空間內的設計驗算點為ξ=(-0.765，-0.387，-1.385)，將其代入式(37)～式(39)，得到在設計驗算點附近結構功能函數分別對各基本變量ξi(i-1，2，3)的偏導數依次為89.573 1、45.247 0和161.992 3。

于是，不難得到結構功能函數對輸入變量向量偏導的2-范數為

(40)

根據前述推導得到的采用幾何法的結構可靠度隨機響應面敏感性分析公式，求得結構失效概率對各輸入隨機變量的均值敏感度如式(41)～式(43)所示，對標準差的敏感度如式(44)～式(46)所示。

(41)

(42)

(43)

(44)

(45)

(46)

分析式(41)～(43)可知，在設計驗算點處，該重力壩的結構抗拉失效概率對于各輸入隨機變量均值的敏感性排序為：壩基彈性模量Er>壩體彈性模量Ec>大壩上游水位Hu。同時，結構抗拉失效概率對于各輸入隨機變量均值的敏感度均為負值，這說明在設計驗算點處，壩基彈性模量越大、壩體彈性模量越大或大壩上游水位越高(設計驗算點處的上游水位為143.115 m，低于正常蓄水位150 m)都將降低結構的抗拉失效概率。

分析式(44)～(46)可知，在設計驗算點處，該重力壩的結構抗拉功能函數對于各輸入隨機變量標準差的敏感性排序為：壩基彈性模量Er>大壩上游水位Hu>壩體彈性模量Ec。同時，結構抗拉失效概率對于各輸入隨機變量標準差的敏感度均為正值，這說明在設計驗算點處，壩基彈性模量變異越大、壩體彈性模量變異越大或大壩上游水位波動越大都將增加結構的抗拉失效概率。

綜上所述，壩基彈性模量的均值與標準差對其抗拉可靠度最為敏感。因此，建議通過補強灌漿等方式提高壩基的彈性模量，可以顯著提高該重力壩結構抗拉可靠指標。

4 結 論

本文推導了幾何法與隨機響應面法相結合的結構可靠度敏感性分析公式，并應用于工程實例，得到了相關結論。研究表明：

(1)本文給出的基于隨機響應面法和幾何法的結構可靠度敏感性分析公式可有效分析和比較失效概率和可靠指標對于各隨機變量的敏感程度。

(2)將本文給出的計算公式應用于懸臂梁和某重力壩結構可靠度分析的實例，收到了良好的效果，得到了有益的結論。對于該重力壩，壩基彈性模量的均值與標準差對其抗拉可靠度最為敏感。因此，本文建議通過補強灌漿等方式提高壩基的彈性模量，可顯著提高其壩踵抗拉可靠指標。