模型大不確定下的導(dǎo)彈姿態(tài)控制系統(tǒng)設(shè)計

周 航，張文杰，周建平，夏群利

(1.北京理工大學(xué)宇航學(xué)院， 北京 100081； 2.北京電子工程總體研究所， 北京 100854)

1 引言

隨著導(dǎo)彈武器技術(shù)的不斷發(fā)展，現(xiàn)代化戰(zhàn)爭對導(dǎo)彈的機(jī)動性和快速性等要求大幅提高，尤其是在高超聲速再入、強(qiáng)機(jī)動突防和跨域變外形等復(fù)雜作戰(zhàn)場景下，控制系統(tǒng)的設(shè)計呈現(xiàn)出強(qiáng)耦合、強(qiáng)非線性、快時變和大不確定性等特點(diǎn)。傳統(tǒng)的控制系統(tǒng)設(shè)計方法難以滿足現(xiàn)代化戰(zhàn)爭以及未來智能化戰(zhàn)爭對導(dǎo)彈控制能力的要求，迫切需要進(jìn)行模型大不確定下的智能控制系統(tǒng)設(shè)計。

近年來，學(xué)術(shù)界對導(dǎo)彈這類復(fù)雜非線性系統(tǒng)控制方法進(jìn)行了廣泛的研究[1-4]，其中動態(tài)逆[5-7]設(shè)計方法能夠增強(qiáng)非線性條件下控制系統(tǒng)的性能，從而得到了一定應(yīng)用。但是基于動態(tài)逆的設(shè)計方法通常對飛行器模型建模精度要求較高，在復(fù)雜戰(zhàn)場環(huán)境和自身強(qiáng)耦合特性下，模型大不確定導(dǎo)致其難以實(shí)現(xiàn)有效控制。滑模控制(sliding mode control，SMC)由于原理及結(jié)構(gòu)簡單，對外界干擾具有較強(qiáng)的魯棒性，且能夠根據(jù)不同的控制要求設(shè)計各種形式的滑模面，例如快速終端滑模[8]、非奇異滑模[9]等，目前已被廣泛應(yīng)用于工程控制領(lǐng)域。但是滑模控制系統(tǒng)的設(shè)計也很大程度上依賴于被控對象模型的準(zhǔn)確性，因此當(dāng)模型不確定時，需要結(jié)合其他方法實(shí)現(xiàn)對模型不確定部分的預(yù)測。神經(jīng)網(wǎng)絡(luò)算法源于對人腦功能特征的模仿，網(wǎng)絡(luò)具有高度非線性，同時具備自主化、自進(jìn)化的學(xué)習(xí)能力，非常適合處理大不確定性和模糊性的問題。神經(jīng)網(wǎng)絡(luò)中的徑向基函數(shù)(radial basis function，簡稱RBF)神經(jīng)網(wǎng)絡(luò)具有萬能逼近特性，收斂速度較快，同時具備較好的泛化能力[10]。因此，可將RBF神經(jīng)網(wǎng)絡(luò)與滑模控制相結(jié)合，實(shí)現(xiàn)導(dǎo)彈模型大不確定下的智能自適應(yīng)控制。在RBF神經(jīng)網(wǎng)絡(luò)與滑模控制相結(jié)合方面，已有部分學(xué)者對其開展了相關(guān)研究[11-18]，研究主要側(cè)重于RBF神經(jīng)網(wǎng)絡(luò)對系統(tǒng)所受外界擾動的估計，通過對擾動的補(bǔ)償提高控制系統(tǒng)的魯棒性，但是較少考慮系統(tǒng)自身模型大不確定對控制系統(tǒng)設(shè)計帶來的問題。

導(dǎo)彈系統(tǒng)模型的不確定性主要來自于跨空域、寬速域和外界干擾條件下動力學(xué)系數(shù)的不確定性以及操縱機(jī)構(gòu)的控制不確定性，例如舵面受損、摩擦阻滯效應(yīng)等。本文基于RBF神經(jīng)網(wǎng)絡(luò)提出了一種導(dǎo)彈智能自適應(yīng)姿態(tài)控制系統(tǒng)設(shè)計方法，首先結(jié)合滑模理論建立姿態(tài)控制系統(tǒng)動力學(xué)方程，然后僅根據(jù)系統(tǒng)的輸入輸出信息，運(yùn)用RBF神經(jīng)網(wǎng)絡(luò)智能感知系統(tǒng)的動力學(xué)特性，進(jìn)而逼近系統(tǒng)中的不確定項(xiàng)，通過對控制律及網(wǎng)絡(luò)權(quán)值更新律的設(shè)計，實(shí)現(xiàn)模型大不確定情況下的導(dǎo)彈姿態(tài)智能自適應(yīng)控制。最后通過數(shù)學(xué)仿真驗(yàn)證該控制系統(tǒng)設(shè)計方法的有效性，對于提升導(dǎo)彈的飛行穩(wěn)定性和控制魯棒性具有一定的現(xiàn)實(shí)意義。

2 姿態(tài)控制系統(tǒng)建模

對于側(cè)滑轉(zhuǎn)彎(skid-to-turn，STT)控制的導(dǎo)彈，姿態(tài)控制的核心在于對滾轉(zhuǎn)通道進(jìn)行穩(wěn)定，從而避免因彈體滾轉(zhuǎn)帶來的氣動耦合效應(yīng)；對于傾斜轉(zhuǎn)彎(bank-to-turn，BTT)控制的導(dǎo)彈，姿態(tài)控制需要根據(jù)過載指令分配原則，快速準(zhǔn)確地調(diào)整彈體傾斜角以保證縱側(cè)向的精確制導(dǎo)。因此無論是何種控制方式，對滾轉(zhuǎn)通道的姿態(tài)控制都是實(shí)現(xiàn)導(dǎo)彈精準(zhǔn)打擊的關(guān)鍵。本節(jié)主要建立滾轉(zhuǎn)通道的導(dǎo)彈動力學(xué)模型以及基于滑模控制理論的姿態(tài)控制系統(tǒng)模型。

2.1 動力學(xué)系統(tǒng)建模

導(dǎo)彈在高速大機(jī)動運(yùn)動狀態(tài)下滾轉(zhuǎn)通道與偏航通道耦合嚴(yán)重，為了實(shí)現(xiàn)滾轉(zhuǎn)通道的姿態(tài)控制，建立如式(1)所示的動力學(xué)系統(tǒng)模型：

(1)

式(1)中：γ為導(dǎo)彈滾轉(zhuǎn)角；ωx為彈體滾轉(zhuǎn)角速度；q為大氣動壓；Sref為導(dǎo)彈的特征面積；Lref為導(dǎo)彈的特征長度；Jx為繞彈體軸的轉(zhuǎn)動慣量；mx為滾轉(zhuǎn)力矩系數(shù)，包括了橫側(cè)向的耦合力矩系數(shù)，可進(jìn)一步表示為

(2)

2.2 滑模控制系統(tǒng)建模

根據(jù)導(dǎo)彈滾轉(zhuǎn)通道動力學(xué)模型，取彈體滾轉(zhuǎn)角及角速度為控制系統(tǒng)的狀態(tài)量，即

x=[x1x2]T=[γωx]T

(3)

將式(2)和式(3)代入式(1)中，建立彈體姿態(tài)控制系統(tǒng)模型：

(4)

式(4)中：cωx、cδx、cβ、cωy、cδy為滾轉(zhuǎn)通道對應(yīng)的動力學(xué)系數(shù)，計算表達(dá)式如下：

取滾轉(zhuǎn)舵偏角為系統(tǒng)控制量，即u=δx；令f(x)=-cωxx2，g(x)=-cδx；將氣動耦合項(xiàng)視為控制系統(tǒng)的時變干擾項(xiàng)，即d(t)=-cββ-cωyωy-cδyδy，且滿足|d(t)|≤D(D≥0且有界)，則式(4)可寫為

(5)

令姿態(tài)角指令為x1d，則系統(tǒng)的響應(yīng)誤差為e=x1d-x1，對控制誤差求導(dǎo)得：

(6)

由此可設(shè)置滑模函數(shù)為

(7)

其中，k>0。

對式(7)求導(dǎo)并結(jié)合式(5)和式(6)可得：

(8)

假設(shè)控制系統(tǒng)模型完全已知，即f(x)和g(x)可測，設(shè)計控制律：

(9)

將式(9)代入式(8)可得：

(10)

取η≥D，由Lyapunov到達(dá)條件可得：

(11)

然而導(dǎo)彈在復(fù)雜大動態(tài)環(huán)境下存在氣動參數(shù)攝動，導(dǎo)致模型中的f(x)和g(x)實(shí)際無法準(zhǔn)確獲得；另外，導(dǎo)彈操縱機(jī)構(gòu)可能存在性能下降或者在大擾動下摩擦阻滯效應(yīng)嚴(yán)重。故接下來采用RBF神經(jīng)網(wǎng)絡(luò)自適應(yīng)感知系統(tǒng)模型的不確定項(xiàng)，從而得到相應(yīng)項(xiàng)的估計值，解決滑模控制律的設(shè)計問題，最終完成導(dǎo)彈姿態(tài)的智能自適應(yīng)控制。

3 模型不確定下的智能自適應(yīng)控制

從姿態(tài)控制系統(tǒng)模型可以看出，系統(tǒng)模型的不確定性主要來自動力學(xué)參數(shù)的不確定以及舵控效應(yīng)的不確定。其中，氣動耦合項(xiàng)參數(shù)不確定可通過滑模控制對干擾項(xiàng)具有魯棒性進(jìn)行解決，即通過設(shè)置合理的切換增益來消除耦合小量的影響；而對于控制系統(tǒng)主要動力學(xué)參數(shù)和舵控效應(yīng)不確定的問題，可結(jié)合神經(jīng)網(wǎng)絡(luò)的強(qiáng)大感知能力來進(jìn)行自適應(yīng)估計補(bǔ)償。因此，本節(jié)分別對2種模型不確定情況進(jìn)行基于RBF神經(jīng)網(wǎng)絡(luò)的智能自適應(yīng)魯棒控制系統(tǒng)設(shè)計。

3.1 動力學(xué)模型不確定情況

當(dāng)動力學(xué)模型不確定時，采用RBF神經(jīng)網(wǎng)絡(luò)來逼近模型中的f(x)和g(x)，閉環(huán)控制系統(tǒng)結(jié)構(gòu)如圖1所示。

圖1 閉環(huán)控制系統(tǒng)結(jié)構(gòu)圖

圖1中的RBF神經(jīng)網(wǎng)絡(luò)是一種三層神經(jīng)網(wǎng)絡(luò)，包括輸入層、隱含層和輸出層，其輸入輸出算法為

(12)

其中：x為網(wǎng)絡(luò)輸入；j為網(wǎng)絡(luò)隱含層第j個節(jié)點(diǎn)；h=[hj]T為高斯基函數(shù)的輸出；cj為高斯基函數(shù)的中心；bj為高斯基函數(shù)的寬度參數(shù)；W*和V*為逼近f(x)和g(x)的理想網(wǎng)絡(luò)權(quán)值；εf和εg為網(wǎng)絡(luò)逼近誤差，且|εf|≤εMf，|εg|≤εMg。

(13)

設(shè)計自適應(yīng)滑模控制律為

(14)

其中，η≥D。

將f(x)和g(x)分別記為f和g，并將式(12)—式(14)代入式(8)可得：

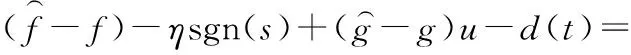
(15)

定義Lyapunov函數(shù)為

(16)

其中，γ1>0，γ2>0。

對式(16)求導(dǎo)得：

(17)

將式(15)代入式(17)中可得：

s(-εf-ηsgn(s)-εgu-d(t))

(18)

設(shè)計神經(jīng)網(wǎng)絡(luò)權(quán)值向量的自適應(yīng)更新律為

(19)

將式(19)代入式(18)中可得

(20)

3.2 舵控模型不確定情況

除動力學(xué)模型大不確定外，導(dǎo)彈在飛行過程中可能會遭遇來自敵方攔截武器的攻擊以及來自惡劣交變環(huán)境的影響，對控制系統(tǒng)最直接的影響體現(xiàn)在舵效的變化，例如舵面受損、舵機(jī)摩擦阻滯等。

考慮上述影響因素，可將控制系統(tǒng)描述為

(21)

式(21)中：δ(x)為舵效變化導(dǎo)致的舵片偏轉(zhuǎn)附加值，與系統(tǒng)狀態(tài)量和外界擾動有關(guān)，是大不確定項(xiàng)。

因此，如果導(dǎo)彈在運(yùn)動過程中出現(xiàn)了舵效變化的情況，根據(jù)原系統(tǒng)生成的名義控制量和實(shí)際控制量將存在不確定誤差，進(jìn)而導(dǎo)致控制系統(tǒng)性能變差。此時可結(jié)合RBF神經(jīng)網(wǎng)絡(luò)的逼近能力對δ(x)進(jìn)行預(yù)測估計，從而實(shí)現(xiàn)控制信號的補(bǔ)償。

RBF神經(jīng)網(wǎng)絡(luò)輸入輸出算法為

(22)

其中：Q*為逼近δ(x)的理想網(wǎng)絡(luò)權(quán)值；εδ為網(wǎng)絡(luò)逼近誤差，且|εδ|≤εMδ；其他參數(shù)同式中的定義。

取網(wǎng)絡(luò)輸入為x=[x1x2]T，RBF神經(jīng)網(wǎng)絡(luò)輸出為

(23)

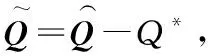
(24)

此時，根據(jù)式(21)求得滑模函數(shù)的導(dǎo)數(shù)為

(25)

設(shè)計舵控模型不確定下的智能補(bǔ)償控制律為

(26)

將式(26)和式(24)代入式(25)中可得：

(27)

定義Lyapunov函數(shù)為

(28)

其中，γ>0。

結(jié)合式(27)對式(28)求導(dǎo)得：

(29)

設(shè)計神經(jīng)網(wǎng)絡(luò)權(quán)值向量的自適應(yīng)更新律為

(30)

取η≥|gεδ+D|，并將式(30)代入式(29)，可得：

(31)

由式(31)可知，所設(shè)計的控制方法具有穩(wěn)定性。

4 仿真分析

采用所設(shè)計的模型大不確定下的智能自適應(yīng)控制方法進(jìn)行數(shù)學(xué)仿真，驗(yàn)證其對導(dǎo)彈姿態(tài)的控制性能。針對動力學(xué)模型不確定情況，選取動力學(xué)參數(shù)cωx=0.1，cδx=7；設(shè)計控制系統(tǒng)參數(shù)為：γ1=500，γ2=6，k=10，η=60；干擾項(xiàng)設(shè)為d(t)=50。RBF神經(jīng)網(wǎng)絡(luò)的高斯基函數(shù)參數(shù)取為ci=[-2 -1 0 1 2]，bi=5。令姿態(tài)角指令為γd=sin(t)，為防止指令在零附近發(fā)生劇烈抖振，仿真中采用飽和函數(shù)代替符號函數(shù)，得到仿真結(jié)果如圖2—圖6所示。

由仿真結(jié)果可知，控制系統(tǒng)的姿態(tài)角γ與姿態(tài)角速度ωx響應(yīng)良好，姿態(tài)角速度的變化在0.5 s內(nèi)收斂。采用所設(shè)計的RBF神經(jīng)網(wǎng)絡(luò)預(yù)測方法得到了較為準(zhǔn)確的系統(tǒng)不確定項(xiàng)f(x)和g(x)的估計值，達(dá)到了對系統(tǒng)不確定性估計的目的。由于系統(tǒng)的不確定性，控制指令u在初始時刻存在抖振，但能夠在0.5 s內(nèi)收斂，驗(yàn)證了所設(shè)計的控制系統(tǒng)的有效性。

圖2 姿態(tài)角指令跟蹤曲線

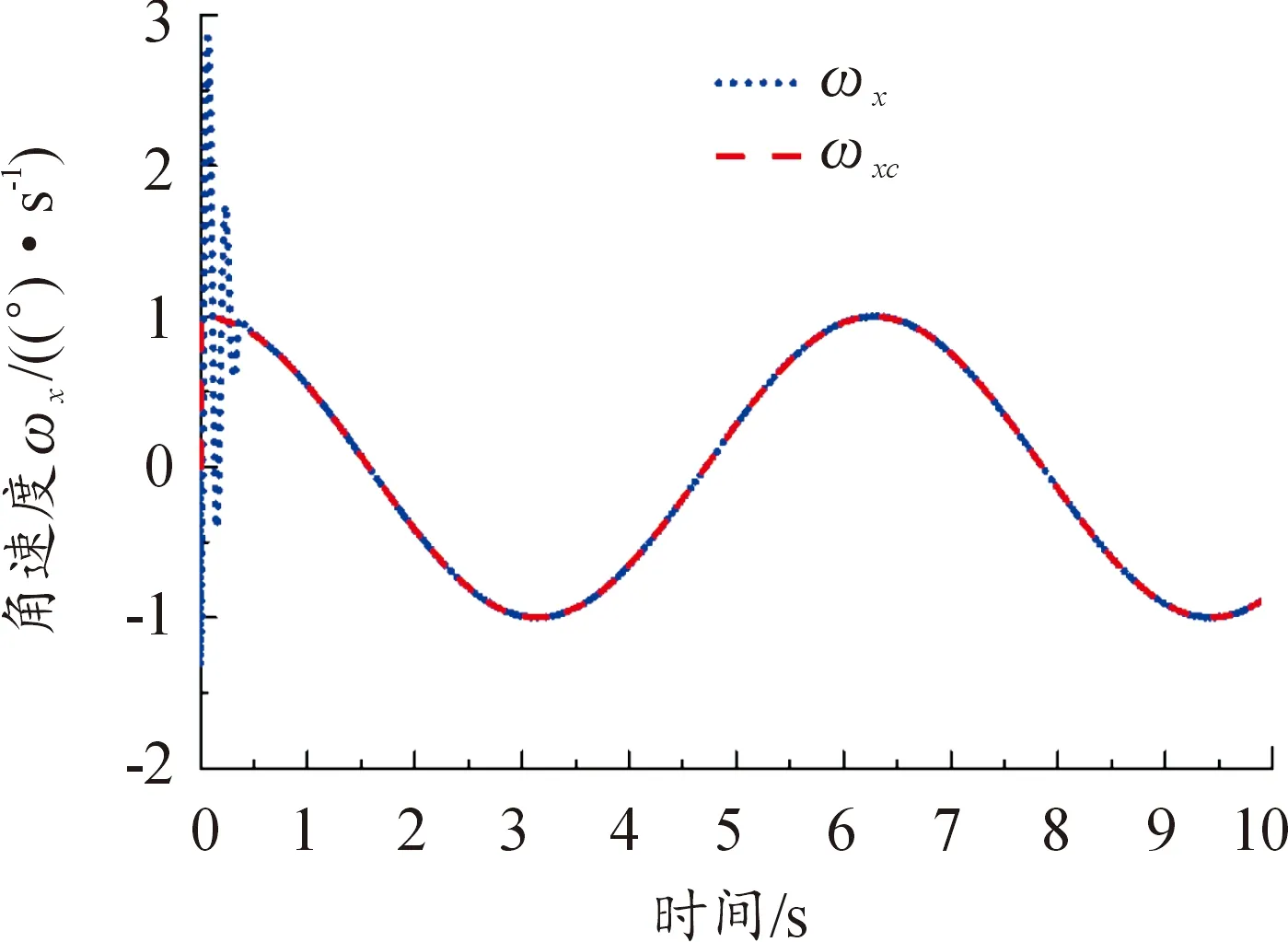
圖3 姿態(tài)角速度指令跟蹤曲線

圖4 控制量變化曲線

圖5 不確定項(xiàng)f(x)估計曲線

圖6 不確定項(xiàng)g(x)估計曲線

為了進(jìn)一步說明所設(shè)計控制器的魯棒性，將偏差加入到系統(tǒng)動力學(xué)模型，并與文獻(xiàn)[19]所設(shè)計的自抗擾控制器進(jìn)行對比，仿真結(jié)果如圖7所示。由圖7可知，當(dāng)系統(tǒng)存在偏差時，采用本文方法控制精度更高，而文獻(xiàn)[19]的方法存在一定偏差，驗(yàn)證了控制系統(tǒng)具有較強(qiáng)的魯棒性。

對舵效不確定情況進(jìn)行仿真試驗(yàn)，假設(shè)舵效附加項(xiàng)為δ(x)=x2-0.2sgn(x2)，動力學(xué)參數(shù)和神經(jīng)網(wǎng)絡(luò)參數(shù)同上，取γ=5，η=3，仿真結(jié)果如圖8和圖9所示。

圖7 2種方法的控制效果對比圖

圖8 姿態(tài)角指令跟蹤曲線

圖9 不確定項(xiàng)δ(x)估計曲線

從圖9可以看出，利用RBF神經(jīng)網(wǎng)絡(luò)對舵效變化帶來的補(bǔ)償項(xiàng)進(jìn)行了較為準(zhǔn)確的估計，從而實(shí)現(xiàn)了舵效不確定情況下的智能補(bǔ)償和自適應(yīng)控制。

5 結(jié)論

本文針對模型大不確定情況設(shè)計了基于RBF神經(jīng)網(wǎng)絡(luò)的智能自適應(yīng)姿態(tài)控制系統(tǒng)，通過理論分析、數(shù)學(xué)證明及仿真驗(yàn)證形成以下結(jié)論：

1) 利用RBF神經(jīng)網(wǎng)絡(luò)能夠解決傳統(tǒng)滑模控制因模型不確定帶來的控制律設(shè)計問題，將RBF網(wǎng)絡(luò)應(yīng)用于滑模控制中能夠?qū)崿F(xiàn)導(dǎo)彈在復(fù)雜戰(zhàn)場環(huán)境下的智能控制。

2) RBF神經(jīng)網(wǎng)絡(luò)具有較強(qiáng)的自學(xué)習(xí)和自進(jìn)化能力，能夠在短時間內(nèi)完成對系統(tǒng)未知量的學(xué)習(xí)與估計，并且估計精度較高，泛化能力強(qiáng)。

3) SMC與RBF網(wǎng)絡(luò)相結(jié)合的智能自適應(yīng)控制系統(tǒng)具有通用化的設(shè)計思想，但是系統(tǒng)穩(wěn)定性對控制參數(shù)的選取具有嚴(yán)格要求，否則難以保證系統(tǒng)穩(wěn)定性。