爆炸沖擊下乘員下肢保護裝置仿生設計與優化

覃凌云,楊書儀,戴巨川,汪國勝,2,李桂兵,凌啟輝,陳哲吾

(1.湖南科技大學 機電工程學院， 湖南 湘潭 411201; 2.中國北方車輛研究所， 北京 100072)

1 引言

現代戰爭中，常常出現非對稱作戰，隨著彈藥和電子技術的發展，地雷和簡易爆炸物爆炸引起的巨幅沖擊已成為軍用裝甲車輛遂行任務時面臨的主要威脅之一[1-2]。而車內乘員下肢作為最先與車輛底部結構接觸的位置，將最先承受地板傳遞而來的劇烈沖擊，因此乘員下肢已成為車輛爆炸事件中最常受傷的部位[3-5]。為減小乘員下肢在戰爭中受到的損傷，國內外學者針對下肢保護開展了深入的研究。在下肢損傷規律和評價指標方面，文獻[6]研究了加速度的持續時間、上升斜率和峰值對乘員小腿損傷的影響。文獻[7]通過跌落試驗和動力學仿真相結合的方法對乘員下肢損傷行為進行了研究，并提出了相對應的損傷評價指標。文獻[8]基于詳細的參數研究，分別采用回歸分析法和響應面法，構建了3種乘員損傷評估回歸模型，并對其預測能力進行了驗證。在下肢保護裝置設計方面，文獻[9-10]結合柔性地板結構和防雷腳墊結構，設計了一種軍用車輛載員下肢保護裝置，并對其結構參數進行了多目標優化。文獻[11]設計了一種雙箭頭負泊松比乘員下肢保護裝置，研究了其幾何參數對其防護性能的影響。

在上述關于下肢保護裝置的研究中，雖然均在車內乘員足部以下100 mm的空間內有效降低了其下肢損傷的風險，但由于車高限制，本文中下肢保護裝置設計空間僅為50 mm，故上述保護裝置難以滿足使用要求。因為仿生結構在吸能能力上優于傳統結構，近年來，采用仿生方法來設計具有優異耐撞性能的薄壁結構的研究逐漸增多，并已廣泛應用于車輛被動安全設計領域[12-14]，但卻鮮有學者將仿生薄壁結構應用于下肢保護裝置的設計中。基于此，本文中采用結構仿生的方式，設計了一種外框為鏤空結構、中間采用仿貝殼薄壁管作為填充的下肢仿生保護裝置(BSPD)。首先，基于乘員約束系統局部等效模型，對不同保護裝置的防護性能進行分析，驗證了仿生設計的可行性；然后，對仿生保護裝置的結構參數進行單因素分析，確定初步設計方案；最后，結合全因子試驗設計法、回歸分析法和NSGA-Ⅱ遺傳算法等方法對保護裝置開展多目標優化，實現對乘員下肢的有效保護。

2 局部等效模型建模與驗證

2.1 乘員約束系統建模

由于本文中的研究對象為乘員下肢保護裝置，為提高工作效率，從整車模型中提取如圖1所示的乘員約束系統局部等效模型。局部等效模型由座椅、下肢保護裝置、安全帶、HYBRID Ⅲ 50分位假人組成。座椅為具有緩沖功能的抗爆座椅，座椅骨架和椅面網格尺寸為5 mm。安全帶采用軍用裝甲車輛常用的四點式安全帶，其中與假人接觸的部分采用2D殼單元模擬，網格尺寸為15 mm，未與假人直接接觸的部分則采用1D 安全帶單元進行模擬。軍用裝甲車輛在受到地雷或簡易爆炸物的爆炸沖擊時，乘員下肢主要受到來自腳部地板傳遞而來的垂向加速度作用。因此，設置邊界條件為座椅安裝處施加6個自由度固定約束，假人腳部地板所有節點上施加如圖2所示的峰值為300g、脈寬為5 ms的三角波沖擊[9,15-16]。

圖1 乘員約束系統模型 Fig.1 Occupant restraint system

圖2 三角波脈沖輸入

2.2 下脛骨力仿真分析與驗證

為了保證假人下肢姿態在加裝保護裝置前后保持一致，在無保護裝置的工況下采用一塊尺寸相同、材料與地板一致的鋼板放在假人腳部。通過LS-DYNA的關鍵字*BOUNDARY_PRESCRIBED_MOTION_SET將作用于地板Z向加速度作為模型的輸入，仿真分析得到假人下脛骨軸向力曲線、盆骨Z向加速度曲線分別如圖3和圖4所示。

圖3 假人下脛骨軸向力曲線 Fig.3 Axial force curves of occupant tibias

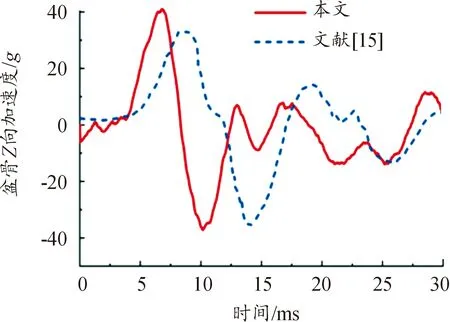
圖4 盆骨Z向加速度曲線

由圖2可知，在峰值300g、持續時間為5 ms的三角波脈沖作用下，假人左右下脛骨力峰值基本一致，分別為14.05 kN和14.30 kN，略小于文獻[9]中的15.29 kN和15.43 kN，其主要原因是：本文中假人小腿姿態與文獻[9]相比，其相對地板的傾斜角較大，來自地板的加速度沖擊沒有垂直作用在假人小腿上；由圖3可知，假人盆骨Z向加速度曲線與文獻[15]在峰值和變化趨勢上均具有較好的一致性。綜上分析，可知本文中建立的乘員約束系統局部等效模型準確性高，用此模型來研究乘員下肢保護裝置具有可信度。

3 乘員下肢仿生保護裝置設計

由2.2節中的分析可知，在爆炸沖擊下，假人下脛骨軸向力已遠超北約NATO AEP-55[17-18]所規定的5.4 kN。因此，為減小乘員下肢在爆炸沖擊下所受的損傷，基于結構仿生原理設計了如圖5所示的乘員下肢仿生保護裝置，其由外框和仿生薄壁管組成，整體尺寸為長寬500 mm×350 mm，高度為50 mm。其中外框側壁設計成波浪形結構，通過影響側壁的可變形剛強度和空間，達到改變外框結構吸能性能的目的；薄壁管采用仿生設計，在軍用車輛受到爆炸沖擊后，主要靠其變形來吸收地板傳遞而來的能量，從而達到保護乘員下肢的目的。

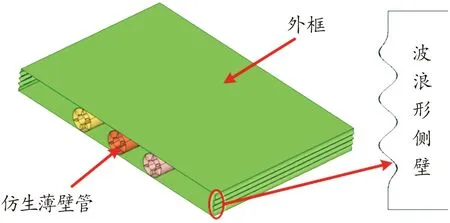
圖5 下肢仿生保護裝置

3.1 仿生薄壁管設計

軟體動物貝殼在其生存過程中，會長期經受環境的考驗，比如：海浪、泥沙等的沖擊和磨損，以及其他動物的攻擊等。其外形截面近似于花瓣形，考慮到貝殼的受載條件后，發現其與薄壁管具有以下相似性：

1) 載荷相似性：在軍用車輛遭遇地雷或簡易爆炸物爆炸時，下肢保護裝置的組成部分薄壁管可能會承受任意方向的沖擊載荷。同樣，貝殼在海洋中生活時，也要面臨來自海水、泥沙及其捕食者在任意方向的沖擊載荷。

2) 功能相似性：下肢保護裝置中的薄壁管，其主要功能是承受爆炸沖擊載荷并吸收沖擊能量，保護乘員下肢不受損傷。而貝殼的主要功能也是承受海水、泥沙及其捕食者的沖擊載荷，保護殼內軀體不受傷害。

根據其相似性，在傳統雙圓管具有良好耐撞性的基礎上，通過增加貝殼形肋骨，設計了一種新型仿貝殼薄壁管，如圖6所示。

圖6 仿貝殼薄壁管

仿貝殼薄壁管的外管、內管及肋骨均采用相同的厚度，其長度L、外管直徑D、內管直徑d、厚度t，分別為100、46、20和0.2 mm。初步設計仿貝殼薄壁管下肢保護裝置的薄壁管排數為3排，肋骨數為6個，“波浪形”外框的厚度為2 mm，外框側壁波峰峰值為2.5 mm。為了驗證仿貝殼薄壁管保護裝置(BSPD)的吸能特性，分別建立與其等質量的傳統雙圓管保護裝置(DCPD)、圓形肋骨保護裝置(CRPD)、仿蝦螯薄壁管[12]保護裝置(BSCPD)、仿竹薄壁管[13]保護裝置(BBPD)及仿馬尾莖薄壁管[14]保護裝置(BHPD)的有限元模型并進行對比分析，如圖7所示。

圖7 6種不同保護裝置有限元模型

下肢保護裝置的基體材料均為T651鋁合金，并采用式(1)所示的Johnson-Cook本構模型[19-20]來模擬其動態力學行為，即：

(1)

采用式(2)所示的損傷模型[19-20]來模擬材料在壓潰過程中的斷裂行為，即：

(2)

式(2)中：εf為斷裂塑性應變；σ*為材料的應力三軸度；D1～D5分別為對應材料的材料參數。T651鋁合金的本構模型和損傷模型對應的參數如表1所示。

表1 T651鋁合金材料參數Table 1 Material parameters of T651 aluminum alloy

通過有限元仿真方式獲取不同保護裝置下假人下脛骨軸向力曲線如圖8所示，下脛骨力峰值和內能對比如表2所示。

圖8 不同保護裝置假人下脛骨力曲線

表2 假人下脛骨力峰值及保護裝置內能對比Table 2 Comparison of occupant tibia peak force and internal energy of protective devices

由圖8可知，與其他5種保護裝置不同的是，在加裝BSPD后，假人下脛骨軸向力在10.3 ms達到峰值后沒有立刻下降而是趨于平穩，這是由于保護裝置在10 ms后仍可發生變形吸收沖擊能量；其中傳統DCPD和CRPD由于整體剛度較弱，在12.5 ms假人下脛骨力達到峰值前已被完全壓潰，不再具備吸收能量的能力；BSCPD和BBPD在假人下脛骨力達到峰值后，雖沒被完全壓潰，但因整體剛度過大，不再發生變形吸收能量。由表2可知，BSPD和BHPD均具有較好的防護能力，但BSPD更優，可將假人左右下脛骨力峰值分別減小為6.43 kN和6.35 kN，小于其他5種下肢保護裝置，且從幾種保護裝置的內能變化量可知，BSPD的內能增加最大為294.36 J，說明其具有最好的吸能效果。綜上可知，BSPD對乘員下肢具有較好的防護效果，下文將以此為基礎展開研究。

3.2 BSPD結構參數分析

3.2.1外框側壁波峰峰值對BSPD防護能力的影響

保持BSPD其他參數不變，考慮到駕駛室空間限制，本文分別取外框側壁波峰峰值1.5、2.5、3.5、4.5 mm及不設置波浪側壁進行仿真分析。其中波峰峰值為2.5 mm與不設置波浪側壁時假人下脛骨軸向力曲線如圖9所示，不同側壁波峰峰值下假人下脛骨軸向力峰值如表3所示。

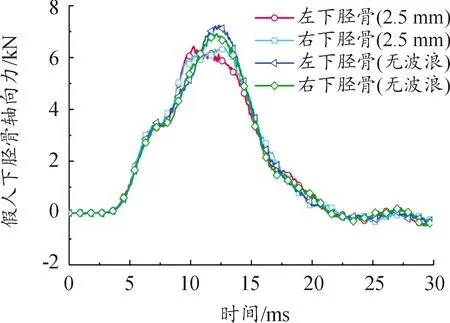
圖9 假人下脛骨力對比曲線

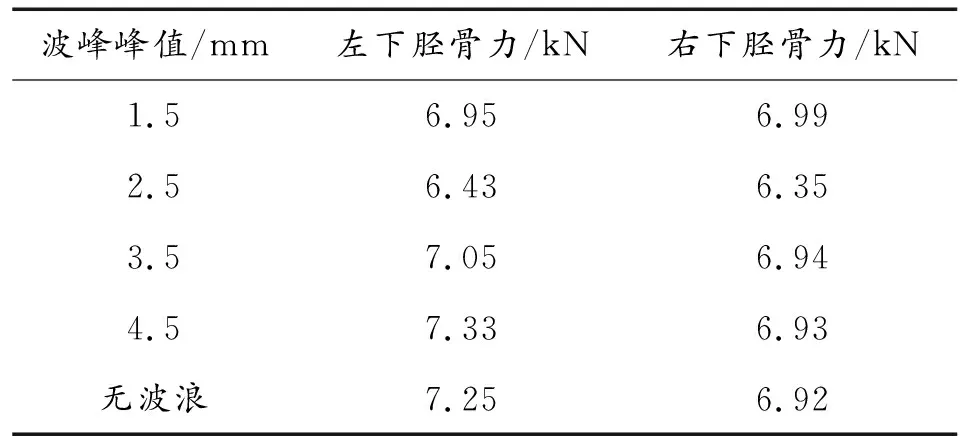
表3 不同波峰峰值假人下脛骨力峰值

由圖9可知，外框側壁為波浪結構相比非波浪結構假人左右下脛骨軸向力峰值分別下降了11.31%、8.24%，說明波浪側壁結構的設計對提升BSPD防護能力具有一定的影響。由表3可知，假人下脛骨軸向力隨著波峰峰值的增大呈先減小后增大的趨勢。波峰峰值通過影響外框側壁變形的剛強度及可變形空間，對BSPD的防護能力產生影響。

3.2.2外框厚度對BSPD防護能力的影響

保持BSPD其他參數不變，本文分別取外框厚度1、2、3和4 mm進行仿真分析，得到不同外框厚度下假人下脛骨力峰值如表4所示。

表4 不同外框厚度假人下脛骨力峰值Table 4 Peak axial forces of tibia for different frame thickness

由表4可知，隨著外框厚度的增加，假人下脛骨軸向力先減小后增大。且當外框厚度在1～2 mm時，假人下脛骨軸向力變化幅度較大，在2～4 mm時，變化幅度較小。說明隨著厚度的增加，外框達到一定的剛度后，其剛度再增大對BSPD的防護能力影響較小。

3.2.3薄壁管排數對BSPD防護能力的影響

保持BSPD其他參數不變，本文分別取薄壁管排數1排、2排、3排和4排進行仿真分析，如圖10所示。由仿真結果可知，隨著薄壁管排數增加，假人下脛骨軸向力呈先減小后增大的趨勢，排數為3排時BSPD防護效果最佳(見表5)。當薄壁管排數為1排和2排時，BSPD整體剛度較弱，使得外框上部與下部發生了撞擊，從而使假人下肢受到的沖擊力較大。而當薄壁管排數為4排時，BSPD整體剛度過盛，增大了其本身對假人下肢的沖擊，故導致4排時假人下脛骨力峰值會略大于3排。

圖10 不同薄壁管排數

表5 不同薄壁管排數假人下脛骨力峰值

3.2.4薄壁管肋骨數對BSPD防護能力的影響

保持BSPD其他參數不變，本文分別取薄壁管的肋骨數4個、5個、6個、7個和8個進行仿真分析。由仿真結果可知，肋骨數量為6個時BSPD防護效果最佳，且隨著肋骨數量增大，假人下脛骨軸向力呈先減小后增大，后逐步平穩的趨勢(見表6)。這是因為當薄壁管肋骨個數較少時，BSPD整體剛度較弱，導致外框上部與下部之間發生撞擊，從而導致假人下脛骨軸向力峰值增大。

表6 不同肋骨數假人下脛骨力峰值Table 6 Peak axial forces of tibia for different rib numbers

3.2.5薄壁管厚度對BSPD防護能力的影響

保持BSPD其他參數不變，本文分別取薄壁管厚度0.15、0.20、0.25、0.30和0.35 mm進行仿真分析。由仿真結果可知，隨著薄壁管厚度的增加，假人下脛骨軸向力呈先減小后增大的趨勢，且在0.15～0.20 mm這個厚度增加時，假人下脛骨軸向力減小幅度最大(見表7)。這是因為在0.15～0.20 mm，存在一個臨界剛度使外框上部與下部剛好不發生撞擊。而當薄壁管厚度為0.15 mm時，BSPD整體剛度較弱，外框上部與下部發生了撞擊，從而導致假人下脛骨軸向力大幅增加。

表7 不同薄壁管厚度假人下脛骨力峰值Table 7 Peak axial forces of tibia for different thickness of thin-walled tubes

3.2.6薄壁管長度對BSPD防護能力的影響

保持BSPD其他參數不變，本文分別取薄壁管長度60、80、100、120和140 mm進行仿真分析。由仿真結果可知，隨著薄壁管長度的增加，假人下脛骨軸向力呈先下降后上升的趨勢(見表8)，且薄壁管長度在100～140 mm變化時，假人下脛骨軸向力峰值變化幅度不大，說明處于BSPD中部的薄壁管對其防護能力的影響較小。

表8 不同薄壁管長度假人下脛骨力峰值Table 8 Peak axial forces of tibia for different length of thin-walled tubes

4 乘員下肢仿生保護裝置優化設計

由上述分析可知，加裝BSPD后，相比于不加裝的情況假人下脛骨軸向力分別下降了50.23%、55.59%，但仍無法滿足AEP-55限值5.4kN的要求。為了進一步提高BSPD的防護能力，對其開展多目標優化設計。首先，確定優化設計變量及其取值范圍，建立優化目標函數及約束函數；然后，基于全因子試驗方法進行試驗方案設計，采用二次多項式建立其回歸模型；最后，運用基于Pareto解的NSGA-Ⅱ算法，求解BSPD的結構參數最優解。

4.1 設計變量和優化目標確定

由3.2節分析可知，外框側壁波峰峰值在上述取值范圍內對BSPD防護性能的影響相對其他參數較小，且考慮到駕駛室空間限制，決定選取峰值為2.5 mm的方案；同時，在薄壁管排數為3排、肋骨數為6個時BSPD具有較好的防護性能，且考慮到這2個參數和薄壁管厚度對其防護能力的影響是相互耦合的，故決定選取薄壁管排數為3排、肋骨數為6個的方案。在上述基礎上，選取外框厚度Tw、薄壁管厚度Tb和長度Lb作為BSPD的優化設計變量，選取假人左右下脛骨軸向力FL和FR作為本次優化的目標函數。同時，考慮到BSPD日常使用的靜剛度要求>200 N/mm，即在與假人腳跟相接觸面上施加1 kN豎直向下的力作用時，BSPD的總變形量應小于5 mm。為了保證BSPD具有足夠的靜剛度，選取其在1 kN作用下的總變形量DS≤3.5 mm作為優化目標函數的約束條件。因此，可建立優化數學模型為：

(3)

4.2 試驗設計

采用全因子試驗設計法提取的信息量非常全面，能較為科學地安排試驗，可估計全部的交互效應及主效應[21]。故本文中采用全因子試驗設計法進行試驗設計，共得到27組采樣點，為了提高回歸模型的預測精度，又增加了13組樣本點，共計40組樣本點，部分采樣點響應值如表9所示。

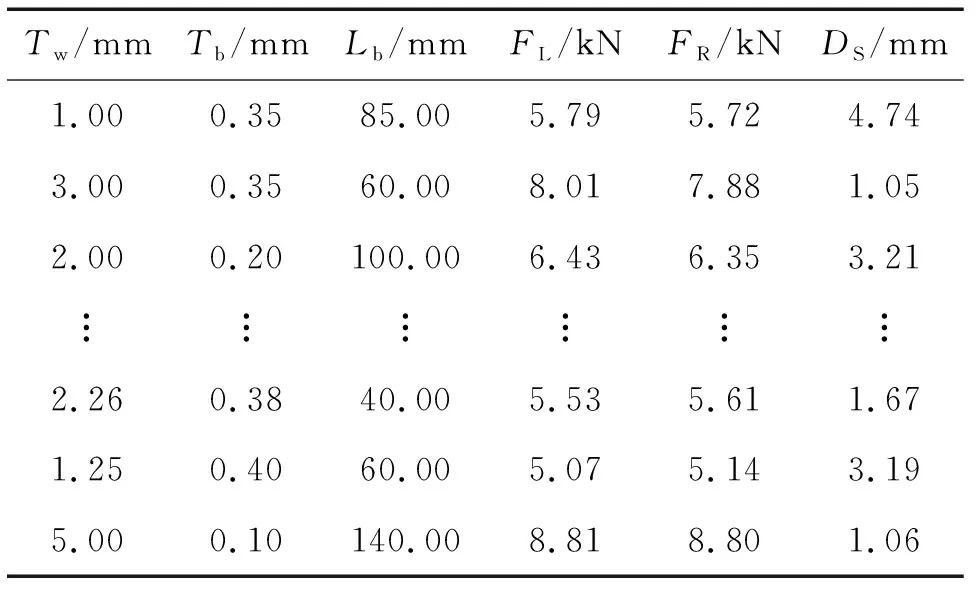
表9 部分采樣點響應值Table 9 Response value for some sampling points

4.3 回歸模型分析

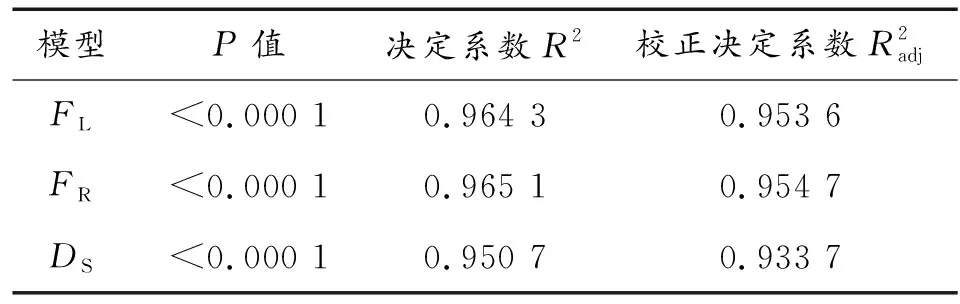
表10 回歸模型顯著性分析Table 10 Significance analysis of regression model

圖11 實際值和預測值對比

4.4 多目標優化

求解多目標優化問題的方法很多，本文采用由NSGA 算法改進而來NSGA-Ⅱ算法[22]，求解式(3)所示的優化數學模型。該算法引入精英采樣策略可避免最佳個體的丟失，通用性強、魯棒性高，可較好地求解多目標優化問題。

本文中設置最大進化迭代次數為100次、交叉概率為0.7、遺傳變異率為0.01，通過尋優得到50組Pareto解(見表11)。考慮到本文優化目標為假人左右下脛骨軸向力最小的條件下，保護裝置總變形滿足設定要求即可，通過比較發現第14組解的FL、FR最小，故選擇第14組解為本次優化問題的最優解。

表11 部分Pareto解集Table 11 Part of Pareto set

為了驗證優化結果的準確性，將上述優化參數代入仿真模型并進行計算，得到優化值與仿真值的相對誤差如表12所示。由表12可知，優化值和仿真值具有高度一致性，相對誤差均在4%以內，說明優化設計方案是真實可信的。

表12 優化值和仿真值對比Table 12 Comparison of optimized and simulated values

將加裝優化后BSPD的仿真結果與優化前進行對比，得到假人下脛骨軸向力曲線和BSPD變形云圖分別如圖12和圖13所示。

圖12 優化前后假人下脛骨力曲線

由圖12可知，在優化后假人左右下脛骨力峰值分別由6.43 kN和6.35 kN減小到4.67 kN和4.83 kN，均滿足AEP-55限值5.4kN的要求，且分別降低了27.37%、23.94%。

圖13 BSPD變形云圖

由圖13可知，在優化后BSPD的總變形量由3.21 mm減小到3.16 mm，靜剛度達到316.46 N/mm，滿足日常使用靜剛度>200 N/mm的要求。說明優化效果良好，優化后的BSPD可對乘員下肢進行有效防護。

5 結論

1) 提出了一種仿貝殼薄壁管下肢保護裝置(BSPD)，并與加裝DCPD、CRPD、BSCPD、BBPD及BHPD等5種保護裝置下假人下脛骨軸向力、結構內能變化量進行了對比分析，初步驗證了BSPD具有良好的防護性能。

2) 加裝優化后的BSPD可在乘員足部以下50 mm的空間內對乘員下肢進行有效防護，與未加裝前相比，加裝優化后的BSPD時假人左右下脛骨軸向力峰值分別降低了66.76%和66.22%。

3) 本文中通過結構仿生來設計乘員下肢保護裝置的思路是可行的，有效降低了乘員下肢損傷的風險，可為其他乘員下肢保護裝置的設計提供方向。