基于滑模控制的無人駕駛自行車設計與仿真

劉佩佩，周亞麗，張奇志

(北京信息科技大學自動化學院，北京 100192)

1 引言

自行車是日常生活中非常普遍且通用的兩輪交通工具，具有靜態不穩定和動態可穩定特性。因此自行車已經成為一種對平衡性與穩定性分析和研究的重要實驗平臺。

1899年Whipple[1]首次運用數學方程描述了自行車的運動行為，并提出了自穩定的概念。自此之后，隨著計算機時代的到來，越來越多的研究者借用計算機仿真等工具對復雜問題進行仿真和分析，由此開始了對無人駕駛自行車的深入研究。郭磊，黃用華等人[2-3]基于部分反饋線性化原理，以各自所設計的試驗樣機為平臺，實現了多種無人駕駛自行車的平衡運動。Shafiekhani[4]等人采用了基于神經模糊控制器的無人駕駛自行車平衡控制方法，獲得了較好的控制效果。2019年，清華大學類腦計算研究中心施路平教授團隊在《自然》上發表的文章中，搭載天機芯的無人駕駛自行車也瞬間火爆網絡[5-6]。2020年，劉延柱教授[7]討論了無人駕駛自行車穩定行駛的實現可能性，對前叉受控的自行車數學模型做了穩定性分析，進一步表明前叉轉軸系統對自行車穩定性的重要影響。

總結前人的研究經驗，本文從自行車前叉轉向系統的設計出發，設計一種基于曲柄滑塊機構控制的無人駕駛自行車，實現了對轉向電機輸出力矩的放大作用，并通過設計滑模控制器對系統進行了仿真驗證。

2 系統動力學模型建立

2.1 無人駕駛自行車系統描述

圖1所示為無人駕駛自行車系統結構模型圖。假設系統所有的質量集中于質心上，定義質心高度為h，質心在水平面上的投影點與后輪著地點的距離定為b，前輪質心到前車把轉動軸的距離為λ，車身與z軸的夾角為車體傾角β，前車把轉軸與x軸的夾角為前車把轉角δ，定義逆時針方向為正方向。定義車體傾角和前車把轉角均為零時的滑塊位置為起始位置；起始位置時曲柄滑塊機構可看成是一個直角三角形，定義直角短邊、即曲柄為c(始終與前車把保持平行共面)，直角斜邊、即連桿為a，這兩條邊的長度為定值、可測量；定義滑塊位置邊長度為x。系統啟動瞬間，自動調整配重塊位置，保證車體處于直立平衡狀態。

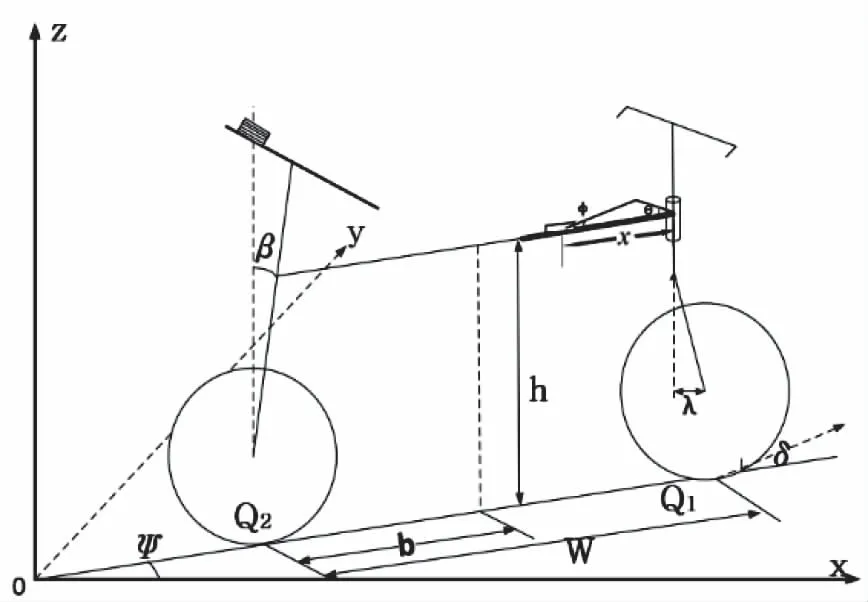
圖1 無人駕駛自行車系統結構模型

圖2所示為本文所用的無人駕駛自行車試驗樣機，遵循日常自行車前輪轉向、后輪驅動的特性，由一輛常規自行車安裝曲柄滑塊機構裝置、配重調節機構和電控系統等改造而來。其相關物理參數如表1所示。

表1 無人駕駛自行車的相關物理參數

2.2 曲柄滑塊機構描述

2.2.1 曲柄滑塊機構運動分析

記曲柄AB的長為c，連桿BC的長為a，滑塊的位置相對A點的長為x，曲柄與滾珠絲杠滑臺的夾角即曲柄轉角為θ，連桿與滾珠絲杠滑臺的夾角即擺角為φ；在對系統進行建模時，將曲柄看為車把的一部分，將連桿看為車架的一部分，忽略滑塊的重量和其運動過程中所受到的摩擦力。

圖3 曲柄滑塊機構模型簡圖

由圖3所示，利用三角關系，滑塊位置x可表示為

(1)

對模型進行近似化

(2)

由圖1可知，δ=90°-θ，代入式(2)得

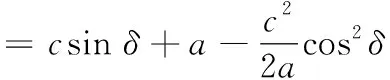
(3)

2.2.2 曲柄滑塊機構受力分析

對于自行車轉向系統的設計來說，傳統的方法是直接將轉向電機安裝在前車把轉軸上，而本文所設計曲柄滑塊機構控制車體轉向的方法，巧妙地運用了杠桿原理，相當于對力臂進行了延長，在轉向電機輸出同樣力矩的情況下，前車把可以獲得的力矩更大。如圖4為滑塊受力分析圖。

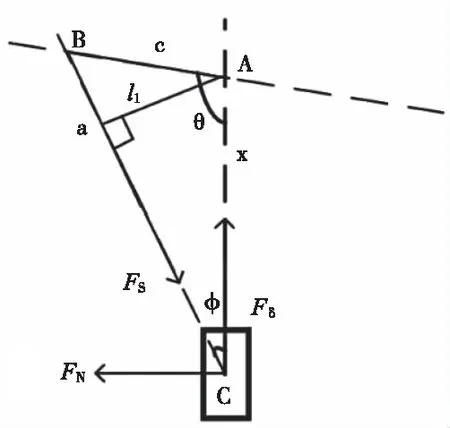
圖4 滑塊受力分析圖

在圖4中，Fδ為轉向電機對滑塊的輸出推力，FN為滑臺對滑塊的擠壓力，Fs為滑塊作直線往復運動時連桿對滑塊的推力，l1為轉向過程中的力臂。由圖4可知，根據力的分解及做功原理，Fδ和Fs的關系式可表示為

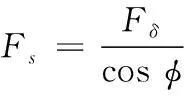
(4)

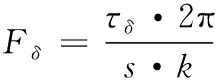
(5)

式中，τδ為轉向電機輸出力矩，s為滾珠絲杠螺距，k為同步增速比。

結合式(4)和式(5)可得：

(6)

在ΔABC中，利用等面積法可得

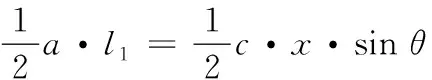
(7)

將表1的實際參數值代入式(6)和式(7)，整理可得前車把轉軸上受到的力矩τf為

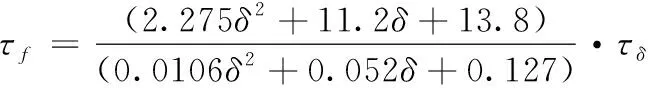
(8)

圖5所示為力矩放大倍數與前車把轉角關系的變化曲線。可以看出，曲柄滑塊機構對轉向電機輸出力矩的放大倍數在56～144范圍內。

圖5 力矩放大倍數與前車把轉角變化曲線

2.3 拉格朗日方程法建立動力學模型

對圖2所示的無人駕駛自行車，分為前車輪、后車輪、車架、前車把四個部分。并作如下合理化假設：前后輪質心均位于其圓心處；車把質心位于車把正中心，車架質心位于其質量中心，忽略曲柄滑塊機構的質量。

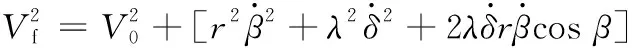
(9)

前輪動能為

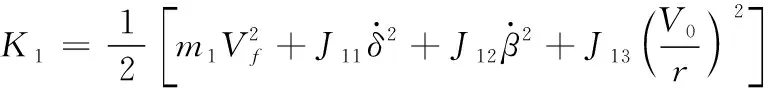
(10)

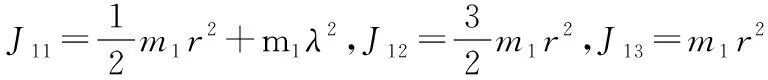
前輪勢能為：

P1=m1grcosβ

(11)

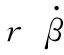
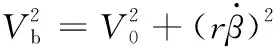
(12)

后輪動能為

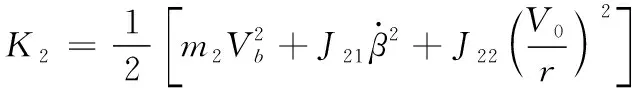
(13)

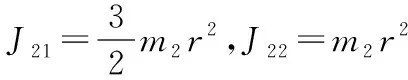
后輪勢能為

P2=m2grcosβ

(14)

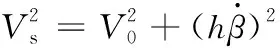
(15)

車架動能為

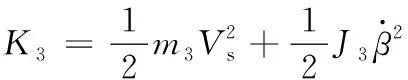
(16)

其中：J3=m3h2

車架勢能為

P3=m3ghcosβ

(17)

(18)

車把動能為

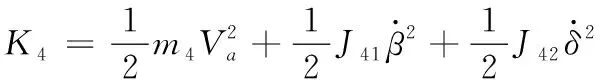
(19)

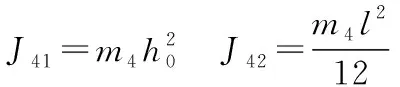
車把勢能為

P4=m4gh0cosβ

(20)

將上式進行相加，分別得系統總動能和總勢能

K=K1+K2+K3+K4

P=P1+P2+P3+P4

(21)

根據第二類拉格朗日方程，代入Lagrange方程L=K-P

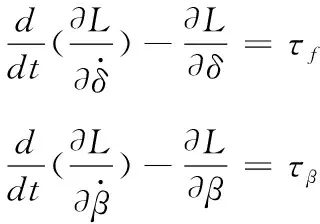
(22)

經整理可得，系統線性化動力學模型為

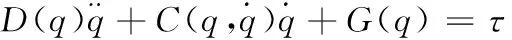
(23)

式中

3 滑模控制器設計

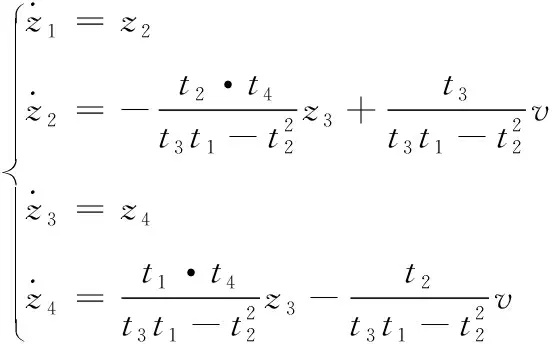
(24)

其中

t4=(m1gr+m2gr+m3gh+m4gh0)v=τf

首先進行誤差方程的設計與分析，取

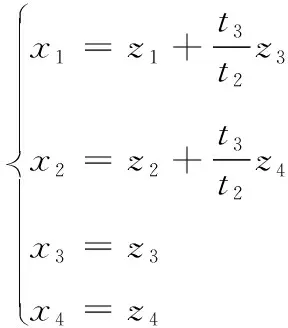
(25)

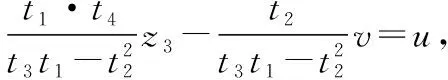
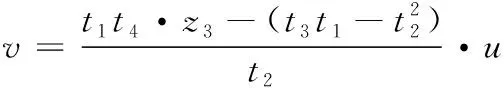
(26)

則有

(27)

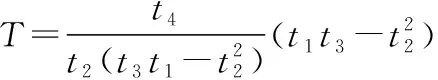
要使式(27)所示的系統穩定，f1需滿足如下三個假設條件[8]：

假設1：f1(0，0，0)=0；

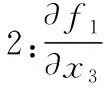
假設3：如果f1(0，0，x3)→0，則x3→0。

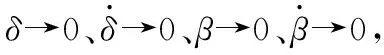
(28)

取滑模函數為

s=c1e1+c2e2+c3e3+e4

(29)

由式(29)可知

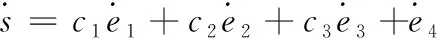
(30)

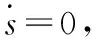
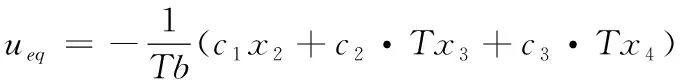
(31)

(32)

u=ueq+usw

(33)

4 仿真分析

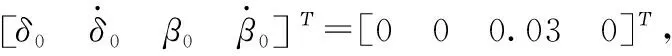
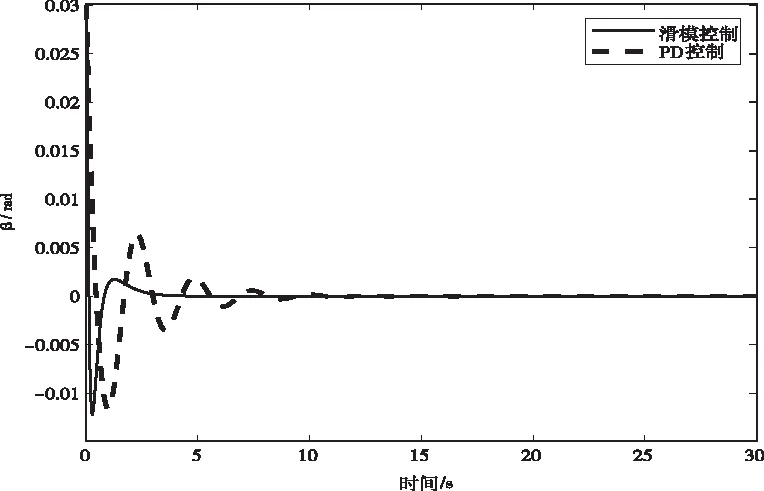
圖6 車體傾角變化曲線

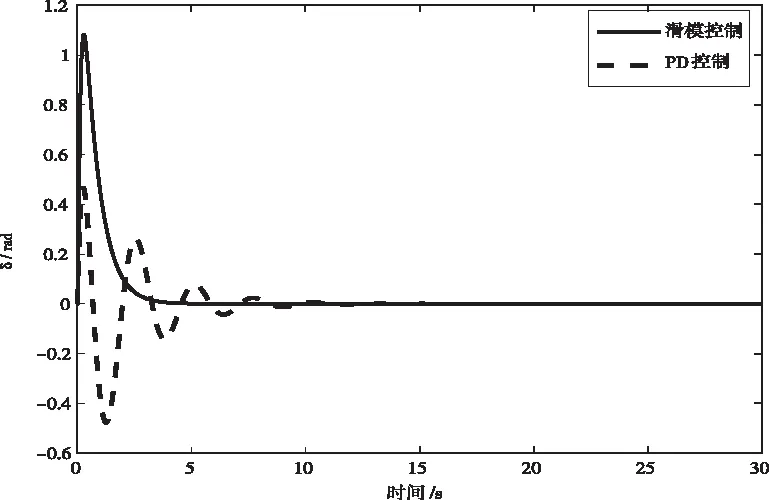
圖7 前車把轉角變化曲線

圖8 轉向電機輸出力矩曲線

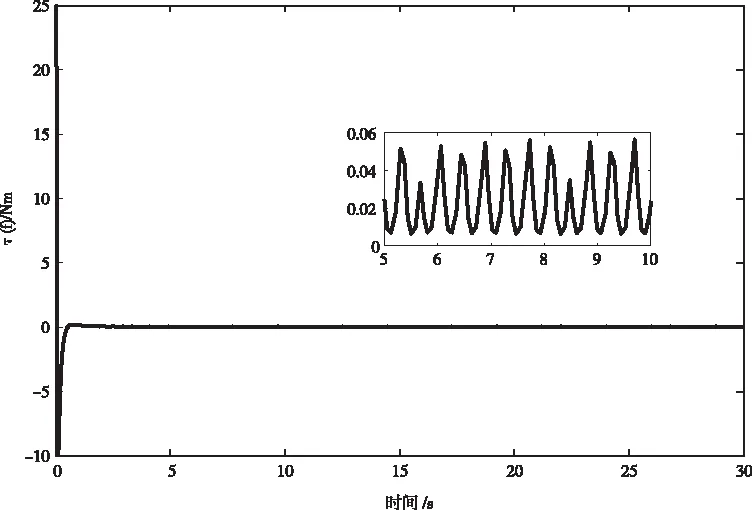
圖9 前車把轉軸力矩曲線

由圖6和圖7可知，系統起始處于向左傾斜0.03rad的不平衡狀態，在控制器的作用下，前車把轉角迅速向左轉，在大約2s后，又迅速向右調節。對于PD控制器，大約10s后，車體傾角基本調節到平衡位置，前車把由于慣性作用，大約在13s后到達平衡位置；與PD控制器相比，滑模控制器所需的調節時間大大縮短，整個系統的調節過程大約只需3s，且曲線的整體變化趨勢更加平穩。從圖8和圖9可以看出，在初始時刻，轉向電機輸出力矩急速增大，大約為0.24N.m，經曲柄滑塊機構的放大，前車把轉軸上獲得的力矩為25N.m，在2s后，前車把轉軸上的力矩保持在0到0.06N.m范圍內維持一種動態調節狀態。根據人的駕駛經驗，當車體傾倒時，人總是本能的先將前車把向車體傾倒的一側轉動，等不再有繼續傾斜的趨勢后，再反向轉動車把，使車體回到平衡位置，因此整個調節過程符合人們騎車的經驗。

5 總結

本文設計和實現了一種基于曲柄滑塊機構控制的無人駕駛自行車，以及這種系統實現直立平衡運動的滑模控制器設計與仿真。仿真結果表明，文中所采用的控制方法可以在轉向電機輸出很小力矩的情況下在很短時間內實現無人駕駛自行車系統的直立平衡運動，為進一步開展無人駕駛自行車平衡運動控制以及路徑規劃等奠定了基礎。