基于CFD的靶機外掛曳光管氣動特性研究

陳亞洲，焦 陽，李哲，韓林軍

(1.中國人民解放軍95821部隊，甘肅酒泉 735000；2.空軍工程大學航空工程學院，陜西西安 710038)

1 引言

靶機作為一種動態實物航空模擬器，在地空導彈武器系統靶場試驗中扮演著“藍軍”角色，廣泛應用于地空導彈武器系統性能試驗、鑒定、效能評估，以及部隊作戰訓練和演習演練任務[1]。在控制試驗成本的前提下，為了滿足于試驗需求，靶機普遍采用小尺寸、輕質量設計，因此其紅外特性較弱，與真實目標差距較大，難以滿足紅外制導武器系統試驗、靶場光學測量設備試驗需求，需采取一定技術手段對靶機的紅外特性進行增強。在靶機上加裝紅外噴燈和紅外曳光管是兩種常用的紅外特性增強技術[2-3]，例如諾斯羅普公司通過在其研制的Chukar靶機上采用紅外噴燈的方式加裝紅外拖靶，以改善其紅外特性；南京航空航天大學無人機研發團隊則在“長空”系列靶機上加裝曳光管，以增強靶機紅外特性，上述兩種技術均是采用燃燒法增加靶機的總體紅外輻射特性，均取得了不錯的效果，得到了廣泛應用。在靶機上掛載曳光管，雖然可以有效增強其紅外特性，但曳光管的掛載會對靶機的氣動特性產生影響[4]，直接影響靶機的飛行速度。因此，本文采用計算流體力學(Computational Fluid Dynamics，CFD)方法，對曳光管不同掛載方式下靶機氣動特性進行分析，研究不同高度條件下曳光管掛載前后、不同掛載數量、不同掛載方式下靶機氣動特性的變化規律，從而獲取曳光管最優掛載方式，為靶機掛載曳光管等外掛設備提供一定的理論指導和數據支撐。

2 靶機三維建模與網格劃分

目前靶場靶機掛載曳光管后一般只進行靶機重心測量和推力線調整，對靶機氣動特性一般不做測試。若進行風洞實驗分析氣動特性需要耗費較大的經費，若不進行氣動特性分析，難以確定亞音速靶機掛載曳光管最佳方式，無法使亞音速靶機掛載曳光管后飛行性能最優。CFD是現代流體力學的一個重要的分支，它融合了流體力學、計算數學、計算機科學等多種學科，發展成為一門新興學科[5]。CFD與傳統的風洞實驗相比，不僅提高了設計效率，縮短了研制周期，節約了研制成本，而且解決了以往風洞實驗、飛行試驗無法模擬的難題[6]。本文通過CFD方法計算不同曳光管掛載方式對亞音速靶機阻力和平飛速度的影響程度，為合理確定曳光管掛載方式提供理論依據。

在利用CFD方法計算時，首先，建立亞音速靶機三維幾何模型，然后，對幾何模型進行網格劃分，最后，求解該模型的納維-斯托克斯(N-S)方程。

2.1 靶機三維幾何模型建立

本研究以國產某型亞音速靶機為研究對象，該靶機機長4.14m，翼展1.732m，機翼面積0.8m2；曳光管直徑61mm，長度267mm，為減小曳光管風阻，在曳光管頭部加裝65mm長的橢球形整流罩，曳光管掛載在機翼下距機身10cm處。在建立飛機表面幾何模型時，主要采用CATIA中的創成式外形設計方法，其中曲面設計運用了多截面曲面、橋接曲面、填充曲面等。根據亞音速靶機外形和曳光管外形數據，建立了1：1比例的CATIA模型，如圖1所示。本文主要研究曳光管不同掛載數量和掛載方式對亞音速靶機飛行阻力及平飛速度的影響，以靶場試驗任務中常見的左右各掛載1枚和4枚曳光管、掛載方式為翼下和翼尖作為輸入條件對不同條件下靶機的氣動特性進行研究。

圖1 靶機掛載曳光管CATIA模型

2.2 幾何模型的網格劃分

圖2 亞音速靶機掛載曳光管剖面網格

網格劃分的質量會對CFD精度和速度產生至關重要的影響[7]。Pointwise是一款采用T-Rex網格技術對非常復雜的幾何模塊快速生成具有邊界層的體網格，且其邊界層向主流區的網格均勻過渡的軟件[8]。采用Pointwise軟件直接讀取亞音速靶機三維CATIA模型并進行網格劃分，其剖面網格如圖2所示。為保證網格質量，需要細化處理影響氣動特性的關鍵部位，從圖2中可以看出機翼附近網格細密，網格質量好，而機身位置物理量變化不大，為了節約計算時間只進行了粗化處理。亞音速靶機流動左右對稱，故采用半模計算方法，剖面網格圖中紅色為四面體網格，藍色為棱柱網格，綠色為表面網格，黃色為五面體網格。為說明網格疏密對數值模擬結果的影響，構建了密、中、疏三套網格進行無關性驗證，以氣動力量值作為網格無關判定依據。當半模網格總量約為230萬時，與風洞試驗數據相比較，數值計算的結果能夠保持較高精度，且能保證近壁面y+≤1。

3 流場的求解

3.1 控制方程

不考慮體積力及外部熱源，直角坐標系下三維非定常可壓縮納維-斯托克斯(N-S)方程組為

(1)

其中

式中Q為守恒變量，F、G、H分別為直角坐標系下x，y，z三個方向上的無粘通量，Fv、Gv、Hv分別對應三個方向粘性通量。ρ為密度，p為壓力，T為溫度，u、v、w為對應的速度分量。粘性應力τij(i=x，y，z；j=x，y，z)為黏性應力張量的分量，e為單位質量氣體總內能，ht為單位質量氣體總焓，k為流體的傳熱系數。

為使方程封閉，引入理想氣體狀態方程。壓力p可通過該方程計算得到

(2)

其中γ為等熵指數(絕熱指數)，R為氣體常數。

3.2 數值計算方法與可信度驗證

CFD計算的核心便是對N-S方程的求解[9]，通過網格劃分將流場空間進行離散化處理，將偏微分方程轉化為代數方程組。N-S控制方程的離散和求解大致有三種方法，分別是有限差分法、有限元法和有限體積法。本文采用有限體積法進行求解，基于雷諾平均(RANS)方法對進行掛載曳光管的亞音速靶機進行了氣動力計算，其中湍流模型采用k-ω-SST模型。

采用ANSYS Fluent軟件進行流場計算。Fluent軟件是一款優異的CFD求解器，在飛行器空氣動力學領域得到了廣泛的應用[10]。在使用Fluent軟件進行求解時還需要進行一些關鍵的模型和邊界條件的設置，本文采用理想氣體模型進行定常穩態求解，同時設置遠場邊界條件和壓力出口邊界條件。

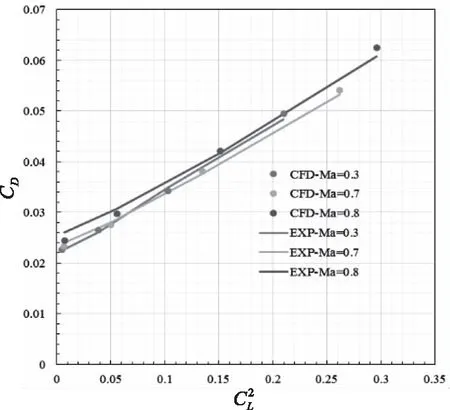
圖3 CFD計算與風洞實驗 數據對比

4 結果分析

4.1 不同掛載方式對靶機阻力影響

以亞音速靶機平飛速度0.7Ma為例，曳光管掛載數量為左右各1枚和4枚，掛載方式分別為翼尖和翼下，分析曳光管掛載方式對亞音速靶機全機阻力的影響，計算結果如圖4所示。從圖中可以看出亞音速靶機掛載曳光管后阻力明顯增加，左右各掛載4枚曳光管時阻力明顯大于左右各掛載單枚曳光管情形；相同掛載數量的情況下，翼尖掛載時阻力小于翼下掛載時阻力。

當翼尖左右各掛載1枚曳光管時，亞音速靶機阻力系數相對于空載狀態增加6.81%，當翼下左右各掛載1枚曳光管時，亞音速靶機阻力系數相對于空載狀態增加8.64%；當翼尖左右各掛載4枚曳光管時，亞音速靶機阻力系數相對于空載狀態增加了33.18%，而當翼下左右各掛載4枚曳光管時，亞音速靶機阻力系數相對于空載狀態增加了36.36%。具體擬合結果見表2。

圖4 四種掛載方式的 曲線圖(Ma=0.7)

表1 數據擬合結果(Ma=0.7)

4.2 不同掛載方式靶機最大平飛速度

根據曳光管的不同掛載方式下靶機的阻力系數增量分別計算了原始狀態及四種掛載方式亞音速靶機在不同高度下的最大平飛速度。亞音速靶機在某一飛行高度以最大速度平飛時，發動機最大推力Tmax等于靶機阻力D，該型渦噴發動機在不同高度下的最大推力根據出廠情況已知。最大平飛速度的計算公式為

(3)

(4)

其中：ρ是空氣密度，CD是阻力系數，S是機翼面積。

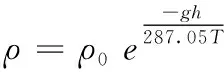
(5)

T=T0-0.0065h(h<11000m)

(6)

上式中T0=288.15k，ρ0=1.225 g/cm3，g=9.8067 m/s2。

由此可得到最大平飛馬赫數為：

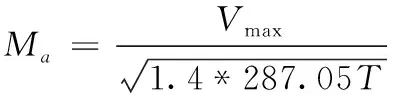
(7)

根據上述公式，獲得靶機在空載以及四種曳光管掛載方式下，不同高度的最大平飛速度如圖5所示。從圖5中可以看出在海高0～10000m范圍，隨著高度的增加，無論是否掛載曳光管，亞音速靶機最大平飛速度均呈現先增大后減小的過程；受發動機最大推力隨高度變換以及空氣密度、阻力系數等綜合影響，在海高4000m或5000m時亞音速靶機平飛速度最大，這一數據也為靶機最大平飛速度提供了理論值；亞音速靶機掛載曳光管后在不同高度下的最大平飛速度均有下降，其中左右各掛載4枚曳光管的最大平飛速度均小于左右各掛載1枚曳光管的情況，而相同掛載數量情況下，曳光管掛載于翼下對靶機平飛速度影響更大。

在海高10000m時，亞音速靶機空載時最大平飛速度為0.752Ma，翼尖和翼下對稱掛載1枚曳光管時最大平飛速度分別為0.723Ma、0.716Ma，最大平飛速度分別減少了3.9%和4.8%，而翼尖和翼下對稱掛載4枚曳光管時最大平飛速度分別為0.627Ma、0.621Ma，最大平飛速度分別減少了16.6%和17.4%。

圖5 亞音速靶機曳光管不同掛載方式最大平飛速度

從圖5看，將相同數量的曳光管掛載在翼尖位置時，靶機的最大平飛速度要明顯大于掛載在翼下位置時的最大平飛速度。這是由于將曳光管掛載在翼尖位置時，其功能相當于“翼尖小翼”。靶機在飛行時，由于機翼上下表面壓差的存在，翼尖附近機翼下表面空氣會繞流到上表面，形成翼尖渦，致使翼尖附近區域機翼上下表面的壓差降低，從而導致這一區域產生的升力降低。而在翼尖處掛載曳光管能夠有效阻礙上下表面的空氣繞流，降低了因翼尖渦造成的升力誘導阻力，減少繞流對升力的破壞，提高了升阻比。而將曳光管掛載在翼下位置時，不能起到上述作用，卻增加了誘導阻力，導致整體阻力增大，使最大平飛速度減小。因此在飛行試驗要求靶機具有較大的平飛速度時，宜考慮將曳光管掛載在翼尖位置。

5 總結

本文采用計算流體力學的方法，對不同掛載方式、掛載不同數量曳光管靶機的機體阻力及最大平飛速度進行研究分析，獲得結論如下：靶機掛載曳光管后其氣動阻力顯著增加，且氣動阻力隨著曳光管數量的增加而增大，翼尖掛載對靶機氣動阻力的影響小于翼下掛載，該研究成果為靶機改裝設計提供理論指導和數據支撐。與此同時，上述計算模型和計算方法也可推廣至箔條彈、龍伯球等其它任務設備掛載對靶機飛行性能的影響分析與計算之中，具有較好的適用性。