基于門控循環單元的移動社會網絡鏈路預測方法

劉林峰 于子興 祝賀

（南京郵電大學計算機學院 南京 210023）

隨著時代的進步，網絡的概念逐漸多元化，衍生出如互聯網、物聯網、經濟網絡、生物網絡等各種網絡形式.在現實世界中，網絡扮演著重要的角色，網絡可以將現實世界中的具體問題抽象描述為一個復雜的網絡系統.網絡可以分為靜態網絡和動態網絡2 類，現實世界中絕大多數網絡都屬于動態網絡，這些網絡中的節點、鏈路都會隨著時間的推移而消失或出現.此外，網絡中鏈路代表著不同實體之間產生的行為或者偏向，所以分析并預測這些網絡中的鏈路具有重要的意義.

網絡的鏈路預測通常是指預測網絡中節點之間的潛在關系，如何提高預測性能一直是網絡科學的一個挑戰.性能優異的鏈路預測方法能夠更好地理解網絡的演變，從網絡中提煉出更有價值的信息，比如蛋白質相互作用網絡中[1]，酵母菌與蛋白質之間80%的相互作用不為人知，如果在已知網絡結構的基礎上設計足夠精確的鏈路預測方法再進行預測指導實驗，就能夠提高實驗成功率、降低測試成本.

移動社會網絡[2]是一種典型的動態網絡，如果將網絡映射到圖中，則節點代表人或實體，鏈路代表節點間的聯系.由于這種聯系具有時間特征，所以導致了網絡的高度動態性和復雜性.

移動社會網絡的鏈路預測可以預測人與人之間的交互，分析這種交互可以一定程度上得知一個人的交往或性格傾向，甚至能夠判斷該用戶可能需要的服務.比如出租車司機可以更加容易在合適的地點找到乘客，陌生人之間更容易找到意氣相投的朋友，賣家能夠更加精準地為買家提供他們所需的商品.精準的鏈路預測能夠為移動社會網絡降低資源開銷，給人們的生活帶來極大的便利.圖1 為一個移動社會網絡示意圖，比如在道路上用戶通過藍牙或車載局域網絡進行通信，在小區里人們使用智能設備接入WiFi 信號點進行信息交互，也可以通過無線信號接入互聯網并連接服務器，由服務器來控制用戶之間的通信.

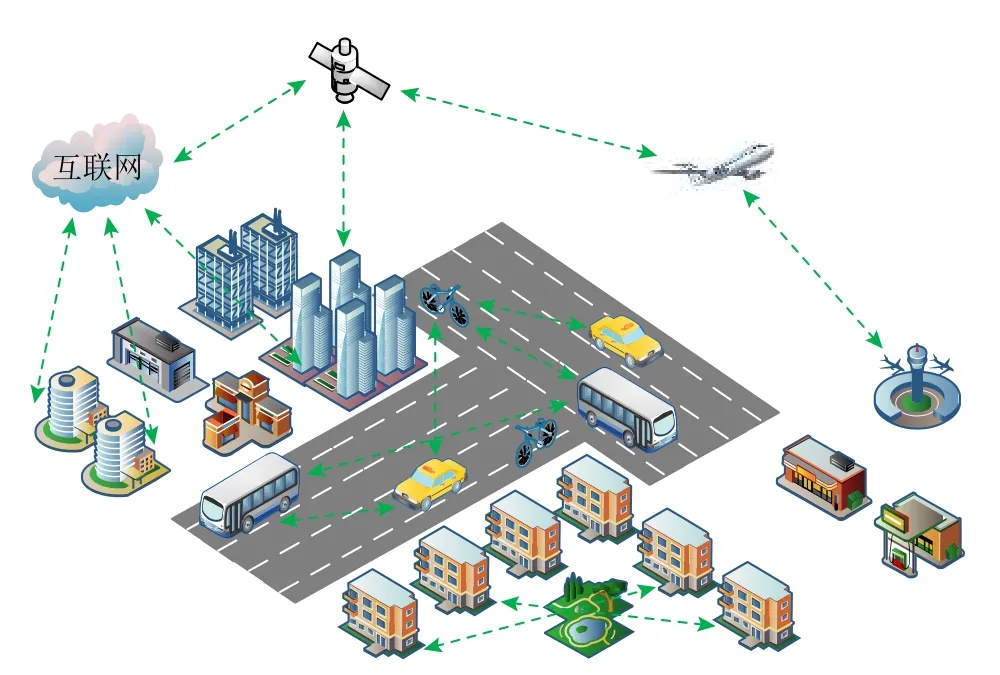
Fig.1 Example diagram of mobile social network圖1 移動社會網絡示意圖

1 相關工作

鏈路預測的目的在于根據網絡的歷史信息來預測未來的網絡結構，這可以更好地理解網絡的演變，發掘網絡中有價值的信息.

目前，鏈路預測方法主要分為3 種：基于節點相似性的鏈路預測方法、基于矩陣分解的鏈路預測方法、基于機器學習的鏈路預測方法.

1.1 基于節點相似性的鏈路預測方法

基于節點相似性的鏈路預測方法是指基于網絡中節點的結構信息、屬性信息和行為去評估節點間的相似度，若節點間的相似度越高，則表明該對節點越相似，即產生鏈路的可能性越大.

目前廣泛應用于靜態網絡的鏈路預測指標有很多，例如共同鄰居算法（common neighbors,CN）[3]、資源分配指標（resource allocation index,RA）[4].在此基礎上，文獻[5]基于節點相似性算法和事件檢測算法提出一種社會網絡事件鏈路預測方法，該方法對不同網絡的演變性進行統一評價，并依此建立事件檢測模型，并利用該模型完成鏈路預測.文獻[6]提出了基于節點度和聚類系數的共同鄰居緊密度指數，認為節點的共同鄰居之間的關系越緊密，節點間連接的可能性就越高.文獻[7]考慮了用戶活動和其共同的鄰居，并定義了局部和全局鏈路預測算法對節點之間的相似度進行評估.文獻[8]重點關注了鏈路方向在鏈路預測問題中的作用，認為雙向鏈路可能包含更多的網絡信息，并發現具有雙向鏈路的小部分節點更有可能通過雙向鏈路連接到共同的鄰居.文獻[9]認為現有的計算節點相似度方法中公共鄰居的數量只描述了一種定量關系，沒有考慮給定網絡的拓撲結構，于是引入節點度的概念和社區結構的思想，提出了局部親和結構，然后與其他相似度指標在不同網絡中進行實驗，最終提高了鏈路預測精準度.

文獻[3-9]中的預測方法主要在拓撲變化緩慢或發生變化較少的網絡中性能較好，因此當應用場景中網絡結構隨時間頻繁發生變化時，預測效果大大削弱.

1.2 基于矩陣分解的鏈路預測方法

基于矩陣分解的鏈路預測方法是指利用矩陣分解得到的低秩矩陣來解決鏈路預測問題.其中，矩陣通常由鄰接矩陣或提取的其他網絡結構信息矩陣組成.目前，矩陣分解主要有奇異值分解、非負矩陣分解和概率矩陣分解.

文獻[10]提出了一種動態網絡的鏈路預測方法，該方法從第一張網絡快照中得到特征矩陣，并求解其低秩矩陣.然后，根據后續網絡快照不斷更新低秩矩陣，最終利用差值估算未來時刻節點之間鏈路的可能性.文獻[11]指出，現有的鏈路預測算法缺乏對社會信息網絡中的拓撲信息和非拓撲信息的有效融合，因此基于用戶主題信息定義了用戶主題相似度指數，并基于該指數構造主題相似度矩陣，然后將目標網絡的信息和主題相似度矩陣融合到概率矩陣分解框架中，并在此基礎上得到網絡節點的表示，最后根據得到的隱含特征表示計算網絡節點之間產生鏈路的概率.文獻[12]將動態網絡結構隨時間變化的特性融合到非負矩陣分解中，提出了一種非負矩陣分解迭代規則，然后根據矩陣分解的結果得到網絡的相似度矩陣，從而完成了鏈路預測.文獻[13]采用非負矩陣分解的方法提取了時間序列圖的潛在特征，采用Holt-Winters 時間序列預測方法學習，并提取潛在特征的時域信息，以此較好地解決了鏈路預測問題.

基于矩陣分解的鏈路預測方法主要是對網絡的鄰接矩陣進行低秩分解，通過迭代分解矩陣，提取動態網絡的時變特征.然而在大規模動態網絡中，迭代矩陣分解會導致極高的時間復雜度，會增加系統的響應時間和影響用戶的使用體驗.

1.3 基于機器學習的鏈路預測方法

基于機器學習的預測方法是指利用機器學習算法從一定角度提取網絡中數據的特征，從而實現鏈路預測.

文獻[14]考慮到個體偏好可能是形成鏈路的主要原因，將效用分析概念引入到鏈路預測問題中，并關注了鏈路形成過程中潛在變量的演變過程.由此，將鏈路預測問題定義為一個帶有潛在變量的機器學習過程，并采用期望最大化算法來解決鏈路預測問題.文獻[15]應用圖卷積網絡（graph convolutional network,GCN）、長短期 記憶網 絡（long short-term memory,LSTM）和生成對抗網絡（generative adversarial network,GAN）提取加權動態網絡中鏈路變化的非線性特征，并利用GCN 獲取每個快照的局部特征，然后利用LSTM 來提取動態網絡的演化特征，以此提高了預測模型的準確性.文獻[16]針對單鏈鏈路預測指標普適性較差的問題，提出了一種基于密度峰值聚類的自適應鏈路預測方法.該方法采用不同的鏈路預測指標作為鏈路的屬性，并利用聚類分析將鏈路預測問題轉化為分類問題.文獻[17]將關系主題模型和貝葉斯深度學習框架相結合，構建了關系深度學習模型，然后推導出廣義變分推理算法來學習變量，并完成鏈路預測.文獻[18]將多節點鏈路預測問題轉化為模式分類問題，通過對網絡進行劃分獲得一系列網絡快照，并計算每個快照的狀態圖，然后構建基于卷積神經網絡（convolutional neural network,CNN）的預測模型，提取圖的演變特征，從而實現了多節點的鏈路預測.文獻[19]將動態網絡劃分為一系列時間序列快照，利用自動編碼器和LSTM 構建模型，以此實現鏈路預測.文獻[20]分析了動態異構網絡的特性，提出了時間感知多關系鏈路預測的特征集，然后構建并訓練了基于隨機深層森林的預測模型，并對特定類型的鏈路進行了預測.

基于機器學習的鏈路預測方法是通過大量數據訓練深度學習模型，再使用訓練完畢的模型對網絡完成鏈路預測.然而真實數據的復雜性以及動態網絡的稀疏性嚴重影響了模型的訓練效果，導致模型預測性能下降.

針對上述研究現狀，本文提出了一種用于移動社會網絡的鏈路預測模型（encoder-GRUs-decoder,EGRUs-D），能夠較好地解決真實數據高維度、非線性所造成的鏈路預測困難，同時還能緩解數據稀疏性導致模型訓練時可能產生局部最優的問題.由于采用了自動編碼器的結構，該模型可以幾乎無損地學習網絡表示，并根據所提取的信息重構網絡圖.經過編碼器模塊降維后的數據更容易被堆疊的門控循環單 元（gated recurrent unit,GRU）模塊學 習.本文在KONECT 的3 個真實數據集上進行了大量實驗.結果表明，相比于其他方法，E-GRUs-D 模型預測性能良好，且在訓練效率方面優勢明顯.本文主要貢獻有2 個方面：

1）提出了一種E-GRUs-D 深度學習模型來預測移動社會網絡中的鏈路，自動編碼器結構能夠以較少的損耗學習網絡表示，同時在輸入時降低數據維度以減少堆疊GRU 模塊的工作量，并在輸出時能夠根據提取的特征還原數據維度.GRUs 模塊能夠有效學習數據的時變特征，保證了預測結果的準確性.

2）E-GRUs-D 模型在保持預測準確率良好的基礎上，極大地縮短了訓練時間.通過改變不同隱藏層單元的數量，能夠適用不同規模的網絡，具有較好的可擴展性.

2 方法描述

2.1 問題定義

在固定時間間隔下生成的一系列快照圖可以用來表示一個移動社會網絡.

定義1.移動社會網絡.假設有一組圖序列（G1,G2,…,Gt），其中Gk＝（V，Ek）表示移動社會網絡的第k張快照圖.V表 示節點集 合，Ek?V×V表 示第k時刻快照中節點的鏈路情況.假設Ak表示圖Gk的鄰接矩陣，若節點vi和節點vj在時刻k產生鏈路，則矩陣Ak的元素ak;i,j＝1，否則ak;i,j＝0.

在靜態網絡中，鏈路預測主要根據已觀測到的鏈路分布來尋找實際存在的未知鏈路.而預測動態網絡時則需要利用網絡的歷史信息，尋找網絡演變的規律.由于鄰接矩陣能夠簡化網絡中節點鏈路情況的描述，所以本文模型的輸入和輸出將以鄰接矩陣的形式進行設置.雖然這些相鄰時刻的網絡圖聯系較為密切，也許僅僅通過上一時刻圖Gt-1也能預測下一時刻圖Gt中節點的鏈路狀況，但是這種預測方法存在一定的缺陷，因為圖Gt中包含的特征太少，并且隨著時間的推移，網絡結構會不斷發生改變，所以只使用一張圖預測時效果不佳，故本文使用一組長度為N的圖序列（Gt-N,Gt-(N-1),…,Gt-1）來預測下一時刻網絡圖Gt.

定義2.移動社會網絡的鏈路預測.定義一組長度為N的圖序列S，其中S＝（Gt-N,Gt-(N-1),…,Gt-1），本文使用E-GRUs-D 模型學習網絡的演變，使得輸入圖序列S后可獲得圖Gt.

移動社會網絡鏈路變化示例圖如圖2 所示.假設圖2（a）為時刻t＝1 的網絡鏈路情況，圖2（b）為時刻t＝2 的網絡 鏈路情 況.在下一時刻，邊E（1,4）和 邊E（5,3）消失，而邊E（4,5）和邊E（1,5）出現，在鄰接矩陣上則可體現為對應元素由0 變為1，或者由1 變為0.通過鄰接矩陣可以清晰地觀測到鏈接的出現或消失.本文主要通過節點的歷史信息來預測目標時刻可能出現的鏈路，如果將這一過程映射到鄰接矩陣上，即觀察矩陣中哪些元素的數值由0 變為1.

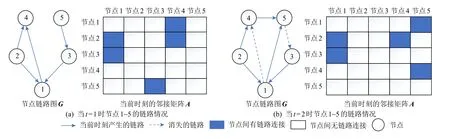
Fig.2 Example diagram of link changes in mobile social network圖2 移動社會網絡鏈路變化示例圖

2.2 E-GRUs-D 模型

本文提出了一種用于移動社會網絡鏈路預測的深度學習模型E-GRUs-D，該模型如圖3 所示.E-GRUs-D 由自動編碼器模塊和GRUs 模塊組成.GRUs 模塊中包含多個GRU 細胞，如圖4 所示，其中H0表示初始時刻的候選狀態數值，Ht-1為最后一個GRU 細胞的輸出，即最終提取到的時變特征.（Xt-N,Xt-(N-1),…,Xt-1）表示（Gt-N,Gt-(N-1),…,Gt-1）降維度處理后的輸入圖序列.

循環神經網絡（recurrent neural network,RNN）的變體有2 種：GRU 和LSTM，它們的數據輸入方式也與RNN 相似，通過這種依次輸入并記憶再輸入的循環方式，能夠較好地增強數據之間的聯系，提高模型在處理時間序列時的預測性能.此外，由于GRU 細胞結構的簡潔性，其訓練效率比LSTM 更勝一籌.

基于自動編碼器的特性，本文將編碼器部分和解碼器部分分別放置于模型的輸入端和輸出端，在自動編碼器模塊之間加入GRUs 模塊來提取數據的時變性.

1）自動編碼器結構.自動編碼器能夠以無監督學習的方式以較低損耗的代價學習網絡表示，其核心思想是實現函數y（x）=x的功能，即模型的輸入等于模型輸出.因此，將編碼器放在模型的輸入端來捕捉高階非線性的網絡結構，將解碼器放在模型的輸出端，使提取到的時變特征還原到先前的維度，并嵌入到網絡的鄰接矩陣中.由于初步輸出的矩陣中元素數值為0 的個數遠遠大于元素數值為1 的個數，這可能導致解碼器更傾向于忽略那些數值為1 的元素，即那些已經存在的鏈路，所以需要引導解碼器更注重于先前數值為1 的元素去構建矩陣.編碼器的執行過程表示為：

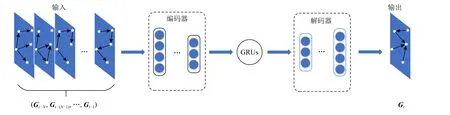
Fig.3 E-GRUs-D model structure圖3 E-GRUs-D 模型結構

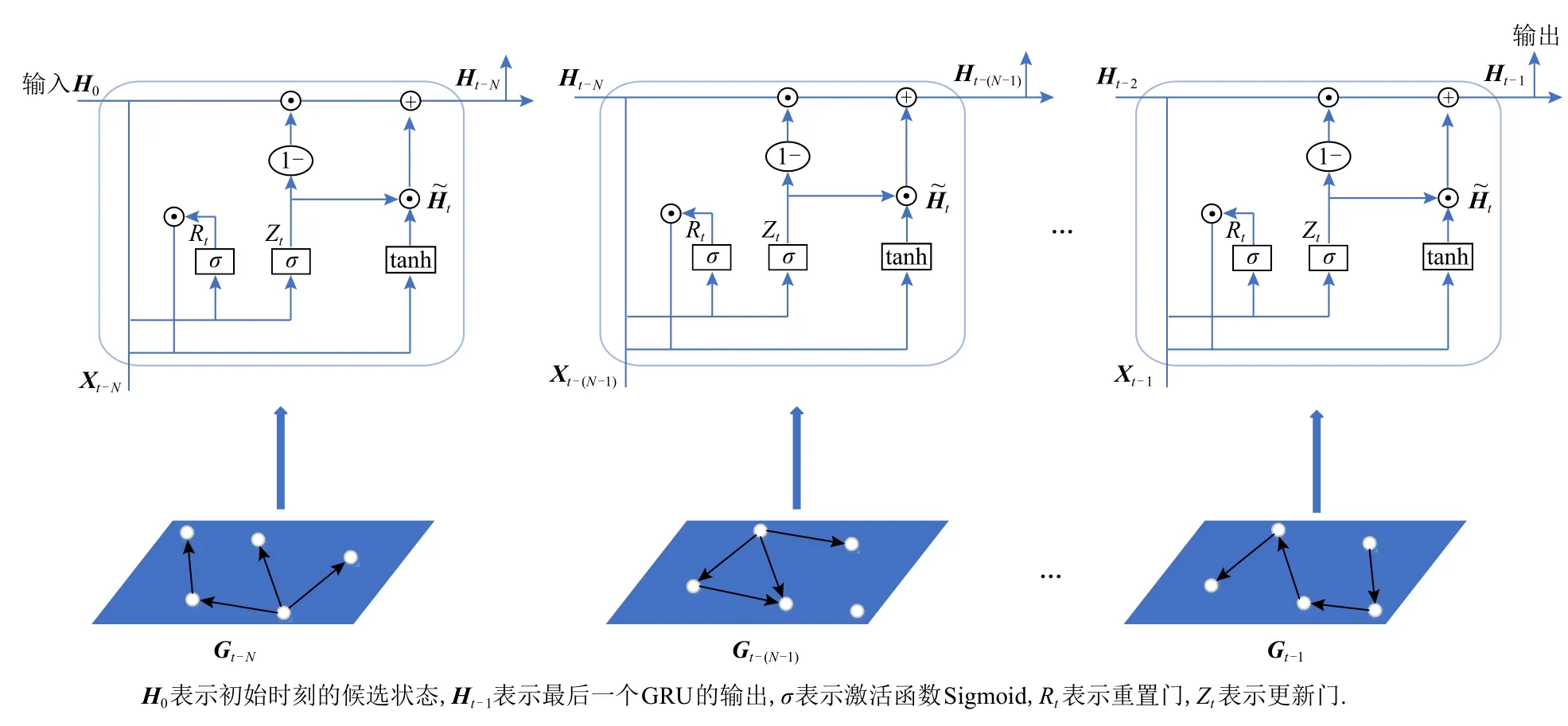
Fig.4 GRUs module details圖4 GRUs 模塊細節

式（1）中，si表示輸入序列S的第i張圖的鄰接矩陣.式（2）中，We;k和be;k表示第k層編碼器的權值矩陣和偏置矩陣，表示第k層編碼器輸入第i張圖產生的輸出.式（3）中，Ye;k表示第k層編碼器輸入整個序列時產生的輸出.對于編碼器層激活函數的選取，本文保存了自動編碼器結構的默認設置，仍選取ReLU作為其激活函數.

編碼器部分和解碼器部分互為鏡像結構，它接收GRUs 模塊學習而來的特征，重構先前的空間結構并將它們映射到鄰接矩陣內，該過程表示為：

式（4）中，U表示GRUs 結構的輸出，即提取到的特征.式（5）中，Wd;k和bd;k表示第k層解碼器的權值矩陣和偏置矩陣，Yd;k表示第k層解碼器的輸出.該結構仍和編碼器結構一樣，選取ReLU作為其激活函數.式（6）中 σ表示激活函數Sigmoid，這是為了在解碼器的最后一層實現歸一化處理.

2）GRUs 結構.雖然自動編碼器結構能夠處理高階非線性類型的數據，但并不能捕捉圖序列中的時間特征.GRU 作為RNN 的變體，能夠學習動態網絡中節點的歷史信息，其結構簡潔，又能在提取效率上優于LSTM.因此本文使用此結構作為該模型的隱藏層提取數據的時變特征.一個GRU 細胞由2 種門組成，分別是重置門和更新門.GRU 對于輸入值的處理程度主要依靠候選狀態Ht和隱藏候選狀態這2 個變量決定，隱藏候選狀態決定著候選狀態，而候選狀態影響著時刻tGRU 的輸出保留了多少歷史時刻的輸入.首先，數據輸入到GRU 中經過重置門，通過輸出重置值Rt來重置當前時刻的隱藏候選狀態，該過程定義為

其中，Xt表示時刻t的輸入；Rt表示時刻t的輸出；Ht-1表示時刻t-1 的候選狀態，當t=0 時一般取默認值或設置為0；Wr表示重置門的權值矩陣；[,]表示2 個向量相連操作；“· ”表示矩陣點乘，其運算結果為標量；σ表示重置門的激活函數Sigmoid.

在同一時刻，輸入數據流入更新門，更新門會更新當前的狀態信息，以決定對歷史信息的保留程度，該過程定義為

式（8）中，Zt表示時刻t更新門的輸出，Wz表示更新門的權值矩陣.然后，更新門根據重置值Rt和更新值Zt對隱藏候選狀態和候選狀態Ht進行操作，該過程定義為

最后GRU 根據候選狀態Ht輸出結果，該過程表示為

由式（7）～（11）可知，當Zt=1時，GRU 會完全摒棄過去的候選狀態即歷史信息；當Zt=0時，GRU 會完全復制當前時刻的上一時刻的候選狀態.重置門用于控制前一時刻有多少信息被寫入到當前的隱藏候選狀態中，重置門的值越小，則的值越小，即前一時刻的信息被寫入當前時刻的信息就越少.更新門用于控制前一時刻的狀態信息被帶入到當前時刻狀態中的程度，更新門的值越大，則式（10）對的側重就越強，即前一時刻的狀態信息被帶入的越多.通過這種模式，GRU 細胞能夠對歷史信息有選擇地保留.雖然單個GRU 層已經初步具備學習節點歷史信息的能力，然而效果并不是很理想，為了充分利用GRU 在時間處理方面的優秀能力，本文將根據輸入圖序列的長度N，將多個GRU 串聯起來，這種串聯堆疊的GRUs 模塊可以更好地處理具有時變特性的網絡，從而有效提高模型預測的準確率.

3）隱藏層節點數量的設置.隱藏層節點的數量與模型提取數據特征的能力密不可分，不同節點數量的隱藏層具有不同的提取能力.如果節點數量設置太少，則提取能力不足，容易增加模型重構數據時的誤差；反之，則會增加模型的復雜度，產生多余的資源開銷，并且容易出現過擬合問題.節點數量的設置主要由下列公式確定：

式（12）和式（13）中，Sn表示隱藏層節點的數量，m表示模型的輸入維度，n表示模型的輸出維度，考慮到數據集的大小和計算開銷，本文選擇式（13）來計算隱藏層節點的數量.

4）梯度算法的設置.梯度算法決定了模型的收斂速度.E-GRUs-D 模型使用的是Keras 庫中的Adadelta優化器，由于Adadelta 能夠根據漸變更新的移動窗口調整學習速率，所以相比于傳統的SGD 隨機梯度下降優化器，Adadelta 具有更強魯棒性，且在設定的模型訓練次數完畢之前，Adadelta 能夠保持對參數的學習，同時無需設置其初始學習率，從而避免了設置參數時的主觀性.

2.3 訓練過程

在線性回歸問題中，L2范數常常被用來測量2 個樣本的相似度.然而如果僅僅使用該范數作為本文模型的損失函數，并不能很好地解決矩陣稀疏性所造成的過擬合現象.為了處理這一問題，應當把反向傳播的重點放在現存的鏈路上而非不存在的鏈路上.本文采用了文獻[20]所提供的損失函數Ltotal，該函數由基礎損失函數L和L2范數組成：

其中，L2范數通常用來避免模型進入過擬合狀態；α為超參數，其取值范圍是0～1；基礎損失函數L表示預測值和標簽值的差值并求和.

基于理論出發，鄰接矩陣At的元素值取值為0或者1.然而實際生成的數值均為小數.為了獲得有效的鄰接矩陣元素值，首先對這些小數進行歸一化處理，即在輸出層放置1 個Sigmoid 函數.然后進行一層過濾，若矩陣元素at;i,j＞ 0.5，則令at;i,j=1，即近似表示節點i和節點j之間存在鏈路，反之，令at;i,j＝0，即表示不存在鏈路.

對于模型的收斂，本文主要根據損失函數數值變動的幅度進行判斷.如果在模型訓練100 輪之后，損失函數的數值不再顯著變化（保留小數點后3 位不再變化），則判定模型收斂.由于本文采用的數據集規模適中，且GRU 模塊參數較少，所以模型更容易達到收斂但同時易產生過擬合問題.

2.4 抗噪性分析

離群點作為數據集中的一種異常點，它的產生可能由于數據格式異常、數據內容異常和事件偶然性造成的異常.對于前2 種異常的發生，本文在數據集預處理時已經進行規避，但對于第3 種異常情況，比如首次見面的人之間偶然產生的短暫且不具備重復性的對話，為了保證數據集的真實性，本文未將其從數據集中排除.因此造成了不同數據集之間分布的優劣，導致各個數據集形成的網絡在周期性上具有一定的差異，而這種差異會對模型的訓練造成影響，從而導致預測結果的不同.

2.5 空間復雜度分析

1）LSTM 主要維護4 套參數，分別是輸入門參數、輸出門參數、遺忘門參數和候選狀態參數，每套參數都由輸入參數input_size、輸出參數output_size、偏移項參數bias以及隱藏層參數hidden_size共4 部分組成，則LSTM 參數總量Num為

由于任意時刻LSTM 的輸出y均為ht，并未產生額外的映射，所以

假設LSTM 的輸入維度為p×g，隱藏層的節點數為p，則最終LSTM 的空間復雜度為

2）GRU 主要維護3 套參數，分別是重置門參數、更新門參數和候選狀態參數，每套參數都有其輸入和輸出以及偏移項，由于GRU 和LSTM 均為RNN 的變體，所以GRU 的參數計數過程與LSTM 相同，則最終GRU 的空間復雜度為

LSTM 和GRU 作為RNN 的變體，均能夠捕捉數據的時間關聯性，并且能夠有效抑制梯度消失或爆炸，但是LSTM 的參數量約為RNN 的4 倍，而GRU的參數量只有RNN 的3 倍，所以在模型復雜度方面，GRU 更加簡潔，同時這也是GRU 模型在訓練時更不容易出現過擬合問題的原因.因此，在相同的數據集下GRU 的訓練效率相比于LSTM 大大提高.

3 實 驗

本文所提出的模型將基于KONECT 的3 個移動社會網絡數據集進行評估，并與其他3 種基準方法進行比較.

3.1 數據集

本文使用了3 個現實生活中的移動社會網絡數據集，這些數據集均涉及人與人之間的交互記錄.在這些網絡圖中，節點代表參與者，而邊則表示與他人之間的聯系.數據集的部分具體信息如表1 所示.

Table 1 Basic Information for the Three Datasets表1 3 種數據集的基本信息

1）HyperText[21].該數據 集記錄 了2009 年ACM超文本會議中出席人之間面對面會談的情況，該會議于2009 年6 月29 日在意大利都靈舉辦，為期3 天.在該網絡中，節點代表會議出席人，邊代表出席人之間至少存在20s 以上的對話，并且每條邊都標注了接觸發生的時間.

2）Infectious[21].該數據集記錄了2009 年在都柏林科學畫廊舉辦的《傳染：遠離》展覽會期間人們之間的交流情況.在該網絡中，節點代表了畫展的參觀者，邊表示參觀者之間產生了至少20 s 以上的接觸，并且記錄了發生時間.

3）Haggle[21].該數據集記錄了人們在一定區域攜帶無線智能設備生活，并與他人產生往來的情況.在該網絡中，節點和邊代表的含義與網絡HyperText 和網絡Infectious 相同，并且同樣記錄了接觸的發生時間.不同的是，在Haggle 網絡中，同一時刻可能產生多條邊.

在輸入數據之前，要先對數據集進行預處理.首先，對數據集按照時間戳大小進行排序，保證模型所獲取的歷史信息的連續性和正確性.然后，排除數據異常值，如空值或殘缺值.再次，按照固定時間間隔為每個數據集生成快照，即將整個數據集劃分為一系列網絡圖，由于數據集中記錄的相鄰時刻鏈路產生的時間差均為20 s，所以固定時間間隔設置為20 s.考慮到存在同一時刻可能產生多條鏈路的情況，將同一時刻產生的鏈路歸屬到同一個圖中.本文將抽象的圖轉化為具體的鄰接矩陣，每個鄰接矩陣的維度設置為各個數據集對應的參加人數，為了保證數據集的充足和數據之間的時間關聯性，每個樣本以滑動窗口的形式進行創建，滑動窗口的長度等同于輸入圖序列長度N，即每個樣本的格式均為（Gt-N,Gt-(N-1),…,Gt）.實驗中N=10，矩陣序列（Gt-10,Gt-9,…,Gt）作為一個樣本，在該樣本中，前10 個矩陣作為模型的輸入，最后1 個矩陣作為此次輸入的標簽.每個矩陣中，存儲著當前時間的節點信息，若人們之間存在交談，則相應的矩陣元素數值設置為1，否則設置為0.在極端條件下，即某一時刻沒有任何人產生交談記錄，則生成零矩陣.本文按照鏈路產生的時間順序，將前75%的數據集設置為訓練集，將后25%的數據集設置為測試集，同時遵循滑動窗口規則，盡可能多地創建樣本，最終從數據集中提取出320 張網絡快照圖，其中前240 張快照圖作為訓練集使用，后80 張快照圖作為測試集使用.

3.2 基準方法

為了驗證E-GRUs-D 模型的性能，本文使用了3種基準方法與該模型進行對比，包括靜態網絡的鏈路預測方法node2vec[22]、深度學習模型DDNE[23]和深度學習模型E-LSTM-D[19].

1）node2vec[22].node2vec 是一種綜合考量深度優先搜索鄰域和廣度優先搜索鄰域的圖嵌入（graph embedding）方法.該方法常用于靜態網絡，它將網絡中節點的鏈路情況進行降維.在低維空間中，如果1對節點對應的向量距離越短，則表明2 個節點的相似性就越高，即這對節點產生鏈路的可能性越高.

2）DDNE[23].該模型借鑒了自動編碼器結構，模型的核心部分是2 個GRU 層，其中一層作為編碼器使用，另一層作為解碼器使用，編碼器模塊負責學習數據的時間變化特性，解碼器模塊則負責將提取的特征嵌入到未來網絡結構中.

3）E-LSTM-D[19].該模型使用了自動編碼器和長短期記憶網絡結合的方式構造模型，編碼器負責簡化數據，解碼器負責還原數據維度.隱藏層為多個LSTM 串聯組成，用來提取數據特征.

基于數據集的規模和對比實驗，首先將隱藏層層數設置為2，然后根據式（13）設置隱藏層節點數量.輸入層編碼器節點數量取默認值128，由于輸出層的輸出形狀要求與最終輸出的鄰接矩陣形狀相同，所以解碼器層節點數量設置為各數據集中的總參與人數.參數的具體設置如表2 所示.

Table 2 Number of Hidden Layer Nodes Under Each Dataset表2 各數據集下隱藏層節點的數量

3.3 評價指標

1）混淆矩陣（confusion matrix）.該指標是一個標準混淆矩陣，如圖5 所示.

在混淆矩陣中，預測類別為1 的為正樣本（Positive），預測類別為0 的為負樣本（Negative）.真陽率TPR表示所有真實類別為1 的樣本中預測類別為1 的占比，偽陽率FPR表示所有真實類別為0 的樣本中預測類別為1 的占比.TPR和FPR分別定義為：

其中TP表示模型正確預測為正樣本的次數，FP表示模型錯誤預測為正樣本的次數，FN表示模型錯誤預測為負樣本的次數，TN表示正確預測為負樣本的次數.根據TPR和FPR則能繪制出接收者操作特征曲 線（receiver operating characteristic curve,ROC）.其中TPR作為縱坐標軸，FPR作為橫坐軸.

2）AUC指標.AUC通常用于衡量靜態網絡鏈路預測方法的準確性，其表示ROC 下的面積，表示模型正確預測為正樣本概率大于錯誤預測為正樣本概率的可能性.假設在數據中有M個正樣本和 ?個負樣本，則共有M×? 對樣本.若有M1次出現正樣本和負樣本預測概率相同，有M2次出現正樣本預測概率值大于負樣本預測概率值，則AUC定義為

AUC數值越大則表明模型的預測性能越好.特別地，當AUC=0.5 時表明對于不論真實類別是1 還是0 的樣本，模型預測為1 的概率是相等的.

3）錯誤率ER.ER一般是指模型錯誤預測的樣本數量占總樣本數量的比例，是一種通用的性能指標，定義為

其中，at;i,j表示時刻t標簽矩陣中第i行第j列的元素值，表示時刻t輸出矩陣中第i行第j列的元素值，Q代表總鏈路數，n代表輸出維度.

Fig.5 Confusion matrix圖5 混淆矩陣

3.4 實驗結果

本文設置N＝10 作為E-GRUs-D，DDNE，E-LSTM-D這3 種模型的輸入序列長度，由于node2vec 方法無法處理時間序列，故直接使用圖Gt-1去預測圖Gt，以此完成性能評估.

本文在評價指標AUC和ER的基礎上對E-GRUs-D 模型和其他3 種基準方法進行了比較，并選取其中性能最好的2 種方法對比它們的模型訓練時間，預測性能對比實驗結果分別如表3 和表4 所示，模型訓練時間對比實驗結果如圖6 所示.

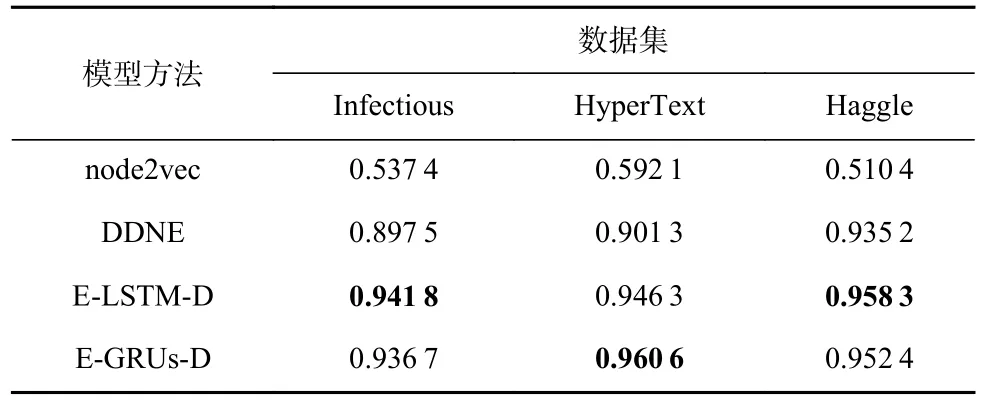
Table 3 AUC Evaluation Metric表3 AUC 評價指標

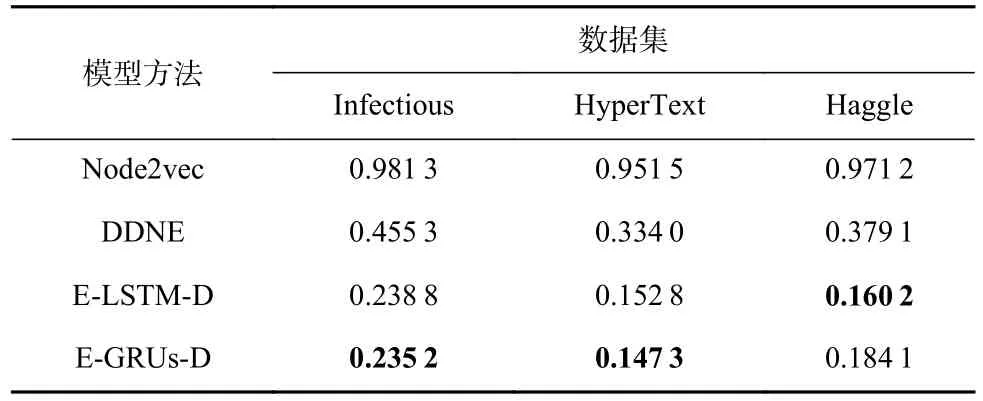
Table 4 ER Evaluation Metric表4 ER 評價指標

Fig.6 Comparison of training time圖6 訓練時間對比

在表3 和表4 中，node2vec 方法的鏈路預測準確率遠遠小于其他方法，這表明相比于用于動態網絡鏈路預測的方法，node2vec 并不能很好地學習移動社會網絡中節點的鏈路變化情況.總體而言，盡管ELSTM-D 模型的預測結果要略優于E-GRUs-D 模型，但圖6 表明，在3 種不同數據集下，E-GRUs-D 模型的訓練時間要遠短于E-LSTM-D 模型，體現了在相同數據規模下，E-GRUs-D 模型在縮短訓練時間上的優勢.

從實驗結果來看，E-GRUs-D 模型在不同的網絡規模、網絡密度中都能夠得到較為理想的預測效果，雖然其預測性能略低于E-LSTM-D 模型，但是訓練時間和計算效率得到顯著提高.此外，當在數據集規模較小的情況下，E-GRUs-D 的預測準確率超過了ELSTM-D 模型，該現象符合LSTM 和GRU 的特性：雖然GRU 和LSTM 內部均和“門控”這一概念密不可分，但是GRU 內部主要由2 個門進行運作，而LSTM內部則由3 個門進行運作，得益于GRU 內部構造的簡潔性，在數據集規模較小的情況下，GRU 的訓練效果會優于LSTM.

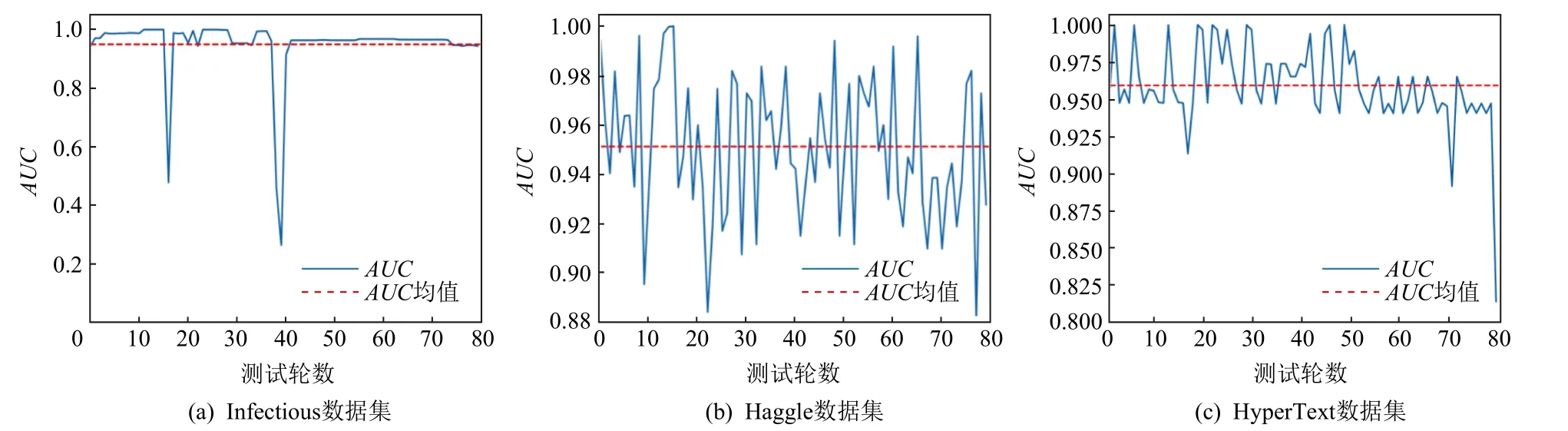
Fig.7 AUC values on different datasets圖7 不同數據集下AUC 值

Fig.8 ER values on different datasets圖8 不同數據集下ER 值

不同數據集下的實驗結果如圖7 和圖8 所示.其中，實線是相應數據集下模型在測試集中不同測試輪數的評價指標結果，虛線表示其結果的平均值.從這2 個圖可知，本文所提出的E-GRUs-D 模型具有穩定良好的預測效果，其中在Haggle 數據集下，預測的穩定性相對于Infectious 數據集和HyperText 數據集較差，這是由于Infectious 和HyperText 這2 種網絡的演變更具有周期性，更易于模型的學習，從而可以得到穩定性更強的預測結果.

模型預測結果波動較大是因為數據集中存在一些偏差點，比如首次見面的人之間偶然性的對話，由于在數據集中該節點對之間產生的數據較少，模型對于該信息無法進行充分的學習，故模型測試時在某段數據上易表現出較大的波動.

如果忽略掉個別離群點，如Infectious 數據集對應圖中的離群點，那么基于該數據集的預測結果在預測穩定性、指標平均值都較優于其他2 個數據集，這是因為在數據規模上，Infectious 數據集要大于其他2 種數據集，它能夠提供給模型更加充足的信息，使模型提取到足夠的歷史信息，更好地訓練得到網絡的時間變化特性.

3.5 參數設置實驗

E-GRUs-D 模型的性能主要受到模型結構和輸入圖序列長度N的影響，下面將展開相關實驗.

1）模型結構的影響.模型結構主要由隱藏層節點數量和隱藏層層數決定，借助于式（13），隱藏層節點數量可以確定，所以本文在相同節點數量的條件下觀察隱藏層層數對預測結果的影響.

圖9 和圖10 為隱藏層層數對模型性能影響的實驗結果.可知，在任何一種數據集下，當隱藏層層數設置為1 時，模型的學習能力不足，所以必須通過增加層數來提升模型的學習能力；當隱藏層層數設置為2 時預測效果最佳；當層數設置為3 時，由于提取了過多無用的信息，并且計算量隨著層數增多而急劇增加，預測效果反而下降.

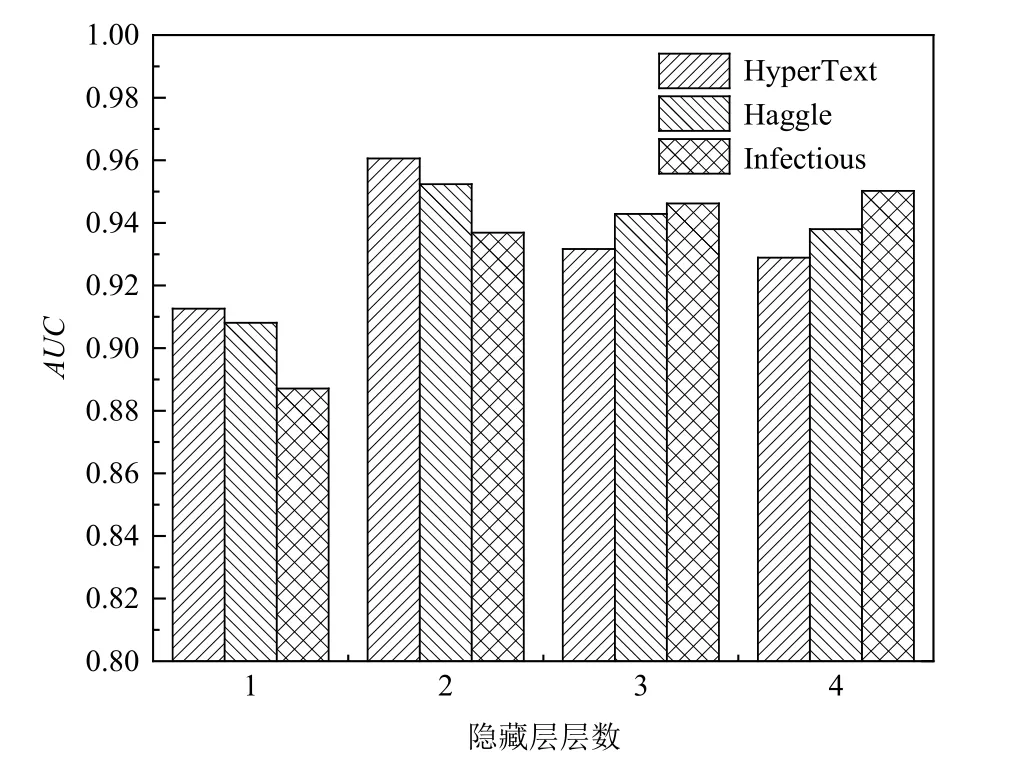
Fig.9 Influence of the number of hidden layers on AUC values圖9 隱藏層數對AUC 值的影響

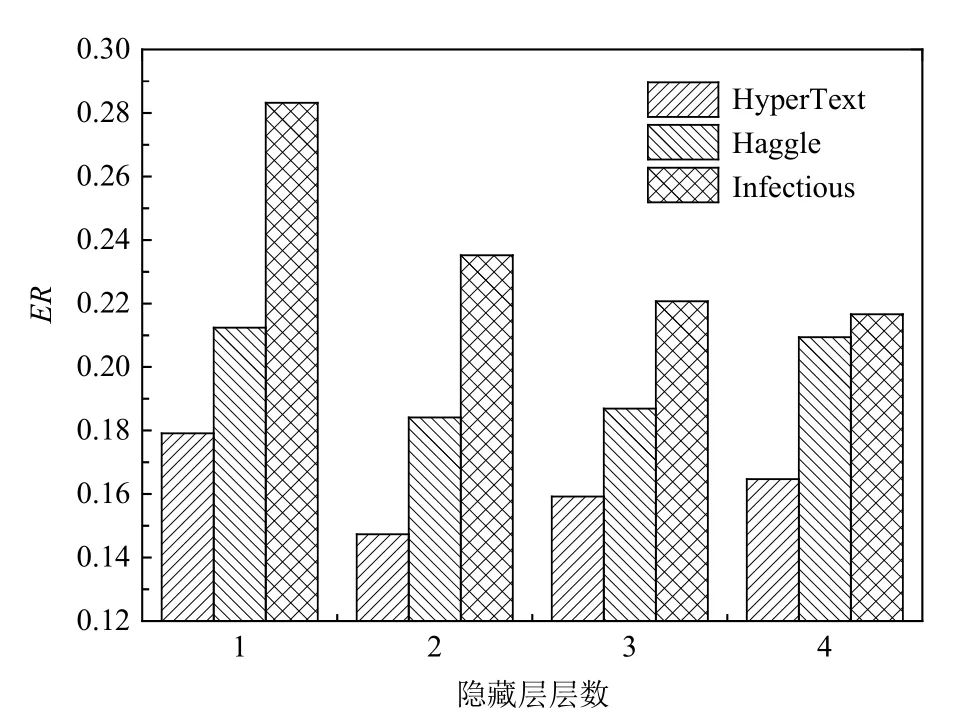
Fig.10 Influence of the number of hidden layers on ER values圖10 隱藏層數對ER 值的影響

2）輸入圖序列長度的影響.一般來說，輸入的圖序列越長，其中包含的歷史信息就越多，模型能更好地學習網絡的演變，預測準確率也越高.

然而，實驗結果表明如果輸入的圖序列過長，則其中可能會包含過多不相關的特征，導致資源浪費.因此，合適的輸入圖序列長度對于模型的預測性能也至關重要.本文在各數據集下測試了N從5 到15變化時對模型性能的影響，實驗結果如圖11 和圖12所示.對于規模較小的數據集HyperText 和數據集Haggle 而言，在N取值為11 之前，其預測性能隨著長度的遞增而不斷提升，而N取值超過11 之后，性能開始降低，這是因為當輸入序列過長，模型學習到過多冗余的歷史信息.由于Infectious 數據集規模較大，在整個過程中模型性能都隨著N的增加而增加，但在N取值為11 之后，模型的性能提升幅度減緩，需要注意的是，這種性能緩慢提升需要耗費巨大的模型訓練計算量.

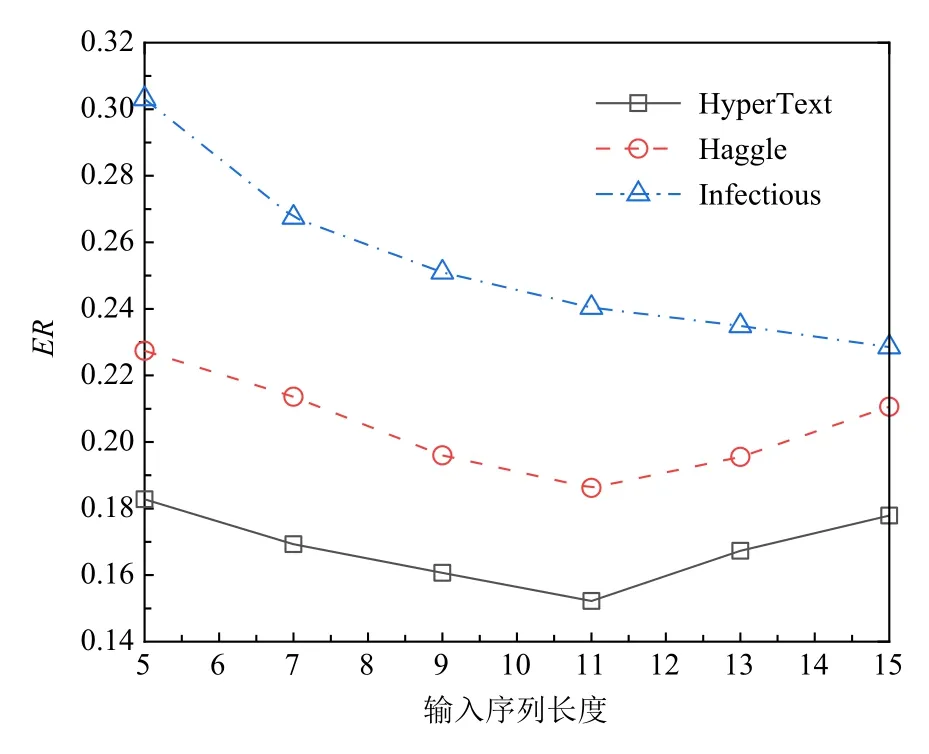
Fig.12 Influence of the input sequence length on ER values圖12 輸入序列長度對ER 值的影響

4 結論

本文提出了一種適用于移動社會網絡鏈路預測的E-GRUs-D 模型，該模型的Encoder-Decoder 模塊能夠學習高階非線性的網絡結構，從而降低了隱藏層的計算量，同時將提取的特征重構至先前的維度并映射到目標時刻網絡的鄰接矩陣中.GRUs 模塊的復數個GRU 串聯結構，首先能使模型提取數據的時變特征；其次，和只有1 層GRU 相比，學習能力更強，有助于提升模型預測性能；而且由于自身結構的簡潔性，該方法在縮短訓練時間方面要明顯優于現有方法；還能通過調整節點數量，適用不同規模的網絡，具有良好的可擴展性.大量的實驗表明，對于移動社會網絡的鏈路預測問題，該模型具有較為高效且準確的預測性能.

E-GRUs-D 模型和E-LSTM-D 模型在相同數據集下，模型性能差距較小，但是由于GRU 擁有相對于LSTM 較低的模型復雜度，所以在模型訓練效率方面更加優秀.然而，不論是LSTM 還是GRU，只是相對于RNN 而言，更加能夠抑制梯度消失或爆炸，且作為RNN 的變體，有著和RNN 結構同樣的弊端，即無法進行并行計算，所以在數據量不斷劇增以及模型體量不斷增大的未來，我們的研究將更加注重模型本身的優化，盡可能進一步抑制梯度消失和提高模型運算效率.

作者貢獻聲明：劉林峰提出指導性意見并修改論文；于子興提出算法思路和實驗方案，完成實驗并撰寫論文；祝賀負責收集實驗數據和完善實驗方案.