分布式多維大圖迭代計算性能優化方法

杜玉潔 王志剛 王 寧,2 劉芯亦 衣軍成 聶 婕 魏志強 谷 峪 于 戈

1（中國海洋大學計算機科學與技術學院 山東青島 266100）

2（密碼技術與信息安全教育部重點實驗室（山東大學）山東青島 266237）

3（青島市大數據中心 山東青島 266071）

4（東北大學計算機科學與工程學院 沈陽 110819）

作為計算機科學中一種重要的數據結構，圖可以表示現實世界中各種元素間復雜的關系，例如互聯網中的社交網絡、生物學中的蛋白質網絡等.隨著大數據時代的到來，圖數據的規模呈爆炸式增長，截至2021 年1 月，Facebook 的月活躍用戶已超過28 億[1]，而用戶之間復雜的社交關系導致邊的規模更為龐大，這需要分布式處理框架提供可擴展的存儲和計算能力[2].然而，圖數據的各種應用分析通常需要進行高頻迭代以逐步逼近最優解，而迭代過程中需要以消息的形式交換頂點之間的中間計算結果.由于頂點可能分布于不同的分布式任務，這會產生大量的通信開銷.

常見的圖應用分析既包括網頁排名計算Page-Rank 和單源最短路徑（single-source shortest path,SSSP）等簡單算法，又包括社團分類SC（semi-cluster）[2]和復雜的多源最短路徑計算（multi-source shortest path,MSSP）[3]等復雜算法.其一條消息的結構均包括目的頂點標識符以及消息值，但簡單算法的消息值僅需一個基本數據類型即可表達，即單維消息值，如以浮點型數據表示PageRank 的網頁排名分數或SSSP 的最短距離值；復雜算法則需要若干基本數據類型聯合表達，即多維消息值，如以浮點型數組來表示MSSP中若干源頂點的最短距離值，以整型數集合表示SC中一個聚類內包含的實體等.面對海量圖數據的迭代處理作業，多維算法顯然會急劇增加消息通信開銷，嚴重制約分布式計算的性能收益.

為提高計算和存儲的可擴展性，大量分布式圖計算平臺已經被開發出來并從通用性、易用性、健壯性和性能提升等各個方面進行了優化、完善.其中關于通信優化的技術主要包括圖劃分[2,4-6]以及給定劃分后的消息合并[2]與頂點備份機制[7].圖劃分作為一個NP 完全問題[8]，難以在降低通信開銷的解耦合和環節水桶效應的負載均衡方面實現綜合最優.因此，如何在給定劃分結果的前提下進行通信優化，顯得格外重要.

現有分布式圖計算系統中的消息管理框架主要分為早期Pregel[2]與GPS[7]等系統采用的主動推送機制（push）和PowerGraph[9]以及HGraph[10]等系統采用的新型按需拉取機制（pull）.已有的消息合并和頂點備份以及融合改進技術[11]均在push 框架下完成.然而由于消息的目的頂點分布的局部性差，push 框架從機制上無法保證應合并消息被完全合并，嚴重制約實際性能收益；反之，pull 框架極大改善了局部性，能夠保證應合并消息被完全合并，可最大化消息合并收益.本文分析發現，對于PageRank 類算法，pull框架下的消息合并與頂點備份，在理論上可產生相同的性能收益.然而，對于多維消息算法，如MSSP，即使對某個源頂點相關的單維度消息進行了完全合并，不同源頂點所構成的多維消息值依然較大；而對于SC 等算法，受計算邏輯正確性約束，僅能合并消息的目的頂點標識符而不可合并消息值.因此，需在pull 框架下實現頂點備份機制，在保留非備份頂點消息合并（或僅合并目的頂點標識符）收益的前提下，通過頂點備份進一步優化通信性能.

然而，現有頂點備份方法均在push 框架下開發完成，其備份頂點值的同步策略依然采用push 方式，如果直接遷移到pull 框架下，會導致同一個迭代步中同時存在push 與pull 這2 種消息管理體制，破壞原有pull 框架的系統完整性與優化設計，比如高效的容錯管理以及較低的內存資源消耗等特性.此外，備份機制雖然可帶來通信收益，但會導致邊數據在不同分布式任務之間進行遷移，影響原圖劃分結果的負載均衡，加重分布式環境下水桶效應導致的延遲開銷.因此如何選擇一個較好的備份控制閾值，對于獲取最優的綜合性能至關重要.此外，對于MSSP類支持合并的算法，遷移邊會破壞消息合并所依賴的圖結構，降低合并收益，如何在合并收益與備份收益之間進行均衡，是另外一個巨大挑戰.

圍繞多維消息算法的通信優化問題，本文針對平衡合并收益與備份收益的挑戰，在新型pull 框架[10]下設計了輕量級頂點備份機制，采用按需同步備份頂點值和優先級拉取消息等策略，使頂點備份與pull 框架完美兼容；設計代價收益模型以均衡通信收益與偏斜延遲的影響，可根據數據集相關的線下先驗知識和應用算法相關的線上實時信息，自動計算最優備份閾值，強化備份機制的實際性能收益并避免繁瑣的手工閾值測試與選擇操作；針對MSSP 類可合并多維算法，從合并收益與備份收益2 個角度分析多源點并發數目的取值，以確保備份機制的性能收益.大量真實數據集上的實驗結果表明，傳統push備份機制的內存開銷均大于較本文提出的輕量級備份框架，最高可達15 倍；對比現有非備份的pull 框架，本文框架可實現高達53%的性能收益；而代價分析模型則可有效選擇較優的備份閾值，實現與手動調整相近的性能收益.

1 相關工作

通信開銷一直是制約分布式圖處理性能提升的關鍵因素.本節總結了當前主要的相關工作并闡述本文技術與它們的區別.

1）圖劃分優化.高質量的圖劃分算法旨在解耦圖數據以減少子圖間的關聯關系，進而減少通信開銷，同時確保各任務的負載均衡以減少并行計算的水桶效應[12].然而，圖劃分問題屬于NP 完全問題[8].簡單的Hash[2]和Range[10]劃分可分別保證頂點和邊數據的均衡分配，雖然頂點或邊的切割會引起較高的通信開銷，但由于劃分速度快，已成為當前主流的劃分機制.此外，多級層次劃分算法如Metis[6]，PaToH[13]，KaHIP[14]等通過反復迭代調整數據分配位置，可顯著降低通信開銷，但執行效率過低.而流式劃分[5]嘗試均衡通信優化質量和劃分執行效率.本文的通信優化機制是針對給定劃分后的子圖進行2 次優化，因此兼容上述圖劃分技術.

2）消息傳遞優化.除圖劃分外，在迭代計算過程中也存在很多通信優化技術.谷歌的Pregel 系統[2]首先針對多對1 結構提出消息合并策略.Pregel 的開源實現GPS 系統[7]則提出LALP 策略，對高出度頂點進行邊遷移并備份源頂點；而以此為基礎，進一步的工作探討了如何在備份遷移過程中保證負載均衡[14-16].Pregel+[11]在消息合并基礎上融合LALP，并增加邊遷移（即源頂點備份）閾值的討論，以在合并與備份之間進行均衡.然而，上述系統均采用push 機制，這是由于目的頂點分布的局部性差，消息合并收益較低.不 同于push 框 架，PowerGraph[9]，CGraph[17]，HDRF[18]等框架在數據加載過程采用頂點分割策略，并設計了對應的GAS（gather-apply-scatter）迭代計算框架，可同時支持圖算法和機器學習算法，其中Gather 即pull機制的核心部件.然而，頂點切分引入大量內存開銷[19]，且GAS 計算頻繁觸發頂點之間的同步操作，開銷較大.為此，PowerLyra[20]，GrapH[21]，L-PowerGraph[22]，LightGraph[23]等分別從頂點切分策略與頂點間消息傳遞方面進行優化.最近提出的HGraph 系統[10]則給出了以塊為單位進行消息拉取的新型pull 框架，顯著改善了消息目的頂點分布的局部性，可實現完全徹底的消息合并，在不進行頂點切分的前提下，針對值合并類算法，其性能顯著優于傳統pull 框架且在內存消耗與容錯控制方面均有較大優勢.然而，多維算法由于其消息值本身的字節規模較大，使得HGraph 在徹底合并消息（值或目的頂點ID）后，通信代價仍然較高，亟需通過頂點備份進一步降低相關開銷.

近年來，基于特定硬件架構的圖計算優化問題已經成為另一個研究熱點[19,24]，但本文關注通用架構下的通信優化，不對硬件條件進行特定假設.

2 問題定義

本節首先闡述分布式圖迭代計算的一般處理方式；然后根據消息數據的維度以及合并屬性對圖迭代算法進行分類，并著重介紹近些年提出的具有重要實用價值的多維消息類算法；最后基于推送（push）和拉取（pull）這2種主流分布式消息管理框架，分析合并與備份對不同類型圖算法的優化效果.

2.1 分布式圖迭代計算

給定輸入的有向圖G=〈V,E〉,其中V為|V|個頂點的集合而E為|E|條邊的集合.E中每條有向邊e=〈vi,vj〉連接源頂點vi和目的頂點vj，其中vi是vj的入度鄰居/頂點，而vj是vi的出度鄰居/頂點.圖以鄰接表形式存儲，每條鄰接表包含頂點vi和所有以vi為源頂點的出邊的目的頂點.

分布式圖迭代計算系統在啟動迭代計算之前，首先將G從初始存儲位置（如分布式文件存儲系統HDFS）并行加載到P個不同的分布式計算任務Ti上，每個任務負責處理一部分數據，即子圖Gi=〈Vi,Ei〉,該過程即圖劃分；隨后各任務Ti對本地子圖Gi中的圖數據進行迭代計算，計算過程中消息的生成、發送和接收處理都是按照出邊進行的，相應頂點循環執行更新操作，每次循環即一個迭代步，迭代步之間通過全局同步路障來協調各個任務的處理進度.第k個迭代步的具體操作包括：根據第k-1 步接收的消息更新頂點值，將更新后的頂點值以消息的形式沿著出邊發送給目的頂點，以便在第k+1 步執行更新操作.如果頂點vi參加第k步迭代的更新計算，則稱vi在該迭代步是激活的，編程人員可根據需要設置激活標記，以避免非激活頂點的無效計算.當所有頂點均處于非激活狀態且系統中沒有新的消息生成時，算法收斂，迭代計算結束.

2.2 多維消息類圖迭代算法

依據分布式圖算法在迭代計算過程中傳遞消息的不同維度特征和合并屬性，可對分布式圖算法進行分類.具體分類標準包括：1）一條消息數據的消息值可以由單個基本數據類型獨自表達或多個基本數據類型聯合表達，即單維與多維；2）發往同一個目的頂點的不同消息值是否允許被合并為一個值，即值合并和連接.表1 展示了常見分布式圖算法的分類結果.下面以SSSP、標簽廣播算法（label propagation algorithm，LPA）、MSSP 和SC 為例，分別按照2 種分類標準對不同類型算法的特征進行闡述.

Table 1 Graph Algorithm Classification表1 圖算法分類

SSSP 算法的目標是發現給定源頂點到圖中其他所有頂點之間的最短距離.迭代初始階段，源頂點將頂點值（即距離值）初始化為0 并根據出邊的距離權重生成消息值發送給出度頂點，而其余所有頂點均將頂點值設置為無窮大.隨后，每步迭代過程中，收到上一步消息的頂點被激活并從入度鄰居的消息值和自身頂點值中選擇最小的值進行值更新，而如果頂點值發生了更新，則沿出邊生成新消息并發送給出度鄰居.每條消息msg=〈ID,msgValue〉，其結構僅包括一個int 型的目的頂點ID和double 型距離值msgValue,屬單維消息.此外，算法邏輯僅關心最短距離值，所以如果沿2 條或多條目的頂點相同的出邊如e13=〈v1,v3〉和e23=〈v2,v3〉,分別生成具有不同消息值的消息如msg13=〈3,0.1〉和msg23=〈3,0.5〉,則可合并為一條消息msg=〈3,min{0.1,0.5}=0.1〉以節省通信開銷.

LPA 是一種快速社團發現算法，其將每個頂點賦值一個社團標簽并初始化為頂點ID,隨后迭代更新標簽值為其入度鄰居標簽值中出現次數最多者.由于頂點更新依賴所有入度鄰居的標簽值分布，所以每步迭代中每個頂點均參與更新且沿出邊向所有出度鄰居廣播自己的標簽值，即全激活.與SSSP 相比，其消息結構相同，即目的頂點ID和int 型的標簽值，屬于單維消息；但不同之處是，由于需要根據標簽頻數分布進行更新，所有消息值不可合并，僅可連接，即如有msg13=〈3,2〉和msg23=〈3,2〉，僅可連接消息值為msg=〈3,[2,2]〉以合并（共享）目的頂點ID進而節省通信開銷.

MSSP 是SSSP 的一種常見多源點擴展.高級圖挖掘與分析算法通常需要衡量圖中所有頂點對之間的最短距離，而通過串行提交不同源頂點的SSSP 作業，會造成圖的反復遍歷，效率低下.一種高效的解決方案是根據集群的計算與存儲能力，在一個圖遍歷作業內并發計算多個源頂點的最短距離分布，即MSSP.假設并發源頂點個數為m，則此時每個頂點值由一個double 型數據擴展為長度為m的double 數組；對應地，消息值也擴展為double 數組.例如，當m=3時，可有msg13=〈3,[0.1,0.4,0.2]〉和msg23=〈3,[0.5,0.3,0.1]〉,此時雖然對應源頂點的消息值可合并，但合并后的消息值仍是一個長度為3 的數組，即msg=〈3,[0.1,0.3,0.1]〉,故屬于可合并、多維消息類算法.其他單源點遍歷算法如PPR 和BFS 均有類似的多源擴展.

SC 是谷歌開源圖處理系統Pregel 中內置的一種半聚類算法，即允許一個頂點記錄自己所屬的多個聚類并打分排序.迭代初始，每個頂點將自身初始化為一個聚類并發送給出度鄰居.在每個迭代步，所有頂點均激活，根據入度鄰居所屬的聚類分布更新自己所屬聚類，并繼續廣播.算法傳播的消息是描述頂點所在的聚類（即頂點集合），需要多個基本數據類型進行聯合表達，屬于多維消息結構；且由于需要聚類分布信息，故消息值不可合并.延續上例，可有消息msg13=〈3,（1）|0.6,（2,5）|0.3〉和msg23=〈3,（2,5）|0.3〉,即頂點v1可歸屬于包含頂點v1的聚類（1）和包含頂點v2與v5的聚類（2,5）,分數分別為0.6 和0.3,而v2則以0.3 的分數歸屬于聚類（2,5）.與LPA 類似，2 條消息因對應的目的頂點相同故可以合并發送，但消息值僅可連接，即以msg=〈3,[（1）|0.6,（2,5）|0.3,（2,5）|0.3]〉的形式進行發送.

綜上，對于單維值可合并類算法，如果可以保證應合并的消息被全部合并，可極大緩解通信壓力；對單維值連接類算法，由于消息值不可合并，每個迭代步中總的消息值規模最多可達到出邊的數量級，即|E|，但由于每個消息值的字節數較少，故通信壓力仍可以接受；反之，對于多維消息類算法，其單條消息值的規模取決于聯合表達所用的基本數據類型的數目，即維度，如MSSP 算法中的并發源頂點數目和SC 算法中描述聚類特征的基本數據類型集合規模.在相同的輸入圖規模下，多維算法顯然會產生較大的通信壓力.而當消息值不可合并時，通信代價更會急劇增大.而根據已有測試結果，在分布式圖算法處理過程中，即使對于單維消息類算法，任務間通信引入的時間開銷約占總執行時間的50%以上[3].因此亟需針對多維消息圖迭代算法設計通信優化技術，以提升分布式計算效益.

2.3 消息合并與源頂點備份收益分析

分布式通信問題可以通過提升圖劃分質量加以改善，即在保證負載均衡的前提下盡量減少子圖之間的邊耦合依賴程度.然而，圖劃分是一個傳統的NP 完全問題[8]，難以在合理時間內獲得高質量劃分結果.因此，對已有劃分后的子圖進行后續通信優化就顯得尤為重要.目前的優化方法主要分為2 類：消息合并和頂點備份.下面結合push 和pull 這2 種消息傳輸方式分析2 種優化方法產生的效益，以突出本文研究的必要性.

2.3.1 push 與pull 消息傳輸方式對比

迭代過程中消息的生成與傳送方式可分為兩大類設計，分別為push 和pull.在迭代步k，push 在頂點更新時直接遍歷所有出邊并主動推送消息給所有目的頂點；而pull 僅完成頂點更新、不發送消息.在迭代步k+1，push 可確保目的頂點所需消息均已接收并儲備在本地，可直接使用；而pull 需要根據邊的依賴關系從對應源頂點處按需拉取消息數據.2 種消息管理框架各有優缺點，push 在一個迭代步中，僅需遍歷一次頂點即可完成頂點值更新和新消息生成，但由于頂點之間邊關系的自由分布，一個頂點的出邊所指向的目的頂點的分布具有較差的局部性，即主動推送的消息數據所指向的目的頂點的局部性差，且該部分消息直到下一個迭代步才被使用，因此需要在發送端和接收端設置大量消息管理緩存，需較多的內存資源；pull 由于消息按需生成且消息均指向欲更新頂點值的目的頂點，故局部性良好，且接收的消息可直接被目的頂點處理，無需緩存，極大節省了內存資源，但不同目的頂點的更新會導致其共享的源頂點被隨機掃描讀取多次.

2.3.2 消息合并

當某個任務上的多個源頂點均需要向同一個目的頂點發送消息時（多對1 結構），如果消息值可合并，顯然可以在消息發送之前進行合并（如2.2 節的SSSP 算法），以減少通信開銷.然而，在push 方式下，考慮到消息的目的頂點分布的局部性較差而發送端緩存又是有限的，因此能夠在緩存中參與合并的消息比例較少，即無法保證徹底的消息合并，導致通信收益降低，甚至難以抵消合并所引入的管理開銷.如圖1（a）所示，假設發送端緩存容量為2 條消息，可保證頂點v1與v2發往目的頂點d1與d2的消息被合并；但當v2繼續往d3發送消息時，由于緩存已滿，需將發往d1與d2的消息清空；最后v3往d2發送消息，但因緩存清空，該消息無法與v1與v2生成的消息合并，即應合并消息無法保證被徹底、完全地合并.相反地，在pull 方式下[5]，如圖1（b）所示，目的頂點按照2 為單位進行分塊，然后以塊為單位拉取所需消息.第1個塊中，消息均發往d1與d2，局部性優異，在緩存為2 的前提下，可被完全合并；之后第2 個塊啟動拉取操作.此外，這種按塊拉取的方式，可保證同一個塊內的目的頂點僅掃描1 次對應的源頂點，降低源頂點的隨機讀取次數.需要注意的是：這里的消息合并是泛化概念，即對于2.2 節中值合并類算法，可實現目的頂點ID與消息值合并；而對值連接類算法，僅可實現目的頂點ID的合并，其通信收益仍在，但效果減弱.

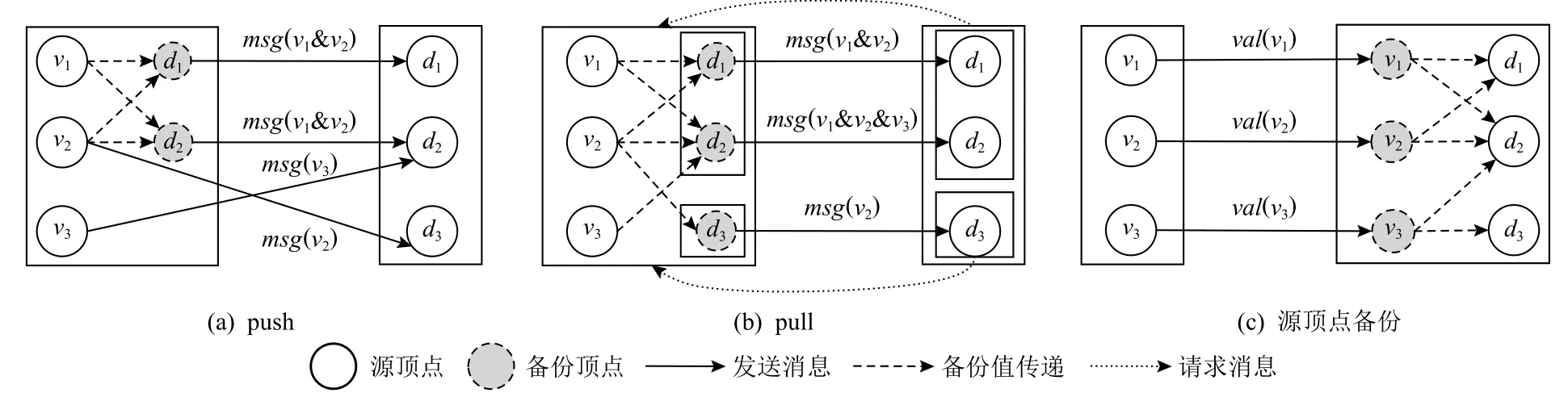
Fig.1 Illustration of message combination and vertex replication圖1 消息合并與頂點備份圖示

2.3.3 頂點備份

當某個頂點的出度較高以至于其在若干任務上均有大量的目的頂點（1 對多結構），可以將出邊遷移至目的頂點所在任務并對源頂點進行備份，從而將遷移邊所對應的網絡消息轉換為目的頂點所在任務的本地消息，同時增加了同步備份頂點值的網絡開銷.如圖1（c）所示，源頂點備份主要在傳統的push 框架下實現，如GPS[7]和Pregel+[11].當頂點更新后，同步備份頂點的值，而備份頂點收到同步值之后立即沿遷移邊生成本地消息.同步值與本地消息均采用push 方式管理.考慮到遷移邊的消息不再由源頂點所在任務生成，這會影響消息合并的機率.因此，對于消息合并類算法，Pregel+[11]設計了合并優先的備份機制，即只有當目的頂點的入度為1 時，其對應的源頂點才可能被備份（此時無其他源頂點指向該目的頂點，故不會損失合并收益），以兼顧合并與備份的收益.Pregel+[11]在非完全合并的push 框架下取得了較好的通信壓縮效果；但在新型pull 框架下，由于徹底合并已經極大壓縮了通信規模，根據我們的實測結果，如表2 所示，雖然滿足備份約束的頂點比例較高，但備份僅帶來1%～7%的微弱壓縮效果，而實際性能收益可以忽略.表2 所示的4 個真實圖數據集，包括互聯網領域的Web 圖數據集Uk2014tpd（UK）、Wikipedia（Wiki）和Eu2015host（EU），以及社交網絡領域的常用圖數據集LiveJournal（LiveJ）.

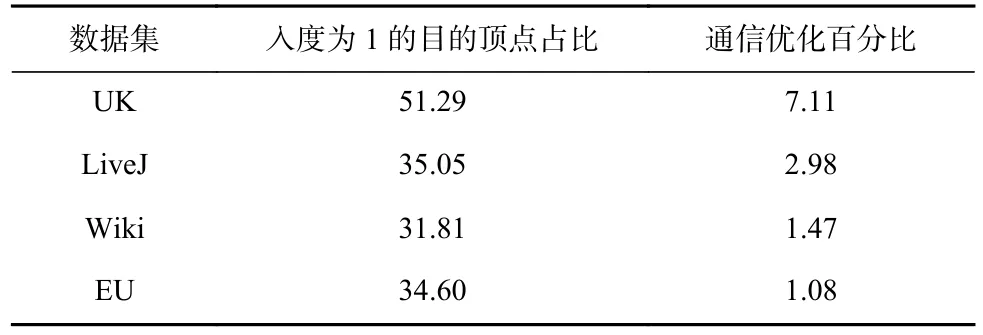
Table 2 Replicate Effect of Pregel+Under Thorough Combination表2 Pregel+在徹底合并下的備份效果 %

2.3.4 分析

對比消息合并和頂點備份機制可發現，對于合并類消息算法如SSSP,在以塊為中心的pull 框架下，其完全徹底合并消息的特點特別適合多對1 結構，合并后僅需發送一條消息.本質上，可以看作目的頂點在源頂點所在任務上的備份過程（如圖1（b）所示），最終的網絡通信代價取決于目的頂點的備份規模；另一方面，現有頂點備份適用于1 對多結構，僅有備份頂點的同步會引入網絡開銷，通信代價取決于源頂點備份規模（如圖1（c）所示）.因此，無論是對目的頂點還是對源頂點進行備份，備份后的通信規模都是由備份頂點的數量決定的.注意到PowerGraph[9]提供了關于求解頂點v在P個任務上備份頂點數的期望公式：其中d為頂點v的出度或入度，V是頂點集，|V|是頂點集中頂點個數，|V|與冪律偏斜指數 α和Zipf 分布的歸一化常數直接相關.其中，消息合并關心的目的頂點備份規模依賴入度偏斜，而源頂點備份規模則依賴出度偏斜.圖2 分析了本文所用真實數據集的出入度偏斜指數，可以看出兩者近似相等.因此，不同于傳統push 框架下的非完全合并，對于值合并類算法，pull 框架下的消息完全合可帶來與源頂點備份相近的通信收益；即使對于值連接類算法，pull 框架的優異合并效果依然可以在目的頂點合并方面帶來性能收益.

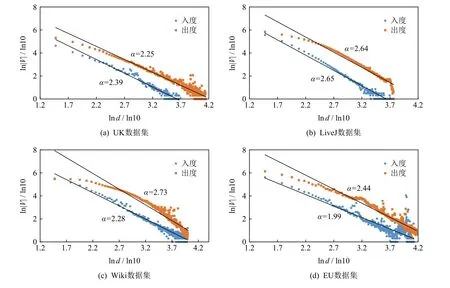
Fig.2 The skewness of the in/out degree distribution for different datasets圖2 各數據集的出/入度偏斜指數

特別地，對于MSSP 類圖遍歷算法，頂點值是逐步收斂的.在第k步迭代中，同一目的頂點所對應的多個源頂點中可能有頂點值已經達到收斂而停止更新，該部分頂點自然不會生成新消息.這種算法邏輯層面的部分收斂現象顯然會減少參與合并的消息規模，削弱多對1 結構產生的合并收益.相反地，頂點備份依賴1 對多結構.對于某個頂點而言，只要其尚未收斂，則需要繼續沿出邊廣播消息，頂點備份可繼續正常工作，不受頂點收斂的影響.這會在兩者之間產生通信收益差，且差值與消息值維度成正比，即MSSP類算法并發源頂點個數越多，2 種機制的通信收益差距越大.基于上述分析以及 pull 方法極低的內存消耗特別適合大規模圖數據處理，本文因此致力于在以塊為中心的pull 框架下，針對多維消息算法，通過源頂點備份機制進一步優化消息值的傳輸開銷.

考慮到源頂點備份會破壞原有圖劃分的均衡負載分布，且現有源頂點備份機制均在push 框架下設計，難以兼容新型pull 框架，因此需要重新設計備份機制并仔細分析備份閾值，以實現功能性和性能優化方面的統一.

3 輕量級頂點備份框架

由于大部分算法的基本工作流程是頂點更新與邊消息傳遞，而圖中邊的規模遠大于頂點規模，故工作負載與邊密切相關.因此，本文假設采用簡單快速的Range 劃分以保證劃分后各任務間的出邊數目均衡，然后通過對消息傳遞模型的改進降低網絡通信量，以實現圖處理性能的整體提升.然而，已有消息傳遞模型的改進主要是基于非完全合并的push 環境下進行的.為實現通信開銷的進一步壓縮，本文在完全合并的pull 環境下，即HGraph[10]系統上設計新的輕量級頂點備份機制，以改善多維消息算法的消息值傳輸效率.

輕量級頂點備份的核心是，在pull 系統下，備份點的相關操作也采用pull 方式實現；通過只使用一種pull 管理方式，避免了傳統push 頂點備份機制在pull方式下內存開銷大與容錯負載重的問題，程序設計簡潔、易維護.本節首先總結push 備份在pull 框架下的缺點，然后介紹輕量級備份的按需同步和優先級消息拉取技術，最后對比本文備份框架與PowerLyra的混合備份技術，突出本文備份的輕量級特點.

3.1 push 頂點備份與pull 消息管理框架的兼容性

根據2.3 節中對消息合并與頂點備份的收益分析可知，在完全合并的pull 框架下，兩者對值合并類算法的通信壓縮效果相近.但針對多維算法，在保證完全合并（目的頂點ID合并、消息值合并）的前提下，可針對部分高出度頂點進行邊遷移與源頂點備份，以進一步優化通信開銷.然而，目前源頂點備份對通信的改進都是在push 框架下實現的，備份頂點的同步以及遷移邊的消息生成方式，均采用push 主動推送方式，如果直接在pull 框架下實現，會導致每個迭代步內同時存在非備份頂點的pull 操作以及備份頂點的push 操作，帶來2 個缺點：

1）容錯管理復雜且效率低.容錯控制對圖迭代計算至關重要，可在部分任務發生故障時避免其他任務回滾、重新計算.目前的容錯機制主要采用檢查點回滾的方式進行故障恢復.為避免非故障任務的重新計算，需要不斷記錄每個任務的消息輸出，以便故障任務在重新計算時使用.大量的消息記錄，尤其是多維算法的大消息值特性，會嚴重影響正常迭代的計算效率.在push 方式下，由于消息是主動生成并發送出去，無法對此進行優化；而pull 方式允許消息按需生成，故可按需生成故障任務恢復過程中所需的消息，不必主動記錄.當故障節點需要入度鄰居的消息來更新頂點值時，僅需沿入邊向入度鄰居發送拉取請求，而非故障任務上的頂點只需記錄對應迭代步的頂點值以響應消息請求即可.由于頂點的規模遠低于消息規模，記錄頂點值對正常迭代計算的影響很小.然而，一旦pull 與push 混合執行，則仍需要對push 方式下的頂點同步值以及根據遷移邊生成的消息進行記錄，既增加了容錯管理的復雜性，也增大了容錯開銷.

2）多緩存高內存消耗.使用push 方式進行消息發送時，需要在發送端針對每一個分布式任務設置一個雙緩存結構，以便其中一個緩存溢出、進行消息發送時，另一個緩存可繼續接收消息、不阻塞頂點的計算更新；在接收端，由于消息對應的目的頂點的局部性差且無法預知其到達時間，需要根據目的頂點的分塊信息、消息源頂點所在的任務等設置多個緩存區，以避免針對同一個目的頂點的消息進行整理時導致頻繁的加鎖開銷.在多維消息類算法中，由于頂點值以及據此生成的消息值的規模巨大，發送端與接收端的多緩存設置給內存造成巨大壓力.而在pull 系統中，消息按需生成且生成之后被立即消耗，因此根據需要更新的目的頂點的規模預估消息規模設置緩存即可，避免了繁雜的多緩存結構，節省了內存開銷.同理，當pull 與push 混合時，為正確、高效運行push 機制，需要配備多個緩存結構，增大了內存開銷.因此，需要設計與pull 機制相兼容的頂點備份框架，在實現輕量級程序框架設計的同時，可以實現容錯和內存管理的簡潔與高效.

3.2 基于按需同步的備份更新策略

鑒于push 備份與pull 框架的沖突點是由備份點的同步方式以及遷移邊的消息生成方式所導致的，因此需要將這2 種方式改為pull 方式，以實現系統兼容.本節重點介紹基于按需同步的拉取式頂點備份機制.

3.2.1 按需同步框架設計

執行頂點備份后，每個迭代步中頂點值計算更新所需的消息來源于2 個部分：1）所有任務上非備份頂點發送的非備份消息值；2）備份到本地的頂點根據遷移出邊發送的本地備份消息值.當目的頂點塊欲執行更新操作時，針對非備份消息值，直接以塊為單位向所有任務發送拉取請求，而各任務接收請求后，直接掃描本任務內指向該請求塊內所有目的頂點的出邊，生成所需消息并在發送端執行徹底合并后發送給請求端（即目的頂點塊所在的任務），該過程可由現有pull 機制直接完成；而針對本地備份消息值，在按需同步策略下，某個頂點值被更新后，不會主動推送消息以同步其備份頂點值，因此應先同步其備份值，然后生成本地備份消息.具體地，在同步備份頂點值時，仍然以目的頂點塊為單位向所有任務廣播同步請求，而各任務收到請求后，檢索本地頂點是否有指向該請求塊內目的頂點的遷移出邊（即是否有備份），如是，則響應同步請求，將頂點值發送到請求端，然后根據同步后的備份頂點值生成本地備份消息.進一步地，為實現按需生成本地備份消息的目標，需將備份的源頂點和遷移的出邊以鄰接表的形式分塊存儲，即每個遷移過來的鄰接表按照目的頂點所在的塊對遷移邊進行分割存儲.如是，當目的頂點所在的塊欲執行更新操作而拉取消息時，僅需讀取每個遷移鄰接表中對應該塊的部分出邊即可生成所需消息，從而避免push 方式下的多種緩存設置，降低內存消耗.

3.2.2 2 階段同步響應優化

在同步響應過程中，各任務的檢索操作需要遍歷所有出邊，時間復雜度較高.此外，某個源頂點的出邊可能指向任務Ti上不同塊內的目的頂點.當任務Ti上不同塊內的目的頂點發送同步請求時，該源頂點所在的任務需進行多次檢索以及響應操作，造成備份頂點值的冗余同步，浪費計算和網絡資源.為提高同步效率，本文設計了基于字典的2 階段同步響應機制.具體地，每個任務在內存中維護同步響應字典，即如果某個頂點在某個任務上存在備份，則在字典中添加該條記錄，且標記該備份值在當前迭代步是否已經被同步.根據2 階段同步響應機制，當某個目的頂點塊欲向任務Ti發送同步請求時，其首先查驗本地是否存在來自于Ti的遷移邊，如果沒有，顯然無備份頂點，無需發送請求；如存在，則正常發送請求.任務Ti收到請求后，首先查驗響應字典，如果指向請求端所在任務存在備份點且所有備份點均已被同步，則不再響應，返回值為空；否則，根據字典中尚未標記同步的頂點查找頂點值以響應同步備份頂點值并更新字典內容.2 階段同步機制顯然可以根據字典信息避免冗余同步，提高響應效率.

3.2.3 實例演示

圖3 展示了按需同步策略下數據存儲和管理方式的一個實例.該實例包含20 個頂點（圖3 中頂點編號直接以數字形式呈現），分布于2 個分布式任務T1與T2.以T1為例，本地圖數據包含頂點v1至v10及其鄰接表，具體分為2 個塊，分別包含頂點v1至v6和v7至v10.對應地，出邊按照目的頂點的分塊信息按列分割存儲.如v1的出邊指向4 個目的頂點，其中目的頂點v2和v3屬于同一個頂點塊，故對應出邊被存儲到同一列中；同理，v7和v18分別屬于不同頂點塊，故對應出邊被存儲在另外2 列中.特別地，v6，v7，v10分別有邊遷移到任務T2,即在T2上存在備份.以為v6例，其出邊〈v6,v13〉和〈v6,v15〉被遷移到T2并按照目的頂點的分塊信息進行按列分割存儲，而遷移之后，T1的響應字典中應添加1 條v6指向T2的記錄.在第k步迭代中，假設T2上的頂點塊v11至v15欲更新頂點值，則分2 步拉取所需消息：1）本地備份消息，即首先檢查本地是否有來自T1的遷移邊，如有，則向T2發送同步請求，而T1收到請求后，首先檢查字典中T1對應的列是否均為1，否則，如有且字典中對應值為0（如此處的v6與v7），則應封裝對應頂點值進行響應并將字典中的值更新為1（此處即v6與v7在T2列的值），而T2收到同步值之后根據遷移邊按需生成本地備份消息；2）非備份消息，可按照原有pull 框架設計，發送消息拉取請求并通過掃描對應列的出邊信息生成消息并返回給T2.當頂點塊v16至v20被調度更新時，可重復此過程，但需要注意的是，v16的更新依賴于v7的消息，但v7的頂點值已經被同步（即T1中字典的對應值為1），故該值不會被再次返回，以避免冗余同步，減少網絡通信開銷.

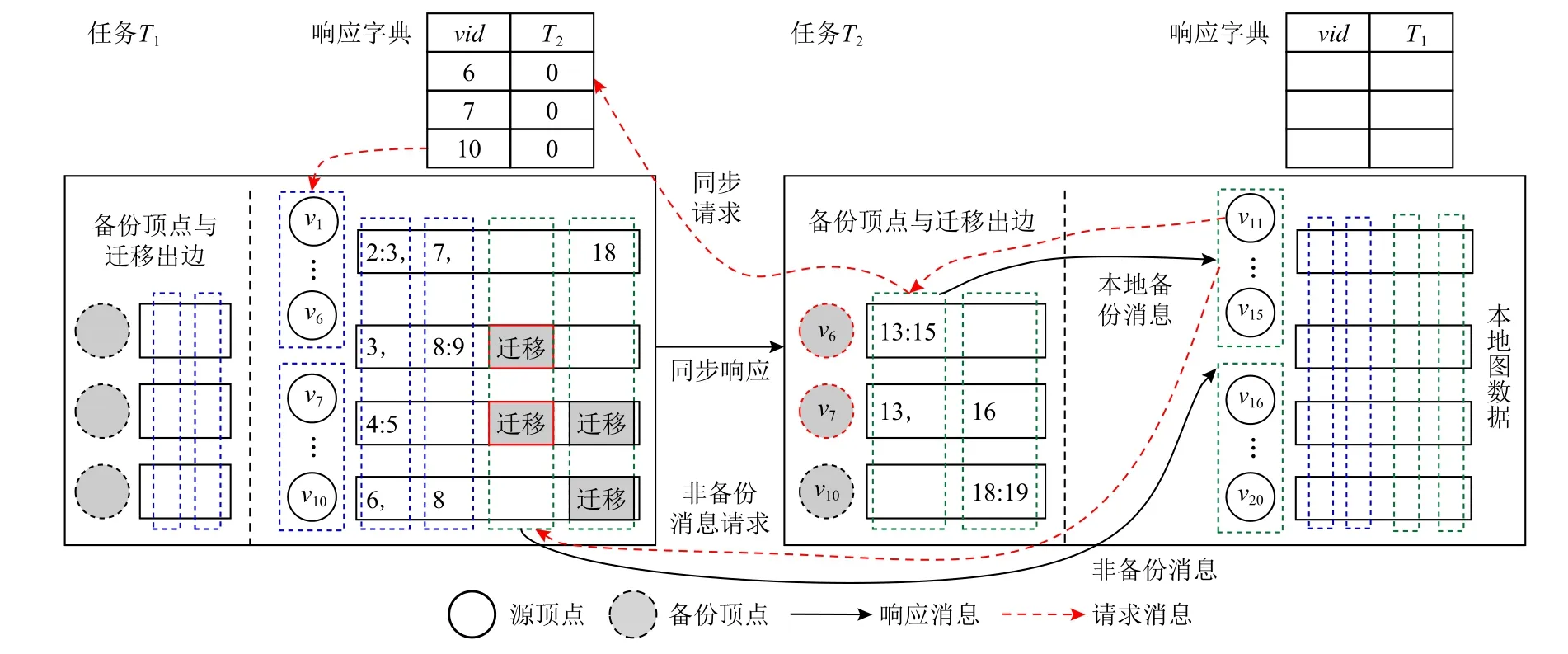
Fig.3 The data storage and management methods of on-demand synchronization update strategy圖3 按需同步更新策略的數據存儲和管理方式

3.3 基于優先級拉取的并發消息生成

在按需同步備份更新策略下，頂點更新所依賴的消息包括備份消息和非備份消息.為獲取這2 類消息，直觀的解決方案是并發發送備份值同步請求和非備份消息請求（詳見圖3 示例）.然而，這種方案的弊端是頂點同步值和非備份消息值的同時傳輸會增大瞬時通信負載，造成網絡擁堵；而在目的任務接收到響應的備份頂點同步值和非備份消息值后，迭代計算的負載重心轉為備份消息的本地生成以及目的頂點更新，均不涉及網絡通信，導致網絡資源空閑.本節介紹基于優先級拉取的并發消息生成策略，通過備份頂點值和非備份消息值的錯峰拉取，提高網絡資源使用效率.

3.3.1 優先級錯峰拉取

基于優先級錯峰拉取和并發拉取的區別在于，前者優先拉取備份頂點的同步值，然后拉取非備份消息且同時啟動本地備份消息的生成與合并處理工作，最后待所有需要的消息準備完畢后，進行目的頂點的計算更新.該方案的優點是不同優先級的拉取請求錯峰響應，消息在網絡中的傳輸壓力減小，且減少了空閑等待狀態，充分利用網絡通信帶寬.

3.3.2 優先級動態調整

給定一個目的頂點塊，由于響應字典的存在以及算法本身消息規模的動態變化，會導致需要拉取的備份頂點同步值以及非備份消息值的規模動態變化.直觀地，當兩者的規模較低時，優先級錯峰拉取可能導致兩者各自均無法充分利用通信帶寬，降低網絡資源使用效率.式（2）和式（3）分別描述了并發拉取和優先級拉取的性能度量方法.

無論采用何種拉取策略，具體工作負載均包括拉取非備份消息值的開銷 φmsg和拉取本地備份消息的開銷，而后者可細分為同步備份頂點值開銷 φsyn和本地備份消息生成開銷 φpro.對于并發拉取，由于2 種拉取請求同時發送、同時響應，故其性能指標 φcon取決于 φmsg與 φsyn+φpro中的較大值，而考慮到同時請求產生的網絡擁堵，應添加懲罰因子 λ(λ ≥1);對于優先級拉取，同步請求被優先發送，而后并行執行備份消息的拉取以及本地備份消息的生成，故其性 φpri能應在 φsyn的 基礎上累加后兩者的最大值，即當 λ較低，比如 λ=1時，顯然有 φcon＜φpri,即并發拉取優于優先級拉取；反之，當 λ較高，即備份頂點值和非備份消息值規模較大而導致網絡擁塞程度加劇時，優先級拉取優于并發拉取.在實際運行圖迭代計算時，可根據算法的執行進度和網絡瞬時狀態，實時計算 φcon與 φpri的 對比結果進而選擇 決定是否將同步請求的優先級升高.具體地，對于需要同步的備份頂點值的規模，可在請求發起端（如圖3 中的任務T2）記錄當前迭代步已經完成同步的備份頂點，當啟動一個新的目的頂點塊的更新時，可先分析本地遷移邊以確定需要同步的備份頂點數目，然后對比已經完成同步的備份頂點，以估算同步開銷；同理，可根據本地遷移邊規模估算本地備份消息的生成開銷；對于非備份消息的規模，因該類消息由其他所有任務生成，相關統計信息無法在本地獲取，故可在迭代計算過程中，通過記錄上一個迭代步中獲取的消息規模來估算本步的消息規模[28]；而對于 λ,可通過測試給定集群在不同擁塞程度下的通信延遲并記錄整理為先驗知識，直接帶入公式進行對比分析.

3.4 頂點備份方式討論

圖劃分是分布式圖計算的基礎，而劃分技術可分為邊割與點割兩大類.邊割的核心是以頂點為中心進行圖劃分，即將頂點分配到各計算任務；如果一條邊的2 個頂點位于不同任務，則該邊成為切割邊，在迭代計算過程中會引入通信開銷；因此在頂點分配時應考慮切割邊的規模以優化通信開銷，Pregel 等系統均以邊割方式運行圖算法[11].點割的核心是以邊為中心完成圖劃分，即將邊分配到各計算任務；如果同一個頂點關聯的2 條邊位于不同任務，則該頂點被切分，且多個切分點中會隨機選擇一個作為主控頂點master 而其余作為切分后的從節點mirror 存在，在迭代計算過程中的通信僅發生在master 與mirror之間.顯然，邊分配的過程應盡量減少頂點被切分的概率.PowerGraph 等系統以點割方式運行圖計算[9].

本文的頂點備份是在邊割基礎上進行的通信優化.給定邊割的圖劃分結果，也即頂點在任務間的分布已經確定，備份機制將對每個頂點v（master）的出邊進行解析，通過分析其目的頂點在任務間的分布來評估后續計算過程中的通信開銷；如果v與任務Ti間的通信過高（即指向Ti中頂點的出邊數目超過閾值θ），則將v中對應的邊定向遷移到Ti中并在Ti進行v的備份（mirror）.

基于以上描述，本文備份框架與點割方案中，雖然頂點均存在master 與mirror 的功能角色之分，但在備份的主動性和方向性方面存在區別.

1）備份的主動性.在基于邊割的頂點備份優化框架中，由于頂點（master）分布已經確定，可精確分析“頂點—任務”之間的通信開銷并主動決定是否進行出邊遷移與頂點備份；而點割方案中，采用啟發式規則來指導邊的分配并在分配過程中直接（被動）完成頂點切分（以及master 和mirror 的界定），由于邊分配是動態完成的，系統無法主動分析通信收益以決定是否進行頂點切分.

2）備份的方向性.在基于邊割的頂點備份框架中，由于頂點備份是因遷移出邊而引起的，故備份的頂點均作為邊的起始點而存在，也即僅將高出度頂點v（master）切分為若干備份頂點（mirror），當v（master）向其出度鄰居廣播消息時，可先通過網絡將v（master）的值同步到備份頂點（mirror）再由備份頂點進行局部廣播，即將消息傳遞給目的頂點，從而優化通信開銷；而在點割方案中，為保證同一個任務上的子圖完整性，備份頂點（mirror）既可能作為邊的起始點存在，也可能作為邊的終止點存在，邊的起始點可將發往頂點v的消息首先在其各任務的mirror 上進行局部計算以減輕v（master）的處理壓力（如PageRank 算法中，可基于mirror 進行消息的局部累加和操作），邊的終止點可減少v（master）向其出度鄰居廣播消息時的通信開銷.

下面分析本文舍棄點割，轉而基于邊割機制設計頂點備份優化機制的原因.

1）從備份的方向性角度.針對本文關注的多維消息類算法，消息值通常不滿足累加特性，即無法將多個消息值通過計算合并為一個消息值（如PageRank中的累加求和，以及最短路徑計算中的最小值計算），而只能將消息值進行簡單串聯連接（即本文表1 中的值連接類算法），此時點割機制中，作為起始點存在的mirror 不但失去“先局部計算以減輕v（master）處理壓力”的意義，反而引入了mirror 的存儲開銷與維護開銷.另一方面，本文相關技術基于以塊為中心的pull 框架實現，其基礎框架可保證各頂點發送的消息在發送端實現“能合并盡合并”[10]，故即使針對單維值可合并的多維算法（如MSSP），可以Combine 合并的方式在發送端實現消息的局部合并，且僅在運行時使用，無需始終維護mirror.

2）從備份的主動性角度.基于邊割的頂點備份可保證被備份的頂點均可帶來通信收益，而點割機制由于邊分配的動態性，無法保證備份的通信收益.此處，注意到PowerLyra[20]基于PowerGraph 的點割進行了混合備份優化（hybrid-cut），即通過閾值設定，僅針對高度頂點進行點割而對于低度頂點保持邊割.這與本文對高度頂點進行切分，以最大化減少網絡通信開銷的目的是一致的.然而，本文是在邊割基礎上完成頂點備份，而PowerLyra 是在點割基礎上進行優化.顯然，兩者在備份方向性的2 個角度存在區別.具體地，從頂層設計層面，本文和PowerLyra 均針對高度頂點進行切分，這必然涉及到“高度”的衡量標準，即備份閾值θ.從實現層面，本文的 θ作用于頂點v指向任務Ti上目的頂點的出邊規模，而非PowerLyra 中作用于v的全部出邊（即出度）.由于出邊規模超過閾值即會產生備份，考慮到高出度頂點指向某個具體任務的出邊也可能較少，顯然本文的作用域更為精確，可確保通信收益.其次，PowerLyra 并未給出閾值θ的推薦方式，僅以多次重復實驗的手工方式選擇較優閾值；而本文在第4 節分析了遷移導致的負載偏斜代價與通信收益，可基于統計信息給出推薦的最優閾值并在5.4 節通過大量實驗驗證了相關方案的可行性.

下面通過實例分析，展現本文備份機制的輕量級特點.假設分布式任務的數目為3，圖4 給出了一個包含6 個頂點、9 條邊的示例圖在PowerLyra 和本文輕量級備份框架下的備份情況分析.設定備份閾值θ=3，PowerLyra 以邊表的方式并行加載輸入圖并根據邊的源頂點的Hash 值，即Ti=hash（exy.x-1）%3，決定該邊的分配位置.然后統計各頂點的出度，如果出度值大于等于3，則認定為高度頂點，則按照該頂點關聯出邊的目的頂點重新分配出邊，即Ti=hash（exy.y-1）%3.這里頂點v1被判定為高度頂點，其出邊e12與e15被遷移到任務T2，而e13被遷移到任務T3.最后按照備份方向性的討論，完成頂點備份，即T1中 的v3，T2中 的v1以 及T3中 的v1與v2.然 而，T2中的v1顯然無法進行通信優化，因為v1在該任務上僅有一個目的頂點，備份與否并不能優化通信規模.這是由于點割方案無法主動控制頂點切分而導致的現象.相反地，本文輕量級備份以鄰接表作為輸入，并利用Range 劃分按照字節規模均衡分割、并行加載.而對于高度頂點的界定，采用“頂點—任務”模式進行主動界定.此處，只有頂點v1向任務T2進行邊e12，e13，e14的遷移并備份v1，因為v1指向T2的出邊數目大于等于閾值θ，從而保證通信收益.注意到在本文備份機制下，出邊被遷移后，任務T2的負載加重，而其中的偏斜程度與閾值的設定相關.第4 節將詳細討論閾值的設定問題.

綜上，基于本文關注的多維消息算法的巨大內存開銷，以及以塊為中心的、最新的pull 系統框架，考慮到點割的維護開銷和通信收益的不確定性，本文基于邊割的圖劃分技術，通過頂點備份進行通信再優化.故本文備份機制的輕量級特點，可總結為4 點：1）優化的pull 同步方式可顯著減少備份頂點同步過程中的內存開銷并與普通消息的pull 方式統一，便于系統級優化（如容錯控制）；2）僅按照出邊方向進行頂點備份，減少備份開銷；3）通過精確控制備份閾值的作用范圍，避免無效的冗余備份，保證通信收益；4）提供備份閾值的自動優化計算模型，避免頻繁手動測試的閾值選擇方式.

4 自適應性能優化模型

本文基于Range 劃分完成邊割，而Range 方法將輸入圖（由頂點和出邊組成）的數據規模進行均等切分，可保證各計算節點負載（即頂點和出邊的數量之和）的均衡性.在此基礎上，頂點備份框架在圖劃分階段額外引入各任務間頂點的備份和出邊的遷入遷出等操作.考慮到真實圖的度分布通常有冪律偏斜特點，備份頂點在各任務間的分布也具有偏斜，且每個任務遷移邊的規模不盡相同，這顯然破壞了原Range劃分的負載均衡.故本文設計的框架對負載均衡方面沒有改善，大部分情況下甚至會加重負載偏斜.

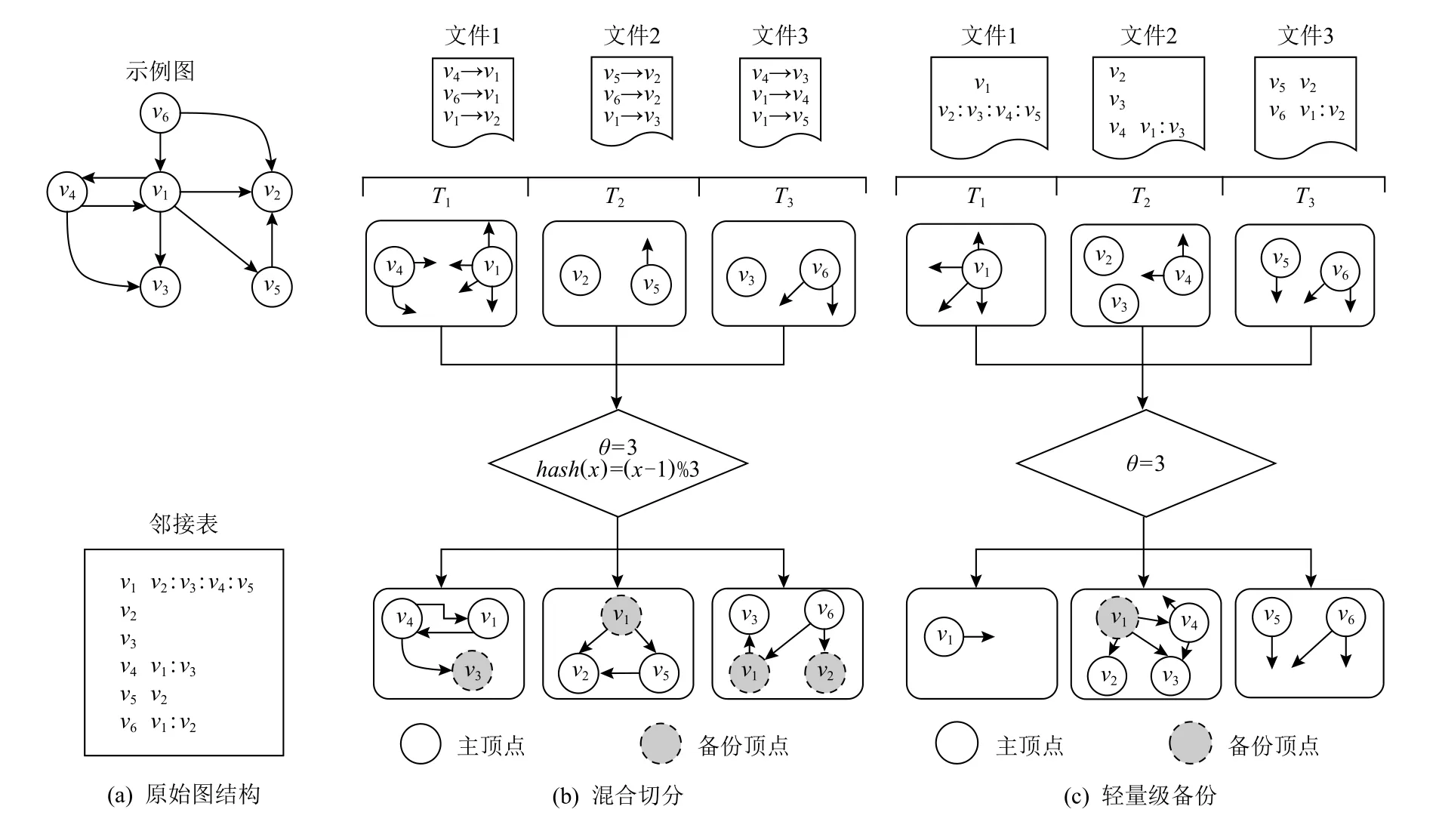
Fig.4 Comparison of hybrid-cut and lightweight vertex replication圖4 混合切分與輕量級頂點備份的對比

在頂點備份機制中，位于任務Ti上的頂點v是否需要在任務Tj上進行備份，取決于其出邊是否被遷移.直觀地，如果v的鄰接表中存在大量指向Tj上目的頂點的出邊，則邊遷移可顯著降低通信代價，但同時也會引起Ti與Tj的負載變化進而影響性能.因此，需要根據通信收益和負載影響綜合考慮，設定出邊遷移閾值θ,當指向Tj的出邊數目超過 θ時，證明通信收益可抵消負載變化影響，允許遷移，否則禁止遷移.顯然 θ的設定對備份機制的實際性能收益至關重要.在實際應用場景，可通過多次運行迭代算法手動尋找最優閾值，但這會浪費大量計算資源，可操作性較差.一種理想的方式是給出 θ相關的性能函數，然后自動分析最優閾值以指導實際算法的運行.本節重點介紹一種基于線下先驗知識與線上實時信息相結合的閾值計算模型，其中4.1 節介紹預測函數，而4.2節介紹重要參數的線下與線上獲取方式.

4.1 出邊遷移閾值優化預測函數

輕量級頂點備份框架的性能預測指標要綜合考慮頂點備份后的通信凈收益和備份前后各任務負載均衡程度變化導致的水桶效應影響.給定遷移閾值θ,式（4）給出了性能預測函數的邏輯結構，其中 φcom表示頂點備份后的通信凈收益，而φload代表備份前后各任務的負載均衡變化引起的水桶效應影響.

對于通信凈收益 φcom,由第3 節可知，頂點備份在產生消息通信收益的同時，會引入備份頂點值的同步開銷.其中，消息通信收益取決于頂點備份所產生遷移的出邊數量（E上面的橫杠表示備份）以及沿出邊發送的消息字節大小 ηmsg，而同步開銷則取決于備份頂點的數量和被同步的頂點值字節大小從字節規模角度給出了通信的凈收益.需要注意的是，分布式網絡通信的基本流程是首先在發送端進行數據序列化，然后將序列化后的數據通過網絡傳輸到接收端，接收端進行反序列化操作之后即可得到可用數據.因此，在得到消息總規模和同步數據總規模后，可根據網絡傳輸速率Snet和接收端、發送端的序列化、反序列化速率Sio來計算凈性能收益 φcom：

其中，P代表共同參與計算的分布式任務數目，式（5）等號右邊第1 項為分布式環境下的凈性能收益；序列化和反序列化需要在發送端和接收端分別執行，因此需要將字節規模乘以系數2.

對于負載均衡變化導致的水桶效應影響 φload,考慮到某個任務Ti在向其他任務遷移出邊的同時，也在接收其他任務遷入的邊數據.這種遷入遷出會打破既有圖劃分結果的均衡性，進而影響負載偏斜程度，導致水桶效應延遲發生變化.分布式環境下，系統處理性能取決于負載最重的任務，因此可用備份前后最重負載的差值作為衡量指標.若備份后的負載均衡狀況優于備份前，則負載指標的計算結果為正，對處理性能起正向加速作用；反之，則會降低系統處理速度.φload的計算方式為

其中 1 ≤i≤P，1 ≤j≤P，|Vi|和 |Ei|分別表示計算任務Ti上分配的子圖Gi的頂點數和邊數，而分別表示備份到任務Tj上的頂點數和由頂點備份導致的出邊遷入遷出變化數.此外，無論是本地頂點還是備份頂點，在計算更新或同步更新時，會產生計算負載，因此分別加入調節因子 α 和 β以調節其相對于邊操作的負載.其中，α的值取決于頂點的計算更新以及遍歷參與計算更新的接收消息的復雜度；β的值取決于備份頂點的同步更新.顯然，α 和 β的值由算法和數據集共同確定.最后，Stpt為系統吞吐效率，可在給定集群上通過運行標準測試程序獲得.

4.2 關鍵預測參數的獲取

根據式（4）～（6）,當 φ為正值時可提高計算效率，而 φ的預測值主要取決于4 類參數：1）遷移與備份相關類參數，具體包括備份頂點數,遷移邊數,和圖劃分結束后各任務的子圖分布 |Vi|與 |Ei|,其中 |Vi|與 |Ei|的取值依賴具體的圖數據集拓撲結構以及分布式任務數目P,而備份與遷移參數還與備份閾值 θ密切相關；2）應用算法類相關參數，主要包括 ηval，ηmsg,其取值由應用層面的圖迭代算法決定；3）硬件配置類參數，即Snet,Sio，Stpt,可通過在給定集群上運行標準測試程序獲得；4）權重調節因子 α 和 β,可通過分析應用算法復雜度與圖數據集的平均出入度計算得到.在上述4 類參數中，第3 類屬于固定常量，只要集群的硬件配置不變，無需反復測試，較易獲取和維護；第2 類和第4 類與具體的應用算法和數據集相關，需要根據用戶提交的作業程序實時分析，屬于較易獲取的線上實時參數；第1 類因涉及圖拓撲結構以及關鍵變量θ,難以通過直觀的理論分析進行準確估計，因此本節對第1 類參數的獲取進行詳細討論.

雖然第1 類參數難以理論評估，但注意到其只與數據集和集群任務配置相關，而與具體的應用算法無關.考慮到具體領域的圖應用通常是根據指定的數據集進行多方位的挖掘分析，如社交網絡公司對其運營的社交網絡圖進行社團聚類、廣告推薦以及成員影響力評估等多種業務分析，論文檢索系統對學術研究網絡進行合作研究團隊識別、新研究領域發現以及學界泰斗與新星挖掘等業務分析.這表明，針對一個數據集，通常會從不同角度進行不同類別的應用分析，即多次在同一個數據集上運行不同算法.因此，可對給定的數據集和任務數目配置，通過線下變換 θ值統計不同任務上的第1 類參數值并保存為先驗知識.當需要在指定數據集上運行某種算法時，可依據先驗知識和算法相關的實時信息，立即計算出較優的備份閾值，指導輕量級備份框架的運行.

在參數提取階段，僅需統計各任務的備份頂點數目以及遷移邊交換情況，而無需進行具體的迭代計算.因此可直接利用分布式圖處理系統的數據加載流程進行邏輯數據統計，而不必進行實際的物理遷移與頂點備份操作，以節省參數提取開銷.邏輯統計的另一個優勢是，可同時分析多個 θ取值下的參數數值，避免針對每個閾值取值進行一次參數提取，進一步壓低提取開銷.下面通過算法1 介紹第1 類參數的具體提取過程.

算法1.備份頂點和遷移邊數目統計.

算法1 展示了P個分布式任務中某個任務Ti的運行流程.該任務對給定的劃分子圖Gi,分析各種備份閾值 Θ={θ1,θ2,…}下的頂點備份與遷移邊數目等統計信息.具體地，通過遍歷Gi中的每條鄰接表記錄，統計其出邊所指向的目的頂點在P個任務之間的分布頻數并記錄在數組dstTid中（行⑥～⑨）；之后分析不同閾值設定下如 θj,是否向對應的任務如Tk進行出邊遷移以及頂點備份，如是，將該統計信息記錄在各閾值下備份頂點數以及遷出出邊數的分布矩陣Mi與Ni的第（j,k）位置（行⑩～?）.需要注意的是，此處僅統計分布信息，而無需對邊進行實際物理遷移（行?），因此算法1 的運行效率較高.

5 實驗結果與分析

5.1 數據集與實驗設置

本文在支持完全合并的HGraph 系統上實現了輕量級頂點備份框架，可同時支持消息完全合并以及源頂點備份，在繼承HGraph 系統優勢的前提下，實現備份機制的內存優化和通信性能提升.為便于區分，實現輕量級按需備份的系統被稱之為LGraph（light-weight graph）.實驗設計方面，首先在不同數據集上對比輕量級頂點備份與傳統push 備份的內存使用占比（5.2 節），然后給出輕量級頂點備份與HGraph原系統的性能對比與分析（5.3 節），最后驗證自適應性能優化模型的預測分析結果以及備份過程對性能的影響（5.4 節）.應用算 法選取 表1 中多維算法MSSP,SC,SA，分別作為合并類和連接類的代表.其中MSSP 與SC 的算法邏輯已在2.2 節中介紹.而SA算法是基于LPA 設計完成的廣告傳播模擬算法，即每個頂點維護自己感興趣的廣告標簽列表，迭代開始后，各頂點根據入度鄰居的廣告喜好分布對自己的廣告列表進行更新并廣播給出度鄰居，其消息值不可合并且消息值需要使用多個int 數據來表征廣告標簽.當涉及運行時間分析時，由于SC 與SA 算法在每步迭代中所有頂點均激活并向所有出度鄰居廣播消息，各步的負載相同，故除非特殊聲明，否則僅匯報一個迭代步的運行時間；而對于MSSP，各步激活頂點規模動態變化，導致負載也不盡相同，因此匯報整個算法收斂的總迭代計算時間.

實驗集群由5 臺小型服務器組成，包括4 個計算節點和1 個主控節點，節點配備千兆網卡并使用千兆交換機互聯，實測網絡傳輸性能為89 MBps①網絡性能測試使用iperf-2.0.5 工具.主控節點配置Intel i9-10900K，3.7 GHz 的10 核CPU,1 TB固態硬盤，64 GB 內存；每個計算節點配置Intel 至強E3-2224，3.5 GHz 的4 核CPU,1 TB 機械硬盤，32 GB內存.實驗使用4 個真實圖數據集，各數據集的具體信息描述如表3 所示.

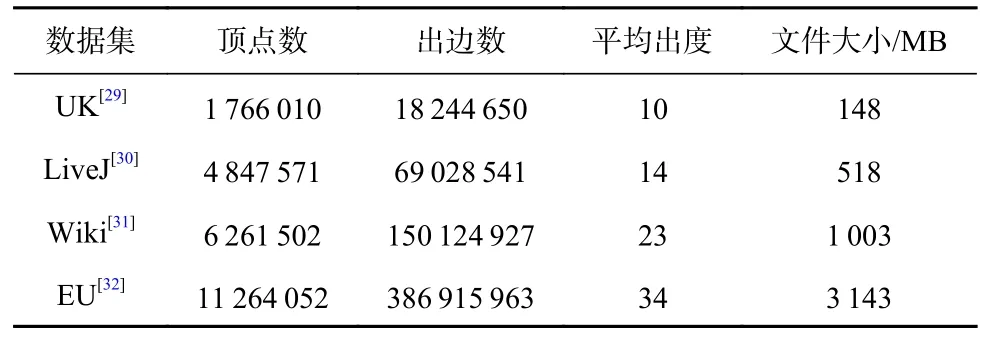
Table 3 Description of Real Datasets表3 真實數據集描述

實驗參數設定方面主要涉及閾值優化模型，其中網絡通信與序列化/反序列化速率為Snet=89 MBps,Sio=507 MBps,平均負 載吞吐率為Stpt=42 MBps；另一方面，負載權重調節因子 α=(μin·ηmsg)/Supd,β=(μout·ηval)/Supd，其中 μin與 μout分別為對應數據集的平均入度與平均出度，Supd為頂點更新/同步的CPU 處理速度，實測值為1533MBps.最后，對于MSSP 類算法的并發源頂點數目設置，考慮到其合并與備份的通信收益之差與并發粒度成正比，同時在真實應用環境下通常在硬件允許的前提下采用較大的并發粒度以提高圖遍歷共享收益，故在UK 和LiveJ 數據集上將并發粒度直接設置為平均出入度值；而對較為稠密的高出入度圖Wiki 和EU，將并發源頂點數目設置為平均出入度的2 倍，以強化通信收益.

5.2 備份頂點同步模式對比

本節在4 個真實數據集上對比了傳統push 同步頂點備份方式與按需同步頂點備份方式的內存使用占比情況（即push 同步的內存消耗/按需同步的內存消耗）和同步性能，以證明按需同步頂點備份方式在減少內存資源消耗方面的同時還可以保證相近的同步性能.表4 和 表5 分別展 示了連 接（SC）和合并（MSSP）類多維消息算法的對比結果.由于按塊拉取框架的消息按需生成，因此不同的頂點分塊數目決定了按需生成消息的規模.故測試過程中，通過將每個任務上的頂點分塊數目由2 增加到64，觀察2 種同步方式的內存消耗變化.

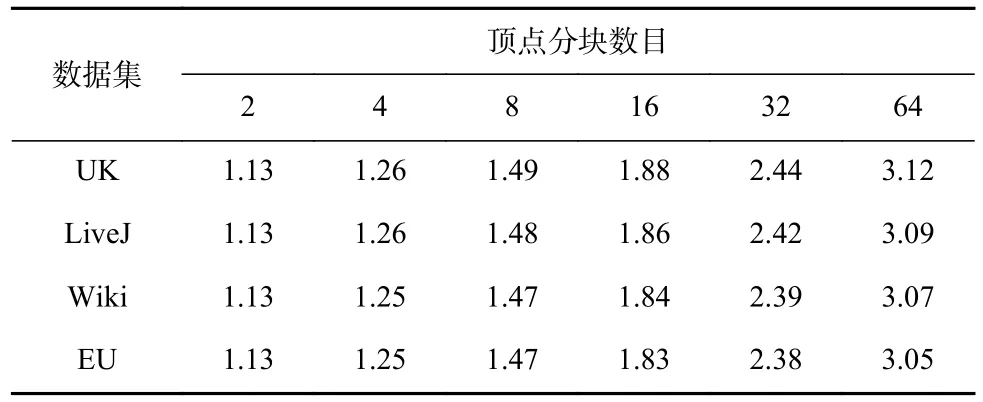
Table 4 Memory Usage of Concatenation Algorithms表4 值連接類算法內存使用情況

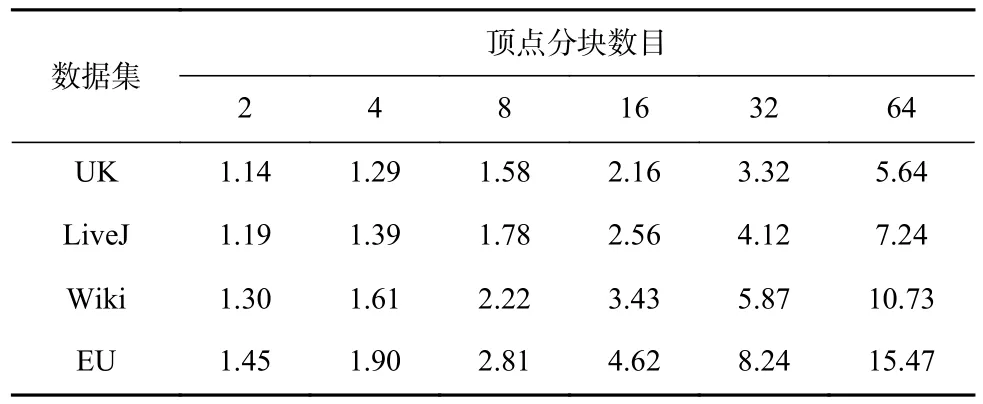
Table 5 Memory Usage of Combination Algorithms表5 值合并類算法內存使用情況

在2 類算法中，按需同步的備份方式均表現出更低的內存使用情況（對比值均大于1）.這是因為按需同步備份方式節省了發送端和接收端的多緩存以及本地消息接收緩存設置.隨著每個任務上的頂點分塊數的增加，每塊內部的頂點規模下降，其接收的消息規模也隨之成比例下降，導致按需生成的消息規模降低，內存消耗減少；與此同時，push 同步方式的發送與接收端緩存，只受任務數目的影響，不隨頂點分塊的變化而改變.因此，隨著塊規模的增大，在不同數據集和算法的所有組合測試案例中，兩者的內存消耗對比值均呈現增加趨勢.此外，對于MSSP，因不同數據集下其并發源頂點數量的不同，每條消息的大小也會發生變化，導致不同數據集下內存收益表現出較大的差異性.特別地，EU 數據集上的MSSP算法并發源頂點數量最多，需要消耗大量內存，故在頂點分塊為64 時2 種方案的內存消耗對比最為明顯，此時push 同步的內存消耗規模約是本文方法的15 倍.因此，對于消息規模巨大的多維消息類算法，采用本文的按需同步方式可有效降低消息傳遞的規模，從而減少系統的內存資源消耗.

在同步性能分析方面，由于備份頂點的同步操作與正常消息值的交換操作緊密耦合，難以剝離出同步操作的精確時間開銷.考慮到同步方式的不同，僅影響同步性能而不會影響正常消息的操作效率以及頂點更新效率，此處采用控制變量法，即設定其他參數均一致而僅變化備份頂點的同步方式，然后通過匯報迭代計算過程的運行時間來反映不同同步方式的性能影響.如表6 所示，通過手動測試不同備份閾值下LGraph 的運行時間來確定最優閾值，然后以最優閾值作為輸入，測試不同同步方式下的運行時間.這里，npull 是未采用3.3 節中優先級技術的拉取操作方案而pull 是集成優先級技術的方案.雖然pull方式涉及同步請求發送環節，但受益于同步字典的冗余消除剪枝作用以及優先級調度，其同步效率與push 方式幾近相同（延遲率 ＜2%）.綜合表4～6 可知，本文的pull 同步方式在不影響同步效率的前提下可顯著優化內存使用開銷，從而提升系統在數據處理容量方面的擴展性.

5.3 備份性能分析

本節分別在4 個真實數據集上運行3 種多維消息類算法，通過手動測試不同備份閾值下LGraph 的運行時間并選擇與最優閾值下的性能與無備份機制的HGraph 進行對比，以展現輕量級備份框架的最佳性能收益.由于算法和數據集本身存在的復雜性和冪律偏斜特性，每組實驗的實際收益各不相同，圖5～7 分別展示了對比效果.

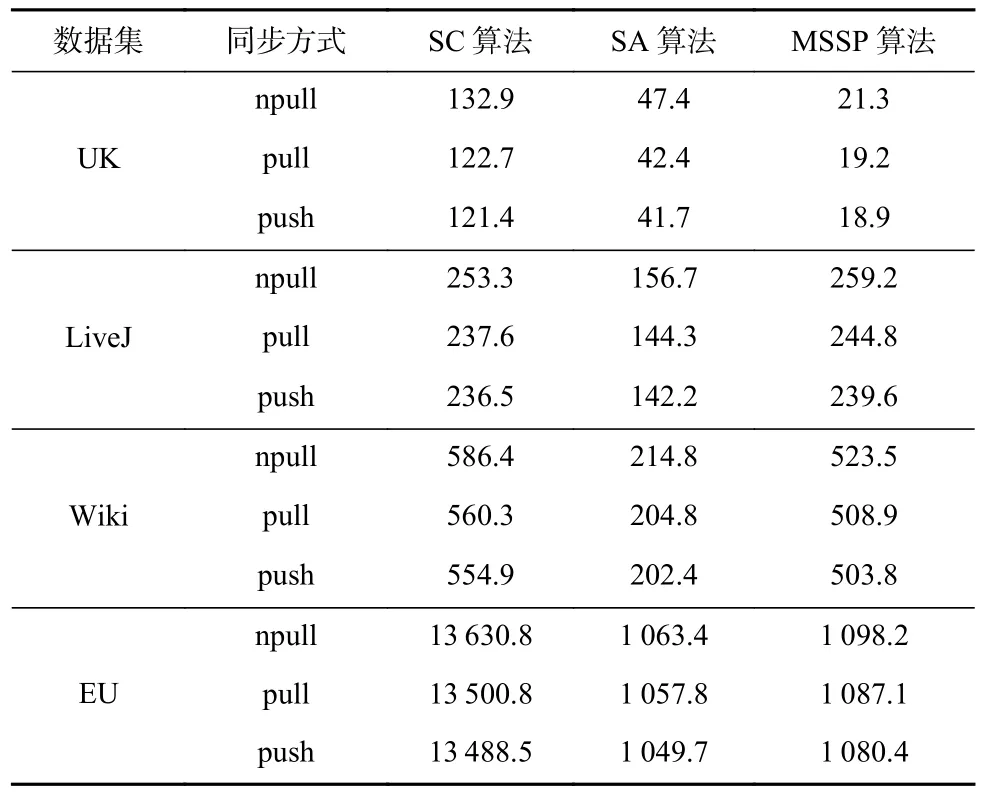
Table 6 Comparison of Synchronizing Running Time for Replicated Vertices with pull and push表6 pull 與push 方式下備份頂點的同步運行時間對比 s

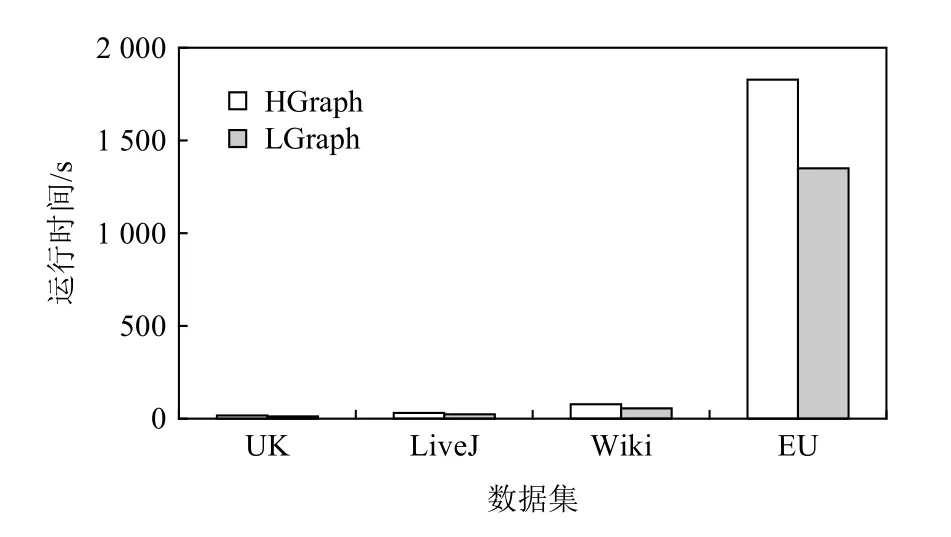
Fig.5 Running time of SC algorithm on different data sets圖5 SC 算法在不同數據集上的運行時間

Fig.6 Running time of SA algorithm on different data sets圖6 SA 算法在不同數據集上的運行時間

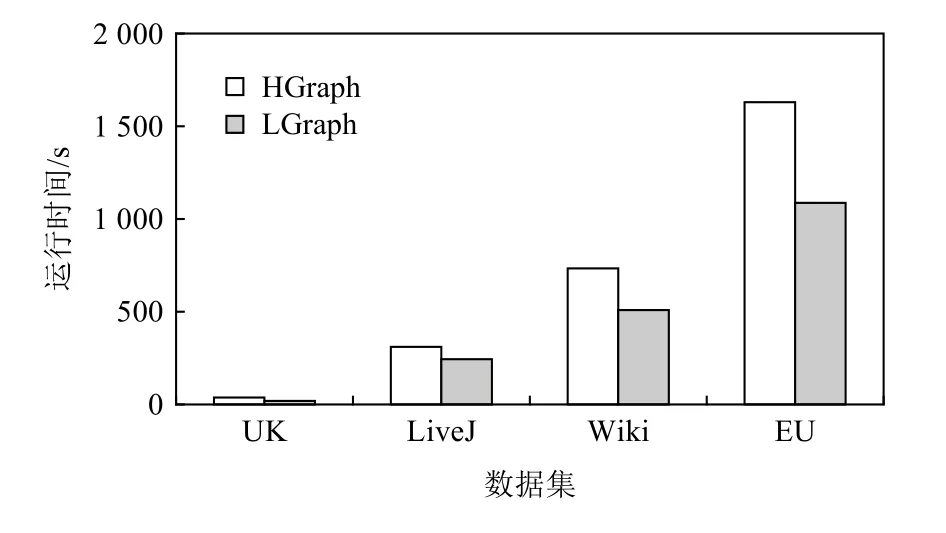
Fig.7 Running time of MSSP algorithm on different data sets圖7 MSSP 算法在不同數據集上的運行時間

在算法和數據集的各種組合中，LGraph 的計算時間始終低于HGraph.特別地，對于連接類算法SC和SA，由于其只能合并目的頂點ID，消息合并收益對整體性能提升并不敏感.換言之，通信性能的優化主要依靠頂點備份.此時通過選擇較好的備份閾值，可以顯著提升整體性能，如SA 算法在Wiki 數據集上可以達到53%的性能提升.對于可合并類算法MSSP，在UK 和LiveJ 數據集上，可實現24%和21%的性能提升；而對數據集Wiki 和EU，由于并發源頂點數目增大，此時性能收益可分別達到31%和33%.

針對各數據集上的不同算法，圖8 和圖9 分別匯報了最優備份閾值對負載和通信的影響，即4.1 節中分析的因負載偏斜導致的水桶效應 φload以及因備份帶來的通信收益 φcom.需要注意的是，實際運行圖計算作業時，水桶效應和通信收益同時發生，兩者對運行時間的影響緊密耦合，無法精確測量各自的實際影響.故此處匯報的 φload與 φcom均為量化后的理論估算的運行時間（單位為s），以展示備份后的負載偏斜代價和通信收益，進而理解本文技術可加速圖計算過程的原理.

圖8 中，頂點備份對負載變化的影響是指計算過程中水桶效應拖慢的系統運行時間.LGraph 備份后的負載指標計算結果均為負，即備份后的負載均衡情況劣于備份前，對加速圖計算過程起反向作用.根據式（6），負載變化與拓撲結構和消息維度規模密切相關.從拓撲結構角度來看，Wiki 數據集由于出/入度偏斜指數相差較大，頂點的備份和邊的遷入遷出對其負載影響較大；而EU 數據集的高出/入度頂點較多且在各任務間的分布較為均衡，故備份對負載變化的影響較小.從消息維度角度來看，MSSP 由于并發源頂點數目多，導致消息和頂點值的字節數均大于其余2 個算法，因此其負載變化幅度通常是最大的.特別地，在LiveJ 數據集上，MSSP 算法的負載變化遠小于SA 算法.這是由于算法特性導致兩者的備份閾值不同.根據表7，MSSP 的備份閾值遠高于SA，導致MSSP 參與遷移的邊以及備份的頂點規模均較少，故負載變化較少.

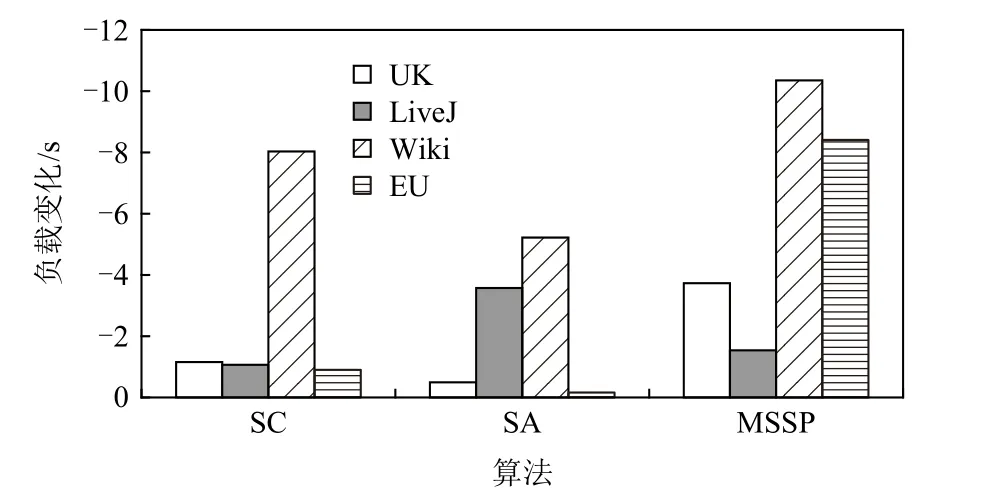
Fig.8 Analysis on workload variation due to vertex replication圖8 頂點備份對負載變化的影響分析

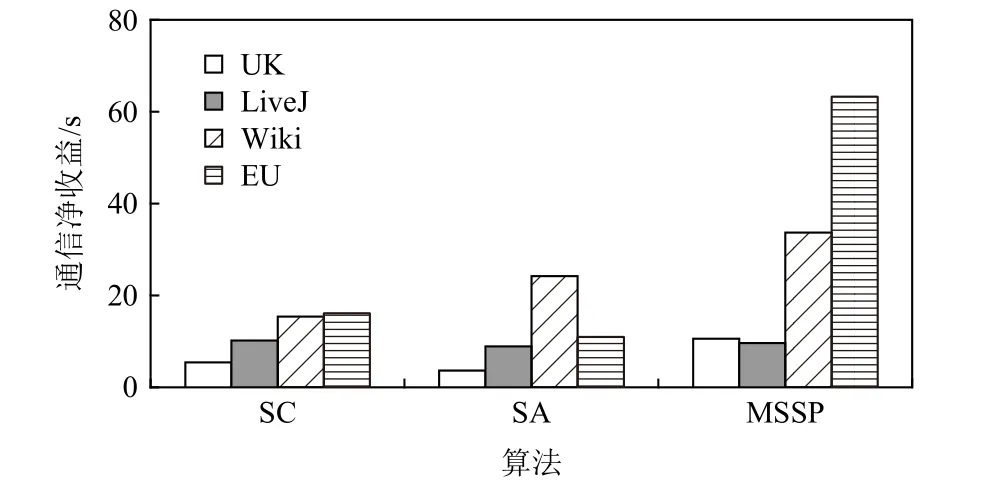
Fig.9 Analysis on communication net benefit variation due to vertex replication圖9 頂點備份對通信凈收益變化的影響分析

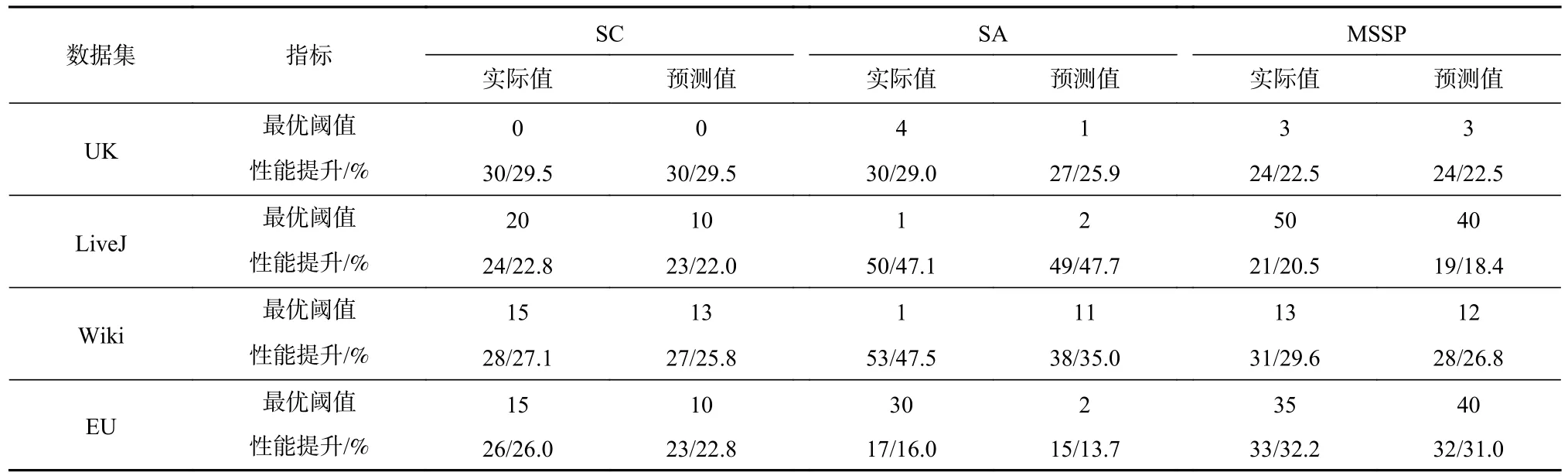
Table 7 Comparison of Performance Improvement Between Actual and Predicted Optimal Replication Thresholds表7 實際與預測最優備份閾值的性能提升對比

頂點備份對通信收益變化的影響是指計算過程中頂點備份加快的系統運行時間，以備份后產生的消息通信收益與引入備份頂點值的同步開銷之差作為最終的通信收益指標，圖9 展示了各算法的通信收益.對比圖8 和圖9 可以發現，不同算法在各數據集上的負載變化與通信收益趨勢一致，即高負載偏斜會帶來較大的通信收益.其中，對于LiveJ 數據集上的MSSP 與SA 算法，由于MSSP 算法備份閾值較高，導致遷移邊的規模降低，故通信收益較少.綜合來看，通信收益與負載代價之差的變化位于3.64～63.26 s 之間，即輕量級頂點備份框架即使引起負載偏斜，仍能提高圖處理的整體性能.

5.4 自適應性能優化模型分析

本組實驗主要驗證備份閾值優化模型的有效性以及所產生的額外開銷.

1）模型有效性.自適應優化模型的有效性可通過2 個方面進行驗證，即公式 φload與 φcom對負載偏斜和通信收益估算的準確性以及最優閾值選擇的準確性.φload的驗證方式為，通過在4 個數據集上運行SC，SA，MSSP 算法，首先手動詳細測試了不同備份閾值下LGraph 的實際表現；對應地，為便于對比，將備份閾值優化模型的輸出結果（即 φload與 φcom理論估算值）累加上無備份的HGraph 的運行結果，從而對備份框架的性能進行理論評估.φcom則通過對比手動選擇的最優閾值與自適應模型計算的最優閾值及其對應的LGraph 性能來驗證.

圖10 展示了φload與φcom的估算準確性驗證.隨著閾值的增加，算法在不同數據集上的運行時間一般呈先下降后上升趨勢，并最終達到甚至超過無備份的HGraph 運行時間.算法整體運行時間的變化，是通信收益與負載偏斜延遲之間相互作用的結果.前期，隨著閾值增大，參與備份的頂點（以及遷移的出邊）規模減少，導致通信收益降低，但同時負載偏斜程度也急劇下降，因此綜合性能收益為正；后期，隨著閾值持續增大，通信收益的損失遠大于負載偏斜的緩解，導致綜合性能收益為負，總運行時間呈持續上趨勢.注意到在大部分情況下，當閾值超過500 時，由于指向某一目的任務的最大出度超過500 的頂點數量極少，頂點備份產生的通信收益趨于0，LGraph的實際迭代性能在此時與HGraph 相當.特別地，對于EU 數據集上的SC 算法（圖10（d））和MSSP 算法（圖10（l）），由于高出度頂點較多，當閾值增大時，仍有大量出邊被遷移，但任務間的負載分布卻更為偏斜，導致通信收益無法抵消負載延遲開銷，使得LGraph實際性能甚至不如HGraph.此時的閾值分析模型雖不能很好地擬合實際性能表現，但也可以預測出整體運行時間呈現上升趨勢，從而指導編程人員避免選擇較大的閾值.整體來看，圖10（a）～（l）表明自適應閾值分析模型可較好地擬合實際運行時間的變化趨勢，為最優備份閾值選擇的準確性提供了保證.

表7 對比了實際手工測試得到的最優閾值與分析模型計算得到的最優閾值，以驗證最優閾值自動選擇的準確性.表7 同時匯報了累加數據加載與劃分開銷后頂點備份對整個作業運行時間的優化效果，即“性能提升”斜杠后面的內容.顯然，閾值分析模型在UK 數據集上的SC 與MSSP 算法、LiveJ 數據集上的SA 算法、Wiki 數據集上的SC 與MSSP 算法均可以找到或近似找到最優閾值；對于LiveJ 數據集上的SC 與MSSP 算法、Wiki 上的SA 算法和EU 上的SA算法，自動計算的最優閾值與實測值相差較大，這是由于收益與延遲開銷的博弈接近臨界值，對各種參數的取值較為敏感，難以準確預測，但也因此導致最優閾值周圍的性能變化幅度較小（見圖10（b）（j）與圖（g）（h）），故即使閾值選擇偏差較大，實際的性能收益仍然接近手動選擇的最優值.

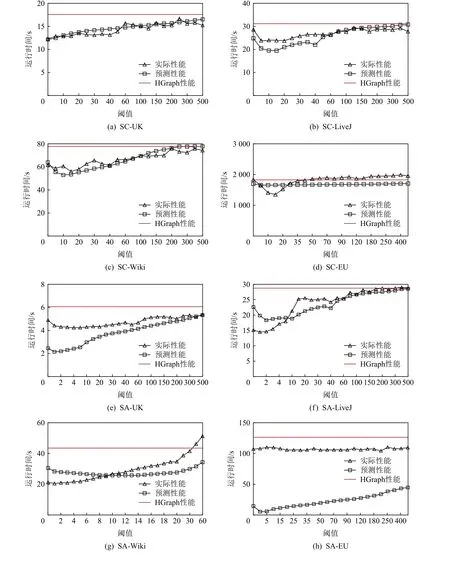
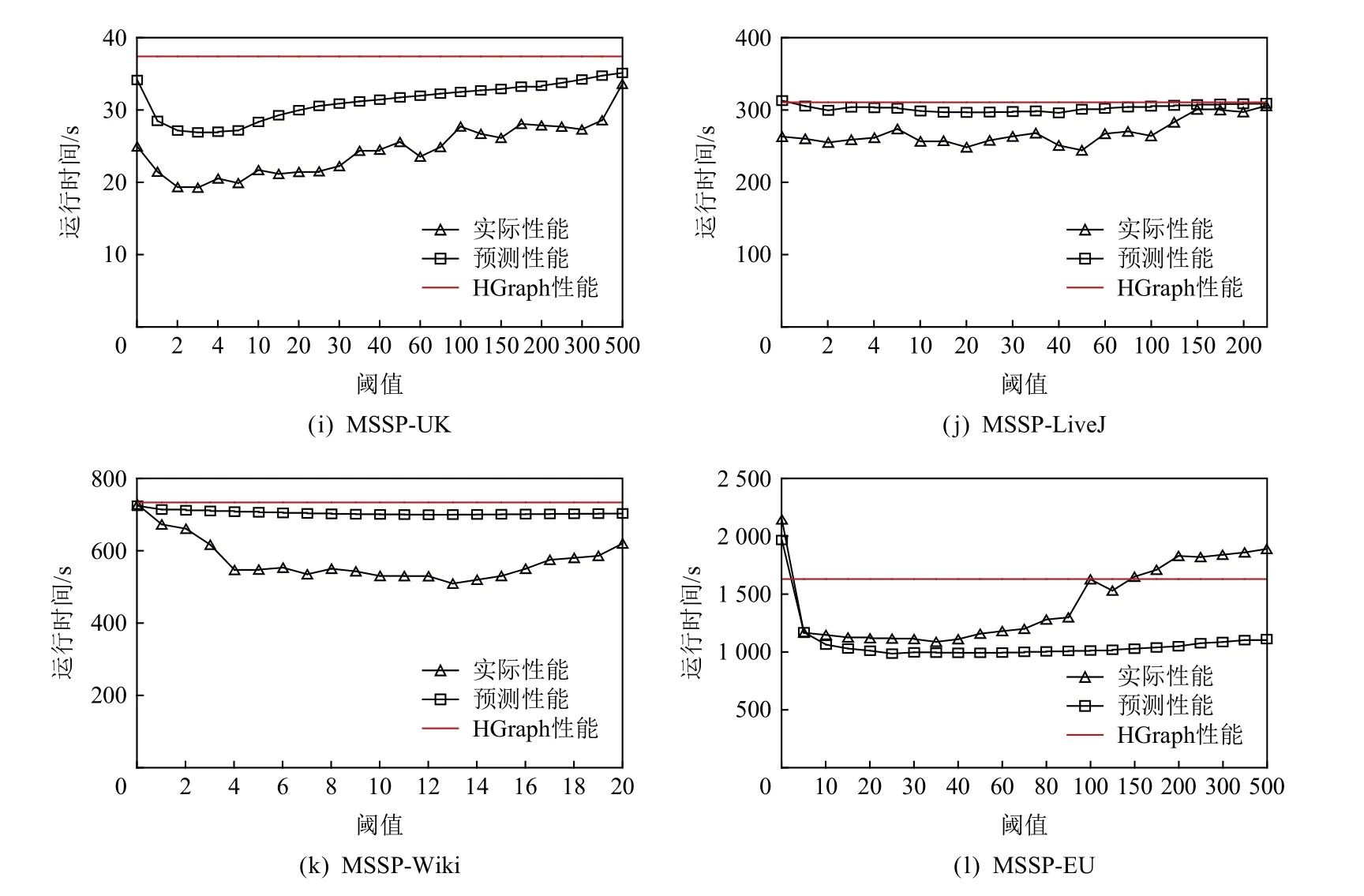
Fig.10 The actual and predicted performance under different replication thresholds圖10 不同備份閾值下的實際和預測性能

需要注意的是，對于整個作業的運行時間問題，SC 與SA 算法均采用10 步迭代計算的時間之和.考慮到頂點備份過程內嵌于數據加載與劃分階段，因此，啟動頂點備份功能后，系統的加載與劃分階段會引入額外的出邊遷移開銷.對比“性能提升”斜杠兩邊的內容可以看到，即使備份機制在加載劃分階段引入了額外遷移開銷，但由于后續迭代過程中產生了巨大的通信收益，前者對綜合性能提升百分比的影響十分微小.以影響最大的Wiki-SA 組合為例，在手工測試的最優閾值下，性能提升比例由53%下降到47.5%,僅產生了5.5%的影響；而在自適應閾值分析模型下，性能提升比例也僅有3%的差距，其綜合性能收益仍然十分可觀.

2）模型開銷.自適應性能優化模型的開銷來源于預測所需參數的獲取，也即算法1 展示的第1 類參數的獲取過程.該過程的核心操作，是在給定的分布式任務數和數據集額外運行一次數據加載，并在加載過程中根據給定的候選閾值數組對不同閾值下的頂點分布以及出邊遷移情況進行參數值統計.圖11 展示了不同閾值粒度（即候選閾值數組長度）下的加載時間開銷.圖12～14 對應列出了3 種不同算法在不同粒度下閾值選擇的準確率.令 θs為模型選擇的最優閾值，而 θ*為表7 中匯報的、通過多次手工調試所得的最優閾值.選擇準確性的計算方式為 |θs-θ*|/θ*.結果顯示，輸入閾值數組的粒度與自適應性能優化模型的統計開銷成反比，與最優閾值選擇的準確性成正比.閾值粒度越細化，解析的參數越多，優化模型對最優閾值的預測結果越精細，利于找到最優閾值；反之，最優閾值的選擇偏差增大，但參數統計操作減少，加載延遲降低.

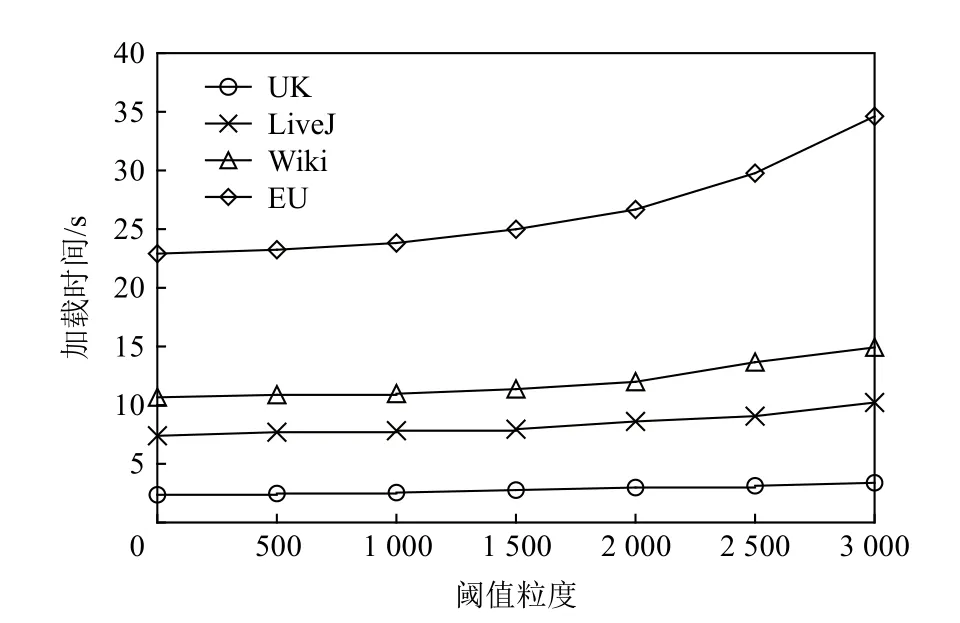
Fig.11 Latency analysis of loading data under different threshold granularities圖11 不同閾值粒度下的數據加載延遲分析

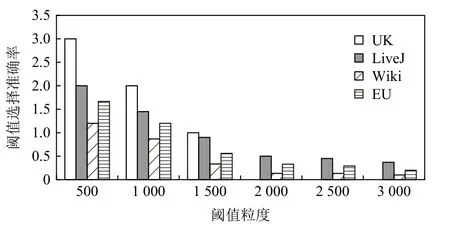
Fig.12 Accuracy analysis of selecting the optimal threshold under different threshold granularities for SC圖12 SC 在不同閾值粒度下的最優閾值選擇準確率分析

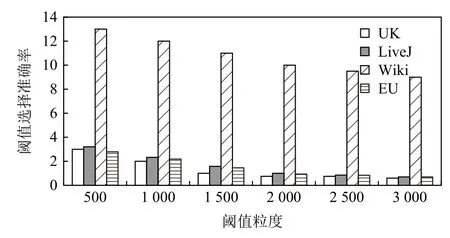
Fig.13 Accuracy analysis of selecting the optimal threshold under different threshold granularities for SA圖13 SA 在不同閾值粒度下的最優閾值選擇準確率分析

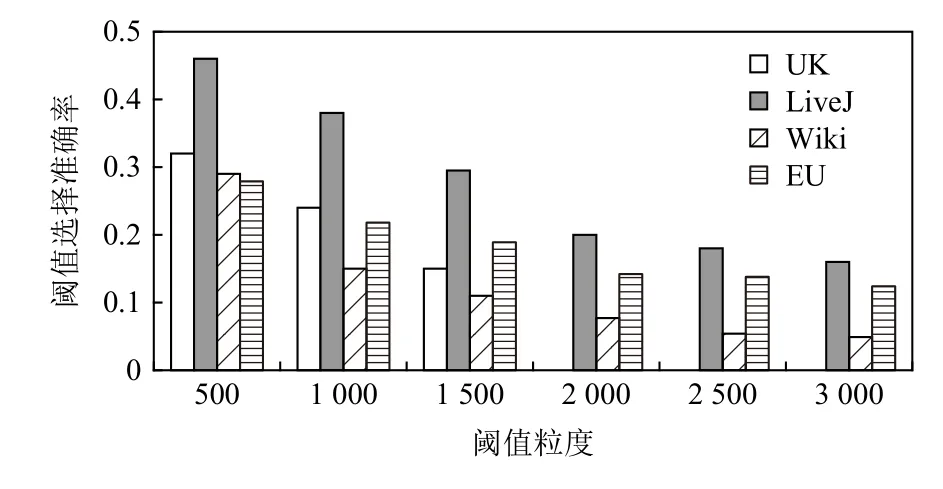
Fig.14 Accuracy analysis of selecting the optimal threshold under different threshold granularities for MSSP圖14 MSSP 在不同閾值粒度下的最優閾值選擇準確率分析

綜合考慮加載延遲和選擇準確性，本文以2000為閾值運行優化模型，以1.12～1.64 倍的延遲獲得較高的選擇準確率.此外，考慮到同一個數據集上的不同應用作業可共享參數統計結果，故該加載過程可視為離線操作，其開銷不計入實時的作業處理時間.

6 結論

通信開銷一直是制約分布式圖處理性能提升的關鍵因素.本文從內存和迭代性能上對現有HGraph系統進行了改進.具體地，本文首先對圖算法進行分類，指出多維消息類算法對通信和內存的緊迫性要求，并以此為基礎在徹底合并系統上引入輕量級頂點備份框架，對系統的內存開銷進行優化.其次，提出了自適應性能優化模型，對頂點參與備份或合并進行定量分析，并對出邊偏移閾值進行優化.大量真實數據集的實驗結果表明，輕量級頂點備份框架在內存和執行時間方面，均優于目前最新的處理平臺HGraph，自適應性能優化模型對最優備份閾值的選擇也表現出很好的適應性.

作者貢獻聲明：杜玉潔參與算法構思并負責完成實驗方案與論文初稿撰寫；王志剛提出了完整的算法框架并修改完成論文終稿；王寧參與了論文的審閱與格式校正；劉芯亦協助完成了相關工作調研與實驗數據整理；衣軍成完成了實驗數據集的收集與格式變換；聶婕與魏志強對論文內容的邏輯布局進行了指導；谷峪與于戈對備份閾值的計算方式提出了指導意見并協助修改論文.