計及需求響應柔性調(diào)節(jié)的可再生能源優(yōu)化配置

程 杉，張芮嘉，鐘仕凌，薛 飛，左先旺

（1.智慧能源技術(shù)湖北省工程研究中心（三峽大學），宜昌 443002；2.國網(wǎng)寧夏電力有限公司電力科學研究院，銀川 750001）

隨著我國的電力需求增長和國家對能源安全、環(huán)境保護的日益重視[1]，構(gòu)建以風力發(fā)電機WG（wind turbine generator）發(fā)電和光伏PV（photovoltaic）發(fā)電等分布式可再生能源DRG（distributed renewable generations）為主體的新型電力系統(tǒng)，具有重大歷史意義和現(xiàn)實意義。但DRG的波動性和不確定性導致的棄電現(xiàn)象使其利用價值不能完全體現(xiàn)，優(yōu)化DRG的配置能提高配電網(wǎng)運行的經(jīng)濟性與可靠性，因此，對含DRG的配電網(wǎng)進行運行優(yōu)化十分必要[2-3]。

為避免或降低DRG出力波動性給配電網(wǎng)帶來的電壓波動[4]和電能質(zhì)量變差等影響[5-6]，隨機優(yōu)化[7]和魯棒優(yōu)化[9]RO（robust optimization）等方法被廣泛應用于解決DRG出力的不確定問題。文獻[7]基于負荷需求和DRG處理的隨機性分布特征差異，提出分類概率綜合多場景分析方法和建立最大化年均收益率、電壓分布改善率的DRG多目標規(guī)劃模型；文獻[8]則考慮主動管理模式，建立基于多場景分析的DRG雙層規(guī)劃模型，上、下層分別以最小化DRG年壽命周期投資成本和最小化DRG有功出力切除量為目標函數(shù)；文獻[9]通過魯棒優(yōu)化消除DRG區(qū)間模型中的不確定變量，采用對偶理論和拉格朗日求導法將主動配電網(wǎng)中DRG優(yōu)化配置的不確定性模型轉(zhuǎn)化為確定性模型后進行求解；而文獻[10]基于Wasserstein概率距離的場景削減0-1規(guī)劃模型對DRG的大量不確定性場景進行削減，建立以最小化投資運行成本為目標函數(shù)的綜合能源系統(tǒng)容量兩階段規(guī)劃方法。

以上研究僅考慮DRG優(yōu)化配置的規(guī)劃模型，沒有充分利用其他配電網(wǎng)資源，這種方法只有在能源互聯(lián)網(wǎng)背景下系統(tǒng)供需雙側(cè)進行資源協(xié)調(diào)互動方可體現(xiàn)用戶參與調(diào)控的響應特征。為此，研究者將單一的DRG優(yōu)化配置問題逐漸擴展為含需求響應DR（demand-side response）的綜合資源規(guī)劃問題，通過激勵用戶改變用電行為以配合DRG出力，并獲得收益的DR策略定義為柔性調(diào)節(jié)[11]。DRG柔性調(diào)節(jié)在減小負荷曲線峰谷差和支撐DRG消納等方面都具有較好效果。文獻[12]將分布式電源、電動汽車、蓄電池和可控負荷定義為廣義DR資源，以經(jīng)濟效益最大化構(gòu)建基于廣義DR資源的微電網(wǎng)綜合資源優(yōu)化規(guī)劃方法，實現(xiàn)柔性響應。具有耦合特性的雙層模型是在配電網(wǎng)優(yōu)化運行的基礎(chǔ)上進行DRG優(yōu)化配置的有效方法，文獻[13]根據(jù)資源出力特性，以最小化投資和運行成本為目標函數(shù)，建立基于機會約束的DRG和DR資源的雙層協(xié)同規(guī)劃模型；文獻[14]利用場景分析方法處理多種DRG的不確定因素，并考慮可控分布式電源和可中斷負荷的調(diào)度運行，建立配電網(wǎng)中DRG的雙層優(yōu)化配置模型。以上雙層模型均未同時計及需求側(cè)柔性調(diào)節(jié)與考慮經(jīng)濟性的規(guī)劃層和可靠性的運行層的耦合運行。合理的電價機制可達到削峰填谷、改善電網(wǎng)負荷曲線的目的[15]，峰、谷分時電價是一種有效的DR機制，通過該機制構(gòu)建綜合考慮經(jīng)濟性與配電網(wǎng)運行穩(wěn)定性的DRG規(guī)劃模型是提高電網(wǎng)運行穩(wěn)定性的有效方式。

本文計及規(guī)劃與運行的耦合特性和能源互聯(lián)網(wǎng)背景下供需雙側(cè)資源協(xié)調(diào)互動的重要特征，建立基于峰、谷分時電價機制和多場景分析法的主動配電網(wǎng)DRG雙層優(yōu)化配置模型，并采用多策略融合粒子群優(yōu)化算法MSPSO（particle swarm optimization algorithm integrated with multiple strategies）對該模型進行求解計算。首先，針對DRG不確定性問題，利用K-means聚類多場景分析法對DRG和負荷進行典型場景劃分。然后，建立DRG并網(wǎng)雙層優(yōu)化模型，上層模型以配電網(wǎng)綜合費用最小為目標，進行DRG選址定容；下層模型以配電網(wǎng)有功網(wǎng)損最小為目標制定峰、平、谷時段售電電價，并采用考慮無功的擬直流潮流模型對潮流方程進行電壓幅值和相角解耦處理。最后，通過IEEE 33節(jié)點配網(wǎng)系統(tǒng)驗證本文所提模型的合理性與可行性，實驗結(jié)果表明，該模型通過DR可以激勵用戶改變用電行為、降低負荷曲線峰、谷差和提高DRG的滲透率、降低棄電率，以及平衡系統(tǒng)的經(jīng)濟性和安全性。

1 DRG與負荷的不確定性模型

1.1 WG出力特性

文獻[16]通過研究證實服從ω（τ，ε）的Weibull分布與風速v隨機特性近似，其概率密度函數(shù)f（v）和分布函數(shù)F（v）可表示為

式中，τ，ε分別為Weibull分布的形狀和尺度參數(shù)。

WG的實際出力PWG與v的關(guān)系可表示為

1.2 光伏出力特性

忽略遮蔽效應，PV出力PPV可表示為[17]

式中：lx為PV輻照強度；NPV為PV電池組件數(shù)；ηn為第n個PV組件的光電轉(zhuǎn)換效率；Sn為第n個PV組件的面積。

文獻[17]通過研究表明，光照強度在一定時間內(nèi)服從Beta分布，由光能-光電轉(zhuǎn)換特性可將PPV分布通過Beta分布表示，其概率密度函數(shù)可表示為

1.3 負荷不確定性

用電規(guī)律的不確定性來源于居民用電習慣、季節(jié)更替和地區(qū)差異等方面，其一定程度上通過用電負荷變化來體現(xiàn)，經(jīng)大量研究證明，居民用電負荷基本服從正態(tài)分布[18]。有功負荷Pload可表示為

式中：Pload服從N（υp，λp）；υp、分別為數(shù)學期望和方差。通過其固定的負荷功率因數(shù)角ψ可得無功負荷Qload=Ploadtanψ。

1.4 不確定性的多場景表征及場景削減

采用文獻[19]所提多場景分析法模擬PWG、PPV和負荷需求的不確定性，根據(jù)WG、PV和負荷的歷史數(shù)據(jù)建立矩陣Mx，y，即

式中，x、y分別為一年天數(shù)及WG、PV和負荷一天的數(shù)據(jù)量。

由于大規(guī)模場景數(shù)量增加了計算量和模型復雜度，故采用文獻[20]所述的K-means聚類方法來削減場景，該方法具有簡單易行、高效率的特點，并可確保削減后的場景多樣性。

2 峰谷分時電價模型

2.1 峰谷分時電價劃分

峰、谷時段的合理劃分有助于提高分時電價的實施效果[21]。本文通過模糊聚類方法[22]將24 h劃分為峰、平、谷3個時段，負荷曲線最低點和最高點分別判定隸屬于谷時段和峰時段，采用半梯形隸屬度函數(shù)判斷其他點處于峰、谷時段。

劃分峰、平、谷時段后實行的分時電價在原有固定電價C0基礎(chǔ)上進行變化，其電價變化量ΔC可表示為

式中，σh、σm和σl分別為峰、平、谷時段的電價變化幅值。

2.2 電量電價彈性矩陣

用戶用電需求量與電價的關(guān)系可通過用戶對電價的多時段響應體現(xiàn)。固定時間段內(nèi)電量電價互彈性系數(shù)由用電量變化率與相應電價變化率之比表示，即

式中：Et、ΔEt分別為t時段的電量和其變化量；CT、ΔCT分別為T時段的電價和其變化量。t與T分別表示不同的時段，t=T和t≠T時所對應的系數(shù)分別為自彈性系數(shù)與互彈性系數(shù)。

由于Et與Ct的關(guān)系可近似為線性關(guān)系[23]，則自彈性系數(shù)dtt可表示為

式中，at、bt分別為Et與Ct線性關(guān)系式的系數(shù)。

在多時段電價響應中，用戶的總用電量基本保持不變，可將dtT表示為

式中，aT、bT分別為ET與CT線性關(guān)系式的系數(shù)。

電量電價彈性矩陣D可表示為

式中，下標h、m、l分別表示分時電價峰、平、谷時段。

電量變化量矩陣ΔE可表示為

3 計及需求響應的DRG配置模型

建立計及DR的DRG雙層優(yōu)化配置模型，其中，上層以含DRG的配電網(wǎng)綜合費用最小為目標函數(shù)得到DRG的位置和容量；下層基于上層得到的優(yōu)化配置方案，以配電網(wǎng)有功網(wǎng)損最小為目標函數(shù)優(yōu)化分時電價。下層運行模型將求解得到的電價反饋回上層，上層根據(jù)反饋結(jié)果對優(yōu)化變量進行再次優(yōu)化，滿足最大迭代次數(shù)后輸出DRG最終配置結(jié)果。雙層優(yōu)化邏輯關(guān)系如圖1所示。

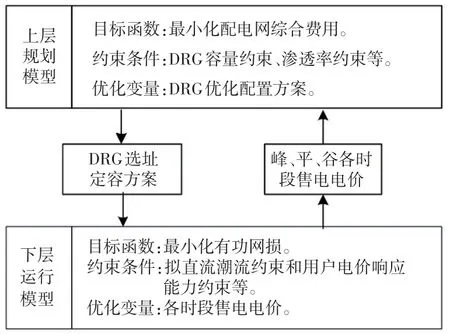
圖1 雙層優(yōu)化模型邏輯關(guān)系Fig.1 Logical relationship in bi-level optimization model

3.1 上層優(yōu)化模型

3.1.1 目標函數(shù)

考慮經(jīng)濟性和環(huán)保性，上層優(yōu)化模型的目標函數(shù)可表示為

式中：Cinv、Com和Cenv分別為DRG的初期投資費用、運維成本和產(chǎn)生的環(huán)境效益；Cpch為配電網(wǎng)向上級電網(wǎng)購電費用。

1）DRG初期投資費用Cinv

式中：Ns為削減后的DRG出力場景數(shù)；Ntp為待規(guī)劃的DRG類型；g=1時表示DRG類型為風機，g=2時為光伏；Ng為安裝的第g類DRG機組數(shù)量；ρr（s）為場景s的概率；為場景s下第g類第z組DRG于節(jié)點i處的并網(wǎng)容量；Z（g）為第g類DRG待選節(jié)點集合；為安裝第g類DRG的單位成本。

2）DRG運行與維護費用Com

3）配電網(wǎng)購電費用Cpch

4）安裝DRG后產(chǎn)生的環(huán)境收益Cenv

3.1.2 約束條件

1）DRG容量約束

2）DRG滲透率約束

3.2 下層優(yōu)化模型

3.2.1 目標函數(shù)

下層優(yōu)化目標函數(shù)可表達式為

式中：Ploss，t為t時段內(nèi)配電網(wǎng)的有功網(wǎng)損；Rij為支路ij的電阻；Ω為支路ij電阻的集合；Pij，t，s、Qij，t，s和Uj，t，s分別為場景s下t時段內(nèi)支路ij的有功功率、無功功率和末端電壓。

3.2.2 約束條件

1）潮流約束

常規(guī)潮流方程可表示為

式中：Ui，t，s、Uj，t，s分別為支路ij的首端和末端電壓；Pi，t，s、Qi，t，s分別為節(jié)點i注入的有功和無功功率；Gij、Bij分別為支路ij導納的實部和虛部；θij，t，s為節(jié)點i、j電壓相角差。

潮流計算通常采用交流模型，屬于典型非線性模型，其求解效率隨系統(tǒng)規(guī)模增大而降低，計算難度也隨之增大。根據(jù)文獻[24]所述方法，將式（21）改寫為

式中，|Yij|、δij分別為Yij的幅值和幅角。

做如下假設(shè)：

式中，λ1、λ2為減少估計誤差的常系數(shù)，基于大量仿真數(shù)據(jù)統(tǒng)計λ1、λ2取值均為0.95。

根據(jù)式（23）～（25），式（22）可表示為

2）節(jié)點電壓約束

3）支路電流約束

式中，Iij，t，s、分別為場景s下支路ij的電流與允許通過電流上限。

4）用戶電價響應能力約束

為保證分時電價實施前后不發(fā)生峰、谷錯位和時段性質(zhì)變化，故峰、平、谷時段的電價關(guān)系為

4 DRG優(yōu)化配置雙層模型求解

采用既增強全局開拓能力又兼顧局部搜索能力的MSPSO算法[25]對上下層模型進行求解計算。

4.1 MSPSO算法

MSPSO引入3種策略，分別為三黑洞系統(tǒng)捕獲策略、多維隨機干擾策略和早熟擾動策略。

經(jīng)三黑洞系統(tǒng)捕獲后粒子xm的位置可表示為

式中：tite為當前迭代次數(shù)；gbest、（gbest+xmax）/2和（gbest+xmin）/2為三黑洞的中心；r為黑洞半徑；r3為[-1，1]的隨機數(shù)；xmax、xmin分別為粒子搜索區(qū)域的上限和下限；為常數(shù)閾值，為[0，1]的隨機數(shù)。

經(jīng)多維隨機干擾策略更新后xm，d的位置可表示為

式中：vm，d為第m個粒子的第d維速度；φ為干擾程度；pth為常數(shù)閾值，pth∈[0，1]；kran、r4均為隨機數(shù)，kran∈[0，1]、r4∈[-1，1]。

粒子的重置位置可表示為

引入?yún)f(xié)調(diào)因子γ以增強算法在尋優(yōu)前期的全局開拓能力和后期的局部搜索能力，其可表示為

式中，Tite為總迭代次數(shù)

4.2 基于MSPSO的雙層模型求解計算流程

基于MSPSO的雙層模型求解流程如圖2所示。上層模型優(yōu)化計算步驟如下：

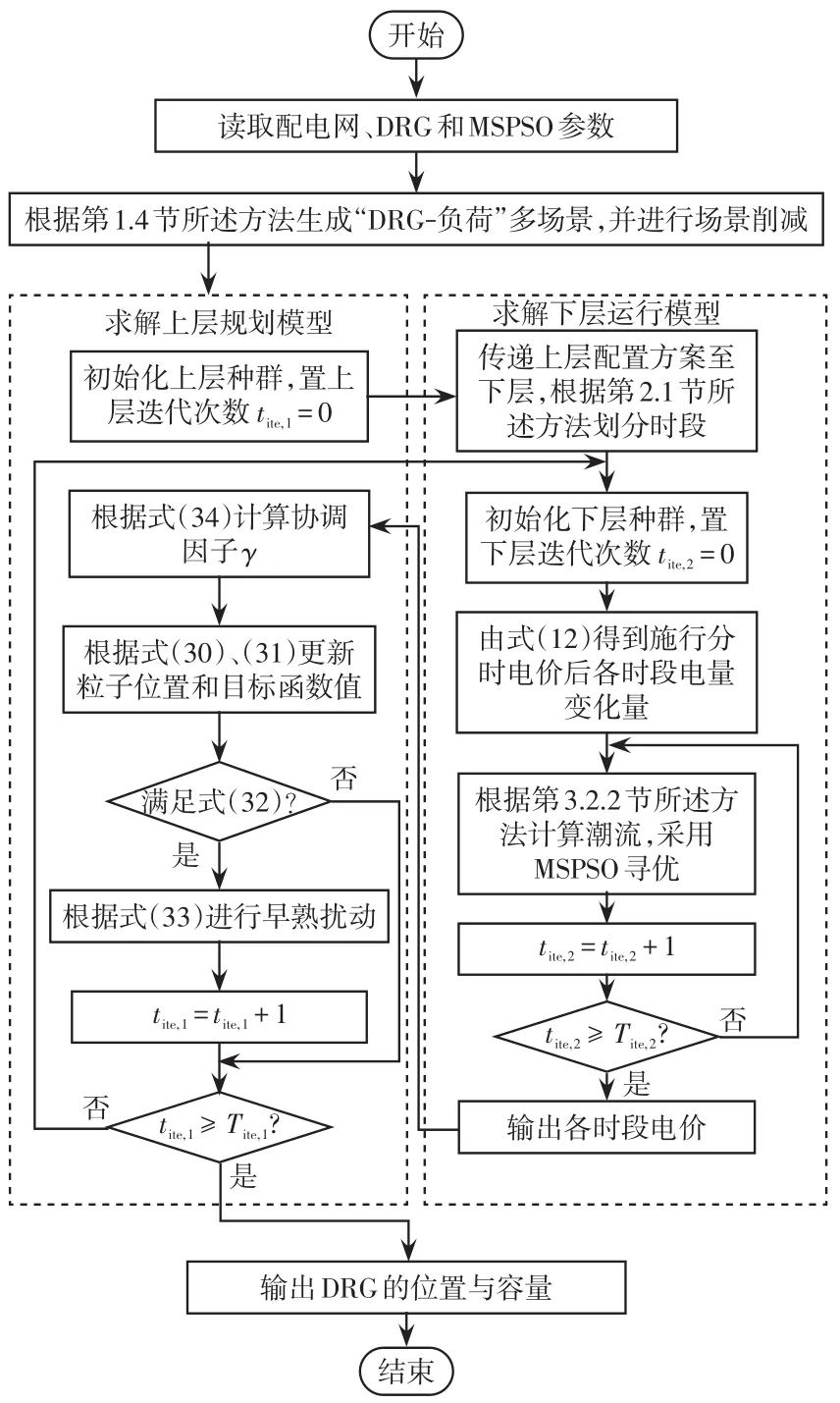
圖2 多策略融合粒子群優(yōu)化算法求解雙層模型流程Fig.2 Flow chart of bi-level model solved by MSPSO

步驟1輸入配電網(wǎng)、DRG和MSPSO算法等參數(shù)；

步驟2建立DRG出力與負荷需求的多場景，使用K-means聚類方法進行多場景削減；

步驟3令上層迭代次數(shù)tite，1=0，初始化上層種群；

步驟4將優(yōu)化配置方案傳遞至下層，下層根據(jù)上層傳遞的方案得到最優(yōu)結(jié)果并送回上層；

步驟5通過式（34）計算協(xié)調(diào)因子γ調(diào)節(jié)全局搜索能力和局部搜索能力，為每一粒子產(chǎn)生隨機數(shù)φ；

步驟6如果γ＞φ，根據(jù)式（30）對粒子進行三黑洞捕獲策略更新；如果γ＜φ，則根據(jù)式（31）進行多維隨機干擾策略更新；

步驟7形成新的粒子位置后，根據(jù)式（32）判斷是否施行早熟擾動策略，若是則按式（33）進行早熟擾動；

步驟8tite，1=tite，1+1。重復步驟4～7，直到上層迭代次數(shù)tite，1≥Tite，1時，輸出最優(yōu)規(guī)劃結(jié)果。

下層模型計算步驟如下：

步驟1根據(jù)第2.1節(jié)模糊聚類方法劃分峰、平、谷時段；

步驟2輸入上層傳遞配置方案，令下層迭代次數(shù)tite，2=0，初始化下層種群；

步驟3通過式（12）計算施行分時電價后負荷需求變化量樣本；

步驟4根據(jù)第3.2.2節(jié)所述擬直流潮流模型進行潮流計算，采取MSPSO對下層種群進行尋優(yōu)，同上層模型計算步驟4～7；

步驟5tite，2=tite，2+1。重復上層模型計算步驟4～7，直到下層迭代次數(shù)tite，2≥Tite，2時，輸出最優(yōu)結(jié)果并送回上層。

5 算例分析

基于IEEE 33節(jié)點系統(tǒng)進行仿真驗證和對比分析。設(shè)節(jié)點電壓允許范圍為0.95～1.05 p.u.，擬在5個節(jié)點安裝DRG，單個節(jié)點DRG最大接入容量為1 000 kW，DRG最大滲透率為70%。風電的候選安裝節(jié)點為5、8、15、16、21、28、31、33；PV的候選安裝節(jié)點為4、7、17、18、24、29、32。WG、PV的單位容量投資成本分別為1.30×103￥/kW和4.55×103￥/kW；風電、PV的維護費用分別為0.10×103￥/kW和0.05×103￥/kW，DRG的環(huán)境效益為0.10￥/（kW·h）。原始負荷曲線及其峰、平、谷時段劃分如圖3所示；IEEE 33節(jié)點配電系統(tǒng)如圖4所示。峰、平、谷時段的具體劃分和3個時段電量電價供給曲線系數(shù)[26]如表1所示；本文采取場景數(shù)=16作為最終場景數(shù)，參考2021年湖北省銷售電價設(shè)定原有固定電價為0.6￥/（kW·h），DRG優(yōu)化配置方案、優(yōu)化電價和綜合費用如表2所示。

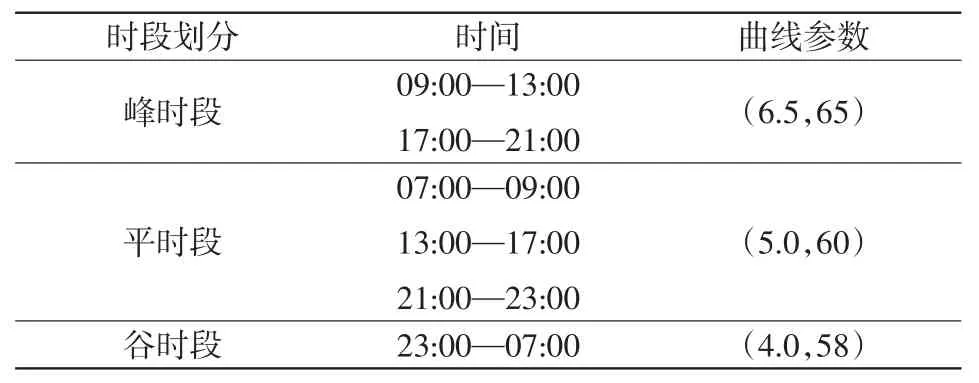
表1 峰平谷時段和電量電價供給曲線系數(shù)Tab.1 Peak，flat and valley periods and the corresponding electricity price supply curve coefficients

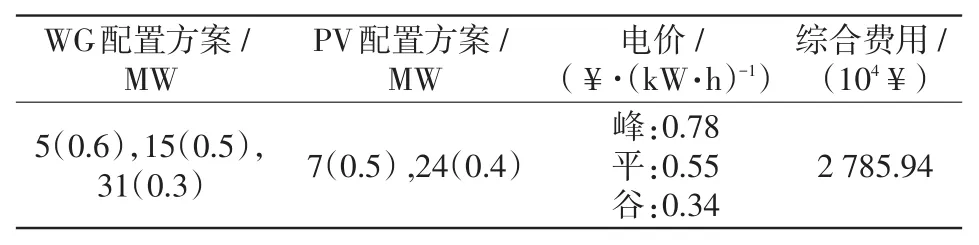
表2 DRG優(yōu)化配置方案Tab.2 Optimal allocation scheme for DRGs

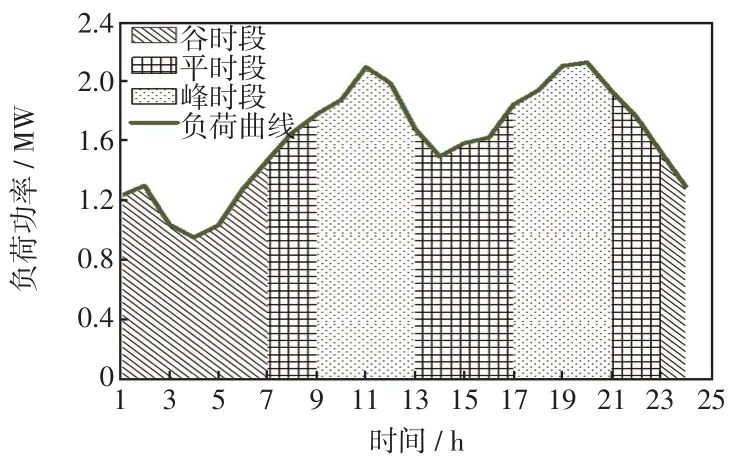
圖3 峰平谷時段的劃分Fig.3 Division of peak，flat and valley periods

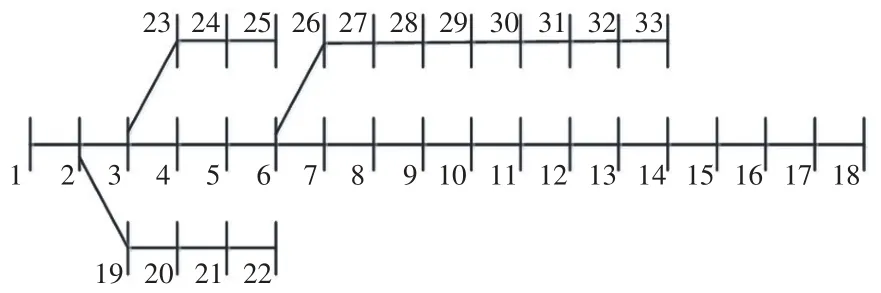
圖4 IEEE 33節(jié)點配電系統(tǒng)Fig.4 IEEE 33-node distribution system

5.1 進行運行優(yōu)化對負荷曲線的影響

系統(tǒng)負荷曲線在施行峰、谷分時電價前后的對比如圖5所示。

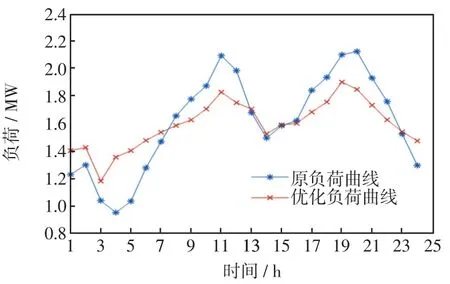
圖5 DR前后的日負荷曲線Fig.5 Daily load curve before and after demand-side response

由圖5可以看出，在進行運行優(yōu)化后，系統(tǒng)負荷的峰、谷差值明顯降低，在不考慮DR時，系統(tǒng)負荷峰、谷差為1 176 kW；在考慮DR后，系統(tǒng)峰、谷差減少為723 kW，系統(tǒng)負荷峰、谷差降低了38.55%。

規(guī)劃-運行雙層模型的下層運行優(yōu)化模型在施行峰、谷分時電價時通過制定峰時高電價、谷時低電價的方式改變負荷曲線的分布，以電價激勵用戶改變用電行為，能降低DRG反調(diào)峰性導致的高棄電率。對于用戶，用電方式的調(diào)整使其在峰時段的用電負荷減少了1 599 kW，谷時段用電負荷增加1 638 kW，規(guī)避高峰期用電，增加平、谷時期用電是降低電費的有效途徑。對于配電網(wǎng)，DR柔性調(diào)節(jié)實現(xiàn)了對負荷曲線的削峰填谷，負荷曲線更加平穩(wěn)，電網(wǎng)可靠性和穩(wěn)定性也得到了顯著提高。

5.2 單層規(guī)劃模型與雙層規(guī)劃-運行模型對比

設(shè)模型1為不考慮運行優(yōu)化的單層規(guī)劃模型，模型2與模型3分別為不計及和計及DR的DRG雙層優(yōu)化配置模型。3種模型的仿真結(jié)果對比如表3所示，其中模型2取固定電價為0.6￥/（kW·h）。

由表3可以看出，模型1的綜合費用最少，但由于僅考慮DRG規(guī)劃的經(jīng)濟性，并未計及配電網(wǎng)優(yōu)化運行，導致其配電網(wǎng)有功網(wǎng)損則比計及運行優(yōu)化的雙層模型高出45%以上；模型2、3均為規(guī)劃-運行雙層模型，兼顧了經(jīng)濟性和運行優(yōu)化，使配電網(wǎng)在運行可靠性得到保障的同時，運行水平也得到提升，故綜合費用略高于模型1；在兩種雙層模型中，模型3采用了峰、谷分時電價，DRG并網(wǎng)總?cè)萘孔畲螅@是因為用戶受到電價的價格變化刺激，使部分峰時負荷轉(zhuǎn)移至平時或谷時，時間上與DRG出力高峰期更加貼近，DRG的利用率得到了提高，并網(wǎng)總?cè)萘吭龃螅浑m然采用固定電價的模型2相較模型3的DRG初期投資費用較少，但其購電需求更高，導致其綜合費用高于模型3。

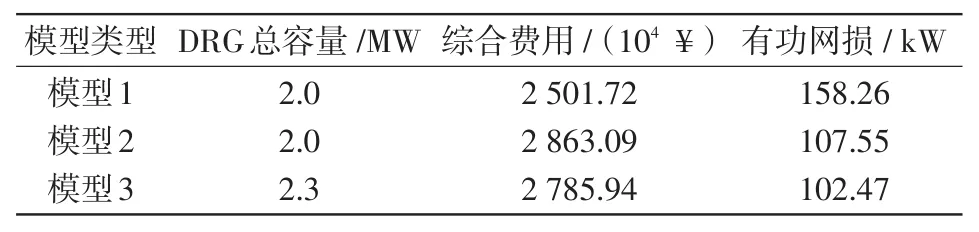
表3 各模型仿真結(jié)果對比Tab.3 Comparison of simulation result among different models

5.3 不同場景數(shù)量對DRG配置方案的影響

本文采取K-means聚類方法進行場景數(shù)削減，分別對8、16、32場景數(shù)下的DRG配置方案和成本分析不同場景數(shù)量對規(guī)劃結(jié)果產(chǎn)生的影響，表4和表5分別為不同場景數(shù)下的DRG配置方案與DRG成本。

表4 不同場景數(shù)下的DRG配置方案Tab.4 Allocation schemes for DRGs with different numbers of scenarios

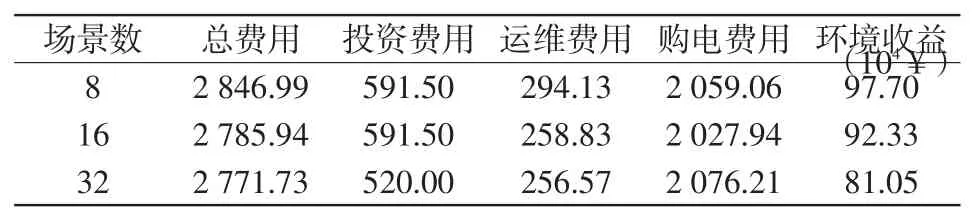
表5 不同場景數(shù)下的DRG成本Tab.5 Costs of DRGs with different numbers of scenarios

由表2、表4和表5可以看出，場景數(shù)為32時，DRG的裝機容量分別比場景數(shù)為8和場景數(shù)為16少300 kW，其綜合費用為3種方案中最少，但購電費用最高。場景數(shù)為8與場景數(shù)為16情況下的DRG裝機容量相同，但場景數(shù)為8情況下的運維費用和購電費用比場景數(shù)為16情況下高出66.42×104￥。場景數(shù)量的增多可以降低DRG的投資和運維費用，但隨著場景數(shù)減少，目標函數(shù)及約束計算難度和計算量也隨之減小，模型求解變得更簡單、更可操作。從不確定性角度考慮，結(jié)果的精確度隨場景數(shù)量而增加，但大規(guī)模場景會使模型變得復雜難以求解。不確定性模型精度與模型計算量之間的矛盾需要通過合理的場景數(shù)量選擇來解決，本文考慮實際配電網(wǎng)規(guī)劃情況，選擇場景數(shù)16作為最終K-means聚類結(jié)果。

5.4 擬直流模型對模型求解的影響

分布式電源接入配電網(wǎng)的規(guī)劃模型實際上是一種典型混合整數(shù)非線性問題，對其進行求解多使用啟發(fā)式智能算法。為探討本文使用的擬直流潮流模型與MSPSO算法對模型求解效率的影響，對傳統(tǒng)潮流-遺傳算法、擬直流-遺傳算法、擬直流-MSPSO 3種模型求解效率和求解精度進行對比，其結(jié)果如表6、表7所示。

表6 模型求解時間對比Tab.6 Comparison of solving time among different models

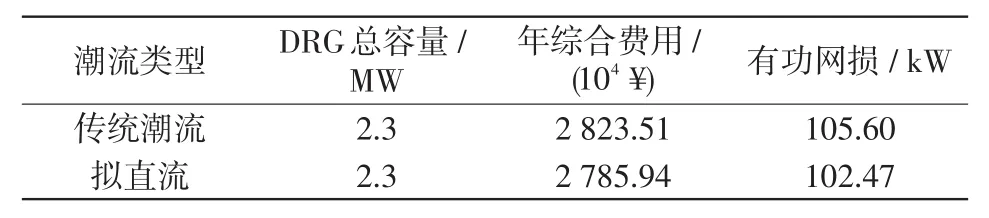
表7 模型求解精度對比Tab.7 Comparison of solution precision between different models

由表6可以看出，采用啟發(fā)式算法對混合整數(shù)非線性問題進行求解有較大難度、耗時較長。采用擬直流潮流模型，相較傳統(tǒng)潮流模型節(jié)約了85.07%的計算時間，計算效率顯著提高。而MSPSO算法利用協(xié)調(diào)因子提高了收斂速度，在擬直流-遺傳算法模型基礎(chǔ)上減少了21.46%的計算時間，在配電網(wǎng)分布式電源規(guī)劃的計算時間方面具有一定優(yōu)勢。

由表7可以看出，傳統(tǒng)潮流模型與擬直流潮流模型規(guī)劃方案相同，優(yōu)化DRG選址定容年綜合費用的誤差率為1.33%，有功網(wǎng)損誤差率為2.96%，擬直流模型引入無功功率的影響，在保證了規(guī)劃結(jié)果精度的基礎(chǔ)上提高了模型求解效率。

6 結(jié)論

本文以擬直流潮流模型為基礎(chǔ)，考慮DRG和負荷不確定性和需求側(cè)電價響應，建立規(guī)劃-運行的DRG選址定容雙層模型。分別以綜合費用最小和有功網(wǎng)損最小為上、下層模型目標函數(shù)，利用MSPSO算法對模型進行求解，得到如下結(jié)論。

（1）K-means聚類削減后的場景數(shù)量增多可以降低DRG的投資和運維成本，但隨著場景數(shù)的減少，模型求解變得更簡單且可操作。因此在實際的配電網(wǎng)規(guī)劃中，應充分考慮實際情況和系統(tǒng)運行的要求。

（2）本文將峰、谷分時電價納入DRG接入配電網(wǎng)的規(guī)劃過程，通過電價型DR柔性調(diào)節(jié)用戶用電習慣，將部分峰時負荷轉(zhuǎn)移至其他時段，使負荷曲線峰、谷差降低，提高配電網(wǎng)的供電可靠性。

（3）本文建立的規(guī)劃-運行雙層模型相較于單層模型能較好地兼顧規(guī)劃目的與系統(tǒng)運行優(yōu)化，平衡了經(jīng)濟性與可靠性，更貼近電網(wǎng)實際運行場景。