一道2021年中考幾何作圖題的解法探究

南京二十九中教育集團初級中學 莊 歷

中學數學教育不僅要讓學生獲得必要的數學知識和技能，還要能讓學生感悟數學的基本思想，積累數學思維活動和實踐活動的經驗.學生解題能力的高低，不僅可以反映其基本知識、基本技能的掌握情況，更可以反映其綜合能力水平.而學生在解題實踐中，常常無法找到解題的入口，不能搭建已知條件和未知結論之間的有效橋梁.因此，教師分析問題時的引導過程就顯得尤為重要，只有從學生的主動思維漸漸推導出所有的可知和需知，找到連接可知和需知之間常用的模型支撐，才能教會學生正確的思考方法，積累探索問題的途徑.本文中以2021年南京市中考中的一道幾何作圖題為例，通過對條件和結論的分析，以及對多種解法的探索，積累基本幾何模型，提高學生的解題能力和綜合分析能力.

1 題目呈現

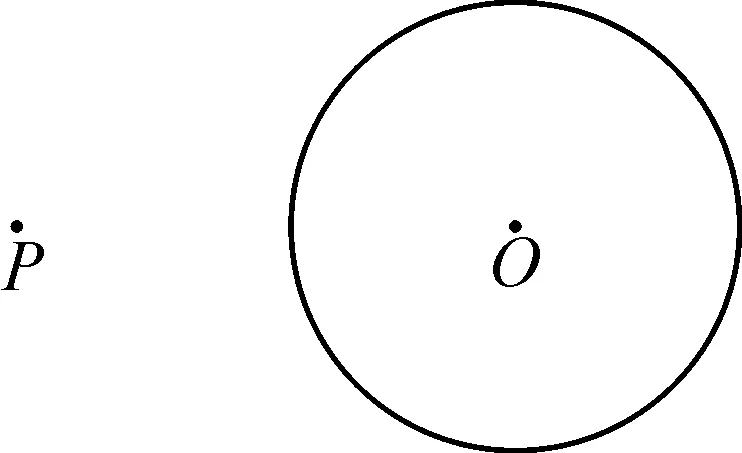
圖1

原題(2021年南京市中考第25題)如圖1，已知P是⊙O外一點，用兩種不同的方法過點P作⊙O的一條切線.要求:(1)用直尺和圓規作圖;(2)保留作圖的痕跡，寫出必要的文字說明.

2 追本溯源

本題是教師和學生都非常熟悉的一道幾何作圖題，在蘇科版九年級上冊“對稱圖形——圓”這一章教授直線與圓的位置關系時，很多教師喜歡用它引入“切線長定理”，但由于新授課教學目標和時間分配的問題，課堂上對于解法沒做過多的探究.新授課時，根據學生的最近發展區，因為他們剛剛學完“圓周角定理”和“直線與圓的位置關系”，所以最容易想到的就是利用“直徑所對的圓周角等于90°”來構造垂直，從而利用“經過半徑外端點并且垂直于這條半徑的直線是圓的切線”證明作法的正確性.

3 解法探究

圖2

首先根據結論畫出目標圖形，理清已知條件和未知結論，探尋它們之間的聯系，找到突破口.要想過點P作⊙O的一條切線，根據切線的判定，如圖2，既可以在⊙O上確定一點A，使得PA⊥OA，即∠PAO=90°，也可過點O向過點P的某直線作垂線，使垂線段的長等于⊙O的半徑.

3.1 “90°角的構造”，探究多種方法

利用切線的第一種判定方法時，對于構造直角，學生并不陌生，在中考復習階段，教師完全可以引導學生找到多個思考角度：

①直徑所對的圓周角等于90°；

②“直角三角形斜邊上的中線等于斜邊一半”的逆命題；

③等腰三角形的“三線合一”；

④矩形的每個內角為直角；

⑤菱形的對角線互相垂直平分；

⑥全等三角形對應角相等.

切入點1：利用“直徑所對的圓周角等于90°”.

作法一：(1)作PO的垂直平分線交PO于點B；

(2)以B為圓心，BO為半徑作⊙B交⊙O于點A；

(3)連接PA，則直線PA即為所求切線，如圖3.

圖4

切入點2：利用“直角三角形斜邊上的中線等于斜邊一半”的逆命題.

作法二：同作法一，如圖4.

理由簡述：因為BP=BA，BA=BO，

所以∠BPA=∠BAP,∠BAO=∠BOA.

又在△APO中，

∠BPA+∠BAP+∠BAO+∠BOA=180°.

所以∠PAO=∠PAB+∠BAO=90°.

切入點3：利用“矩形的每個內角為直角”.

作法三：(1)作PO的垂直平分線交PO于點B;

(2)以B為圓心，BO為半徑作⊙B交⊙O于點A，交AB的延長線于點C;

圖5

(3)連接PA，則直線PA即為所求切線，如圖5.

理由簡述：∵BP=BO，BC=BA，

∴四邊形APCO為平行四邊形.

又BP+BO=BC+BA，即PO=AC，

∴平行四邊形APCO為矩形.

∴∠PAO=90°.

以上三種作法雖然類似，但是構造的基本模型卻不相同.通過不同的切入點，調動學生對幾何圖形的認知，從而“無中生有”構造出不同的基本模型，最后又神奇地統一為類似的作法，讓學生深入了解幾何模型之間的聯系，對構建學生的圖形與幾何板塊的知識結構有很大的幫助.

切入點4：利用等腰三角形的“三線合一”.

作法四：(1)連接PO并延長，交⊙O于點B，C；

(2)以P為圓心，PO為半徑畫弧，以O為圓心，BC為半徑畫弧，兩弧交于點D；

(3)連接OD交⊙O于點A；

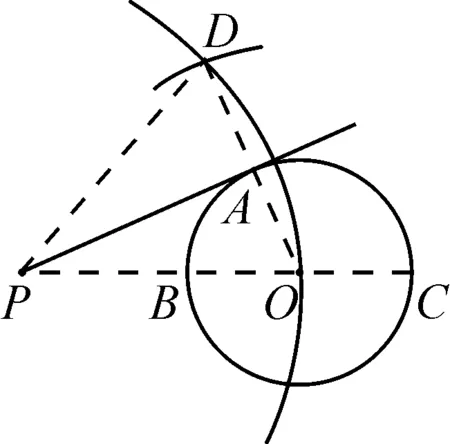
圖6

(4)連接PA，則直線PA即為所求切線，如圖6.

理由簡述：因為PD=PO，DA=AO=r(記⊙O半徑為r)，所以PA⊥DO.

切入點5：利用“菱形的對角線互相垂直，C；

作法五：(1)連接PO并延長，交⊙O于點B，C；

(2)以P為圓心，PO為半徑畫弧，以O為圓心，BC為半徑畫弧，兩弧交于點D，分別以D，O為圓心，PO為半徑畫弧，兩弧交于點E；

圖7

(3)連接PE，DO交于點A，則直線PA即為所求切線，如圖7.

理由簡述：因為PD=PO=OE=DE， 所以四邊形DPOE為菱形.

故OA=AD=r，OA⊥PA.

切入點6：利用“全等三角形對應角相等”.

作法六：(1)在任一直線MN上取點C，過點C作GC⊥MN；

(2)在CG上截取CD=OB；

(3)以D為圓心，PO為半徑畫弧，交MN于點E；

(4)以P為圓心，CE為半徑畫弧，交⊙O于點A，畫直線PA，則直線PA即為所求切線，如圖8.

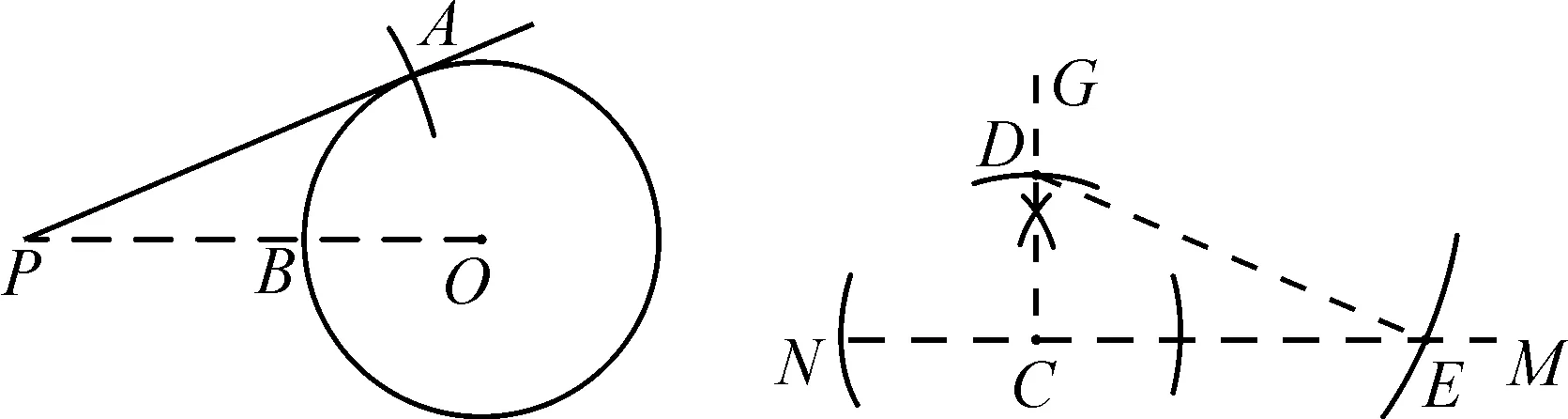
圖8

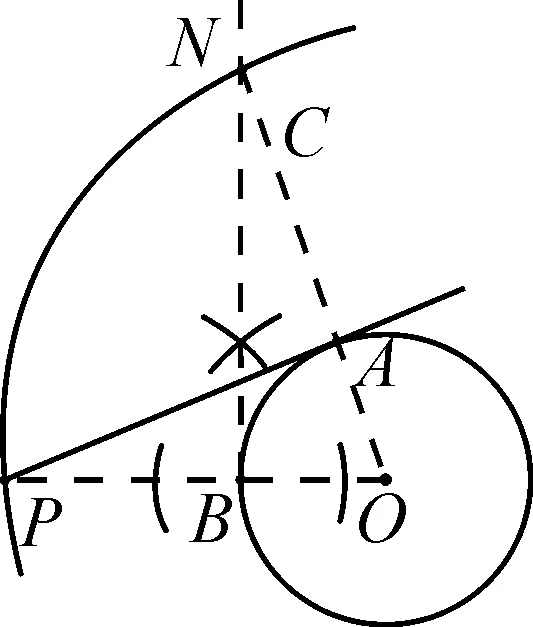
圖9

理由簡述：易證△CDE≌△AOP(SSS).

所以∠PAO=∠ECD= 90°.

對于切入點6，也可以直接在原圖中，借助半徑OB來構造全等三角形，方法類似，如圖9：

3.2 “線段的構造”，探究多種方法

3.2.1 構造半徑OA

除了連半徑，證垂直，同樣可以考慮作垂直，證半徑.對于確定線段OA的長度，可以從以下幾個角度來考慮：①全等三角形對應邊相等； ②相似三角形對應邊成比例.

切入點7：利用“全等三角形對應邊相等”.

圖10

作法七：(1)如圖10，以O為圓心，OP為半徑畫大⊙O；

(2)在小⊙O上任取一點B，連接OB，過點B作OB的垂線，交大⊙O于點C，D；

(3)以P為圓心，CD為半徑畫弧，交大⊙O于點E；

(4)連接PE，過點O作OA⊥PE于點A，則直線PA即為所求切線.

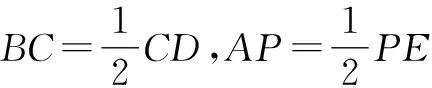
又因為PE=CD，所以BC=AP.

易證△OBC≌△OAP(HL)，則有OA=OB=r.

切入點8：利用“相似三角形對應邊成比例”.

談到相似三角形，大家最容易想到的是“A”字型，我們可以構造一個相似比為1∶2的“A”字模型.

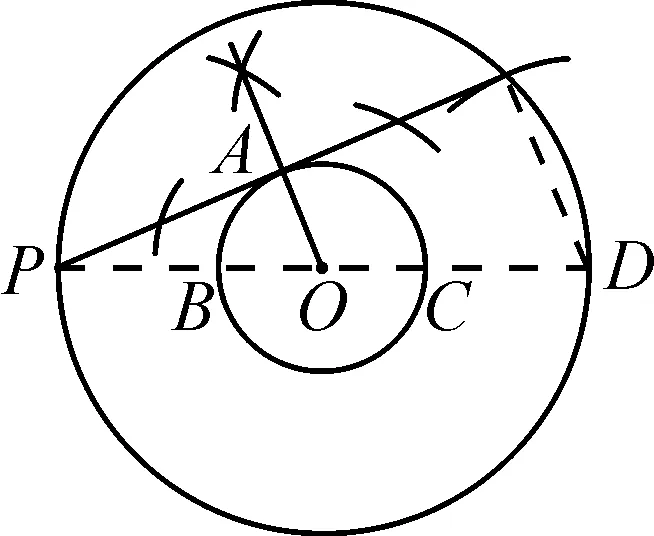
圖11

作法八：(1)如圖11， 以O為圓心，OP為半徑畫大⊙O；

(2)連接PO并延長，交小⊙O于點B，C，交大⊙O于點D；

(3)以D為圓心，BC為半徑畫弧，交大⊙O于點E；

(4)連接PE，過點O作OA⊥PE于點A，則直線PA即為所求切線.

理由簡述：∵PD為大⊙O的直徑，且OA⊥PE，

∴∠PAO=∠PED=90°，則OA∥DE.

∴△PAO∽△PED.

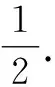
圖12

作法九：(1)如圖12， 作PO的垂直平分線交PO于點C；

(2)作PC的垂直平分線交PC于點D，以D為圓心，PD為半徑畫⊙D；

(3)作BO的垂直平分線交BO于點E，以C為圓心，OE為半徑畫弧交⊙D于點F；

(4)畫直線PF，過點O作OA⊥PF于點A，則直線PA即為所求切線.

理由簡述：∵PC為⊙D的直徑，且OA⊥PF，

∴∠PFC=∠PAO=90°.

即FC∥OA.

∴△PAO∽△PFC.

∴OA=2FC=r.

作法九的思路雖然和作法八類似，都是構造“A”字型從而完成90°的轉化，但是作法九明顯要比作法八復雜.

3.2.2 構造線段PA

不管是連半徑，證垂直，還是作垂直，證半徑，都可以完全確定直角三角形PAO，除了通過確定∠PAO或者OA來完全確定直角三角形PAO，還可以嘗試確定PA的長度.

切入點9：利用“相似三角形對應邊成比例”.

如圖13，我們知道△PAC∽△PBA，從而可以得到PA2=PB·PC，這里PB和PC都是定值，如何確定PA的長度？這一等式讓我們聯想起了“射影定理”.如圖14，在直角三角形EPC中，有PE2=PB·PC，也有EB2=PB·BC.那么，我們只需借助PB和PC構造“母子三角形”，即可確定PA的長度.

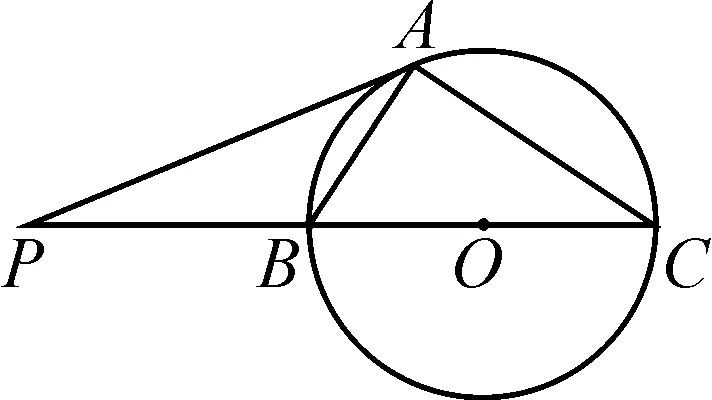
圖13

圖14

作法十：(1)如圖15，連接PO并延長，交⊙O于點B，C；

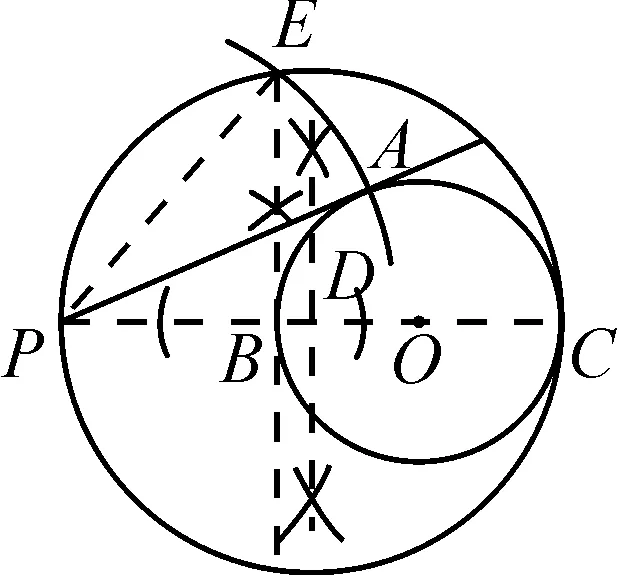
圖15

(2)作PC的垂直平分線交PC于點D；

(3)以D為圓心，PD為半徑畫⊙D；

(4)過點B作PC的垂線交⊙D于點E；

(5)以P為圓心，PE為半徑畫弧交⊙O于點A；

(6)畫直線PA，則直線PA即為所求切線.

4 反思

尺規作圖是學生在圖形與幾何中要掌握的重要技能，需要學生綜合運用所學知識，多角度思考問題，并借助五種基本尺規作圖，完成整個構圖過程.這不僅需要學生熟練掌握五種基本尺規作圖，更需要靈活運用初中的幾何模型.

本題解法很多，但細細想來，主要還是分兩條主線，那就是切線的兩種判定方法：作半徑，證垂直；作垂直，證半徑.根據這兩條主線，分別喚醒學生已有的幾何模型儲備，建立直角模型的構造體系和線段的構造方法.

這道幾何作圖題，可以放在中考一輪復習“圓”這一章，這樣不僅可以幫助學生復習證明切線的兩種方法，更可以激發學生思維的火花，在探尋多種方法的同時，幫助學生復習構造直角和線段的多種方法，讓學生對幾何圖形中基本元素的構造有更多的認識.