捕捉追問時機，提高課堂效率

江蘇省無錫市宜興范道中學 邵亦芬

追問是指針對某一內容追根究底地多次發問.有效的追問可啟發學生的思維，幫助學生形成良好的問題意識，達到答疑解惑的目的[1].數學教學中的追問，一般有順著學生思維與逆著學生思維兩種情況.順向追問一般是學生的回答不夠深刻或比較片面，教師具有導向性的追問，讓學生能深入思考，達到準確與深刻的地步；逆向追問則是在學生回答正確的基礎上，反過來問學生答案的由來，以暴露學生的思維過程.

順向追問更適合用于新知識點的教學，讓學生在抽絲剝繭中逐漸認識到所學內容的本質與內涵；而逆向追問則適用于串聯零散、碎片化的知識點，讓學生在逆向問題的分析與解決中將零碎的知識編織成一張大網，讓雜亂無章的內容變得更加系統化.鑒于此，筆者從自身的執教經驗出發，淺談數學課堂中的有效追問對學生數學思維的形成與發展的影響.

1 追問于思考不夠深刻時

課堂中，常發現有一部分學生的思維會被教師或教材牽著走，從而出現沉默不語、懶得思考的現象.此時，有效追問，具有提神醒腦之功效.在學生思考積極性不高或對問題思考不夠深刻的情況下，有效追問能立即刺激學生的神經細胞，讓他們打起精神進行思考.同時，在問題的逐個解決中，學生體驗到思考帶來的愉悅感，從而對知識產生探究欲.

案例1“平行四邊形”的教學

本章節的內容與其他幾種圖形(矩形、正方形、菱形等)的知識點具有異同點，不少學生學著學著就迷糊了，但又懶得去思考，總是處于一知半解的狀態.為了激發學生的興趣，讓學生徹底搞清楚這些類似圖形的性質，筆者特意設置了以下追問，以幫助學生更好地建構新知.

追問：(1)如何判定一個四邊形是平行四邊形？

(2)若在平行四邊形基礎上添加條件使之成為新圖形，則你想增加什么條件？原圖形變成怎樣的新圖形？

(3)若在菱形或矩形基礎上增減一個條件，則你想增減什么條件？原圖形會發生怎樣的變化？

追問意圖：這幾種相似的四邊形性質有著千絲萬縷的聯系，若逐個加以分析，學生雖然能說出來，但并不能明確這些圖形之間具有怎樣縱橫交錯的聯系.三個追問的提出，不論回答哪個問題，首先，要清楚每種圖形的性質，并在問題的思考與分析中對幾種圖形之間的關系產生了深刻的認識.此過程，在學生夯實基礎的前提下，有效地激活了學生思維的靈活度，讓學生對這幾種圖形的性質產生了更為深刻的理解，對本章節教學起到了顯著的促進作用.

當學生思維處于疲軟期時，有效追問可快速刺激學生的神經細胞，激發學生的思維意識，讓學生進入深度思考狀態，達到解決問題并建構新知的目的[2].因此，教師應時刻關注學生的課堂狀態，選擇在合適的時機給予合適、合理的問題刺激，這對提升課堂教學效率具有明顯效果.

2 追問于學生思維的發散點

有效追問并非隨意提出問題，而是在合適的時機有針對性地拋出一個接一個的問題.追問內容需與前一個問題有一定的相關性，常指向學生的思維發散點，讓學生能從不同角度去觀察與分析問題，在“橫看成嶺側成峰”中達到知其然、知其所以然的目的.至于思維發散點的把握，需教師關注課堂與學生的狀態.有價值的追問，方能凸顯出問題的有效性.因此，何時、何處、如何問值得我們思考.

案例2“平方差公式”的教學

圖1

如圖1，小明從一張大正方形的紙張邊上剪掉了一個小正方形，大、小正方形的邊長分別為a，b.

問題(1)剩下圖形的面積是多少？

(2)如圖2，若將剩下的圖形剪接成一個長方形，則長方形的長與寬分別為多少？面積又是多少？

圖2

(3)通過前面兩問的分析與比較，是否能驗證出平方差公式？

本問題難度較小，但只要親手操作一下，即能很快找出問題的答案.因此，筆者讓每個學生剪裁一張大正方形紙張，再截下一個小正方形.學生在操作、觀察、比較與探索中拼出待求的長方形，問題在毫無懸念中很快得以解決.

為了讓學生更加深刻地認識平方差公式，并學會從不同角度觀察與思考問題，筆者提出追問：請大家尋找其他拼接方法來驗證平方差公式.

學生在合作交流后，給出以下幾種答案.

生1：如圖3，可拼接成一個梯形，來證明平方差公式.

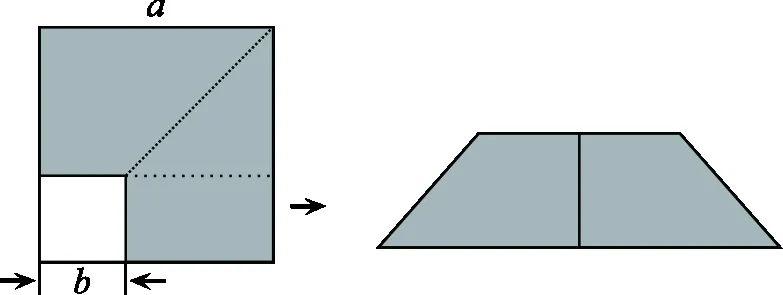
圖3

生2：如圖4，可將剩下的圖形剪開，拼成一個平行四邊形來驗證.

圖4

生3：其實我們都被圖2誤導了，大家都想著用拼圖來計算.事實上，可以將剩下的圖形剪切為兩個一樣大小的直角梯形，通過梯形面積的計算即可得到平方差公式.

師：說說你的計算過程.

師：談談你們此刻的感受.

生4：沒想到平方差公式可以用圖形來驗證，而且有多種方法，數學真是一門神奇的學科.

追問意圖：這種方式擯棄了傳統注入式的教學方法，而是引導學生先動手操作，邊實踐邊思考，每個學生都能從自己習慣的角度去分析與觀察問題，獲得自主解決問題的辦法；同時，受其他同學解題思路的影響，發現除了自身所看到的以外，還有更廣闊的思維空間.這種有效追問的方式，激發了學生自主探究的能力，也有效拓展了學生的思維，讓學生獲得靈活面對各種問題的能力.

3 追問于教學問題的拓展點

教材所呈現的內容是針對大部分學生而設計的，教學時教師需從多個角度去發現與挖掘教材中更為深刻的內容，讓學生形成思維的獨創性.獨創性是一種可貴的數學思維品質，對教學要求比較高.在問題的拓展點實施有效提問，能有效地激發學生產生獨特、新穎的思維[3].

案例3“認識圖形”的例題教學

如圖5所示，△ABC是一塊銳角三角形的鋼板，AD為BC邊上的高.已知BC=120cm，AD=80cm，若想將這塊板加工成一個正方形，使新正方形的一條邊在BC邊上，兩個頂點分別在△ABC的另外兩條邊上，求加工后正方形的邊長.

圖5

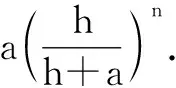
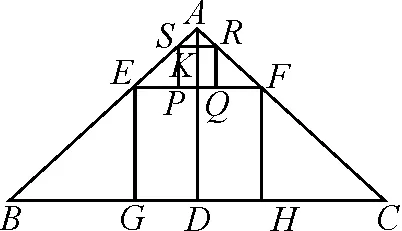
圖6

圖7

追問3：如圖7，在直角三角形ABC內有三個正方形，邊長分別為a，b，c，求證：b=a+c.

追問意圖：逐層遞進的追問，使學生更為深入地理解該部分知識，讓思維具有獨創性.追問1比較簡單，處于學生的認知范圍內，能很快激起學生探究的興趣，因而解決此問沒有障礙.隨著追問難度的加深，學生的思維被徹底開發出來，學生在思維的馳騁中充分發揮各自的創造力，充分體現了思維的深刻性.

總之，問題是課堂教學的靈魂，在減負增效的背景下，高效性體現了教師的智慧與教育的藝術.利用有效追問能啟發學生的思維掀起課堂的小浪花，演繹數學的精彩.因此，有效追問對培養學生的思維能力與數學核心素養具有深遠的影響.