摩擦效應對三維自由彎曲過程中管材變形行為的影響規律研究
于 波,舒 送,程宗輝,,張 浩,程 誠2,,郭訓忠,崔前林
(1.安徽省航空設備測控與逆向工程實驗室,安徽 蕪湖 241007;2.國營蕪湖機械廠,安徽 蕪湖 241007;3.南京航空航天大學 材料科學與技術學院,南京 210016)
1 引言
復雜金屬彎曲管件因具有介質輸運和結構承載等功能,被廣泛應用于航空航天、核能工程、軌道交通以及化工能源等行業[1-2]。常規空間管件彎曲成形方法主要包括壓彎、拉彎、繞彎、推彎、滾彎等傳統彎曲成形技術。但上述方法難以實現復雜軸線彎管構件一次整體成形,常需采用分段近似成形后焊接,容易造成構件軸線精度不高,缺陷形式多樣等問題。三維自由彎曲成形技術通過控制彎曲模的空間運動軌跡,結合管材軸向進給運動,能夠實現三維復雜空間構型彎管一次整體成形[2]。
由于三維自由彎曲過程中管材處于少約束狀態,材料性能以及工藝參數對最終成形管材的形狀尺寸精度以及成形缺陷影響非常顯著。近些年來,相關學者就自由彎曲過程中不同材料類型、彎曲模與管材間隙、內支撐芯棒、管材進給速度等對管材彎曲變形行為的影響規律進行了探索。熊昊[3]通過實驗和理論分析研究了不同材料參數對U-R關系的影響,研究表明相同偏心距下,屈服強度和硬化指數越大彎曲半徑越大;而楊氏模量越大,彎曲半徑越小。郭訓忠等[4]研究了彎曲模與管材間隙及管材進給速度對自由彎曲成形質量的影響,研究表明彎曲模與管材間隙的輕微增加,將導致彎曲半徑的顯著增大,較小的間隙值可降低截面畸變程度,同時研究發現推進速度對壁厚分布與截面畸變的影響并不明顯。程旋等[5]關于不同內支撐材料對自由彎曲成形質量的研究表明,內支撐材料可顯著改善管材內外側壁厚的分布情況,降低截面畸變率,同時內支撐材料分布越均勻,壁厚減薄增厚與截面畸變程度越小。Beulich等[6]通過在管材內部設置內支撐以防止薄壁管在自由彎曲過程中發生軸向失穩等缺陷,并分析了材料模型、內支撐結構以及摩擦條件等對有限元模擬精度的影響。吳建軍等[7]分析了推進速度、周向扭轉速度及彎曲模運動速度對管材彎曲弧段過渡區的影響,并建立了管材彎曲角與穩定區曲率的關系。
此外,三維自由彎曲過程中彎曲模與管材始終處于接觸狀態,彎曲模對管材附加的摩擦效應會影響塑性變形過程中管材內部的應力應變分布狀態,進而影響管材自由彎曲變形行為。目前很少有學者研究自由彎曲過程中摩擦效應對管材成形質量的影響,都是基于傳統彎曲成形工藝分析摩擦因素。Chen等[8]關于不同摩擦形式對彎曲成形的影響表明,滑動摩擦可顯著降低成形力,提高壁厚分布均勻性,降低截面畸變。Yang等[9-10]研究了數控繞彎過程中模具與管材之間的附加摩擦力對彎曲成形質量及成形極限的影響,結果表明增大彎曲模、壓緊模與管材間的摩擦系數可抑制壁厚減薄和截面畸變。吳義旺等[11]通過對大徑厚比小彎曲半徑不銹鋼管進行推彎成形實驗,發現降低內側成形區摩擦力可改善變形區金屬流動,減小彎曲半徑;增大內側引導區與變形區間摩擦系數,可引導材料向變形區流動,減少金屬堆積,降低管材起皺風險。徐竹田等[12]研究發現增加微型板材滾彎成形過程中的摩擦系數,可限制板材的滑動變形,增強材料的拉伸變形量,提高微尺度下板材滾彎成形精度。
在本文中主要研究三維自由彎曲成形過程中摩擦效應對管材成形質量的影響。首先分析了考慮摩擦效應的管材內部應力應變分布情況,揭示處于不同摩擦條件下管材自由彎曲成形機理;其次,基于Cr12MOV材料的彎曲模結構,對比了不同偏心距條件下的彎曲成形實驗與數值模擬結果,驗證了數值模擬方法的可靠性;最后,分析不同摩擦效應對自由彎曲成形過程中管材U-R關系、壁厚分布以及截面畸變的影響規律。
2 考慮摩擦效應的管材自由彎曲成形機理分析
2.1 三維自由彎曲成形原理
三維自由彎曲成形原理圖如圖1所示。自由彎曲成形裝備主要部件包括彎曲模、球面軸承、導向機構和推進機構。在自由彎曲過程中,球面軸承在平面內的水平和垂直運動會帶動彎曲模發生相應平移和旋轉運動,配合推進機構對管材的軸向推進作用,位于導向機構和彎曲模之間的管材發生相應的塑性變形,進而形成彎曲弧段。其中彎曲模中心點與導向機構最前端沿Z軸方向的距離稱為成形區長度A,彎曲模中心點與導向機構最前端在X-Y平面內的投影距離成為偏距U。彎曲過程中,推進機構對管材施加的推進力為PL,彎曲模對管材的成形力為PU,彎曲模對管材的摩擦力為Ff,導向結構對管材的支撐力為PN。在這4種作用力的共同作用下,管材發生彎曲變形,彎矩可以表示為:
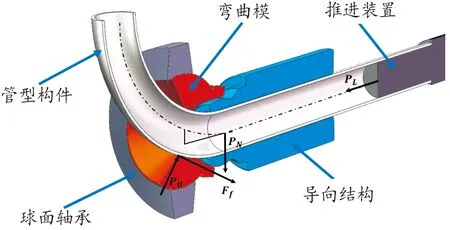
圖1 三維自由彎曲成形原理示意圖Fig.1 Schematic diagram of 3D free bending
M=PNA+PLU
(1)
2.2 考慮摩擦效應的管材應力應變分析
自由彎曲過程中,處于彎曲模和導向機構之間的管材應力應變狀態和幾何參數[13]如圖2所示,其中各符號的含義如表1所示。
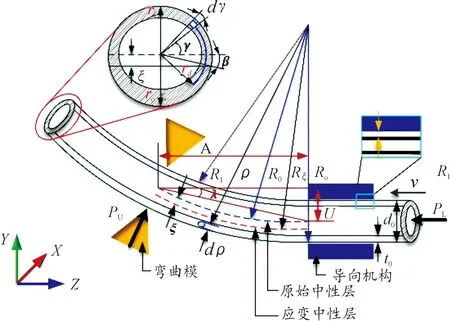
圖2 彎曲段管材應力應變狀態Fig.2 Tube bending stress and strain analysis

表1 管材理論參數對照表Table 1 Comparison of theoretical parameters of tubes
根據Hencky應力應變關系[14],管材徑向方向的力平衡方程可以寫為:
(2)
結合von Mises屈服準則,等效應力可以表示為:
(3)
根據管材環向應變等于0和體積不變假設,管材彎曲圓弧段等效應變可以表示為:
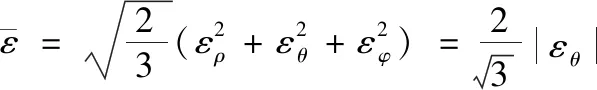
(4)
在軸向推力作用下,自由彎曲過程中應變中性層將會向外偏移,彎曲管材的切向應變為:
(5)
其中,ρ為管材任意位置處沿徑向彎曲半徑。
采用Hollomon方程來擬合管材軸向應力應變曲線:
σ=kεn
(6)
結合式(3)—式(6),可以得到:
(7)
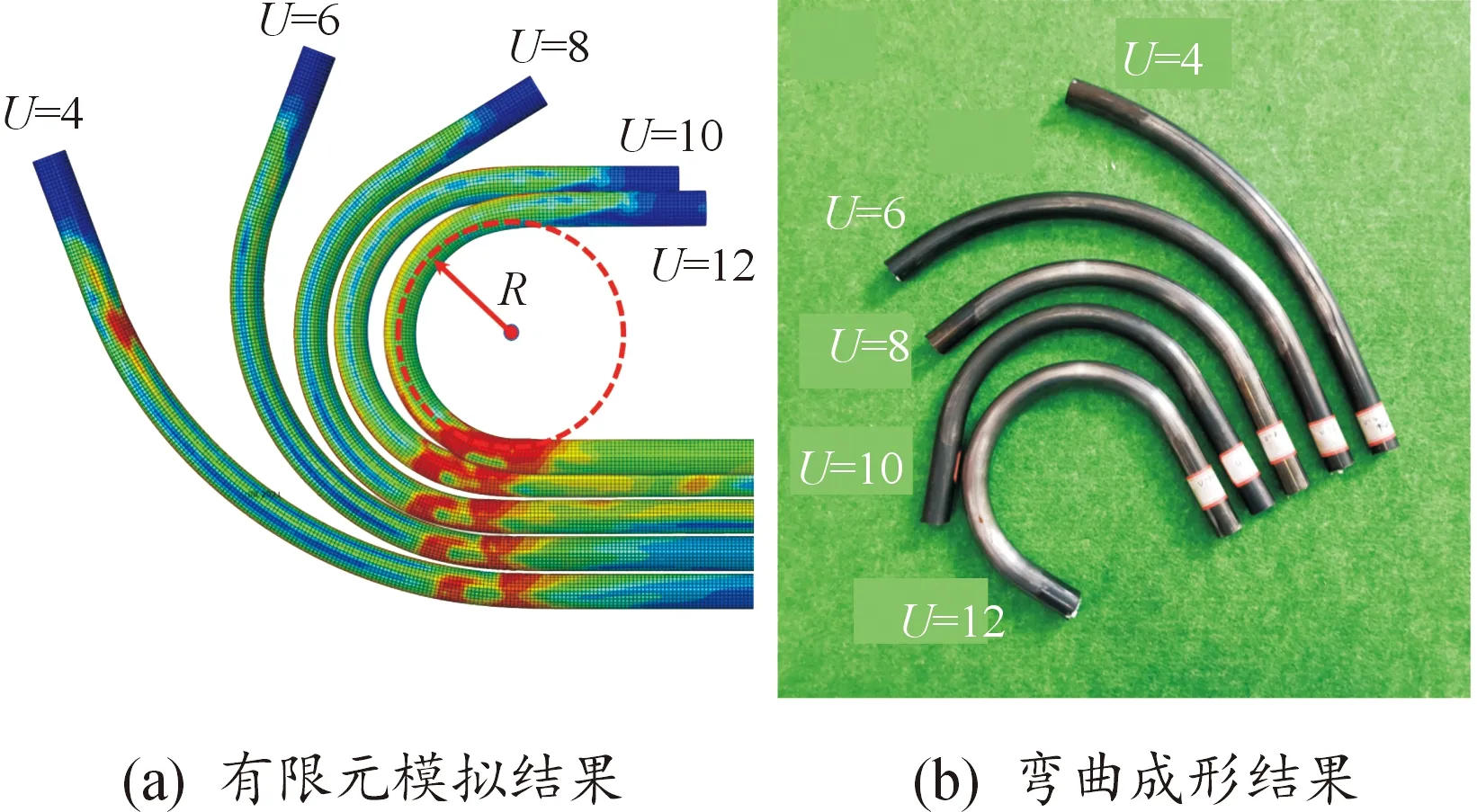
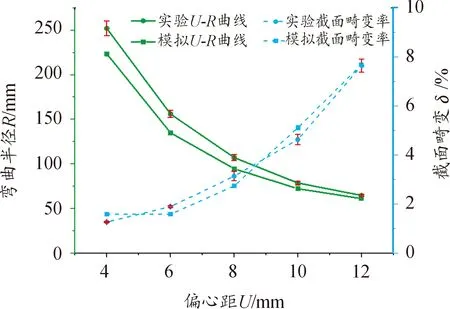
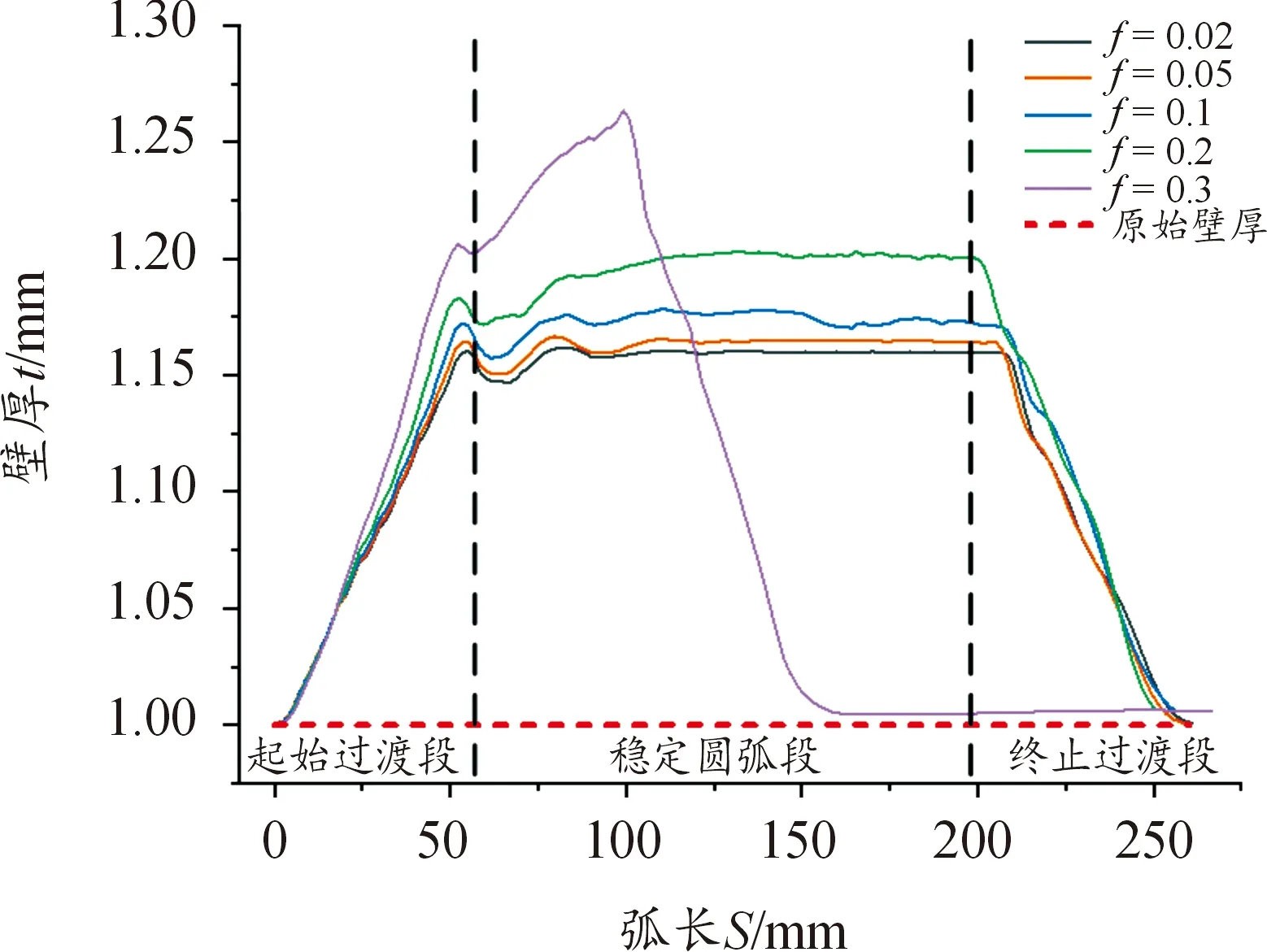
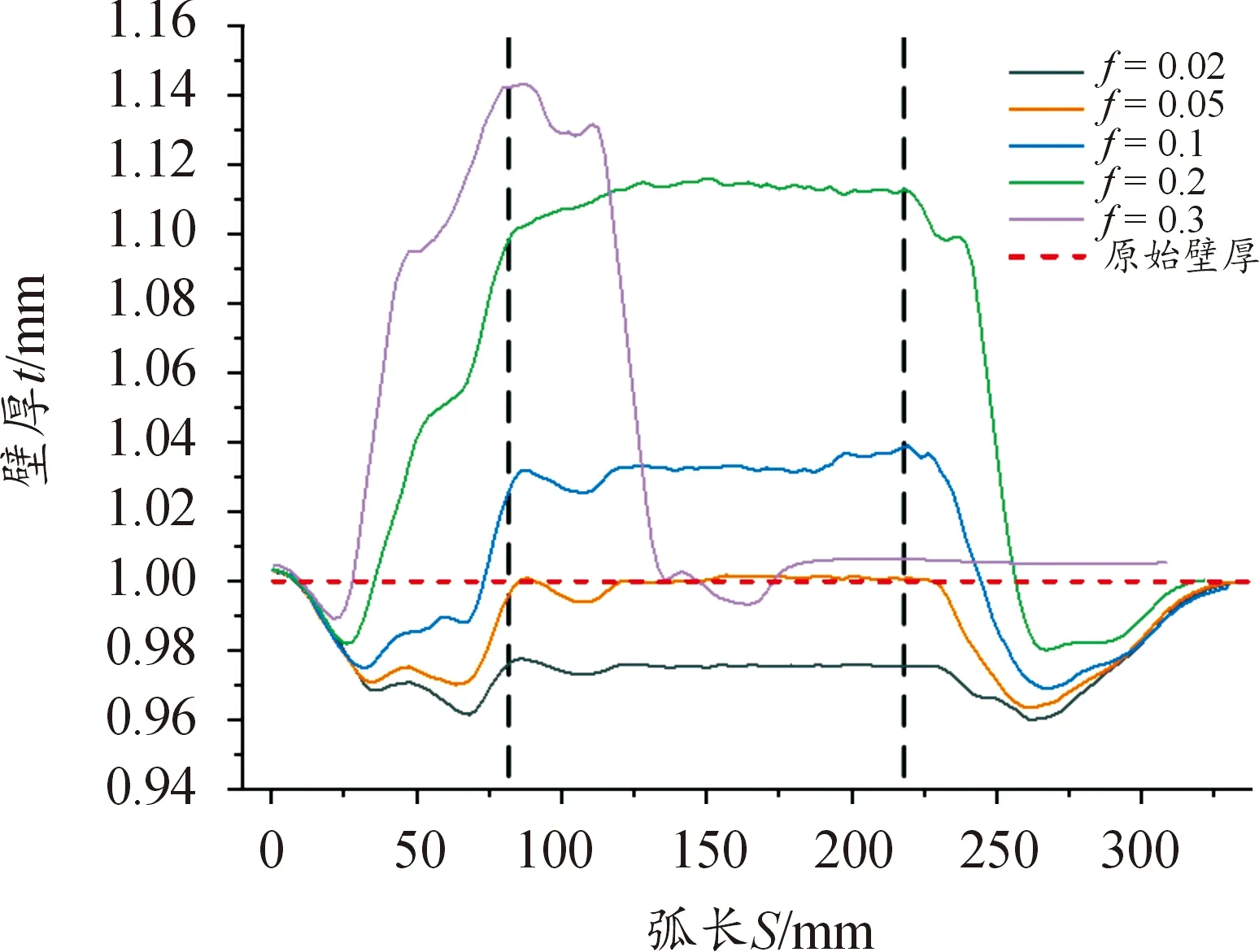
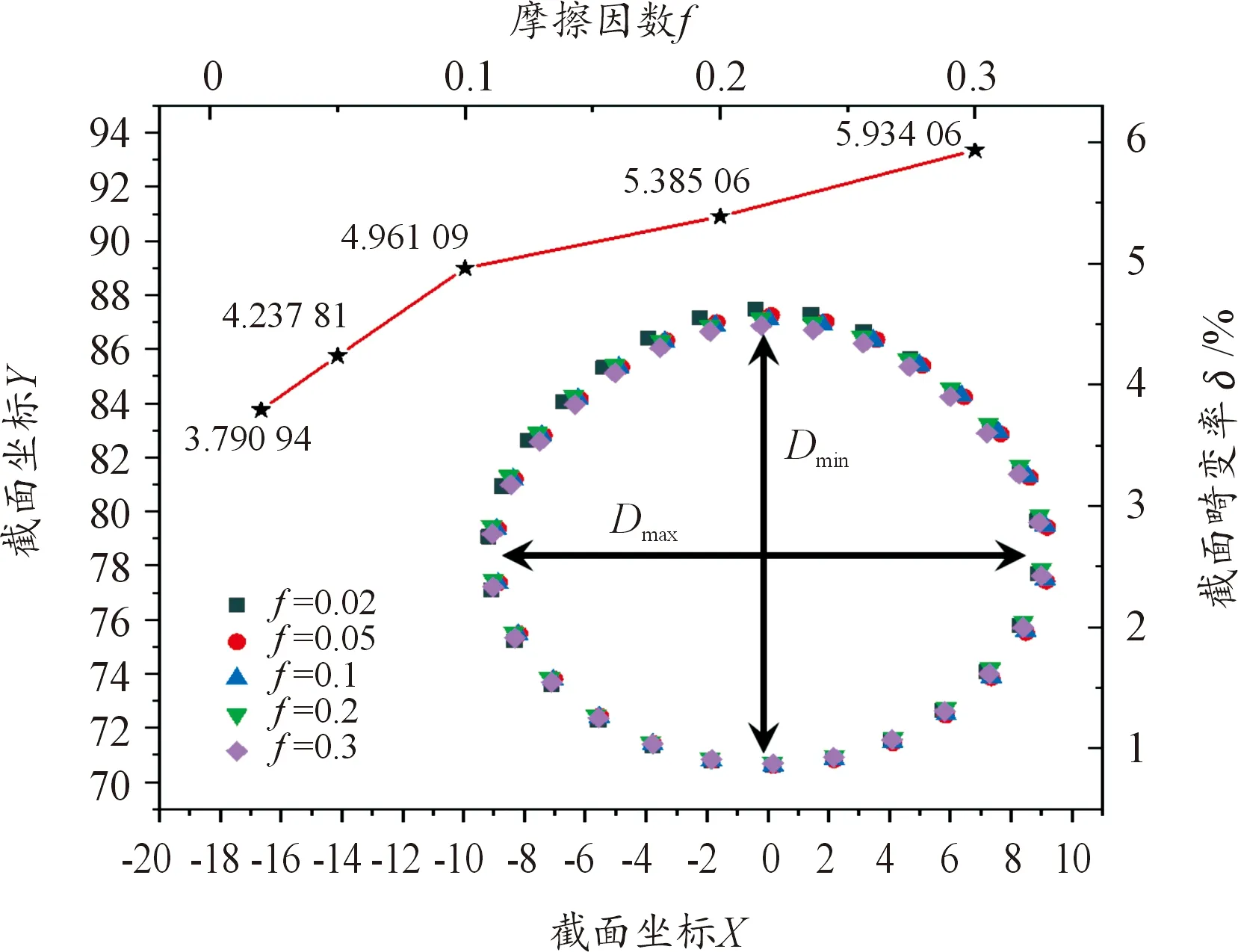
其中,當ρ≥Rξ,管材的彎曲弧段外側處于拉應力狀態,上述公式中“±”取“+”;當ρ 根據式(2)和式(7),可以獲得: (8) 式中,C是常數。由于彎曲弧段最內側和最外側的徑向力等于0,因此彎曲弧段內側和外側的徑向應力和可以推導為: (9) (10) 將式(9)和式(10)代入到式(7)中,彎曲弧段內、外側的切向應力可以表達為: (11) (12) 結合式(9)—式(12)和式(3),管材自由彎曲過程中不同區域等效應力可以確定為: (13) (14) 采用外徑19 mm,壁厚1 mm,經退火處理的20#無縫碳鋼管進行三維自由彎曲成形實驗研究。為了能夠準確模擬碳鋼管自由彎曲過程中的塑性變形行為,需要獲得其基本力學性能參數。根據ASTM standard E8-08標準[15],對金屬管材進行室溫單向拉伸試驗。拉伸試樣沿著管材軸線方向進行截取,圖3所示為縱向弧形拉伸試樣具體幾何尺寸和截取示意圖。經室溫單向拉伸所得縱向弧形拉伸試樣的流動應力應變曲線如圖4所示。 圖3 縱向弧形單向拉伸試樣Fig.3 Longitudinal uniaxial tensile test samples 為了能夠準確描述管材的加工硬化現象,采用Hollomon硬化方程對流動應力應變曲線進行擬合,如式(1)所示。圖4對比了實驗和擬合曲線,從其中可以發現實驗數據與擬合結果高度一致,可以較為真實地反映20#無縫鋼管在彎曲變形過程中的應力應變狀態。根據擬合結果及相關應力應變數據,獲得式(15)本構模型和表2所示20#無縫鋼管力學性能參數。 表2 20#無縫管材力學參數Table 2 Mechanical parameters of the 20# seamless pipe 圖4 碳鋼管材流動應力應變曲線及擬合結果Fig.4 The true stress-strain curve and fitting results of the carbon steel pipe σ=444ε0.074 4 (15) 為研究摩擦效應對管材三維自由彎曲成形U-R關系、壁厚分布及截面畸變的影響,基于管材彎曲有限元仿真軟件,建立20#無縫鋼管三維自由彎曲彈塑性有限元模型。如圖5所示,三維自由彎曲成形有限元模型主要包括彎曲模、球面軸承、導向結構、壓緊裝置以及管材等部件。因在本文中僅研究摩擦因素對管材彎曲成形的影響,為排除無關因素的影響,將除管材以外的所有部件約束為剛性體,其中彎曲模、導向結構和球面軸承定義為剛性實體,壓緊裝置采用剛性殼體,管材采用可變形殼體,并分別對以上部件和管坯進行網格劃分。 圖5 管材三維自由彎曲有限元模型Fig.5 FE modeling of 3D free bending 在本文中主要通過改變管材與彎曲模之間的摩擦系數來研究摩擦效應對管材自由彎曲變形行為的影響。由于實驗所用彎曲模和導向結構的材料均為Cr12MOV,根據WANG[16]和M[17]關于Cr12MoV與碳鋼摩擦之間摩擦磨損的研究結果,確定有限元模擬摩擦系數f=0.2,隨后按照表3所設定工藝參數進行三維自由彎曲有限元模擬成形實驗。 表3 三維自由彎曲有限元模擬實驗工藝參數設置Table 3 Geometrical and setting parameters of the 3D free bending finite element model 為驗證所建立有限元模型的可靠性,基于南京航空航天大學所研發的三維自由彎曲成形工程樣機(見圖6)進行自由彎曲成形實驗。其中彎曲模在球面軸承和導向機構的配合下,將X-Y平面內的平動轉化為圍繞導向機構的旋轉運動,以實現彎曲模空間姿態的變換,Z軸則用以實現管坯的進給運動。X、Y、Z三軸在中央控制器的統一控制下,以一定的匹配速度進行運動,即可實現具有空間結構特征的管材整體彎曲成形。 圖6 三維自由彎曲成形工程樣機Fig.6 3D free bending experimental samples 參照表3,采用與有限元模擬相同的工藝參數進行彎曲成形實驗,圖7分別為有限元模擬和成形實驗所獲得的平面單彎構件。從其中可以初步總結出,有限元模擬方法所獲得的彎曲管材整體形狀尺寸與試驗結果比較接近。圖8對比了實際成形實驗和數值模擬獲得的回彈后彎曲管材U-R關系、不同偏心距下的截面畸變率情況(由式(16)計算)。可以發現,隨著偏心距的逐漸增大,彎曲半徑R呈現減小的趨勢,而截面畸變表現出逐漸上升的趨勢。說明隨著偏心距U的增加,自由彎曲過程中管材的塑性變形程度增加,變形更加劇烈。此外,由實驗和數值模擬方法獲得的U-R關系曲線以及截面畸變變化趨勢基本一致,其中U-R關系最大誤差為11.33%,截面畸變最大誤差為13.56%,表明在本文中所建立的三維自由彎曲有限元模型可以較為準確地預測金屬管材三維自由彎曲塑性變形過程,能夠用于探究摩擦效應對金屬管材彎曲成形質量的影響。 圖7 三維自由彎曲成形結果Fig.7 3D free bending forming results 圖8 U-R關系曲線和截面畸變率對比Fig.8 U-R curves and comparison of section distortion rates (16) 式中:Dmax為管材橫截面最大尺寸;Dmin為管材橫截面最小尺寸;Do為管材橫截面原始直徑,具體測量方式如圖9所示。 圖9 管材截面畸變測量方法Fig.9 Method for measuring cross section distortion of tube 三維自由彎曲成形過程中,管材的U-R關系曲線、壁厚減薄率和截面畸變率是影響管材最終服役性能的關鍵指標參數。彎曲模與管材之間的摩擦效應會改變管材塑性變形段應力應變分布狀態,進而影響已成形管材彎曲半徑、壁厚增厚及減薄和截面畸變。基于所建立的20#薄壁無縫管彈塑性有限元模型,采用0.02、0.05、0.1、0.2、0.3摩擦系數,分別研究摩擦效應對管材彎曲半徑、壁厚增厚減薄和截面畸變的影響規律。 圖10對比了不同摩擦系數條件下U-R關系曲線演化趨勢。從其中可以發現,數值模擬獲得U-R關系曲線明顯高于理論U-R關系曲線。這是由于理論模型下,假設彎曲模和導向機構之間管材為標準圓弧段;而在實際彎曲成形過程中,存在管材彎曲回彈以及圓弧逐漸過渡現象,導致實際圓弧曲率半徑要大于理論計算結果。此外,隨著摩擦系數的升高,不同摩擦系數所對應的U-R關系曲線整體下移。在相同偏心距條件下,摩擦系數越大,可獲得的彎曲圓弧曲率半徑越小。如圖11所示為管材在不同摩擦系數條件下的切向應力分布云圖。 圖10 不同摩擦系數對U-R關系的影響Fig.10 Influence of different friction coefficients on U-R relationships 圖11 不同摩擦系數應力分布云圖Fig.11 Strain cloud diagram with different friction coefficients 由圖11可見,隨著摩擦系數的增加,峰值應力分別向彎曲段內外側轉移,使得切向應力形成的旋轉力矩隨之增加。管材的彎曲變形主要是由切向應力在彎曲平面內所形成的合力矩使管材橫截面圍繞彎曲軸進行剛性旋轉和塑性流動而形成[18],因此在相同的偏心距條件下,摩擦系數越大,所形成的彎曲半徑越小。同時,圖11中管材應力分布由應變中性層向兩側逐漸增加的趨勢,與式(13)、式(14)中對應力分布規律相吻合,進一步證明了有限元模擬結果的可靠性。為了能夠準確獲得自由彎曲過程中管材軸線的尺寸形狀,需要考慮摩擦效應對U-R關系的影響,針對相同曲率半徑圓弧,需根據不同摩擦系數條件對彎曲模偏距U進行調整補償。 圖12為不同摩擦系數下彎曲弧段內凹側壁厚分布情況,結合圖13所示管材應力分布云圖。 圖12 彎曲段內凹側壁厚分布(U=12 mm)Fig.12 Wall thickness distribution of the concave side in a bending section(U=12 mm) 圖13 不同摩擦系數對應壁厚分布云圖Fig.13 Wall thickness cloud diagram with different friction coefficients 不同摩擦系數下的壁厚分布均呈現顯著的三段式演化規律,分別與三維自由彎曲圓弧形成過程中的起始過渡段、穩定圓弧段、終止過渡段相對應。在起始過渡段中,壁厚近似線性增加,達到峰值壁厚后有所降低,并在穩定圓弧段平緩波動,直至終止過渡段快速降至原始壁厚。彎曲圓弧曲率半徑隨弧長的演化情況也被顯示在圖12中。從其中可以發現,彎曲弧段內側壁厚增加區域與圓弧曲率半徑減小區域所對應,說明壁厚增加是由于應變中性層隨彎曲半徑減小向彎曲外側移動所導致的。而壁厚減小弧長區域內彎曲半徑逐漸增大,塑性變形程度越來越小。此外,彎曲弧段內凹側壁厚隨著摩擦系數的增加顯著增厚,且摩擦系數越大,壁厚增厚趨勢越明顯,彎曲內凹側最大壁厚增厚率達到26.5%。由于摩擦力的存在,導致管材內凹側切向壓應力增大,由于管材周向變形受彎曲模具約束,因此管材徑向應變進一步增大以轉移由切向壓縮積累的材料,從而導致彎曲弧段內凹側壁厚進一步增加。 圖14顯示了不同摩擦系數下彎曲弧段外凸側壁厚分布情況。可見,當摩擦系數較小時,彎曲弧段外凸側壁厚小于原始壁厚,管材呈現壁厚減薄現象。隨著摩擦系數的增加,管材穩定圓弧段的壁厚呈現逐漸上升的趨勢,管材外凸側由壁厚減薄向壁厚增厚轉變。這是由于當摩擦系數較小時,彎曲弧段外凸側切向處于拉應力狀態,并產生拉伸變形,為補償切向金屬流失,管材橫截面產生徑向壓縮,從而導致彎曲弧段外側壁厚減薄。隨著摩擦系數的增加,管材進給彎曲過程中所受摩擦阻力增大,導致彎曲弧段外凸側逐漸由拉應力狀態向壓應力狀態轉變,從而出現與彎曲弧段內凹側類似的壁厚增厚現象。 圖14 彎曲段外凸側壁厚分布(U=12 mm)Fig.14 Wall thickness distribution on the convex side of a bending section(U=12 mm) 如圖15所示,為不同摩擦系數條件下,彎曲弧段管材橫截面畸變情況。由圖15可以發現,橫截面畸變隨著摩擦系數的增加逐漸增大,且主要表現為短軸縮短,而長軸的變化并不明顯。管材彎曲時彎曲弧段外凸側直接與彎曲模接觸,在徑向壓應力的作用下迫使外側管壁徑向移動,從而截面在短軸方向縮短較為明顯。隨著摩擦系數的增加,彎曲所需成形力逐漸增大(見圖16),徑向應力隨之變大,導致截面畸變程度不斷增加。圖16中截面畸變率隨著摩擦系數的增加,存在明顯轉折點,當摩擦系數超過0.1后,截面畸變率隨著摩擦系數的增加,上升速度有所降。這是因為當摩擦力超過某一臨界值后,與彎曲模接觸部位,沿管壁周向的摩擦效應開始凸顯,并表現出阻礙金屬周向流動的特征,從而對截面畸變起到一定的抑制作用。 圖15 穩定圓弧段截面畸變情況Fig.15 Section distortion of stable arc section 圖16 彎曲段形成過程中成形力變化Fig.16 The forming force changes during the forming of a bending section 綜上所述,通過理論分析與有限元模擬相結合的方法,探究了三維自由彎曲成形過程中,彎曲模具與管材之間的摩擦系數對管材彎曲半徑、壁厚分布以及截面畸變的影響規律,結果表明摩擦效應對管材三維自由彎曲成形過程中材料塑性變形行為影響顯著: 1) 隨著摩擦系數的增大,材料塑性流動受阻,切向應力幅值升高,彎曲力矩隨之增大,導致在相同的偏心距條件下,管材的彎曲半徑更小。 2) 隨著摩擦系數的增大,彎曲弧段內凹側切向壓應力增大,外凸側切向應力減小,管材彎曲內側壁厚進一步增大,而彎曲外側由壁厚減薄逐漸轉變為壁厚增厚。 3) 隨著摩擦系數的增大,徑向壓應力的增加導致管材橫截面畸變逐漸增大;而摩擦系數的進一步增大又阻礙了管材沿周向流動,從而延緩了截面畸變率上升速率。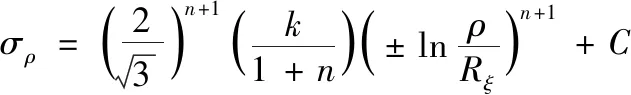
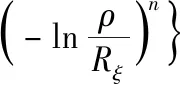

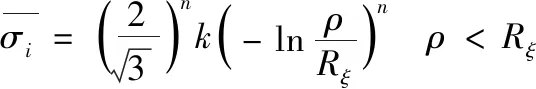
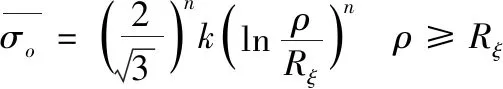
3 三維自由彎曲成形有限元模擬和成形實驗
3.1 單向拉伸實驗



3.2 三維自由彎曲有限元模型建立


3.3 三維自由彎曲實驗

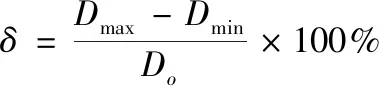

4 結果分析
4.1 摩擦效應對U-R關系的影響


4.2 摩擦效應對壁厚分布的影響

4.3 摩擦效應對管材截面畸變的影響

5 結論

