基于調諧質量阻尼器的摩托車手把減振研究

黃澤好，蔣 歡，童 勇，楊峻懿

(1.重慶理工大學 汽車零部件先進制造技術教育部重點實驗室,重慶 400054；2.重慶理工大學 車輛工程學院,重慶 400054；3.重慶青山工業(yè)有限責任公司,重慶 402761)

1 引言

摩托車手把振動主要由發(fā)動機從不同路徑傳遞至手把疊加而成，而手把振動易導致駕駛員疲勞、麻木，繼而影響駕乘舒適性與安全性[1]。為改善手把振動，Usamah[2]應用橡膠懸置隔離三角臺傳遞至手把桿的振動，并通過試驗驗證了其方案的有效性；汪先國[3]在摩托車手把安裝座中應用橡膠材料，以柔性連接實現(xiàn)手把減振；Mahachai[4]應用多目標優(yōu)化獲得了使手把振動最小的手把結構形狀與尺寸。為進一步改善手把振動，有學者提出在手把管末端引入TMD來控制感興趣頻率范圍內的手把振動。TMD是由輔助質量、彈簧和阻尼組成的被動式吸振器，其小型輕量并能良好的減振效果。Agostoni[5]通過試驗證實TMD能夠抑制手把振動；Khune[6]指出TMD有助于減小高頻手把的振動幅度，減振效果隨著質量的增加而更優(yōu)。以往研究表明了手把TMD減振的有效性，但幾乎沒有給出詳細的手把TMD參數(shù)值的設計方法。在工程實際中，也往往忽視了其減振功能，而充當為手把平衡塊。

本文為減小某摩托車手把振動，對手把調諧質量阻尼器TMD進行研究。根據(jù)手把TMD安裝方式，提出一種嵌入式TMD動力學模型。以手把第一階振動模態(tài)頻率為TMD調諧頻率，以抑制手把振動加速度響應為目標，結合Den Hartog定點理論和等價質量識別法確定嵌入式TMD最優(yōu)減振設計參數(shù)值。通過分析發(fā)動機激勵下的手把振動，證明手把嵌入式TMD的減振優(yōu)越性，為摩托車手把TMD的參數(shù)設計提供參考。

2 手把振動研究模型

2.1 模型建立

使用平均尺寸3 mm的體單元和殼單元對車架、手把、搖臂等結構進行網(wǎng)格劃分；采用seam單元實現(xiàn)不同結構間的焊連接；以集中質量的方式簡化儀表、車身覆蓋件等對手把振動影響較小的零部件；為避免發(fā)動機激勵力通過自身作用到其他結構路徑上，拆除發(fā)動機總成[7]。建立手把振動研究模型如圖1所示。約束前后輪所有自由度以模擬實際振動臺架試驗的邊界條件。

圖1 整車有限元模型Fig.1 Vehicle finite element model

2.2 模型驗證

用發(fā)動機激勵仿真得到的手把振動加速度與試驗結果進行比較分析以驗證模型準確性。首先識別試驗下的發(fā)動機激勵，考慮發(fā)動機與車架左右各3個懸置之間為通過螺栓的硬連接，故應用逆矩陣法[7]識別。其表達如式(1)所示。

(1)

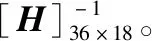
(2)

式中：ωi為第i個1/3倍頻帶的加權系數(shù)[9];ai為第i個1/3倍頻帶加速度均方根值。

(3)

式中，av為三軸向總加權加速度均方根值。

將手把WRMS仿真結果與試驗進行對比分析，限于篇幅，這里以發(fā)動機轉速6 500 r/min時的手把振動為例進行對比分析，如圖2—圖4所示。

由圖2—圖4可知，手把各軸向加速度響應的峰值頻率基本一致且其所對應幅值的最大誤差小于10%，可以接受。驗證其余發(fā)動機轉速下的手把振動加速度響應，如圖5所示。

圖2 手把x向加速度對比Fig.2 Compare the x-acceleration of the handlebar

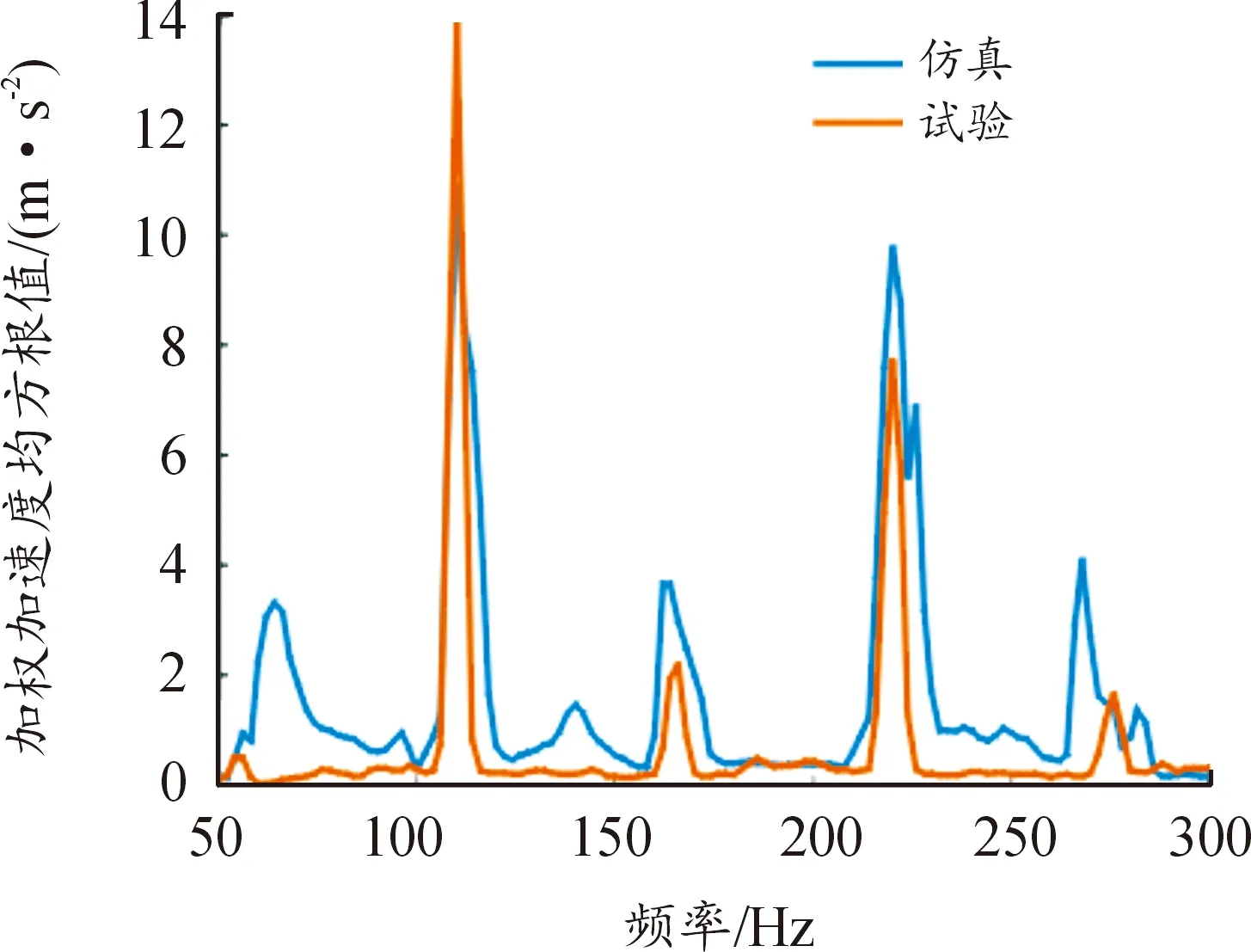
圖3 手把y向加速度對比Fig.3 Compare the y-acceleration of the handlebar

圖4 手把z向加速度對比Fig.4 Compare the z-acceleration of the handlebar

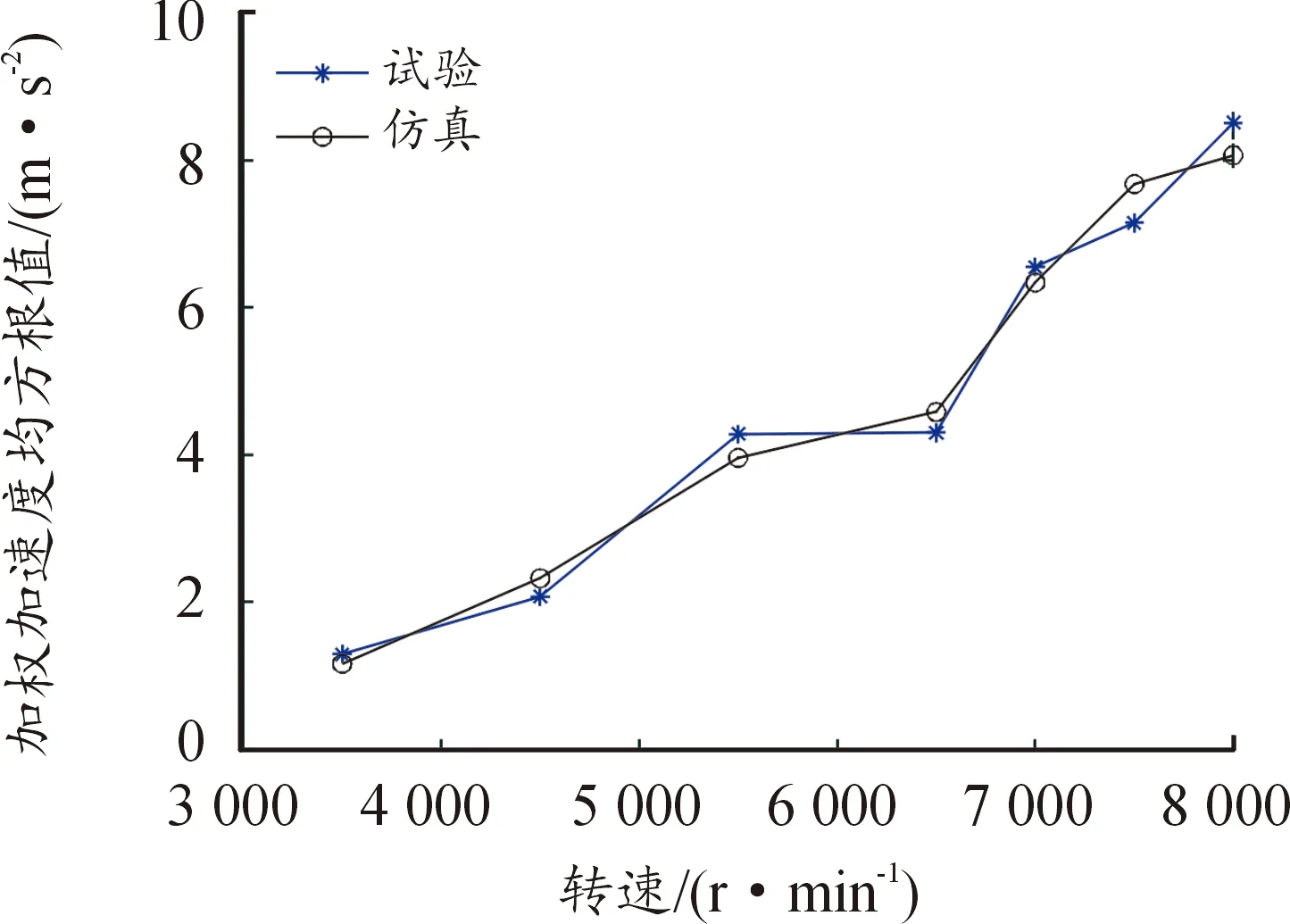
圖5 手把振動對比分析Fig.5 Comparative analysis of handle vibration

圖5可知，仿真與試驗間的均方根誤差較小，為0.33 m/s2，且WRMS變化趨勢一致，判斷模型準確可用。

3 手把TMD的參數(shù)設計

經(jīng)整車模態(tài)分析發(fā)現(xiàn)手把有頻率為122.8 Hz的手把第一階振動模態(tài)，如圖6所示。其在發(fā)動機轉速7 300 r/min基頻附近會發(fā)生共振。為抑制共振峰在手把管末端引入調諧質量阻尼器TMD(圖7所示)并以122.8 Hz作為調諧頻率。

圖6 手把第一階局部振動模態(tài)Fig.6 The first local vibration mode of the handle

圖7 TMD安裝示意圖Fig.7 TMD installation diagram

3.1 TMD振動模型的建立

考慮手把TMD實際安裝方式，以TMD在手把圓管內任一徑向振動為例，建立手把嵌入式TMD二自由度振動模型，如圖8所示。

圖8 嵌入式TMD二自由度振動模型Fig.8 Embedded TMD two-degree-of-freedom vibration model

圖8中，M、K分別為從手把管末端觀察到的手把第一階振動模態(tài)的等價質量和等價剛度；m為TMD的集中質量；k、c分別為TMD在任一徑向的剛度系數(shù)和阻尼系數(shù)；x1、x2分別為M、m的絕對位移；f為振動系統(tǒng)的簡諧激勵力。振動系統(tǒng)的動力學方程為

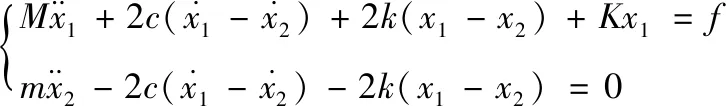
(4)

人體對手把振動的感知與加速度的大小有關，故以抑制手把振動加速度響應為目標設計TMD。應用Den Hartog定點理論[10]，由式(4)計算出最優(yōu)同調條件和最優(yōu)阻尼條件如式(5)和式(6)所示。

(5)

(6)

式中：u為質量比m/M；γ為固有頻率比fm/fM；ξ為TMD的阻尼比c/(2πmfM)。

聯(lián)合式(5)、式(6)得TMD最優(yōu)剛度和最優(yōu)阻尼：

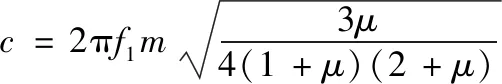
TMD振動模型針對單自由度主振系，而摩托車手把為一連續(xù)結構，故需識別出TMD安裝位置處(手把末端)具有物理含義的等價質量M和等價剛度K。

3.2 等價質量與等價剛度識別

等價質量識別法主要有固有模態(tài)法、正交多項式識別法和質量感應法[11]。考慮摩托車手把為連續(xù)體，采用質量感應法。質量感應法把對象結構作為一個單自由度系統(tǒng)，在TMD預安裝位置附加一個給定的質量，根據(jù)對象結構的固有頻率的變化來決定等價質量的大小。該方法原理示意如圖9所示。

圖9 質量感應法原理示意Fig.9 Schematic diagram of the mass induction method

從手把末端觀察到的手把第一階局部振動模態(tài)的等價質量和等價剛度可由式(9)給出。

(9)

式中：Δm為施加在手把管末端的附加質量；fM為手把第一階振動模態(tài)頻率122.8 Hz；fΔm為手把管末端附加質量后的手把第一階振動模態(tài)頻率。

附加質量的大小是影響識別精度的重要因素，若附加質量太小，則固有頻率的變化不明顯，將增加識別誤差；附加質量太大，因相鄰模態(tài)耦合也會增加識別誤差。為減小誤差，采用數(shù)個不同附加質量進行等價質量識別，以附加質量大小作為橫坐標，計算出的等價質量作為縱坐標，利用最小二乘法擬合來預測等價質量(附加質量為0時的等價質量)，如圖10所示。由圖10可知等價質量為M=394.20 g，根據(jù)式(9)計算出等價剛度為K=234.68 N/mm。

圖10 等價質量識別曲線Fig.10 Equivalent quality identification curve

3.3 TMD減振效果預測

TMD滿足最優(yōu)同調、最優(yōu)阻尼時的振動系統(tǒng)傳遞函數(shù)的最大振幅比以及減振帶寬都由質量比μ決定。質量比越高，振幅比越小，減振帶寬越寬[12]，但同時要避免增加過多質量致使手把操控困難。為符合工程實際，設定手把TMD質量為110 g，計算質量比u為0.28，按式(7)、式(8)設計TMD的剛度k和阻尼c分別為86.38 N/mm和0.28 N·s/mm。

在Hypermesh中，采用CBUSH單元模擬TMD剛度和阻尼[13]，以集中質量代替TMD質量，如圖11所示。

圖11 TMD模擬圖Fig.11 TMD simulation diagram

考慮該車發(fā)動機為單缸四沖程，常用轉速范圍為2 000～8 000 r/min。此外，發(fā)動機激勵主要表現(xiàn)為往復慣性力基頻、1.5倍頻、2倍頻，而二階以上的影響很小，故在發(fā)動機各懸置點施加300 Hz內的單位掃頻力以模擬發(fā)動機在整個頻帶內的激勵，計算手把與手掌接觸點的各軸加速度響應，如圖12—圖14所示。

由圖12—圖14可知，針對手把第一階振動模態(tài)頻率122.8 Hz設計的最優(yōu)調諧質量阻尼器TMD顯著降低了該頻率下的共振峰，同時，除部分頻率附近出現(xiàn)了可以接受的振動加速度少量增加外，其余頻率下的振動加速度均未出現(xiàn)惡化。根據(jù)ISO 5349手把振動評價標準，計算出單位掃頻激勵下手把振動總加權加速度均方根值WRMS，如表2所示。結果表明TMD抑制了37.8%手把振動加權加速度均方根值，振動抑制效果明顯。

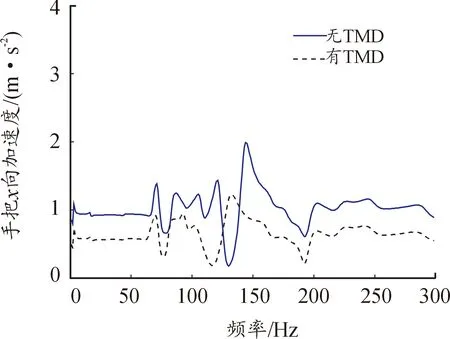
圖12 手把x向加速度響應Fig.12 The x acceleration response of the handle

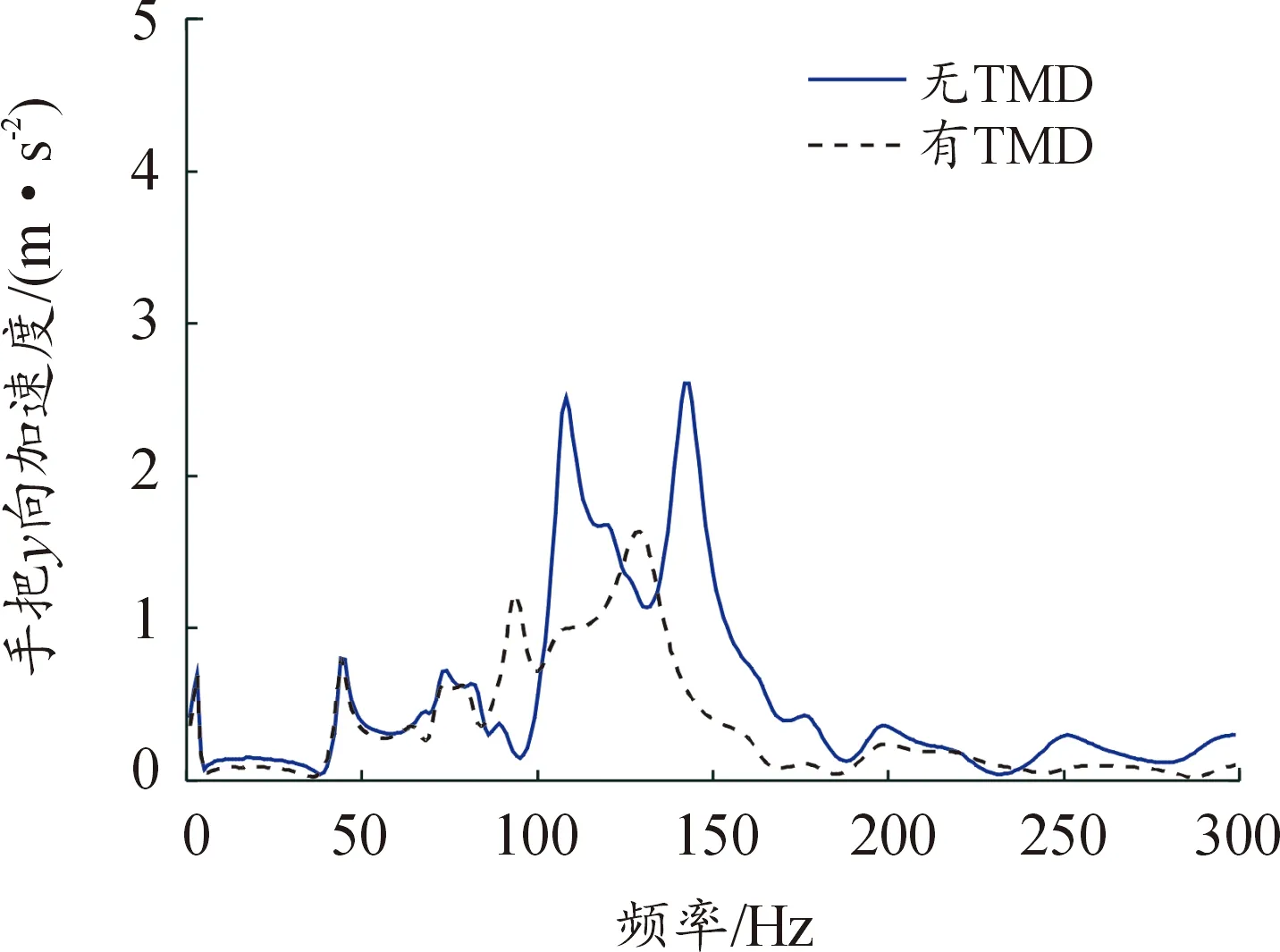
圖13 手把y向加速度響應Fig.13 The y acceleration response of the handle

圖14 手把z向加速度響應Fig.14 The z acceleration response of the handle

表1 手把振動加權加速均方根值Table 1 Weighted root mean square acceleration value of handle vibration

4 結論

1) 考慮手把調諧質量阻尼器TMD安裝方式，提出一種用于減小手把振動的嵌入式TMD模型。

2) 以人體感受更敏感的手把振動加速度為嵌入式TMD減振設計目標。結合定點理論、等價質量和等價剛度識別法確定了嵌入式TMD最優(yōu)減振設計參數(shù)，為摩托車手把TMD設計提供參考。

3) 通過發(fā)動機激勵下的手把振動響應分析驗證所設計TMD的減振效果。結果表明：所設計TMD對手把振動有顯著抑制效果，其總加權加速度均方根值減小了37.8%，表明了設計方法的有效性。