基于多目標(biāo)鯨魚優(yōu)化算法的動態(tài)武器目標(biāo)分配
邱少明,柏陳城,呂亞娜,李 傲
(大連大學(xué) 通信與網(wǎng)絡(luò)重點實驗室,遼寧 大連 116622)
1 引言
武器目標(biāo)分配(weapon target assignment,WTA)問題是戰(zhàn)場上作戰(zhàn)指揮與控制(C2)[1]自動化的關(guān)鍵問題之一,是軍事運籌學(xué)領(lǐng)域中典型的帶有約束條件的非線性組合優(yōu)化問題,并且已被證明是NP(non-deterministic polynomial)完全問題[2]。它的基本目標(biāo)是在武器資源有限的情況下,產(chǎn)生的武器打擊分配方案,使得武器對來襲目標(biāo)的毀傷程度最大化。武器目標(biāo)分配的最優(yōu)化是充分發(fā)揮武器系統(tǒng)的作戰(zhàn)效能,達(dá)到對敵最佳毀傷效果的重要因素[3]。
WTA通常被分為兩類,一類是靜態(tài)武器目標(biāo)分配(static weapon target assignment,SWTA),另一類是動態(tài)武器目標(biāo)分配(dynamic weapon target assignment,DWTA)[4]。SWTA模型中,已知該問題的所有參數(shù),在一次武器打擊過程中將所有武器分配完,而DWTA模型,是武器平臺的武器分成幾個階段打擊目標(biāo),并且一個階段產(chǎn)生的武器分配方案對目標(biāo)的毀傷效果,影響下一個階段的交戰(zhàn)分配策略,是一個動態(tài)決策的過程[5]。
使用武器打擊來襲目標(biāo),并獲取最佳的打擊收益,受武器資源、目標(biāo)威脅和武器成本等多方面的戰(zhàn)場環(huán)境約束。DWTA是一個多階段的分配過程,在整個決策過程中需考慮其不斷變化的戰(zhàn)場信息,打擊目標(biāo)過程通常采用“觀察-射擊-觀察”的策略[6],因此DWTA要比SWTA要復(fù)雜很多。現(xiàn)有的WTA研究,主要集中在SWTA的研究,在早期,SWTA問題主要使用枚舉法,分支定界算法,動態(tài)規(guī)劃等傳統(tǒng)算法進(jìn)行求解[7-8],伴隨著智能算法的興起和計算機技術(shù)的快速發(fā)展,出現(xiàn)了進(jìn)化算法[9]、粒子群算法[10]、模擬退火[11]等優(yōu)化算法。例如,Jun Wang等[12]將灰狼優(yōu)化算法與本地搜索算法結(jié)合提出HDGWOA算法,驗證了所提算法的可行性和大規(guī)模WTA問題可擴展性。王力超等[13]提出改進(jìn)粒子群優(yōu)化算法,提高求解武器目標(biāo)分配問題算法的效率和準(zhǔn)確性。王平等提出用模擬退火算法對WTA問題進(jìn)行求解,但在具體的實驗中,參數(shù)的選擇有局限性。相對來說只有較少的關(guān)于DWTA問題的研究,Bin Xin等[14]通過設(shè)計本地搜索運算符,避免重復(fù)產(chǎn)生相同的決策,但其求解質(zhì)量不高,計算過程過于復(fù)雜,Chyh-Ming Lai等[15]為減小算法的復(fù)雜性,提出一種簡化粒子群優(yōu)化算法,通過生成初始化方案和交換分配方案簡化計算過程,提高了目標(biāo)分配效率。Tianqing Chang等[16]針對ABC算法在求解DWTA問題中存在收斂速度慢和搜索效率低的問題,提出一種改進(jìn)ABC算法,改進(jìn)ABC結(jié)合多種啟發(fā)式因子初始化武器分配方案,提高DWTA收斂速度。但這都僅僅以目標(biāo)的毀傷程度為目標(biāo)。
為滿足現(xiàn)代化戰(zhàn)爭需求,本文建立一種以目標(biāo)生存值最小和武器消耗最小為目標(biāo),設(shè)計一種多目標(biāo)的DWTA數(shù)學(xué)模型,提出一種非支配排序的多目標(biāo)鯨魚優(yōu)化算法(Non-dominated sorting Multi-objective whale optimization algorithm,NSMWOA)用于提高尋優(yōu)精度。通過3個多目標(biāo)測試函數(shù)驗證本文算法的性能,并與NSGA-Ⅱ和MOPSO進(jìn)行比較,實驗結(jié)果表明本文所提算法尋優(yōu)能力明顯優(yōu)于其他算法,在DWTA的數(shù)學(xué)模型中進(jìn)行仿真測試,實驗結(jié)果表明本文所提算法得出PF優(yōu)于其他算法,所得出的武器分配方案更合理。
2 基本概念
2.1 多目標(biāo)優(yōu)化
多目標(biāo)優(yōu)化問題指將多個子目標(biāo)同時尋優(yōu),但是這些子目標(biāo)之間的利益存在相互沖突的問題,很難客觀地使各個子目標(biāo)都達(dá)到最優(yōu)解,所以對于一個多目標(biāo)優(yōu)化問題,沒有絕對的或者說是唯一的最好解[17]。一個多目標(biāo)優(yōu)化問題可以被描述如下所示:
minf(x)=[f1(x),f2(x),…,fn(x)]T
(1)
約束條件:
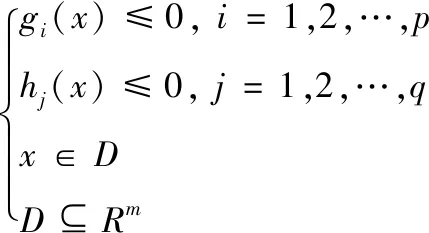
其中:x=(x1,x2,…,xi,…,xn),xi表示第i個決策變量,gi(x)≤0表示不等式約束條件,hi(x)≤0表示等式約束條件,D表示n維決策空間,Rm表示基本空間。
任意的2個決策變量xa,xb,如果滿足下面2個條件,則稱xa支配xa。
1)?i∈{1,…,n},都有fi(xa)≤fi(xb)成立。
2)?i∈{1,…,n},都有fi(xa) 所有非支配解的集合稱為非支配集或非劣解集,對于不存在其他決策變量能支配該變量,則稱該決策變量為非支配解。在n維決策空間中,多個目標(biāo)函數(shù)都找不到其他的解能夠優(yōu)于當(dāng)前解,則稱該解為Pareto最優(yōu)解。所有的Pareto最優(yōu)解構(gòu)成Pareto最優(yōu)解集,所有Pareto最優(yōu)解組成的曲面為Pareto前沿。對于單目標(biāo)優(yōu)化問題與多目標(biāo)優(yōu)化問題相比較,一個很大的區(qū)別就是多目標(biāo)的解并不是唯一的,而是存在一個最優(yōu)解的集合。 鯨魚優(yōu)化算法(whale optimization algorithm,WOA)是2016年由Seyedali Mirjalili教授提出的一種群智能優(yōu)化算法,通過模仿鯨魚在海洋中捕捉食物的搜尋過程,來尋找最優(yōu)解。該算法具有結(jié)構(gòu)簡單、自身參數(shù)少的特點,在多元函數(shù)求解方面比傳統(tǒng)粒子群優(yōu)化算法和遺傳算法的速度更快、精度更高[18]。 座頭鯨能夠識別獵物的位置并將其包圍,鯨魚優(yōu)化算法的數(shù)學(xué)模型包括以下3個方面:搜索獵物、包圍獵物和泡泡網(wǎng)攻擊[19]。 1) 搜索獵物。座頭鯨根據(jù)彼此間的位置信息隨機搜索獵物,數(shù)學(xué)模型如下: D1=|C·Xrand(t)-X(t)| (2) X(t+1)=Xrand(t)-A·D1 (3) 其中:Xrand(t)表示隨機選擇的鯨魚位置,X(t)表示當(dāng)前鯨魚的位置信息,D1表示隨機選擇的鯨魚與當(dāng)前鯨魚之間的距離,t表示當(dāng)前的迭代次數(shù),A,C表示向量系數(shù),定義如下: 其中:a是從2線性減小到0的收斂因子,r表示0~1之間的隨機數(shù)。 2) 包圍獵物。座頭鯨在找到獵物后將其包圍,數(shù)學(xué)模型如下所示: D2=|C·X*(t)-X(t)| (4) X(t+1)=X*(t)-A·D2 (5) 其中:X*(t)表示獵物的位置,D2表示當(dāng)前鯨魚距離獵物個體之間的位置距離。 3) 泡泡網(wǎng)攻擊。座頭鯨在找到獵物后以螺旋方式不斷減小包圍范圍,數(shù)學(xué)模型如下: D3=|X*(t)-X(t)| (6) X(t+1)=D3·ebl·cos(2πl(wèi))+X*(t) (7) 其中:D3表示當(dāng)前鯨魚距離獵物之間的位置距離,b表示螺旋方式的常數(shù),l表示[-1,1]之間的隨機數(shù)。 DWTA模型與SWTA有很多類似的地方,但DWTA是一個多階段的武器目標(biāo)分配問題,前一個階段的分配結(jié)果產(chǎn)生的打擊收益會對下一個階段的分配方案產(chǎn)生影響。簡單的說,SWTA在整個防御階段由武器和目標(biāo)配對構(gòu)成,DWTA是由武器、目標(biāo)和階段3個進(jìn)行配對組成,DWTA可以簡單看出是多個階段的SWTA[20]。 (8) (9) 約束條件: 其中,式(8)、式(9)是建立DWTA的2個目標(biāo)函數(shù),F(xiàn)1和F2分別表示目標(biāo)生存期望值和武器打擊成本,約束1表示在每個階段中,武器打擊目標(biāo)的能力,通常ni設(shè)置為1,表示一個武器在同一階段對一個目標(biāo)打擊一次,約束2表示武器的彈藥量,使用的武器數(shù)量不能超出武器所擁有的數(shù)量,約束3中xij取值范圍1或者0,表示打擊或者不打擊。 Mirjalili等在2016年提出的WOA算法是一種模擬座頭鯨的覓食行為的群體智能優(yōu)化算法,其中通過最佳搜索代理來模擬捕獵行為,使得WOA本身具有精英指導(dǎo)能力,但WOA算法本身鯨魚位置是隨機初始化,可能出現(xiàn)種群聚集的情況,并且該算法只能求解單個目標(biāo)函數(shù)問題,對于多目標(biāo)優(yōu)化問題無法處理。Logistic映射是一種非常簡單卻被廣泛應(yīng)用的經(jīng)典混沌映射,該模型看來似乎很簡單,并且是確定性的,但具有極為復(fù)雜的動力學(xué)行為,Logistic映射序列還具有較好的自相關(guān)性和互相關(guān)性[21]。因此,本文通過兩次logistic映射初始化種群,使得種群分布均勻,對鯨魚種群間個體進(jìn)行支配關(guān)系和擁擠度進(jìn)行排序,對傳統(tǒng)WOA進(jìn)行改進(jìn),使得改進(jìn)WOA算法可以解決多目標(biāo)優(yōu)化問題的能力。 圖1 DWTA分配編碼Fig.1 DWTA assignment code h1表示第一個打擊階段,h2表示第二個打擊階段,Wi表示第i個武器單元,Ti表示打擊的目標(biāo)單位,取值范圍為 [1,n]之間的整數(shù)。 群智能優(yōu)化算法中初始種群位置的選取對算法的收斂速度和尋優(yōu)精度的影響是至關(guān)重要的,一個分布均勻的種群,有利于算法搜索范圍更廣,提高收斂精度,相反一個隨機產(chǎn)生的種群,造成的種群個體將分布不均衡,導(dǎo)致算法搜索速度慢,增加算法陷入局部最優(yōu)的概率。Logistic映射是經(jīng)典的混沌映射之一,具有計算量小,易實現(xiàn)的特點,而在WOA算法中,鯨魚種群間個體都是采用隨機初始化的,為增加這種隨機性,采用Logistic映射初始化種群,表達(dá)式如下所示: zk+1=uzk(1-zk)zk∈(0,1) (10) 其中,μ∈[0,4],當(dāng)3.569 945≤μ≤4時,Logistic映射才具有混沌性質(zhì),但Logistic本身產(chǎn)生的偽隨機序列,兩端部分的分布情況相比其他部分過于密集,為增加混沌效果,本文采用兩次Logistic映射初始化,在第一次Logistic映射產(chǎn)生的鯨魚位置信息的基礎(chǔ)上,在增加一次Logistic映射,使得種群間分布均勻。 由于智能優(yōu)化算法在迭代過程中存在部分的隨機性,有時產(chǎn)生的子代個體并沒有父代個體優(yōu)秀,另一方面,有些父代個體雖沒有其子代個體優(yōu)秀,但優(yōu)于其他子代個體,如果只是簡單的將子代個體替換父代個體,降低了算法的收斂精度。因此,本文中先將父代與子代個體合并,對合并后的種群根據(jù)非支配等級和擁擠度大小進(jìn)行排序,保留優(yōu)秀個體。 4.3.1非支配等級 WOA算法只適合處理目標(biāo)函數(shù)只有一個的問題,而對于擁有多個優(yōu)化目標(biāo)的函數(shù)問題來說,鯨魚個體對應(yīng)的多個目標(biāo)函數(shù)值之間存在相互沖突的問題,由于無法處理各個目標(biāo)函數(shù)值之間的關(guān)系,導(dǎo)致WOA無法處理這類問題。為此,將鯨魚個體間引入一種非支配關(guān)系,計算出每個個體的非支配等級,進(jìn)而比較種群間個體的優(yōu)劣,非支配等級計算具體流程如下所示: Step1 遍歷鯨魚種群個體,計算每個個體的被支配個數(shù)和支配解的集合; Step2 找出被支配個數(shù)為0的個體,記為第一支配層; Step3 將第一支配層的個體,從剩余個體中刪除,剩余個體的支配個數(shù)減一; Step4 重復(fù)Step2-Step3步驟,算出其他層的支配個體,直到鯨魚種群分層完為止。 4.3.2擁擠度大小 對于合并后的種群,如果只是篩選非支配等級高的個體,導(dǎo)致種群個體出現(xiàn)聚集的情況,不利于算法的全局尋優(yōu),為增加種群的多樣性,通過計算種群中距離最近的兩個個體之間形成的面積,稱為擁擠度。擁擠度越小,表明當(dāng)前種群間的分布越密集,反之,表明種群之間的多樣性越大。在相同的非支配等級下根據(jù)每一目標(biāo)函數(shù)值的大小的升序順序?qū)ΨN群進(jìn)行排序,其中邊界解指定為無窮大的解,鯨魚個體i的擁擠度等于與i相鄰的2個個體i+1和i+1之間形成的矩形邊長和,擁擠度具體計算過程如下: Step1 初始化種群個體擁擠度di=0; Step2 根據(jù)目標(biāo)函數(shù)值,對非支配等價相同的個體進(jìn)行排序,并記錄最大的目標(biāo)函數(shù)值fmax,fmin。 Step3 將非支配等價相同的個體的邊界指定為無窮大,其他鯨魚個體根據(jù)di=di+(fk(i+1)-fk(i-1))/(fmax-fmin)計算擁擠度計算; 基于多目標(biāo)鯨魚優(yōu)化算法的DWTA問題的步驟描述如下: Step1 初始化鯨魚種群大小NP,最大迭代次數(shù)tmax,通過2次Logistic映射生成分布均勻的鯨魚種群; Step2 根據(jù)式(2)—式(7)產(chǎn)生第一代鯨魚種群,當(dāng)前代與新產(chǎn)生的一代進(jìn)行合并; Step3 計算合并后所有鯨魚個體的非支配等級并依據(jù)該等級從小到大排序; Step4 在Step3的順序上,計算非支配等級相同的個體的擁擠度大小,并對等級相同的個體進(jìn)行擁擠度從大到小排序; Step5 根據(jù)Step3、Step4的排序結(jié)果,篩選最大值作為優(yōu)秀個體,并記錄最優(yōu)鯨魚個體位置信息x(t); Step6t=t+1,判斷是否達(dá)到最大迭代次數(shù),若是,輸出武器目標(biāo)分配方案,否則跳轉(zhuǎn)到Step2。 為了驗證本文中所提NSMWOA算法的優(yōu)勢,測試3個多目標(biāo)函數(shù)ZDT1,ZTD2,ZTD3,與NSGA-Ⅱ[22],MOPSO[23]作對比實驗。另外,因為原始WOA算法存在一定的缺陷,無法解決多目標(biāo)問題,所以本文中未加入消融實驗。為保證實驗的公平性,所有測試都在Windows 10(64位)操作系統(tǒng),編程軟件使用MATLAB R2016a的計算機上設(shè)計實現(xiàn)。3種算法的種群大小均為50,迭代次數(shù)均為100。為減小算法在測試函數(shù)中帶來的隨機性,獨立重復(fù)20次實驗并記錄各個評價指標(biāo)的平均值,如表2所示。仿真結(jié)果如圖2—圖4所示。 表1 3個多目標(biāo)測試函數(shù)Table 1 3 multi-objective test functions 表2 3個函數(shù)評價指標(biāo)平均值Table 2 Average value of evaluation indexes of the three functions 從圖2—圖4中可以看出,本文中所提算法相比文獻(xiàn)[19]NSGA-Ⅱ和文獻(xiàn)[21]MOPSO算法更加貼近真實的Pareto前沿,表明本文算法尋優(yōu)精度明顯優(yōu)于其他算法,為減小文章篇幅,只列出3個算法在ZTD1函數(shù)上的世代距離(GD)、反世代距離(IGD)、超體積指標(biāo)(HV)、空間度量指標(biāo)(Spacing)指標(biāo)來說明算法的性能,如圖5—圖8所示。 圖2 ZDT1測試曲線Fig.2 ZDT1 test curve 圖3 ZDT2測試曲線Fig.3 ZDT2 test curve 圖4 ZDT3測試曲線Fig.4 ZDT3 test curve 圖5 GD曲線Fig.5 GD curve 圖6 HV曲線Fig.6 HV curve 圖7 IGD曲線Fig.7 IGD curve 圖8 Spacing曲線Fig.8 Spacing curve 如表2所示,GD值越小,說明算法的收斂性越好,HV值越大,說明算法的綜合性越好,IGD值越小,說明算法的綜合性越好,Spacing值越小,說明該解集越均勻。從圖可以看出NSMWOA算法在收斂性、綜合性能明顯優(yōu)于其他算法。平均提升效果均在34%以上,其中,在目標(biāo)函數(shù)ZDT2中的HV指標(biāo)上更是有223.837%的提升效果。 假設(shè)某次軍事行動中,有10種類型的武器平臺打擊8個來襲目標(biāo),每個武器平臺所用的武器數(shù)量均為2,每個武器在每個階段只能使用一次,并且武器只能打擊一個目標(biāo),武器對目標(biāo)的毀傷概率、目標(biāo)的價值以及武器每個階段的使用成本值采用文獻(xiàn)[24]方法生成。以目標(biāo)函數(shù)式(8)、式(9)為DWTA模型,種群大小和迭代次數(shù)均設(shè)置為100,對比算法求解DWTA問題得出的Pareto前沿,如圖9所示。 圖9 3種算法得出DWTA的Pareto前沿對比Fig.9 Pareto frontier comparison of DWTA obtained by the three algorithms 為了增加實驗的公平性,將獨立重復(fù)運行20次,取函數(shù)F1、函數(shù)F2的平均值。為了便于分析,表3展示了3種算法的武器成本F2為13.21時,對應(yīng)的目標(biāo)函數(shù)F1的值,由于函數(shù)F1是毀傷概率的倒數(shù),F(xiàn)1值越小,表明毀傷效果值就越大,由表3中數(shù)據(jù)可知本文所提算法的在武器成本一樣的情況下,得出的武器分配方案使得目標(biāo)的毀傷效果最大。 表3 3種算法性能對比Table 3 Performance comparison of the three algorithms 本文中建立一種多目標(biāo)優(yōu)化的動態(tài)武器目標(biāo)分配模型,并提出一種多目標(biāo)鯨魚優(yōu)化算法用于求解,首先通過兩次logistic映射對鯨魚種群進(jìn)行初始化,使得種群分配均勻,其次合并父代與子代種群,并引入非支配等級和擁擠度大小對種群間個體進(jìn)行排序,篩選優(yōu)秀個體。通過與其他算法在3個多目標(biāo)函數(shù)中,獨立重復(fù)20次實驗記錄的各個評價指標(biāo)的平均值表明,本算法的在Spacing、IGD、HV、GD上均有不小于34%的效果提升,收斂較好;在動態(tài)武器目標(biāo)分配模型測試中,在打擊成本相同的前提下,所得出的分配方案使得目標(biāo)的毀傷效果最好,尋優(yōu)精度更高。2.2 鯨魚優(yōu)化算法

3 動態(tài)武器目標(biāo)分配數(shù)學(xué)模型
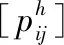

4 多目標(biāo)鯨魚優(yōu)化算法求解DWTA
4.1 編碼

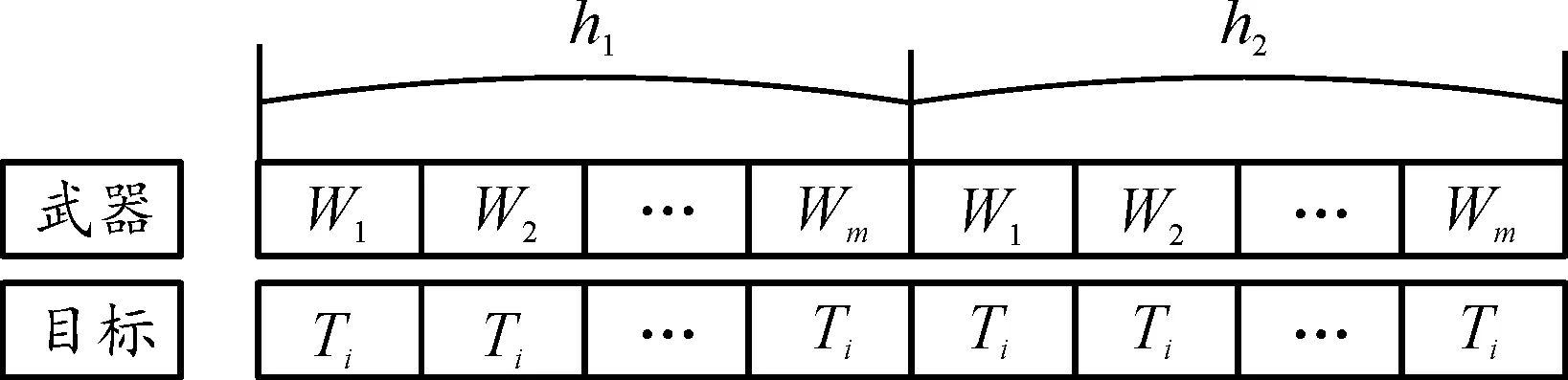
4.2 種群初始化
4.3 排序
4.4 算法流程
5 仿真與分析
5.1 多目標(biāo)函數(shù)測試函數(shù)



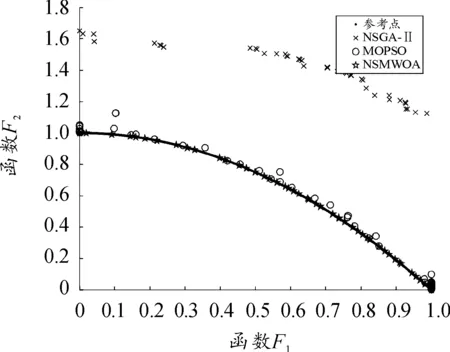
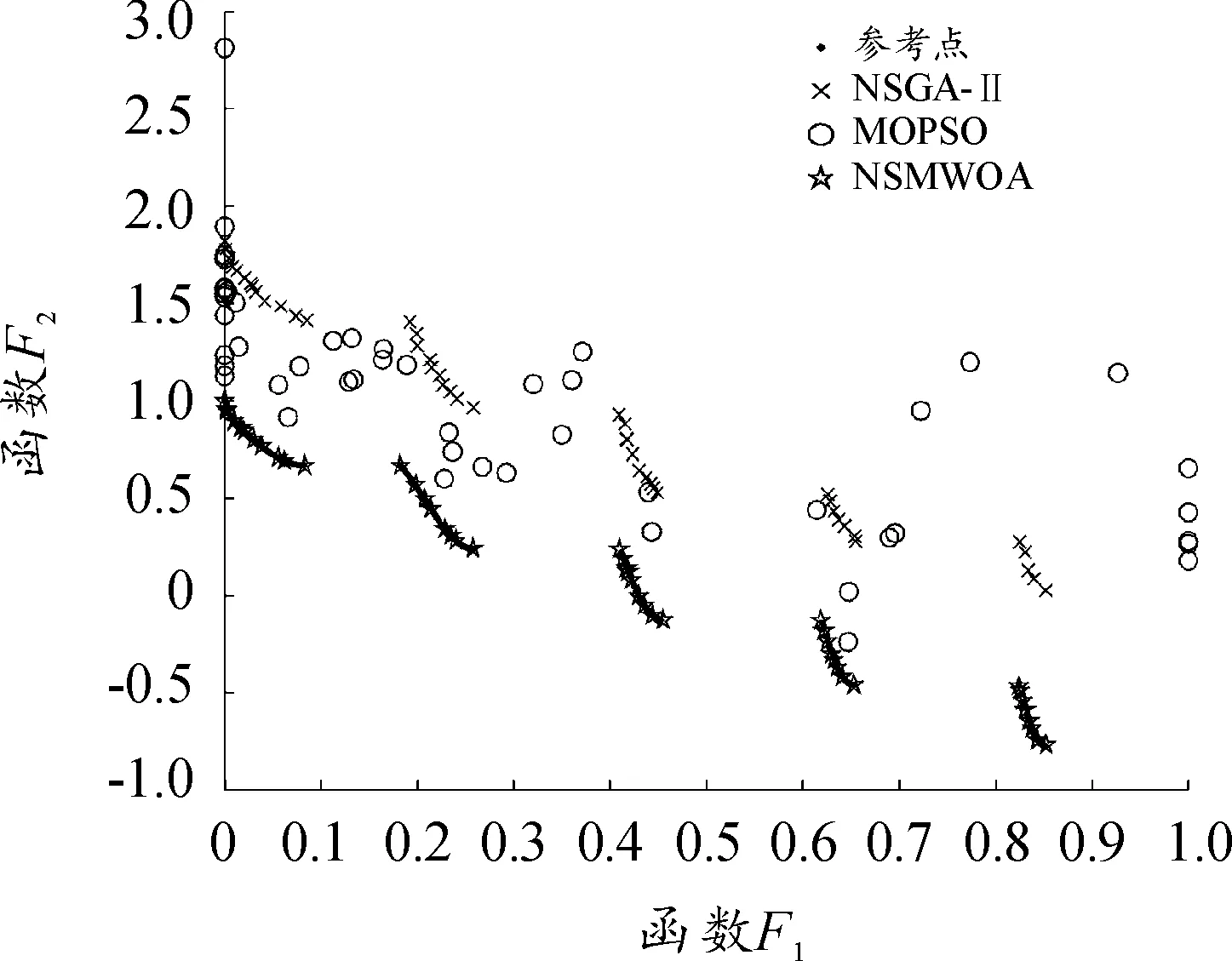

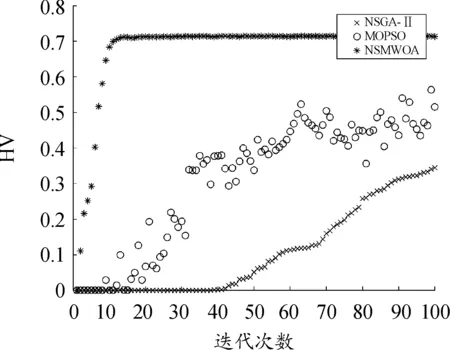
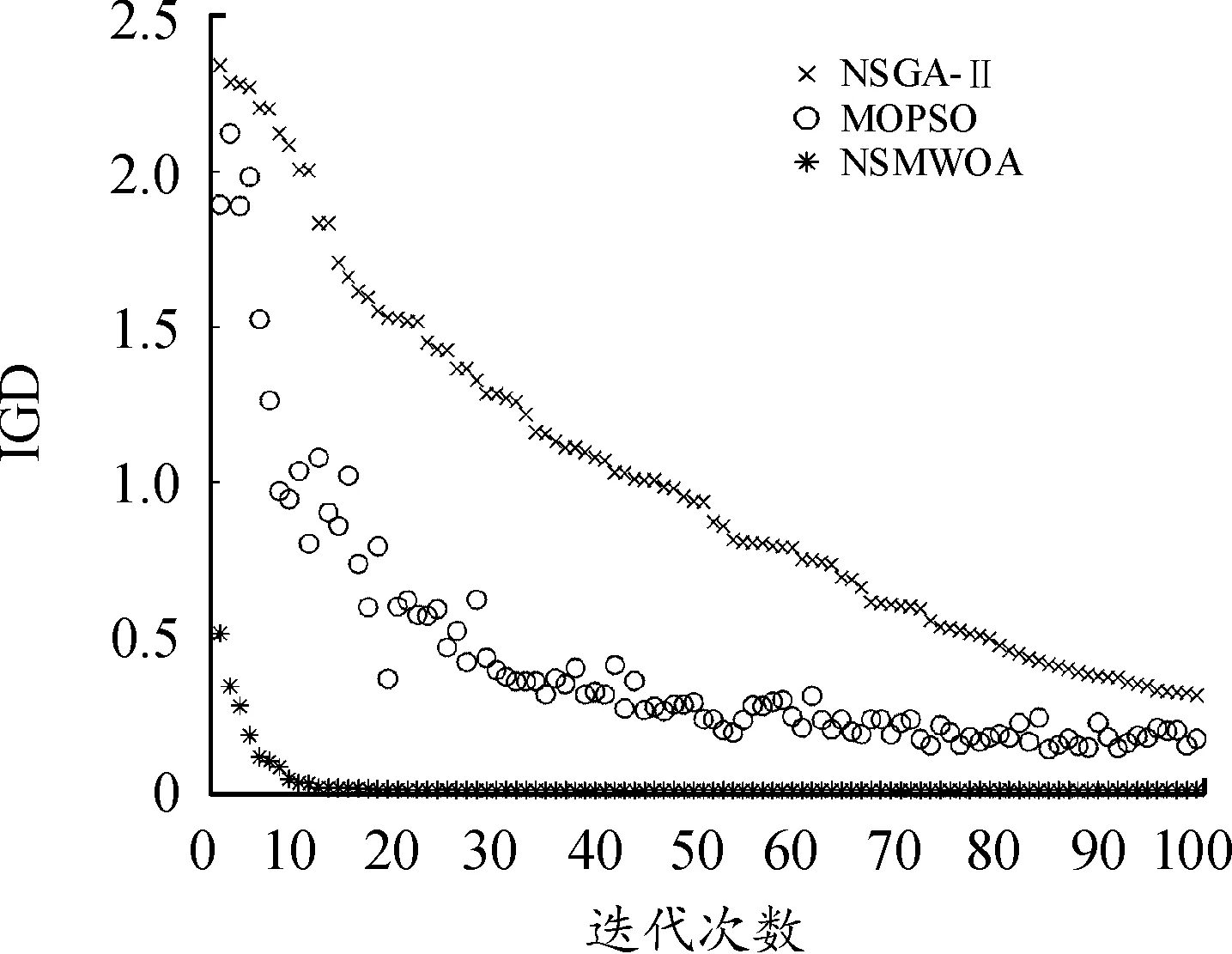
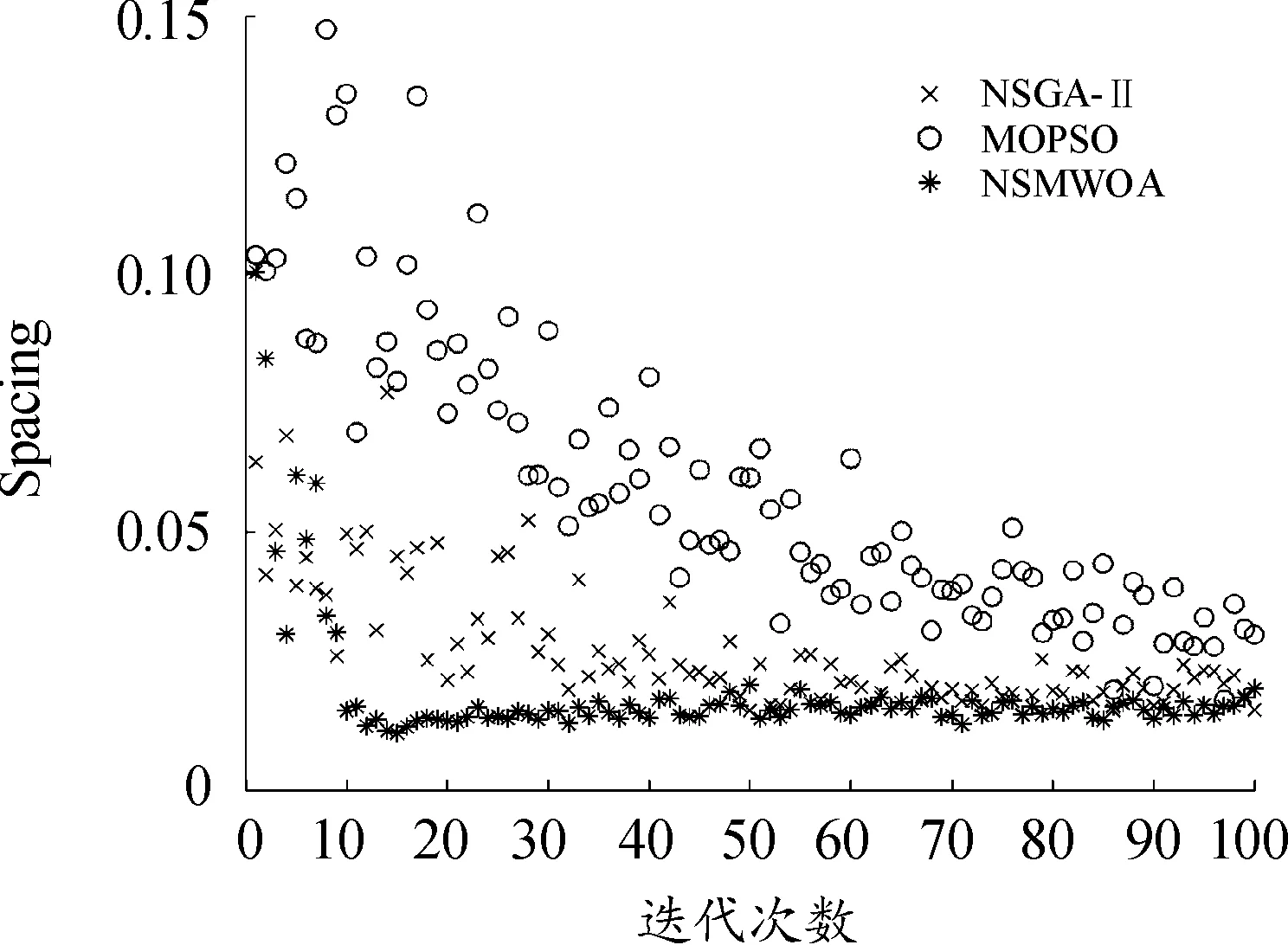
5.2 NSMWOA在DWTA分配中的應(yīng)用


6 結(jié)論

