基于增量預(yù)測(cè)控制的高速多體船垂向運(yùn)動(dòng)穩(wěn)定研究

許煒東,張 軍,仲銘杰,楊一帆

(1.江蘇大學(xué) 電氣信息工程學(xué)院,江蘇 鎮(zhèn)江 212013; 2.江蘇航空職業(yè)技術(shù)學(xué)院,江蘇 鎮(zhèn)江 212013)

1 引言

高速多體船(包括兩體船和三體船)是當(dāng)前新型船舶的重要發(fā)展趨勢(shì)之一，與單體船相比具有更小的興波阻力、橫向穩(wěn)定性好、裝載量大、抗打擊能力強(qiáng)，在軍事、航運(yùn)領(lǐng)域有著廣泛的應(yīng)用前景[1]。然而，高速多體船細(xì)長(zhǎng)的側(cè)體結(jié)構(gòu)使得縱向恢復(fù)力矩變小，造成船舶在高速航行時(shí)會(huì)產(chǎn)生較大的升沉和縱搖幅度，出現(xiàn)“埋首”運(yùn)動(dòng)[2]，嚴(yán)重破壞船體結(jié)構(gòu)。劇烈的升沉和縱搖運(yùn)動(dòng)產(chǎn)生較大的垂向加速度，造成乘客暈船、儀器失靈。因此，如何保證高速多體船的垂向運(yùn)動(dòng)穩(wěn)定，減少升沉和縱搖運(yùn)動(dòng)幅度，成為該領(lǐng)域研究的重點(diǎn)。目前，在多體船船體上安裝主動(dòng)式T型翼和壓浪板兩類附體可實(shí)現(xiàn)閉環(huán)減搖控制，T型翼可以提高船體的附加質(zhì)量和阻尼，壓浪板用于改變船體縱傾[3]。

安裝T型翼和壓浪板的高速多體船是多輸入輸出系統(tǒng)，升沉和縱搖運(yùn)動(dòng)存在強(qiáng)耦合，并且航速較高導(dǎo)致水動(dòng)力參數(shù)變化劇烈，模型具有快時(shí)變性、強(qiáng)不確定性等特點(diǎn)[4-5]。文獻(xiàn)[4]中設(shè)計(jì)解耦的比例微分(PD)控制律實(shí)現(xiàn)雙體船的垂向穩(wěn)定控制，但是需要精確辨識(shí)水動(dòng)力學(xué)參數(shù)。文獻(xiàn)[5]中提出擴(kuò)張觀測(cè)器和PD結(jié)合的解耦控制策略，提高了魯棒性。文獻(xiàn)[6]中設(shè)計(jì)定量反饋控制律，但是控制性能比較保守。文獻(xiàn)[7]中提出有限時(shí)間控制器和有限時(shí)間觀測(cè)器復(fù)合的控制策略，增強(qiáng)了多體船抑制海浪擾動(dòng)的能力。上述研究主要從鎮(zhèn)定角度來設(shè)計(jì)解耦或者魯棒控制器，沒有考慮垂向控制性能的優(yōu)化，而垂向控制目的是實(shí)現(xiàn)升沉和縱搖變化幅度和加速度越小越好。

針對(duì)升沉和縱搖耦合的多體船垂向運(yùn)動(dòng)模型，預(yù)測(cè)控制不僅能有效處理多變量耦合，并且實(shí)現(xiàn)控制性能優(yōu)化。文獻(xiàn)[8]中提出多體船的解析預(yù)測(cè)控制，避免在線復(fù)雜的數(shù)值優(yōu)化。文獻(xiàn)[9]中對(duì)隨機(jī)海浪擾動(dòng)力和力矩進(jìn)行建模，采用卡爾曼濾波器估計(jì)狀態(tài)，提出顯式預(yù)測(cè)控制。然而，上述預(yù)測(cè)控制只考慮升沉和縱搖運(yùn)動(dòng)幅度的均方差最小，沒有考慮兩者的暫態(tài)響應(yīng)過程。實(shí)際上在海浪擾動(dòng)激勵(lì)下升沉和縱搖的輸出不僅幅度大，波動(dòng)變化率也大，造成垂向加速度很大，嚴(yán)重影響高速多體船的耐波性。針對(duì)上述問題，提出基于增量預(yù)測(cè)控制的垂向運(yùn)動(dòng)穩(wěn)定方法，其創(chuàng)新點(diǎn)為：

1) 分析隨機(jī)海浪擾動(dòng)的頻域和時(shí)域特性，基于積分?jǐn)_動(dòng)模型在線估計(jì)海浪擾動(dòng)力和力矩；為減少海浪平均擾動(dòng)力和擾動(dòng)力矩的影響，將高速多體船舶的垂向運(yùn)動(dòng)模型轉(zhuǎn)化為增量模型；

2) 為減少隨機(jī)海浪擾動(dòng)下的升沉和縱搖幅度和波動(dòng)變化率，將升沉和縱搖變化率和幅

度同時(shí)引入到優(yōu)化目標(biāo)函數(shù)中，推導(dǎo)出解析的預(yù)測(cè)控制律。

具體章節(jié)安排如下：首先，建立升沉和縱搖描述的高速多體船垂向運(yùn)動(dòng)模型，分析隨機(jī)海浪的時(shí)域特性。其次，將高速多體船的垂向運(yùn)動(dòng)模型轉(zhuǎn)化為增量模型，基于滾動(dòng)優(yōu)化策略推導(dǎo)預(yù)測(cè)控制律。最后，通過仿真驗(yàn)證所提算法的有效性。

2 高速多體船的垂向運(yùn)動(dòng)模型

高速多體船的船體是相對(duì)于中間截面對(duì)稱的，T型翼和壓浪板分別在船艏底部和船艉。在航行中通過調(diào)節(jié)T型翼和壓浪板攻角，產(chǎn)生恢復(fù)力和力矩，抵消海浪引起的擾動(dòng)力和力矩，抑制升沉和縱搖劇烈運(yùn)動(dòng)。當(dāng)在康明斯方程中考慮流體記憶效應(yīng)時(shí)[10]，基于升沉和縱搖兩自由度描述的高速多體船垂向運(yùn)動(dòng)模型為

(1)

(2)

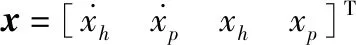
式中：ρ為海水密度；S1、S2分別為T型翼和壓浪板的有效面積；CL1和CL2分別為T型翼和壓浪板的升力系數(shù)；V表示流體相對(duì)于水翼的速度；α1、α2和lT-foil、lflap分別表示T型翼和壓浪板的攻角和力臂。

為后續(xù)設(shè)計(jì)方便，將式(1)與式(2)寫成下面的狀態(tài)空間形式

(3)

從式 (3) 可以看出，高速多體船模型存在升沉和縱搖運(yùn)動(dòng)的強(qiáng)耦合，以及存在強(qiáng)的海浪擾動(dòng)。高速多體船垂向運(yùn)動(dòng)控制目的是在海浪擾動(dòng)下，自動(dòng)調(diào)節(jié)減搖附體的攻角使得升沉和縱搖運(yùn)動(dòng)的幅度和加速度越小越好。

3 海浪擾動(dòng)力和力矩估計(jì)

高速多體船的升沉和縱搖幅度變化劇烈，主要原因是受到海浪擾動(dòng)力和力矩作用，本節(jié)研究四級(jí)海浪產(chǎn)生擾動(dòng)的時(shí)域和頻域特性，為后續(xù)的減搖控制設(shè)計(jì)提供基礎(chǔ)。本研究中采用ITTC單參數(shù)譜作為海浪仿真功率譜函數(shù)[1,11]，即

(4)

式中:h1/3為海浪有義波高；ω為海浪主導(dǎo)頻率。根據(jù)功率譜反演和隨機(jī)信號(hào)合成理論，得到作用于兩體船的擾動(dòng)力和擾動(dòng)力矩，如圖1、圖2所示。

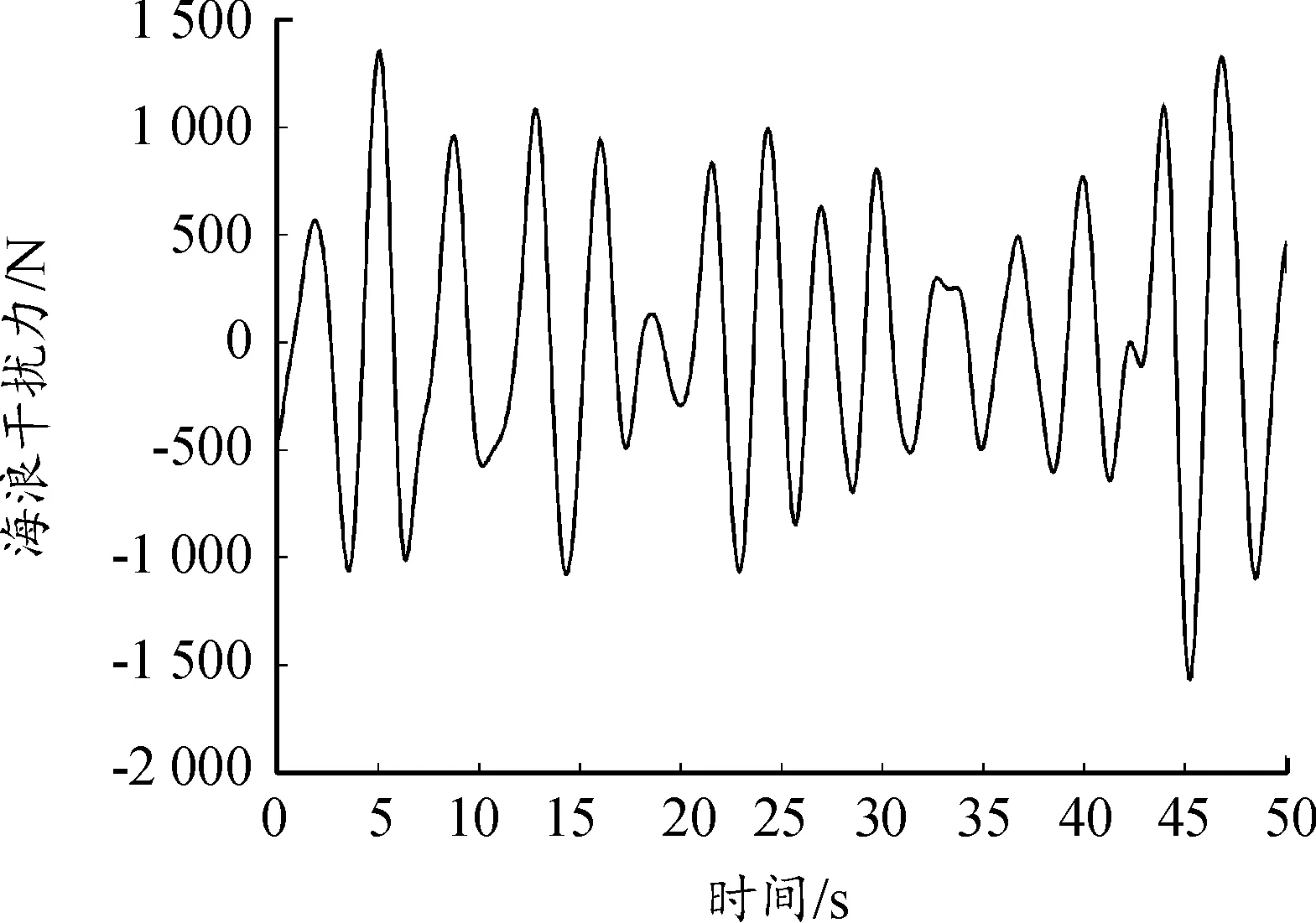
圖1 多體船的海浪擾動(dòng)力Fig.1 Disturbance wave force of the multihull

圖2 多提船的海浪擾動(dòng)力矩Fig.2 Disturbance wave moment of the multihull

可以看出多體船的擾動(dòng)力和力矩是一種平穩(wěn)隨機(jī)過程。通過統(tǒng)計(jì)數(shù)據(jù)知道海浪擾動(dòng)力和擾動(dòng)力矩均值分別為0.429 7×103N，2.028 2×103N·m，均不為零，并且海浪變化率Δd(k)≠0，這會(huì)影響下一節(jié)的預(yù)測(cè)控制模型準(zhǔn)確性，需要在線實(shí)時(shí)估計(jì)d(k)，在文獻(xiàn)[10]中假設(shè)Δd(k)=0是有局限性的。

海浪擾動(dòng)力和力矩的估計(jì)常采用白噪化方法，將白噪聲作為系統(tǒng)新的輸入，對(duì)系統(tǒng)狀態(tài)進(jìn)行擴(kuò)張，采用卡爾曼濾波器估計(jì)狀態(tài)[12]。但是，該方法需要辨識(shí)成型濾波器的參數(shù)，并且卡爾曼濾波維數(shù)較大，計(jì)算復(fù)雜。這里將海浪擾動(dòng)力和力矩作為擴(kuò)張狀態(tài)，基于積分?jǐn)_動(dòng)模型理論近似估計(jì)海浪擾動(dòng)力和力矩[13]。將高速多體船模型方程式(3) 進(jìn)行離散化可得

(5)

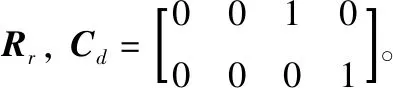
d(k+1)=d(k)+ζk(k)

(6)

其中：ζk(k)為零均值白噪聲；噪聲方差為Qr。將海浪擾動(dòng)作為狀態(tài)的一部分，擴(kuò)張后的狀態(tài)為

擴(kuò)展的隨機(jī)線性模型如下

xe(k+1)=Aexe(k)+Beu(k)+Bewζ(k)

(7)

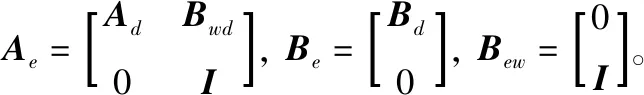
圖3 估計(jì)的海浪擾動(dòng)力Fig.3 Estimated disturbance wave force

圖4 估計(jì)的海浪擾動(dòng)力矩Fig.4 Estimated disturbance wave moment

4 減少變化率的增量預(yù)測(cè)控制

高速多體船的垂向運(yùn)動(dòng)模型方程式 (3) 是多變量，并且垂向運(yùn)動(dòng)控制目的是實(shí)現(xiàn)升沉和縱搖輸出和加速度越小越好，本節(jié)提出具有優(yōu)化功能的垂向穩(wěn)定預(yù)測(cè)控制[13-14]。由上一節(jié)分析知道，海浪擾動(dòng)力和擾動(dòng)力矩均值都不為零，需要有積分作用來提高抑制海浪擾動(dòng)能力。因此，本節(jié)采用增量預(yù)測(cè)模型設(shè)計(jì)預(yù)測(cè)控制律。

Δx(k+1)=AdΔx(k)+BdΔu(k)+BwdΔd(k)

(8)

由于當(dāng)前k時(shí)刻的擾動(dòng)d是已知的，但未來時(shí)刻k+1，k+2…卻是未知并且不可測(cè)的，所以假設(shè)在k時(shí)刻之后的可測(cè)擾動(dòng)近似不變，即Δd(k+i)=0,i=1,2,…,Np。

對(duì)于系統(tǒng)的輸出y(k)，有

y(k+1)=y(k)+CdAdΔx(k)+

CdBdΔu(k)+CdBwdΔd(k)

(9)

將y(k)擴(kuò)展為一個(gè)新的狀態(tài)變量，擴(kuò)展后的狀態(tài)空間模型為

(10)

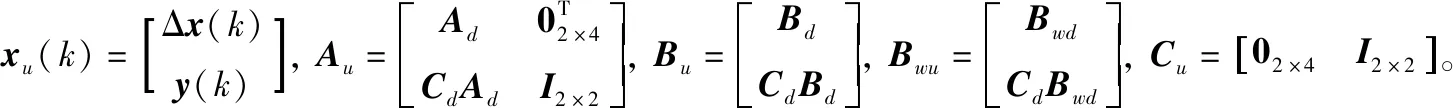
對(duì)k時(shí)刻，定義Np步預(yù)測(cè)輸出和Nc步控制輸入

YNp(k+1)=[y(k+1|k),y(k+2|k),…,y(k+Np|k))]T

ΔU(k)=[Δu(k),Δu(k+1),…,Δu(k+Nc-1)]T

則基于第k步系統(tǒng)狀態(tài)，未來k+Np步的預(yù)測(cè)輸出為

YNp(k+1)=Fxu(k)+ΘΔU(k)+GΔd(k)

(11)

式中，

高速多體船的垂向運(yùn)動(dòng)穩(wěn)定控制不僅局限于減少縱搖和升沉運(yùn)動(dòng)幅度，還需要減少縱搖和升沉的變化率，其原因是過大的縱搖和升沉變化率會(huì)引起多體船垂向加速度過大，進(jìn)而使得暈船率過大。這里將預(yù)測(cè)時(shí)域內(nèi)的縱搖和升沉變化率也引入優(yōu)化目標(biāo)函數(shù)，提出了下面的預(yù)測(cè)控制目標(biāo)函數(shù)

J=(Yref(k+1)-YNp(k+1))TQ(Yref(k+1)-

YNp(k+1))+ΔU(k)TRΔU(k)+

(YNp(k+1)-YNp(k))TK(YNp(k+1)-YNp(k))

(12)

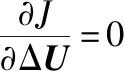
ΔU(k)=(ΘTQΘ+R+ΦTKΦ)-1[ΘTQ(Yref(k+1)-

Fxu(k)-GΔd(k))-ΦTK(Γxu(k)+ΨΔd(k))]

(13)

式中，

為了提高預(yù)測(cè)控制的魯棒性，只取ΔU(k)中的第一個(gè)元素作為實(shí)際的控制增量，在下一采樣時(shí)刻的控制增量根據(jù)下一采樣時(shí)刻的系統(tǒng)狀態(tài)重新計(jì)算。令矩陣H=[I2×20 … 0]，則當(dāng)前時(shí)刻的MPC控制量

Δu(k)=H(ΘTQΘ+R+ΦTKΦ)-1[ΘTQ(Yref(k+1)-

Fxu(k)-GΔd(k))-ΦTK(Γxu(k)+ΨΔd(k))]

(14)

為了驗(yàn)證上述閉環(huán)增量MPC的穩(wěn)定性，將增量MPC控制器方程式 (14) 代入系統(tǒng)方程式 (10) 可得

xu(k+1)=BuH(ΘTQΘ+R+ΦTKΦ)-1·

ΘTQYref(k+1)+(Au-BuH(ΘTQΘ+R+ΦTKΦ)-1·

(ΘTQF+ΦTKΓ))xu(k)+

(Bwu-BuH(ΘTQΘ+R+ΦTKΦ)-1·

(ΘTQG+ΦTKΨ))Δd(k)

(15)

閉環(huán)系統(tǒng)的穩(wěn)定性通過矩陣Au-BuH(ΘTQΘ+R+ΦTKΦ)-1(ΘTQF+ΦTKΓ)的特征值來判斷。當(dāng)加權(quán)矩陣為Q=diag(6.2×103，4.8×104)，R=diag(3.4×10-3，2.4×10-5)，K=diag(1.2×106，10×107)，計(jì)算可得6個(gè)特征值分別是0.963 7+0.138 4i，0.963 7-0.138 4i，0.976 7+0.067 5i，0.976 7-0.067 5i，0.995 2+0.000 0i，0.999 9+0.000 0i均位于單位圓內(nèi)，因此離散系統(tǒng)是閉環(huán)穩(wěn)定。

5 仿真分析

在仿真中高速多體船以兩體船為例，取采樣周期T=0.05 s，動(dòng)力學(xué)模型參數(shù)為[12]：

為驗(yàn)證增量預(yù)測(cè)控制減搖的有效性，采用四級(jí)海浪進(jìn)行仿真，仿真條件同文獻(xiàn)[9]，進(jìn)行下面仿真：

1) 分別對(duì)多體船進(jìn)行無控制器和增量預(yù)測(cè)控制的仿真，升沉位移和縱搖角圖5和圖6所示。無控時(shí)升沉位移均值為0.240 6 m，方差為0.089 1 m2，縱搖角均值為 0.736 3 deg，方差為0.014 6 deg2。在加入增量預(yù)測(cè)控制后，升沉位移均值為0.097 1 m，方差為0.015 4 m2，縱搖角均值為0.382 0 deg，方差為0.004 2 deg2。通過對(duì)比可以看出，在增量預(yù)測(cè)控制作用下多體船升沉位移減少了59%，縱搖角減少了47%，減搖控制效果明顯。

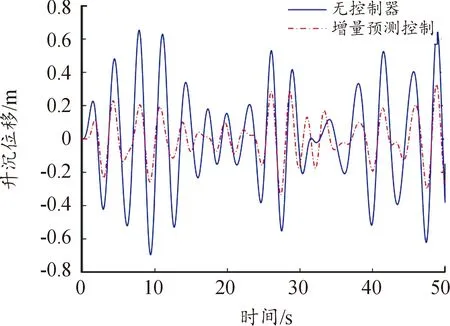
圖5 升沉運(yùn)動(dòng)Fig.5 Comparison of heave motion

圖6 縱搖運(yùn)動(dòng)Fig.6 Comparison of pitch angle motion

2) 為進(jìn)一步驗(yàn)證所提增量預(yù)測(cè)控制性能，與傳統(tǒng)預(yù)測(cè)控制減搖進(jìn)行比較[10]，結(jié)果如圖7和圖8所示，可以看出所提的預(yù)測(cè)控制使得升沉位移幅度進(jìn)一步減少16%，縱搖運(yùn)動(dòng)幅度減少約11%，波動(dòng)變化率明顯變緩，增強(qiáng)了多體船抑制海浪擾動(dòng)的能力。

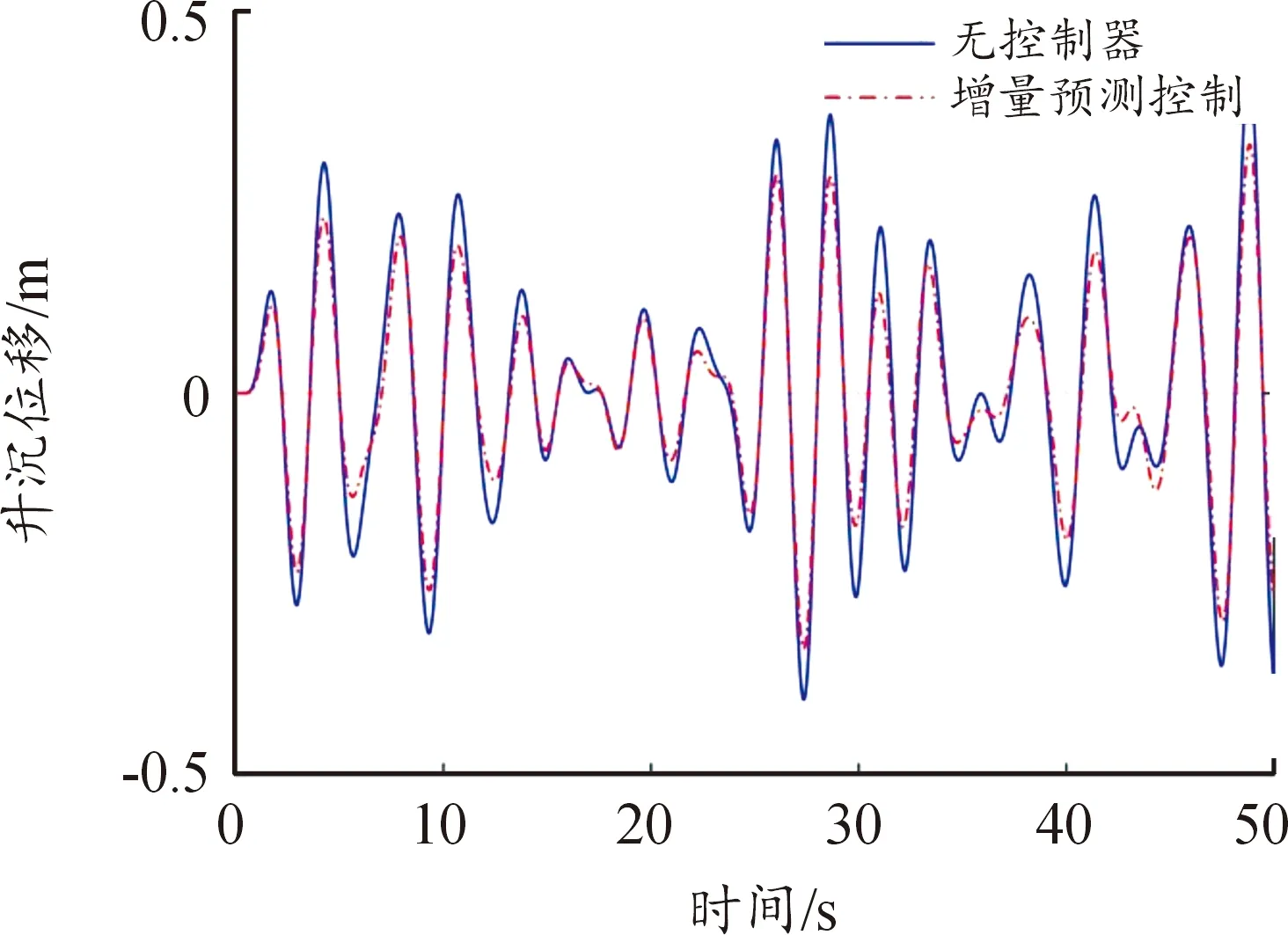
圖7 升沉運(yùn)動(dòng)Fig.7 Comparison of heave motion

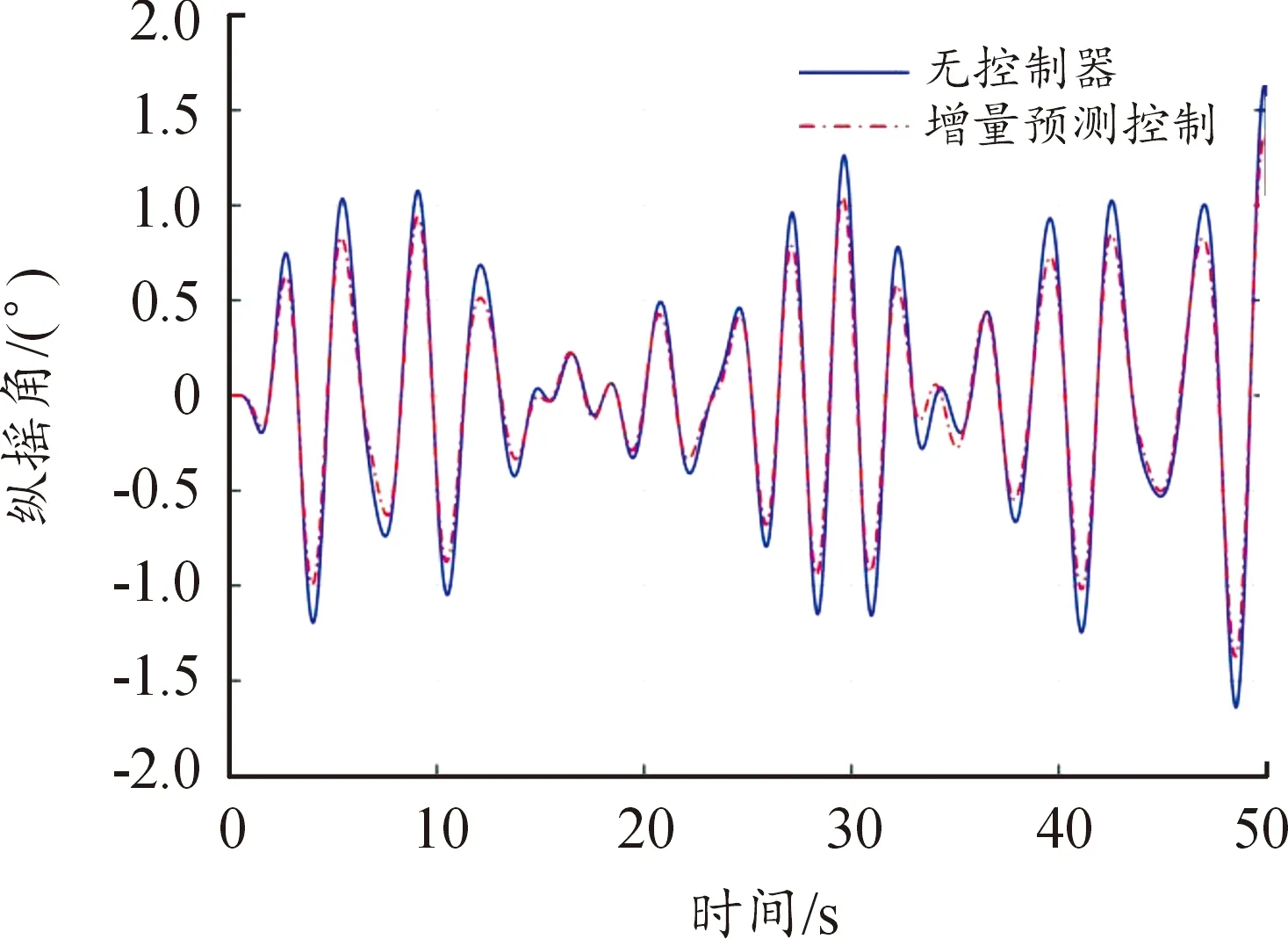
圖8 縱搖運(yùn)動(dòng)Fig.8 Comparison of pitch angle motion

6 結(jié)論

提出基于增量預(yù)測(cè)控制的高速多體船垂向運(yùn)動(dòng)穩(wěn)定方法，抑制過大的升沉和縱搖運(yùn)動(dòng)幅度。仿真結(jié)果表明：

1) 采用積分?jǐn)_動(dòng)模型在線估計(jì)海浪擾動(dòng)力和力矩，將估計(jì)值引入到預(yù)測(cè)模型中，增強(qiáng)多體船抑制海浪擾動(dòng)的能力。

2) 基于增量模型設(shè)計(jì)預(yù)測(cè)控制減搖方法，使得升沉位移減少59%，縱搖角減少47%。