三級子母彈分離方案氣動數值分析

初景江，李 盾

(中國航天空氣動力技術研究院，北京 100074)

1 引言

多級子母彈分離的空氣動力學問題，是一類典型的多體干擾、非定常復雜流動問題[1]。以機械式分離拋射為例，全過程大致可分為3個階段進行。第一階段，子母彈飛行過程中通常采用整流罩來保護部件免受氣動力、熱環境的影響，達到減阻的效果，到達一定高度和速度時需將整流罩拋離。子母彈有著飛行速度高、飛行高度低的特點，復雜的氣動力將使頭罩分離后的運動軌跡復雜，并可能與彈體相撞，導致災難性的后果。第二階段，導彈外層擋板在彈簧機構作用下以平沖的狀態離開母彈，之后受到干擾區流場的影響，產生復雜的氣動力，擋板的運動狀態受到氣動力的影響，需要設計合適的分離條件以保證擋板不與其他運動部件發生碰撞。第三階段，拋撒過程是子母彈武器系統的關鍵環節，子彈拋撒分離存在嚴重的子彈與母彈、整流罩、擋板間的氣動干擾，尤其是在超聲速飛行條件下的子母彈分離，往往伴隨著各運動部件間激波干擾，使得分離過程的流場結構異常復雜，可引起子彈及母彈氣動力不確定性，進而影響到子母彈的分離及毀傷效果。子母彈拋撒的各階段涉及到不同形式的多體分離問題同時又相互影響干擾，有必要對子母彈的多級分離全過程展開數值模擬。

國際上，美國率先開始了對于子母彈分離這一復雜流場的分析[2-4]。包括采用數值模擬與風洞試驗相結合的方法對子母彈氣動特性進行了研究[5];采用計算機程序精確模擬超聲速空腔中多個子彈彈體分離流場[6];采用非結構動網格方法、總變差不增有限體積法和并行計算技術對子母彈分離過程進行數值模擬[7]等,均取得與試驗結果符合較好的數值模擬結果。近年來，國內對子母彈分離流場特性的研究取得長足進展[8]。例如，對彈艙靠前和彈艙靠后2種子母彈結構進行了數值模擬[9]；討論出艙條件、氣動干擾和非定常效應等對分離運動的影響[10]；對時序拋撒方式下子彈在不同艙段分離的三維非定常流場進行了數值模擬[11]；對擾流板對子母彈翻轉角速度的影響進行研究[12]；對大口徑中心爆管式子母彈分離流場進行數值模擬[13]；對子母彈拋撒過程中氣囊破裂射流流場結構進行仿真分析[14-15]等。前人大多是對多級子母彈分離單過程展開詳細的數值模擬研究，默認開始子彈拋撒時之前拋離的整流罩與外層擋板已經遠離干擾區。但是拋開頭罩后導彈又飛行了一段時間，此時氣動外形提前發生改變，氣動系數改變，對子母彈原本規劃的運行軌跡會有一定影響。如何在短時間間隔內高效安全實現三級分離，便是本研究方案探討的目的。

三級多體分離相對單級多體分離而言，由于級間干擾的存在，除了很多共性問題以外，也有特性問題。子級部件大小、氣動結構外形、分離時的姿態、分離初始條件、部件質心位置以及各級分離時序等因素，均會影響到整個分離過程的成功與否。綜合過程不僅要保證各級分離單獨可行，還要保證三級分離全過程的安全高效進行。只有根據各因素的安全邊界進行適當調整設計，三級分離的方案在實際應用中方可實現。本研究針對虛擬模型的三級分離方案展開數值模擬，重點探討來流迎角、各級分離初始速度、蓋板氣動干擾對綜合過程的影響，并對設計方案的可行性與穩定性展開驗證。

2 數值方法

本次數值模擬所采用的課題組自研軟件，先前已對子母彈實驗以及頭罩分離等多體分離標模進行過驗證[16]，對單級分離過程如四體全自由飛[17]、低空高動壓整流罩分離[18]、拋撒投放分離、兩體級間分離的實際數值模擬說明，建立的數值模擬計算系統可以在一定程度上解決外形復雜的多體運動的實際工程問題。圖1為應用該軟件對全自由飛數值模擬結果與實驗數據的對比驗證。圖2為頭罩分離過程的數值仿真研究。

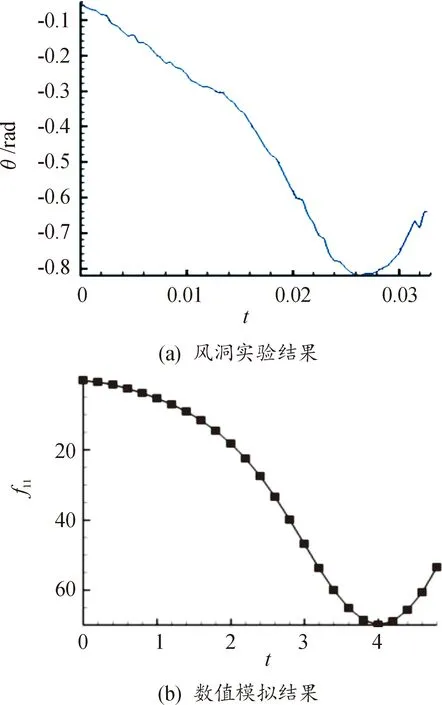
圖1 全自由飛前部俯仰角隨時間變化Fig.1 The change of the forward pitch angle in full free flight

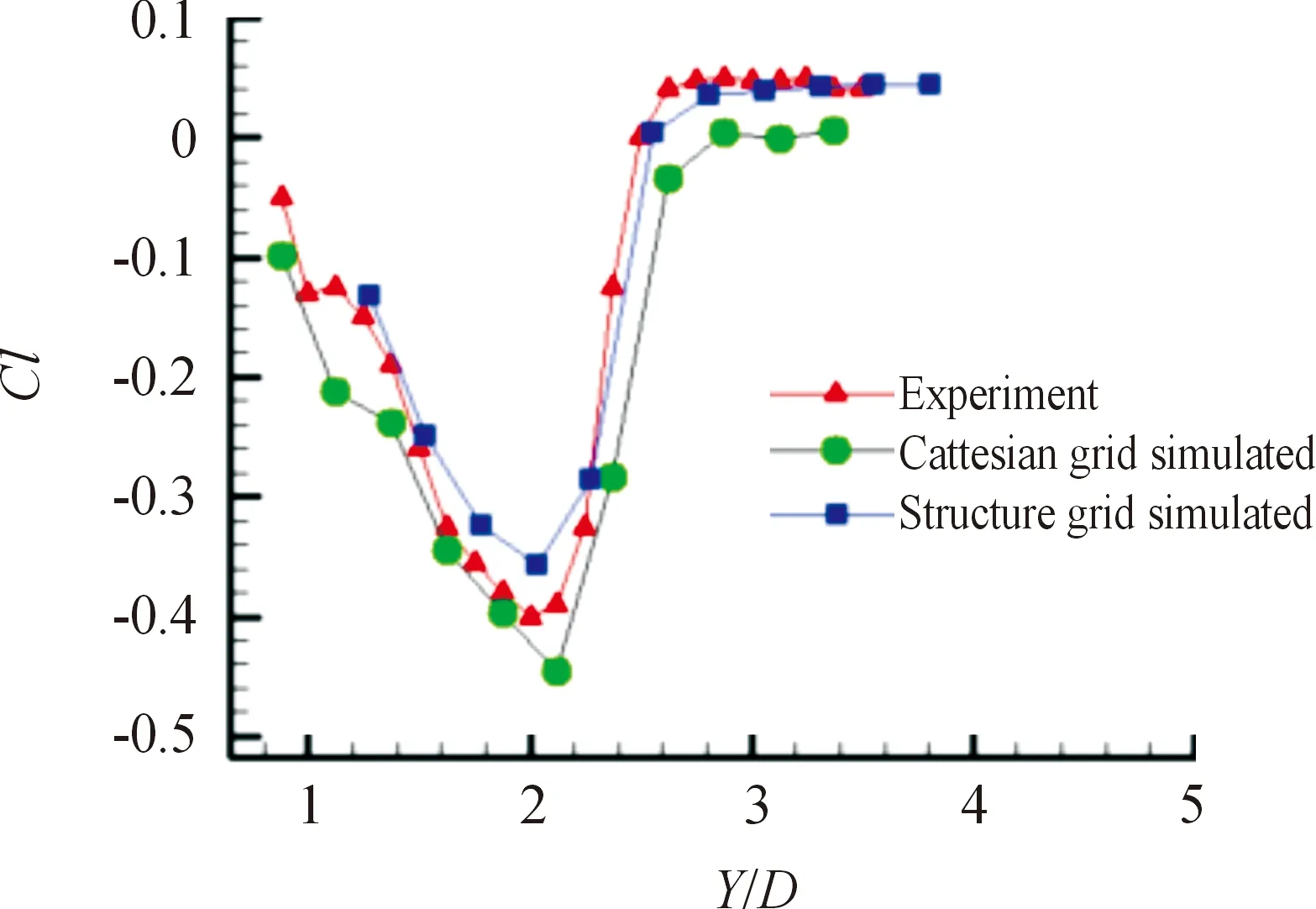
圖2 子彈穿越母彈激波分離數值計算與實驗對比Fig.2 Comparison between numerical calculation and the experiment for shock wave separation of a submissile passing through the mother shell

2.1 非結構直角網格技術

本文中數值計算網格，采用三維非結構粘性直角網格[19-21]重構的方法生成。其中主要包括兩大組成部分：三維非結構粘性直角網格的生成和運動過程的網格重構。由于整流罩拋罩、外層擋板拋離、子母彈拋撒3個過程按一定的時序設計先后進行，干擾區內同時存在多個運動部件，流場物面外形復雜且時空間尺度差異較大，采用非結構網格可以更準確地對物體復雜的幾何外形進行描述。直角網格具有生成簡單、流動求解器容易實現等優點，同時采用局部網格加密技術提高邊界附近流場的計算精度。運動物體小位移采用彈性網格變形技術，大位移直接進行網格重構。由此生成的三維非結構貼體直角網格，可以適應各種復雜外形的黏性流與湍流的計算。

2.2 ALE形式控制方程、6DOF運動方程耦合

多體分離問題是典型的動態問題，在發展針對此類問題的數值方法時，需要考慮如何捕捉運動邊界。使用任意拉格朗日-歐拉形式控制方程對流場進行描述，由牛頓基本定律結合慣性/非慣性坐標系轉換推得六自由度彈道方程。

耦合方法：基于當前步網格、流場，凍結各運動物體的位置姿態，求解流動控制方程，得到時間方向推進后的下一時間步的流場，積分得到運動物體受到的氣動力和力矩；根據n時刻物體的位置姿態，凍結運動物體的受力，求解剛體運動方程，獲得時間步內物體位置和姿態的改變量；根據物體新的位置姿態，采用動網格技術獲得n+1時刻的計算網格；完成n時間步的計算，開始n+1時刻的計算。

2.3 時空間離散方法

有限體積法對網格類型、網格質量要求不高，適合于復雜外形、復雜運動過程繞流的計算，在多體分離問題模擬中應用較為廣泛，本研究主要采用基于格心的ALE控制方程有限體積離散方法。

空間離散方面，采用有限體積法對流動控制方程進行空間半離散。

(1)

對于任意網格單元，M表示單元面的數目；W表示單元第i個面的面積向量；Fs和Fvs中的下標s表示變量取單元面上的值。這里粘性通量可采用中心差分求解，對流通量可以采用各種通量計算格式，但由于ALE流動控制方程中考慮了網格速度Vb的影響，因此通量格式中也需要相應的計及網格速度，如考慮了單元面運動的Roe格式。

計算對流通量時，迎風格式采用MUSCL線性重構技術以獲得二階精度，并采用Venkatakrishnan、Barth等限制器以抑制較大流動梯度區域出現振蕩，由此可實現超聲速彈體流場激波的精確捕捉。研究重點關注物體間分離運動且分離相對速度較小，湍流對此過程影響較小，考慮到計算效率問題，并未引入湍流模型。

時間離散方面，雙時間步方法通過引入虛擬時間步，將因為穩定性條件對時間的限制轉移到虛擬時間步內，物理時間上允許的時間步長將有條件地放寬。對流動控制方程進行空間離散，得到半離散型方程：

(2)

式中，Ri表示單元i各單元面無粘通量與粘性通量的積分。此半離散式中包含瞬態項，能完整描述流動隨時間的變化。當采用雙時間步方法模擬非定常流動時，需要在方程中引入虛擬時間項：

(3)

這里用τ表示虛擬時間。對虛擬時間步采用一階歐拉隱式離散，物理時間步采用k階隱式離散，離散后的通用表達形式為：

(4)

3 子母彈分離過程的數值模擬

3.1 子母彈模型

子母彈的幾何模型如圖3所示。該子母彈由彈體、整流罩、子彈以及外層擋板四大部分組成。本研究主要針對子母彈拋撒過程中各分離部件展開數值模擬，子母彈的其余組成部件暫且不在模型中細致的表現出來。

圖3 子母彈網格模型及內部結構展示Fig.3 The mesh of a submissile model and its internal structure

模型中各部件質量屬性設計如下：設計子母彈總質量400 kg，長度為2.14 m，直徑0.4 m，彈倉長度0.8 m。整流罩與外層擋板分別重4.7 kg和12.7 kg，質量均勻分布。子彈長度0.66 m，直徑0.07 m，質量5 kg，4枚子彈等間距分布于彈艙內。多級分離時，在保證各分離部件不碰撞的情況下，整流罩及外層擋板的穩定性可以不予考慮，但子彈及子母彈整體的分離穩定性問題需要單獨進行設計，也即分離過程中質心位置的選取。經過后續的數值模擬發現，子彈質心選取在距頭部三分之一彈體長度處可保證多級分離全過程子彈與母彈的飛行穩定性。

由于各分離部件相對母彈而言尺度較小且成軸對稱排布，在初期分離的較短時間內母彈狀態變化不大，因而可以鎖定母彈的自由度進行研究，由此產生的微小誤差在可承受范圍內。

3.2 子母彈運行工況、分離時序設計

假設子母彈飛行至作戰區域后，在海拔高度4 km處以1.5馬赫速度進行三級分離運動，進行來流條件設置。三級分離時不僅存在著各部件間的氣動干擾，還存在著分離時序干擾問題。設計了以下一種分離方案：整流罩張開至45°時開始進行拋罩；拋罩分離進行至20 ms時，開始進行外層擋板的拋離；外層擋板開始拋離30 ms后，子彈在彈簧機構作用下以一定的初始速度拋出。

3.3 計算域設置及網格生成

多階段分離時，由于各分離部件分離時間點不一致，會導致分離干擾涉及的空域較大。例如當第三階段子彈開始進行拋撒時，第一階段分離的整流罩已經拋出很遠的距離。為了能夠在分離初期對各個分離部件進行持續的數值模擬，計算域也需設置較大。

規定好計算域，對計算域進行初步的網格尺度劃分。在表面網格的基礎上按照直角網格生成與重構方法，采用三維非結構粘性直角網格技術對導彈進行計算域內的網格生成。仿真過程中，彈艙內子彈、頭部整流罩以及彈艙處的外層擋板為運動部件，需要重點分析運動部件周圍的流場信息，因此對這些部件周圍流場網格進行加密設置。

4 多級分離方案可行性分析

針對上述模型，調整來流迎角與各級分離的初始速度，對設計方案的可行性與穩定性展開研究，探討單因素對綜合過程的影響。對單獨進行子彈拋撒及三階段連續進行2種分離狀況數值模擬，研究頭罩擋板對子彈的氣動干擾，說明展開多級研究的必要性。

當自由來流攻角為0°時，對前述時序設計的適用性展開研究。對每一個分離階段單獨進行數值模擬發現：第一級分離的頭罩在多數分離姿態下均可保證分離安全性；二級擋板以小于16 m/s初始速度平拋或三級子彈以小于12 m/s速度拋出時，在擋板及母彈的流場干擾作用下，擋板及子彈拋離后與母彈尾翼有發生碰撞的危險；當子彈初始分離速度大于擋板時，兩側子彈與先前拋離的外層擋板有發生碰撞的危險。因此，對于該時序方案而言，需要嚴格設計各級分離的初始分離狀態，才能保證方案總體可行，其中第二級與第三級分離應是研究重點。

圖4是標準設計狀態下，來流迎角0°、擋板平拋初始分離速度V1=20 m/s、子彈拋撒初始分離速度V2=20 m/s時，對該多級分離方案的數值模擬。仿真結果進一步說明該設計方案的可行性，同時也符合短時間內實現三級分離的設計要求。在短時間內完成三級分離，多體干擾區內同時存在著整流罩、外層擋板、子彈以及母彈等多個運動部件，彼此間的相互干擾嚴重，激波在各運動部件間反射交錯，流場復雜。觀察流場信息圖可知，整流罩在開始分離50 ms后基本飛離干擾區；外層擋板100 ms時已基本不再對后續的子彈拋撒產生作用；子彈在全過程分離開始90 ms后，即開始子彈拋撒40 ms后開始穿越母彈彈體激波層。后文將圍繞該特定方案，調整其他參數，通過獨立研究各分離因素對綜合過程的影響，進一步確立可行方案。

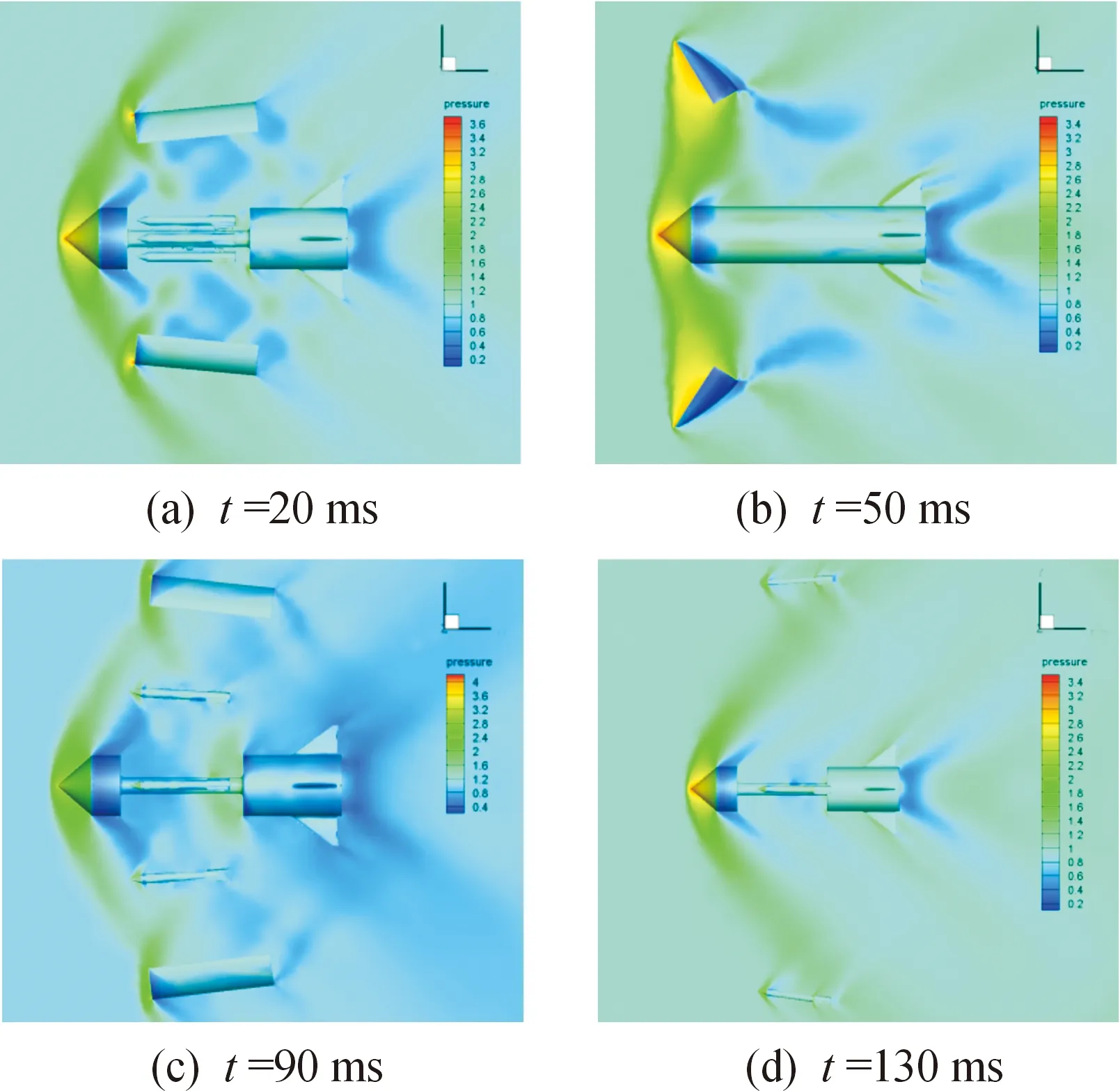
圖4 多級分離數值模擬結果Fig.4 Numerical simulation results of multistage separation

4.1 分離姿態對方案可行性的影響

設計擋板初始分離速度V1=20 m/s,子彈初始分離速度V2=16 m/s，改變自由來流的迎角，研究設計方案在大迎角狀態的分離可行性。分別對來流迎角為0°、5°、10°三種情況數值模擬，以下方子彈為例分析。圖5所示為子彈分離 100 ms，俯仰角隨分離時間變化。情況1、2、3分別代表來流迎角為0°、5°、10°的分離姿態。按照方案設計，質心位置大部分時期處于壓心前方，保證了子彈拋撒后的動態穩定性。子彈穿越母彈激波過程中，壓縮氣流首先作用于彈體前端，導致短暫的失穩狀態，在這20～30 ms期間壓心逐漸移至質心之后，子彈快速恢復飛行穩定性。由三維仿真圖像可知，雖然該過程子彈俯仰角產生較大變化，但仍可保證三級分離的安全進行。由圖5可知，設計方案應盡量保證在來流迎角較小的情況下進行子彈拋撒，來流迎角10°時俯仰角上下波動約30°，說明大迎角可能會導致短時間的失穩狀態擴大化，不利于子彈保持穩定狀態下的安全分離。

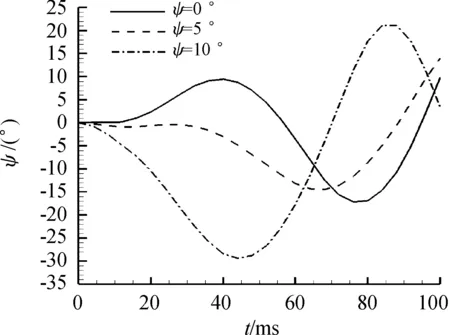
圖5 3種來流迎角下子彈俯仰角變化Fig.5 Variation of the bullet pitch angle under three angles of attack

4.2 擋板及子彈分離速度對方案可行性的影響

第二級分離時擋板的平拋速度V1以及第三級分離時子彈的拋撒速度V2，是影響綜合過程是否安全穩定的重要因素。圖6所示為5種分離條件下，子彈受母彈與擋板激波層共同作用時，穿越激波過程中力矩的變化。圖中M1代表上方子彈俯仰力矩，M2代表下方子彈俯仰力矩，M3、M4代表左右兩側子彈的偏航力矩。4種力矩均是對子彈分離后運動穩定性的考量，若能夠保持穩定，則證明在設計的分離速度下該方案可行。

子彈穿越激波過程，受到母彈與外層擋板激波層的共同作用，根據圖6對該過程子彈受力狀況展開分析。首先母彈激波層作用于子彈前半部分，附加彈頭向外偏轉力矩，此時壓心位置位于質心前方，子彈處于短暫的失穩狀態；隨著拋離過程的進行，壓心不斷后移，20～30 ms后激波層作用于子彈后半部分，子彈快速恢復運動穩定，同時激波附加彈頭向內偏轉力矩，原本外張的姿態角開始向內靠攏，直至完全穿越母彈激波層。通過子彈質心位置的設計，可使子彈拋離后總體上維持運動穩定。三維仿真結果顯示，對于圖6提出的五種分離方案，子彈拋撒過程雖有短暫的失穩狀態出現，并伴隨較大的俯仰力矩變化，但不會影響到分離方案的可行性與整體穩定性。

對比圖6中(a)(b)(c) 3種情況，固定子彈拋撒初速度的情況下，適當增大擋板平拋速度V1，可以有效防止第三級拋出子彈與第二級拋出擋板間發生碰撞，但子彈拋離后穿越激波過程中所受的力矩變化較大，穩定性稍差。對比圖6中(a)(d)(e)三幅圖片，隨著子彈初始分離速度V2增大，穿越激波過程的左右兩側子彈偏航力矩變化也在隨之增大，即側方位子彈分離后會產生更大的姿態角偏轉。綜上，方案設計應在安全分離的前提下保證V1與V2盡可能小，有利于分離后子彈的穩定飛行。

圖6 子彈力矩變化Fig.6 Change of bullet moment

4.3 2種情況子彈拋撒對比分析

對單獨進行子彈拋撒與三級分離連續進行2種情況展開數值模擬。多階段分離由于發生在較短時間內，前一個階段的分離運動導致的流場變化對后續階段的分離狀態都會產生較大影響。由于擋板側向分離，因此這種影響對于側面兩枚子彈最為明顯。以XY平面內的一枚子彈為研究對象，對2種分離狀況中子彈拋撒這一重點環節對比，探討整流罩、蓋板對子彈拋撒時運動姿態的具體影響和作用機理。

圖7、圖8所示為2種情況子彈拋撒時，側方位子彈質心位置以及偏航角隨時間變化情況。情況1代表單獨進行子彈拋撒，情況2代表三級分離連續進行。由圖7可知，該模型在子彈拋撒的初段時間內，情況1與情況2子彈分離速度相當，均可保證方案安全可靠。圖8顯示，2種分離情況的差異主要體現在姿態角的變化上，情況1子彈的偏航角略大于情況2，這也與先前數值模擬結果相吻合。結合圖9力矩變化以及前文流場圖像可知，之所以出現2種分離情況子彈偏航角相差較大的現象，是因為情況2中上一步分離的外層擋板仍在干擾區內，子彈在分離初始仍受到擋板激波的作用，作用于子彈的前半部分，附加彈頭內向偏轉的偏航力矩，抑制偏航角的持續增大。由此也可看出，外層擋板的存在減小了子彈分離時的力矩變化，有利于其保持相對穩定的分離狀態。

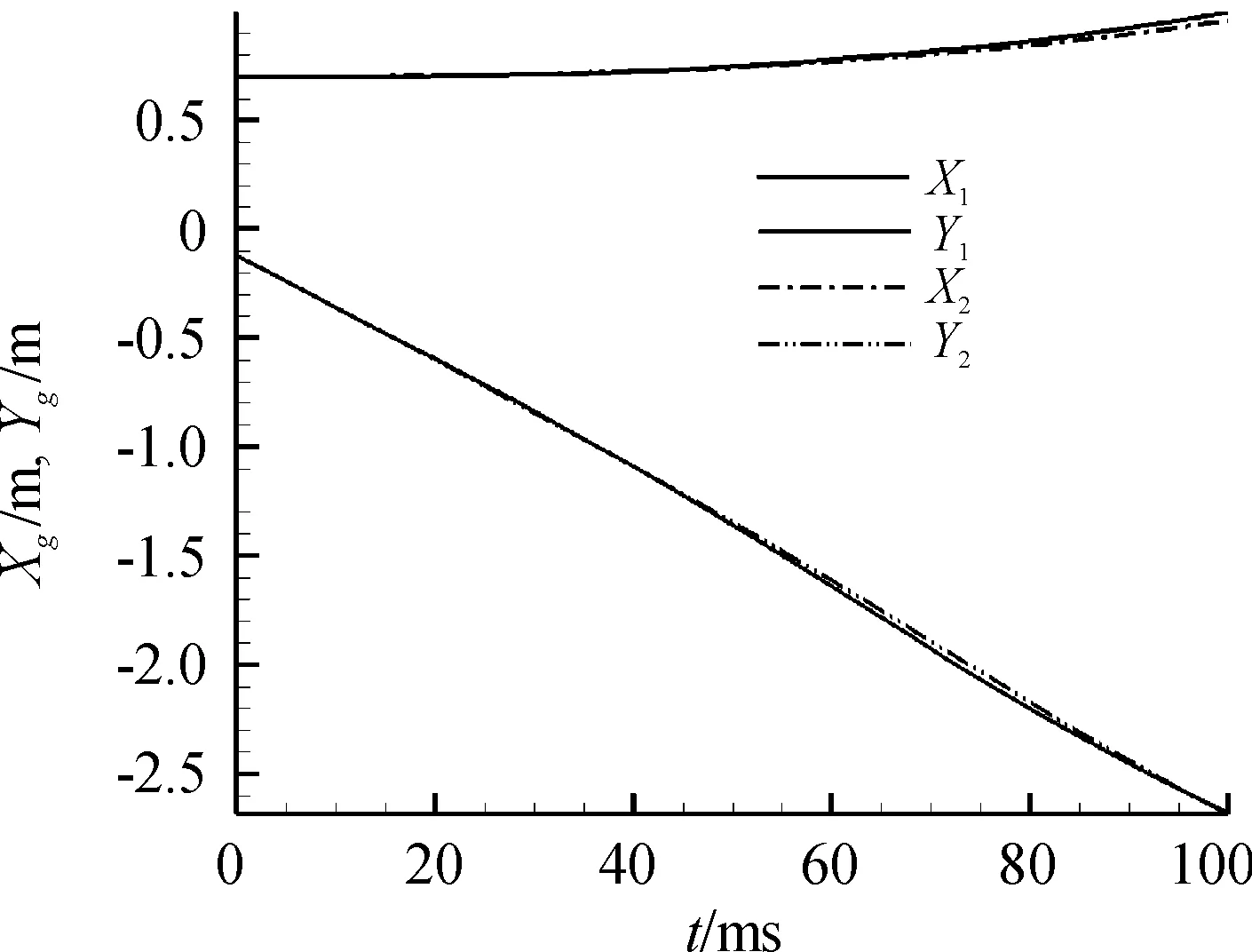
圖7 2種情況子彈拋撒質心位置隨時間變化Fig.7 The change of the position of the mass center vs.time under two situations

圖8 2種情況姿態角隨時間變化Fig.8 The change of the attitude angle vs.time

圖9 子彈力矩隨時間變化Fig.9 The change of the moment vs.time

5 結論

綜合了頭罩拋離、外殼分離、子母彈拋撒三類現有的分離物理問題，虛擬了一個模型，對該模型三級分離展開氣動數值模擬，研究了三級分離過程中的一些共性問題和特性問題。重點對分離姿態、各子級初始分離速度以及擋板干擾3個影響因素展開研究，結果顯示：

1) 改變三級分離姿態角，發現大迎角可能會導致短時間的失穩狀態擴大化，不利于子彈分離時的穩定性。

2) 調整擋板及子彈初始分離速度，研究分離方案的可行性與穩定性，提出了幾種具體可行的速度優化方案。

3) 干擾區內頭罩拋離及擋板平拋對后續子彈拋撒有影響，擋板的存在減小了子彈分離時姿態角變化，有利于其保持相對穩定的分離狀態。

4) 合理控制分離姿態、各子級初始分離速度以及擋板干擾，可以實現三級安全分離。