“數學文化情境試題”課堂教學實踐
——以“數學文化之旅——空間圖形體積問題”教學為例

2023-03-01 09:12:26江蘇省常州高級中學213003

中學數學月刊 2023年2期

陳振 (江蘇省常州高級中學 213003)

數學文化是指數學的思想、精神、語言、方法、觀點以及它們的形成和發展，還包括數學在人類生活、科學技術、社會發展中的貢獻和意義，以及與數學相關的人文活動．《普通高中數學課程標準(2017版)》[1]指出：數學文化應融入數學教學活動．教育部考試中心頒布的2017年高考數學考試大綱增加了對“數學文化”的考查，這使得數學文化素養對我們而言愈加重要．為順應時代要求，努力達成課標要求，筆者嘗試進行數學文化情境試題探究，并據此開設了本校的校慶公開課．通過查閱近年來各地高考模考試卷，決定以“空間圖形體積問題”這一微切口展開嘗試，和學生一起探討、研究數學文化情境試題．本課題面向高三一輪復習的學生，學生已經具備完整的高中數學知識，且對數學文化試題有了一定的了解．下面將結合本節課教學設計作一些分析與反思．

1 教學設計

1.1 基礎鞏固——讀圖

縱觀數學的歷史，“形”的意識也許跟人類歷史一樣古老．中國的幾何有著悠久的歷史，據可靠記載，在中國出土的新石器時代的陶器大多為規則形狀，陶器上有各種幾何圖案，通常還有三個著地點，這些都是幾何知識的萌芽(圖1)．

圖1

設計意圖精美圖片展示我國古人的幾何智慧，激發學生探索幾何圖形的興趣．

接著，選取其中的一個紫砂壺為情境作為例1．

例1紫砂壺是中國特有的手工制造陶土工藝品，紫砂壺的壺型眾多，經典的有西施壺、掇球壺、石瓢壺、潘壺等．圖2給出了一個石瓢壺的相關數據(單位：cm)，則該壺的容量約為( )．

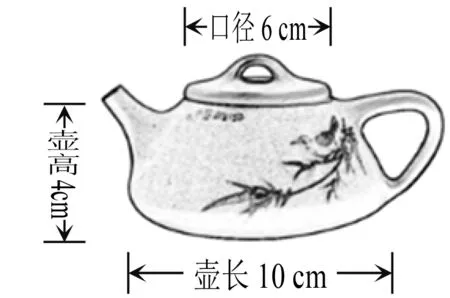
圖2

A.100 cm3B.200 cm3

C.300 cm3D.400 cm3

設計意圖在呈現問題時，筆者有意將原題中的一關鍵條件——“壺體近似看成一個圓臺”隱去，而這一條件學生是可以通過圖形得到的，重點關注讀圖能力的培養．同時，隱去條件后，本題就是一道有開放性意味的情境問題．學生可以解讀成圓臺，也可以看成是其他幾何體．

真實課堂中有學生將壺體當作圓柱，這當然是不合理的，引導學生再讀圖去發現，壺長和口徑長不同，不符合圓柱的特征．筆者順勢和學生一起復習圓柱、圓錐、圓臺的幾何特征，鞏固立體幾何圖形基本知識．也有學生將壺體看成是球體的一部分，但在計算容量時學生自然會發現，近似看成球體后，由于球體的半徑不明確，體積的求解難以實現，本道例題還是視作圓臺更合適．筆者也鼓勵學生在課后查閱資料，進一步完善球體計算這一想法，達成自主探究目標．這些都是有意義的課堂生成.通過和學生一起讀圖分析，向其傳遞一個信息：重視讀圖．通過讀圖，一般可以獲得一些有效信息．同時，讀圖要有問題意識，帶著問題閱讀圖形，將研究圖形本身的特征與關注題目要解決的問題有機融合．

補全題目后，引導學生將相關數據與圖形結合起來，并在圖中標注好，謹防出現數與形不對應．去掉情境，題目為：已知一圓臺，上底面半徑是3，下底面半徑是5，高是4，求壺的容量，即是求圓臺的體積．此時學生依然有不同的選擇：直接運用圓臺的體積公式，或是利用大圓錐減小圓錐．筆者又和學生一起復習基本幾何體的體積公式．最后，這道題目還涉及估算，學生若能將π近似為3，計算將得到簡化，既節約了時間又提高了正確率．

這道題目由課堂情境導入，自然順暢產生，文字敘述也簡潔凝練．題目雖簡單卻涉及多個知識點，涵蓋了立體圖形的幾何特征、體積公式等解決“空間圖形體積問題”的必備知識．同時初步滲透讀圖、作圖、用圖的思想，培養去情境化、建立模型的意識．能讀圖，依據問題意識讀出有效的圖形，是問題解決的前提．

1.2 能力提升——作圖

我們的古人在生產生活實踐中也產生了很多圖形問題，發展出很多求解幾何體體積的方法．《九章算術》是我國古代的數學巨著，對于中國和東方數學，大體相當于《幾何原本》對于希臘和歐洲數學．其卷第五“商功”章主要討論空間幾何體體積求解問題，從中選擇一道作為例2讓學生都來解一解．

例2《九章算術》是我國古代的數學巨著，其卷第五“商功”章有如下的問題：“今有芻甍(chú ménɡ)，下廣三丈，袤四丈，上袤二丈，無廣，高一丈．問積幾何？”意為：“今有底面為矩形的屋脊形狀的多面體(圖3)，下底面寬3丈，長4丈，上棱2丈．上棱平行于下底面且與下底面的距離為1丈”，則它的體積是立方丈．

圖3

設計意圖例2依然是一道具體情境下的空間幾何圖形的體積問題．呈現題目時，也刻意隱藏了原題中的數學圖形，而換成了一張生活實景圖．需要學生依據剛剛的解題經驗，通過閱讀題目，自己作圖，抽象出相應的幾何體．

筆者通過課堂觀察，發現學生基本都能讀懂題意并作出圖形．但作圖依然存在兩類問題：一是虛實線不分，導致空間圖形立體感不強；二是方位不對，空間的點線面位置關系不清晰．這些圖形正確卻不很合理，不符合立體圖形的審美要求，不利于解題．在平面中展示立體圖形，是一個難點，需引導學生慢慢體會與感悟．

此時，我們已經可以將這道問題的情境過濾，用數學語言描述問題．

例2今有底面為矩形的屋脊形狀的多面體(圖4)，下底面寬AD=3丈，長AB=4丈，上棱EF=2丈，EF∥平面ABCD．EF與平面ABCD的距離為1丈，則它的體積是立方丈．

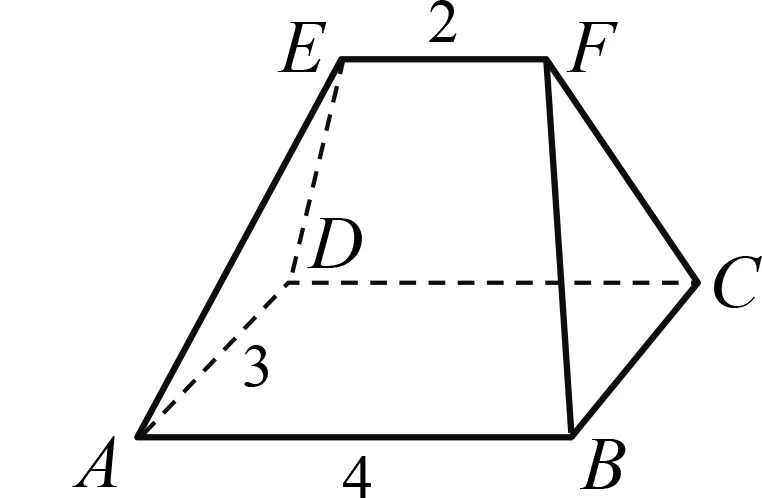
圖4

筆者追問：“這是什么幾何體呢？”引導學生發現這是一個一般的空間五面體，并不是我們熟悉的柱錐臺，不能直接運用體積公式．那怎么辦呢？學生大多會想到割補的思想．筆者適時給予鼓勵：這和我們古代數學家的想法是一致的！順勢介紹《九章算術注》，劉徽在書中全面論證了諸多幾何體體積公式，并發展了出入相補原理、截面積原理、齊同原理等．其中出入相補原理是：一個立體圖形被分割成若干部分后，體積的總和保持不變．佐證學生的想法，鼓勵學生進一步探究到底．

利用割補的方法，大多數學生都能夠順利解決問題．但也有人在解題時直接將EF擺在中間的位置，默認幾何體兩側面對稱，簡化了運算，得到的結果也是一樣的．此時，課堂生成了新問題：“本道題將幾何體特殊化求體積，可以嗎？”學生會有不同的意見與想法，待他們充分表達后，筆者展示事先準備好的GGB動畫，通過直觀觀察發現，改變EF位置，幾何體在所有等高處的截面面積保持不變．利用祖暅原理，即可確定體積不發生改變．因此，本題將幾何體特殊化來求體積是可行的．

順勢向學生介紹祖暅原理[2]．祖暅用這一方法，證明了球體體積的計算問題．我國古代數學家在極限思想的運用上遠遠超過了同期其他國家的同類思想，達到了文藝復興前世界數學界的最高峰．民族自豪感油然而生！

這道例題由《九章算術》而來，富含文化底蘊．其難度較例1有所提升，學生要通過讀題準確作出圖形，求解體積的方法也不再是簡單地套用公式，強化滲透讀圖、作圖、用圖的思想，培養去情境化、建立模型的意識．會作圖，把握重要因素，準確作出圖形，是問題解決的關鍵．

1.3 知識遷移——用圖

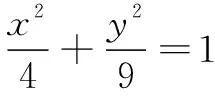
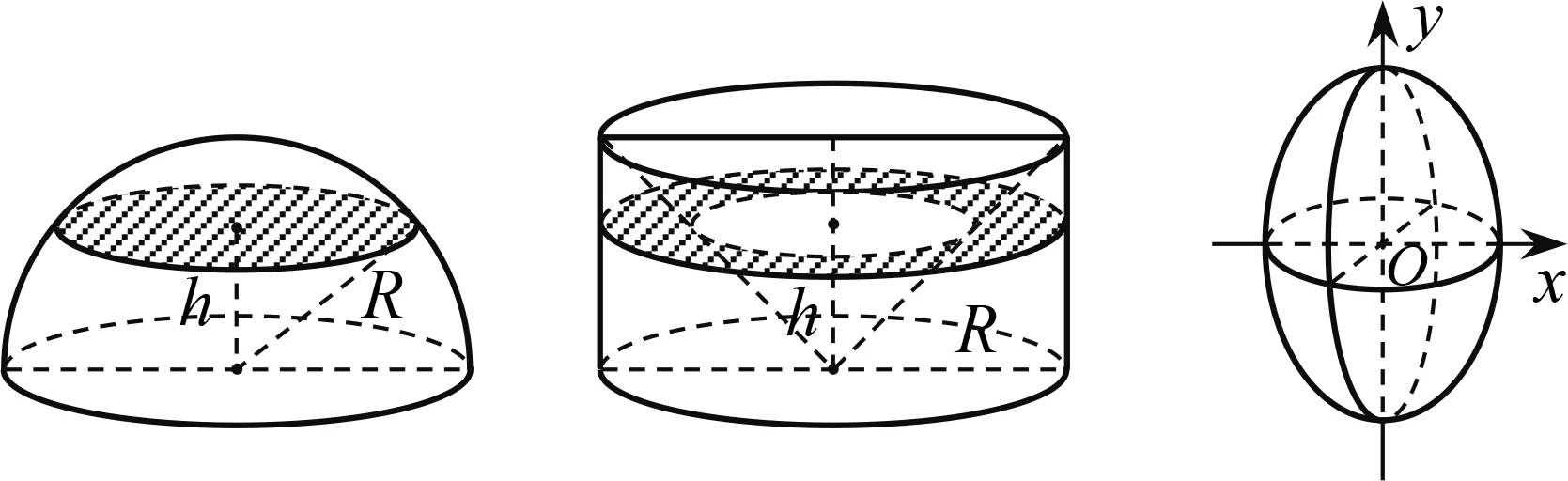
圖5 圖6 圖7

A.4π B.8π C.16π D.20π

設計意圖以祖暅原理為情境背景的題目有不少，筆者選擇的這道例題需要學生先類比作出與要求幾何體等體積的基本幾何體再進行體積求解．這是一個難點，需要學生真正理解祖暅原理，并讀懂、用好題目中的橄欖狀的幾何體．本題有一定思維度，為了讓學生真正掌握祖暅原理的本質而非限于解決題目本身，鼓勵學生進行小組討論并將討論結果在班級展示．

這道例題不再是考查學生用已經掌握的基本方法去求空間幾何體體積，而是在創設的情境中給學生提供思路，讓學生直接應用到體積的求解中，對思維的要求是更上一個層次的．因此，筆者鼓勵學生合作學習，通過組內討論和小組分享，讓所有學生參與其中，集眾人智慧解決問題．這既不會讓部分學生望“題”興嘆，又達到了思維訓練的難度．學生的表現也很亮眼，不僅順利建立了等體積的模型，而且通過計算論證了截面面積保持相等，嚴謹證實了模型的合理性，令人驚喜.

這道例題的情境既是背景又是工具．祖暅原理是教材中的閱讀材料，但絕非晦澀難懂，放在情境中，既達到了深層次的考查目標也不會超綱．同時，進一步滲透讀圖、作圖、用圖的思想，培養去情境化、建立模型的意識．會用圖，抓住關鍵特征用好圖形，是問題解決的難點．

2 教學反思

近幾年高考，以數學文化為背景的空間幾何體體積問題層出不窮，讓人耳目一新，同時，它也讓我們受困于背景陌生，閱讀受阻，思路無法打開．為了嘗試改變這一局面，筆者設計了這節課，選用的大體是兩類情境：作為素材背景顯性呈現的情境，主要是例1、例2，例1復習了空間幾何體基本幾何特征、基礎體積公式，例2滲透了割補的基本方法；以及作為思想方法隱形呈現的情境，主要是例3，運用“文化”蘊含的數學思想和數學方法進行數學解題，將祖暅原理應用于體積求解．力求為學生滲透讀圖、作圖、用圖的思想，培養去情境化、建立模型的意識．