核心素養下培養動態思維力是數學育人的抓手*

朱文平 (重慶市銅梁一中 402560)

眾所周知，數學是關于思維的科學，數學獨特的育人功能主要體現在培養學生的思維力，特別是要讓學生學會邏輯性思考、批判性思考、創造性思考．實踐證明：數學思維是高中數學六大核心素養的靈魂和至高點．因此，引導學生從“學會”到“學會學”，培養“思維力”是提高數學教學質量的基石和育人的根本任務．下面以幾個具體的例子來闡明培養學生的深層思維的路徑：自省→反思→調整→再思考→素養達成．這為學生今后學習習慣的養成奠定堅實的基礎，真正有利于聚焦學生核心素養的生成．

1 案例展示

例1在△ABC中，角A,B,C的對邊分別是a,b,c，若a+c=4，2sinB=sinA+sinC，則△ABC面積的最大值為( )．

教師留3分鐘給學生思考，讓學生自己讀題、審題、畫圖、思考，充分暴露“思維的障礙點”．接下來，由2～3位學生談談他們的想法．

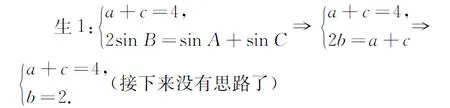
師：思考一下，面積中可以涉及角的正弦，接下來可否考慮用正弦或余弦定理來解決呢？

師：要求面積的范圍，關鍵是先求角B的范圍.同學們再思考，還什么條件可挖掘？

(學生自覺展開熱烈的討論)

師：接下來怎么辦呢？關鍵還得求出角B的取值范圍．請同學們思考一下，還有什么條件沒有挖掘出來呢？

師：同學們，還有其他解法嗎？(學生沉默)

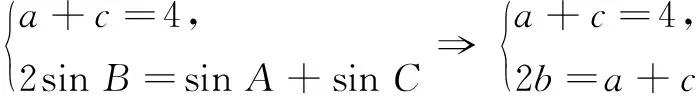
圖1

點評思維是解決問題的基石，只有在解決具體問題中教思維、教體驗、教表達，才能潛移默化聚焦學生良好思維品質的生成．

例2(2014年全國I卷第16題)在△ABC中，角A,B,C的對邊分別是a,b,c，若a=2，(2+b)(sinA-sinB)=(c-b)sinC，則△ABC面積的最大值為．

教師可引導學生先閱讀、理解、思考、解決問題，重在思維分析能力培養．

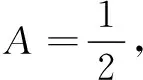
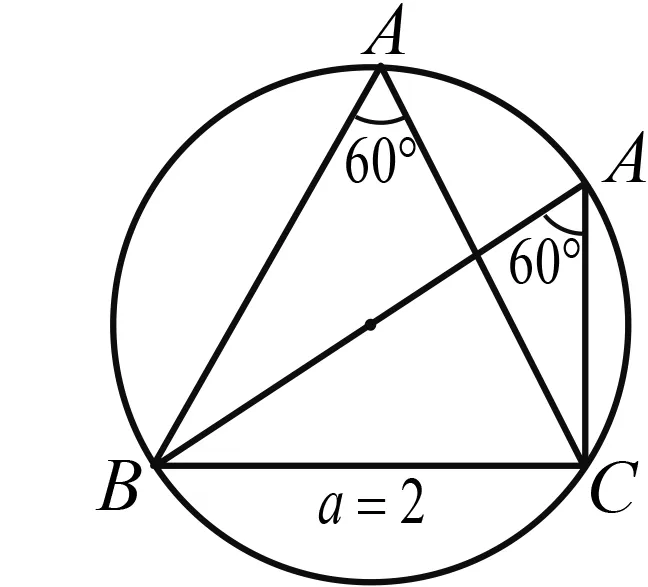
圖2

師：思考1，其他條件不變，求△ABC的面積的取值范圍；思考2，若△ABC為銳角三角形，其他條件不變，求△ABC的面積的取值范圍．

例3在△ABC中，角A,B,C的對邊分別是a,b,c，已知acosB=bcosA，邊BC上的中線長為4，則△ABC面積的最大值為．

生1：acosB=bcosA?sinAcosB?sinBcosA?

sin(A-B)=0?A=B.又因為邊BC上的中線長為4……接下來怎么辦呢？

圖3

師：同學們，生2的解法對嗎？其實角C的范圍又是多少呢？還有其他方法嗎？(學生探討)

點評在思維的“障礙點”處，教師起的關鍵作用就在于“引路”．其實這時候可以將問題進行延伸和拓展．

2 引申

引申 已知A,B是平面上的兩個定點，C為平面上的一個動點，若滿足AB=m，AC=λBC(λ≠1)，則C的軌跡為圓(即阿波羅尼斯圓)．

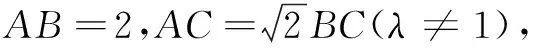
有了引申和例4的啟發，于是：

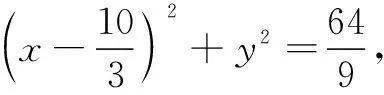
圖4

點評通過最后教師的點撥，發現生2的答案是錯誤的．其思維的難點在于角C的范圍是什么太難找了．教師重在教“活”，其本質還是圍繞“思維”教學．同時，“形數結合”彰顯了數學直觀想象的無窮魅力．

3 結束語

數學課堂應該基于“思維”教，圍繞“思維”學．作為教師，應挖掘數學教學內容中的思維價值，盡 可能在每一節課中設計有利于放大這些思維價值的數學活動.在數學教學過程中，通過活動，學生獲得良好的思維啟迪．好的問題是活動進行的紐帶，在教學中我們要選擇具有開發價值的問題，從數學知識的發生發展過程，特別是如何發現和提出數學問題、獲得數學對象的角度，結合具體內容發展學生的數學核心素養，使學生能自覺地用數學的思維方法去觀察、分析、解決問題，由“理性思維”逐步走向理性精神，把“立德樹人”真正地落實在平時的一題一 課中．