數(shù)學(xué)史融入問題支架式概念教學(xué)研究
——以“函數(shù)”第1課時教學(xué)為例*

李欣欣 (江蘇省蘇州市陽山實驗初級中學(xué)校 215151)

1 基本情況分析

1.1 學(xué)情分析

在學(xué)習(xí)本節(jié)課之前，學(xué)生已經(jīng)掌握用字母表示數(shù)、一元一次方程以及位置的變化等內(nèi)容，在這些內(nèi)容的基礎(chǔ)上，學(xué)生已經(jīng)能夠在變量之間建立關(guān)系．

1.2 課標解讀與教學(xué)目標

《義務(wù)教育數(shù)學(xué)課程標準(2022年版)》要求學(xué)生能夠探索簡單實例中的數(shù)量關(guān)系和變化規(guī)律，了解常量、變量的意義；了解函數(shù)的概念和表示法，能舉出函數(shù)的實例[1]．

教學(xué)目標 (1)借助情境問題支架，了解常量與變量的意義，能夠確定實際問題中的常量與變量；(2)掌握在一個變化過程中函數(shù)的概念，能判斷兩個變量之間是否存在函數(shù)關(guān)系，能分清函數(shù)關(guān)系中的自變量與因變量；(3)學(xué)會用函數(shù)的思想認識世界，用數(shù)學(xué)的語言描述世界的變化，在數(shù)學(xué)史的融入過程中增強民族自豪感．

教學(xué)重點 認識常量與變量，能夠判斷在一個變化過程中兩個變量之間是否存在函數(shù)關(guān)系．

教學(xué)難點 領(lǐng)悟在函數(shù)關(guān)系中因變量隨自變量變化而變化，確定而確定的關(guān)系；能夠聯(lián)系實際生活舉例并分析其中的函數(shù)關(guān)系，發(fā)展抽象能力．

2 主要教學(xué)過程

2.1 情境引入

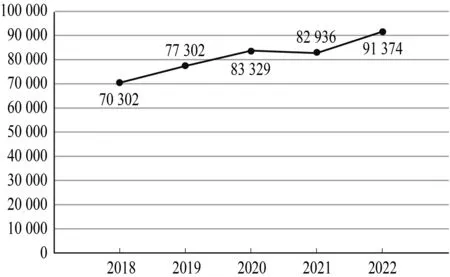
情境1 一列高鐵從蘇州出發(fā)，駛向南京，全程約220 km，假設(shè)列車始終以200 km/h的速度勻速行駛．在行駛過程中，記行駛時間為t，已行駛的路程為S1，未行駛的路程為S2(0

問題1在列車行駛的過程中，哪些量是沒有變化的？哪些量是不斷變化的？

生1：行駛時間是沒有變化的．

師：行駛過程中的時間是沒有變化的？

生1：速度是沒有變的，始終是200 km/h，變化的是已行駛的路程S1、未行駛的路程S2．

師：你說得很好，還有要補充的嗎？

生1：行駛時間是不斷變化的，但是行駛時間是有范圍的．

師：還有同學(xué)要補充嗎？

生2：行駛總路程220 km也是不變的．

師：觀察得很仔細，補充得也很完整．在一個變化過程中，我們將數(shù)值保持不變的量叫做常量，可以取不同數(shù)值的量叫做變量[2]．

問題2列車行駛過程中，S1與t，S1與S2之間存在怎樣的關(guān)系式？

生3：S1+S2=200，S2=200-S1．

師：你描述的是同一個問題的不同表現(xiàn)形式，還有其他的關(guān)系式嗎？

生4：S1=200t．

問題3在上述的關(guān)系式中，兩個變量又是如何變化的呢？

生5：S1如果增多了，那么S2就減少了．

師：也就是說如果S1變化，則S2也在變化．同樣地，如果S2變化，則S1也在變化．

生6：時間t在增大時，S1也在增大．

師：那么時間能不能一直增大？

生(眾)：不能，時間有范圍．

師：對，那么我們可以表述為時間t在一定范圍內(nèi)增大，S1也在增大．當時間t確定時，S1也確定．

情境2 愛動手操作的小明同學(xué)發(fā)現(xiàn)通過適當擺放火柴棒可以搭出小魚的形狀(圖1)．

圖1

問題1填寫表1．

表1

生7：搭一條小魚用了2+6=8根火柴棒，搭二條小魚用了2+6×2=14根火柴棒，搭三條小魚用了2+6×3=20根火柴棒，搭n條小魚用了(2+6n)根火柴棒．

師：你的回答全部正確，那么對于最后一個表達式，有沒有同學(xué)有不一樣的表達形式的？

生8：我認為也可以用8+6(n-1)來表示，可以解釋為搭一條小魚用了8根火柴棒，搭兩條小魚用了8+6×1根火柴棒，搭三條小魚用了8+6×2根火柴棒，那么搭n條小魚用了8+6(n-1)根火柴棒．

師：解釋得非常好，雖然我們化簡后的形式是一致的，但是思考的角度不同．

問題2這個情境中的常量與變量分別是什么？

生9：常量是6根火柴棒，每增加一條小魚，都增加6根火柴棒．

生10：變量是小魚條數(shù)和火柴棒根數(shù)．

問題3對于一個確定的n值，對應(yīng)的s有幾個？你能說說n與s這兩個變量是如何變化的嗎？

生11：對應(yīng)的s有一個．

師：更精準地說，是有……？

生(眾)：對應(yīng)的s有唯一的一個．

師：這也就反映了n與s這兩個變量是如何變化的呢？

生12：當n確定時，s也就確定；當n變化時，s也就變化．

情境3 圖2表示的是蘇州近幾年參加中考的學(xué)生人數(shù)．

圖2 參加中考人數(shù)

問題1圖2中的變量是什么？

生13：變量是年份和參加中考的人數(shù)．

師：此時的兩個變量之間還能寫出關(guān)系式嗎？

生(眾)：不能．

問題2根據(jù)圖2中的數(shù)據(jù)，你能說一說2020年和2021年參加中考的人數(shù)嗎？對于一個確定的中考年份，參加中考的人數(shù)有幾個與之對應(yīng)？

生(眾)：2020年有83 329人參加中考，2021年有82 936人參加中考．對于一個確定的中考年份，參加中考的人數(shù)有唯一的值與之對應(yīng)．

問題3年份與參加中考人數(shù)兩個變量是如何變化的？

生14：隨著年份的增大，參加中考的人數(shù)在增多．

師：是這樣的變化嗎？

生15：從2020年到2021年，年份在增大，但是參加中考的人數(shù)在減少．

師：那這兩個變量之間的關(guān)系應(yīng)該如何描述呢？

生15：應(yīng)該是參加中考人數(shù)隨著年份的變化而變化，同樣參加中考人數(shù)隨著年份的確定而確定．

師：我們再一起來感受一下這個詞“變化而變化、確定而確定”，剛才的同學(xué)描述得很準確．其實隨著年份的增大，參加中考的人數(shù)可能也會不斷減少或者增多減少交替，這是無法預(yù)測的，因此我們只能說是參加中考人數(shù)隨著年份的變化而變化．

情境4 石頭投入平靜的水面會形成圓形的水波向外擴散，圓的面積設(shè)為S，周長設(shè)為C，半徑設(shè)為r．

問題1問題中的變量有哪些？

生16：圓的面積S，圓的周長C，圓的半徑r．

師：在這個問題中，變量之間還存在著和前面一樣的關(guān)系嗎？

生(眾)：存在．

師：這里你能寫出兩個變量之間的關(guān)系式嗎？

生17：S=πr2，C=2πr．

問題2這個問題中也存在像上面一樣的關(guān)系嗎？

師：你能不能和前面一樣幫助我們分析一下兩個表達式中變量之間的關(guān)系？

生17：面積和周長隨半徑的變化而變化，確定而確定．

設(shè)計意圖前3個情境借助生活問題、數(shù)學(xué)問題，搭建問題支架，引導(dǎo)學(xué)生理解在一個變化過程中兩個變量之間的關(guān)系．通過解析式、列表、圖象等方法，多維度感悟函數(shù)的表達方式．最后一個情境，讓學(xué)生發(fā)散思維，主動探究變量之間存在的關(guān)系，提升學(xué)生學(xué)科素養(yǎng)．

2.2 歸納總結(jié)

師：從上面的4個情境中，同學(xué)們能否總結(jié)出它們的共同點？

生18：都含有變量，而且一個變量會隨著另一個變量變化而變化，確定而確定．

師：還有嗎？

生19：都是研究兩個變量之間的關(guān)系．

生18：一個變量與另一個變量是對應(yīng)的．

設(shè)計意圖讓學(xué)生提煉總結(jié)4個情境的共同點，為生成概念作鋪墊．

2.3 生成概念

師：滿足上述關(guān)系的兩個變量是如何定義的呢？首先前提條件是什么？

生(眾)：在一個變化的過程中兩個變量之間的關(guān)系．

師：很好，一般地，在一個變化過程中的兩個變量x和y，如果對于x的每一個值，y都有唯一的值與它對應(yīng)，那么稱y是x的函數(shù)[2]，其中x是自變量，y是因變量．

師：我們來看一下這個定義，哪些是關(guān)鍵詞？

生20：我認為是變化的過程，兩個變量，唯一對應(yīng)．

師：我們一起再來感受一下函數(shù)的定義．

設(shè)計意圖利用2.2總結(jié)的共同點，引導(dǎo)學(xué)生自然地生成函數(shù)概念．

2.4 情境再現(xiàn)

師：再回顧前面的4個情境，你能說說每個情境中自變量和因變量分別是什么嗎？哪一個變量是哪一個變量的函數(shù)呢？

生21：在情境1中S1是自變量，S2是因變量，S2是S1的函數(shù)．

師：有沒有和他想法不一樣的？

生22：S2是自變量，S1是因變量，S1可以是S2的函數(shù)．

師：這里能否說明S1或S2一定是自變量？

生(眾)：沒有，都可以．

生23：第二個式子中自變量是t，因變量是S1，S1是t的函數(shù)．

生23：情境2中n是自變量，s是因變量，s是n的函數(shù)．

生24：情境3中年份是自變量，參加中考的人數(shù)是因變量，參加中考的人數(shù)是年份的函數(shù)．

生24：r是自變量，C是因變量，C是r的函數(shù)；r是自變量，S是因變量，S是r的函數(shù)．

設(shè)計意圖再次回顧前面學(xué)習(xí)的情境，加深對函數(shù)概念的理解．

2.5 模型應(yīng)用

師：我們的生活中是否存在函數(shù)的模型呢？小組討論，一會兒請同學(xué)們說一說．

生25：超市每天的營業(yè)額隨著時間的變化而變化，營業(yè)額是自變量．

師：請你再思考，營業(yè)額是自變量嗎？

生25：時間是自變量，營業(yè)額是因變量，營業(yè)額是時間的函數(shù)．

生26：煮飯時，放多少米是自變量，放多少水是因變量，放的水量是米量的函數(shù)．

師：很不錯，這位同學(xué)善于觀察我們生活中的知識．

生27：一個修正帶用完的部分是自變量，沒有用的是因變量，沒有用的修正帶是已經(jīng)使用的修正帶的函數(shù)．

生28：一個人的身高是年齡的函數(shù)．

生29：平面鏡在反射光時，反射角是入射角的函數(shù)．

生30：買水果時，花費的金額是購買數(shù)量的函數(shù)．

生31：水在煮沸過程中，水的溫度隨時間的變化而變化，所以水的溫度是時間的函數(shù)．

生32：家中用來記錄時間的沙漏，漏下的沙子是自變量，沒有漏完的沙子是因變量，沒有漏完的沙子是已經(jīng)漏下沙子的函數(shù)．

師：其實我們的生活中到處都存在著函數(shù)關(guān)系，需要我們從數(shù)學(xué)的角度去思考生活中的問題，這樣一定會收獲頗豐．

設(shè)計意圖讓學(xué)生通過觀察思考，舉出生活中函數(shù)的例子，將函數(shù)概念運用于實際生活，在加深函數(shù)概念理解的同時，感悟數(shù)學(xué)與生活的緊密聯(lián)系．

2.6 追根溯源

師：同學(xué)們，你們知道“函數(shù)”一詞在古代中國最早是由誰提出的嗎？我們一起來了解一下函數(shù)的發(fā)展歷史吧．1859年，清代數(shù)學(xué)家李善蘭在翻譯《代數(shù)學(xué)》一書時，首次將function一詞翻譯為函數(shù)并引入我國．其中函通含，李善蘭將函數(shù)翻譯為“凡式中含天，為天之函數(shù)”．古代將天、地、人、物對應(yīng)于未知數(shù)，故可以解釋為凡是公式中含有變量x，則該式子叫做x的函數(shù)[3]．

師：在古代中國函數(shù)一詞雖是翻譯過來的，但其實早就有運用函數(shù)思想的例子了，比如我們熟知的二十四節(jié)氣表(圖3)．

圖3

師：在圖3中，我們可以發(fā)現(xiàn)每個節(jié)氣日期不是固定不變的，每一個節(jié)氣日期是隨年份變化而變化的，我們可以說每一個節(jié)氣日期是年份的函數(shù)；同樣節(jié)氣是隨太陽到達黃經(jīng)的度數(shù)變化而變化的，所以節(jié)氣是太陽到達黃經(jīng)度數(shù)的函數(shù)．

設(shè)計意圖將數(shù)學(xué)史融入數(shù)學(xué)課堂，讓學(xué)生了解古代中國函數(shù)發(fā)展的歷史，激發(fā)學(xué)生學(xué)習(xí)數(shù)學(xué)的好奇心．

2.7 總結(jié)課堂(略)

3 課堂反饋與教學(xué)感悟

3.1 問卷反饋

通過本節(jié)課的學(xué)習(xí)，45%的學(xué)生認為函數(shù)這節(jié)課難度簡單，55%的學(xué)生認為難度一般；88%的學(xué)生能夠清楚地說出什么是函數(shù)，45%的學(xué)生認為完全可以將函數(shù)關(guān)系解釋給其他人聽，48%的學(xué)生覺得基本可以將函數(shù)關(guān)系解釋給別人聽；70%的學(xué)生很期待接下來的函數(shù)學(xué)習(xí)，20%的學(xué)生期待接下來的學(xué)習(xí)但又忐忑擔心學(xué)不好．在如何學(xué)好函數(shù)的方式上，學(xué)生提出了可以多讀與函數(shù)有關(guān)的數(shù)學(xué)歷史著作、向老師請教、自己查閱資料等，也有一些學(xué)生認為通過多做練習(xí)可以更好地學(xué)好函數(shù)．從問卷的結(jié)果來看，大部分學(xué)生在本節(jié)課中掌握得較好，能夠?qū)⒑瘮?shù)的關(guān)系解釋清楚．從課堂情況來看，他們積極參與，能夠用生活中的實例解釋函數(shù)關(guān)系，充分地將生活實際與數(shù)學(xué)相結(jié)合．有了本節(jié)課的鋪墊，學(xué)生對學(xué)好一次函數(shù)、反比例函數(shù)、二次函數(shù)等其他函數(shù)也更有信心．在學(xué)習(xí)函數(shù)方式上，有部分學(xué)生提到了可以通過閱讀與函數(shù)有關(guān)的數(shù)學(xué)歷史著作，充分地說明了數(shù)學(xué)史融入課堂產(chǎn)生了積極有效的影響，對學(xué)生學(xué)好數(shù)學(xué)是大有裨益的．

3.2 教學(xué)感悟

(1)緊扣課標要求，搭建問題支架.根據(jù)課標的要求，本節(jié)課設(shè)置了4個主要情境，在每個情境基礎(chǔ)上搭建適切的問題支架，由易到難，助推學(xué)生的自主思考與探究．在第四個情境展示出來時，即使不出現(xiàn)前面具有引導(dǎo)性的問題，學(xué)生也能認識到第四個情境的意義是什么，這就是問題支架式教學(xué)的優(yōu)勢所在，助力學(xué)生主動思考，激發(fā)學(xué)生學(xué)習(xí)興趣．

(2)注重概念生成，強化概念理解.函數(shù)是一個很抽象的概念，因此本節(jié)課借助了大量情境讓學(xué)生理解并感知.在函數(shù)概念生成后，不急于做題，而是回頭看，充分利用好這些情境，帶領(lǐng)學(xué)生再學(xué)習(xí)之前情境中存在的函數(shù)關(guān)系，進而強化對函數(shù)概念的理解．函數(shù)概念來源于生活模型，在充分學(xué)習(xí)函數(shù)概念后，讓學(xué)生思考并舉出生活中存在的函數(shù)關(guān)系例子以繼續(xù)加深對函數(shù)概念的理解，感悟函數(shù)關(guān)系在生活中是無處不在的，綜合數(shù)學(xué)運算和數(shù)學(xué)抽象等素養(yǎng)，幫助學(xué)生在自己的腦海中建立相應(yīng)的數(shù)學(xué)概念[4]．

(3)融入數(shù)學(xué)歷史，加強德育滲透.在教學(xué)過程中，要讓學(xué)生知其然并知其所以然，因此函數(shù)概念的產(chǎn)生以及名稱的含義是需要教師解釋清楚的．在這里引入清代數(shù)學(xué)家李善蘭和函數(shù)之間的故事，推動本節(jié)課的教學(xué)更上一個層次，也讓學(xué)生近距離感受古代數(shù)學(xué)家的智慧．借助非物質(zhì)文化遺產(chǎn)代表作二十四節(jié)氣，向?qū)W生展示古人在編制二十四節(jié)氣時就已經(jīng)在運用函數(shù)的思想了．古人在生產(chǎn)農(nóng)耕時，仔細觀察天體運行，將日期、氣候、太陽到達黃經(jīng)度數(shù)等方面變化規(guī)律形成了科學(xué)的知識體系，由此可見數(shù)學(xué)與生活是緊密相關(guān)的．借此鼓勵學(xué)生用數(shù)學(xué)的眼光看待世界，用數(shù)學(xué)的思維分析世界，用數(shù)學(xué)的語言描述世界，增強學(xué)生學(xué)習(xí)數(shù)學(xué)的自信心，培養(yǎng)學(xué)生的民族自豪感，將德育滲透在日常的每一節(jié)課中．