做好課標對比研究 貫通核心素養培養

偶偉國 (江蘇省太倉市教育督導與質量監測中心 215400)

2022年4月，《義務教育課程方案(2022年版)》以及各學科課程標準正式頒布，引起了教育界廣泛關注，義務階段學校掀起了學習新課標的熱潮，高中段學校對此卻反響平平．但筆者以為，高中教師也有必要去研讀義務教育階段新課標，認真把握好義務教育階段新課標的新精神、新要求，做好與高中2017年版課標的對比研究，這樣才能有利于做好初高中教學銜接，有利于促進學科核心素養培養不斷走深、走實．那么，如何做好新課標的研究，做好學科素養的貫通培養？下面結合學習研究與教學實踐談談做法與體會．

1 從整體性視角做好課標研究

解讀2022年版的義務教育階段課標，可以用“一二三四五”來概括.一個核心：核心素養；兩條路徑：綜合育人、實踐育人；“三有”目標：培養有理想、有本領、有擔當的時代新人；四大突破：素養課程目標、課程內容結構化、學科實踐、學業質量標準；五項對策：教學評一體化教學原則、大單元設計、結構化思維教學、跨學科主題學習和項目化學習、作業與命題設計改革．由此可見，2022年版義務教育階段課標與2017年版的高中新課標體現了較好的一致性與傳承性．以數學學科為例，把全面貫徹黨的教育方針、落實立德樹人根本任務都作為修訂課標的指導思想．課程方案都進一步明確了各段學生培養目標，優化了課程結構，強化了課程有效實施的制度建設．

義務教育新課程標準與高中新課標相一致，旗幟鮮明地提出了以核心素養為導向，培養學生正確價值觀、必備品格和關鍵能力，編制了相應的學業質量標準．這些都標志著基礎教育將真正從知識掌握、能力提升為目標轉型為素養導向的新課程要求.如何積極應對新課程改革，我們必須要整體把握好兩個階段課標的核心要義，用好知識載體，積極探索全學段新課程背景下的新教育，落實立德樹人根本任務，在貫通培養學生學科核心素養上持續發力．

2 從連貫性視角做好教學銜接

貫通培養學科核心素養，做好教學銜接是關鍵.以往，銜接教學更多側重于知識和方法，而在全學段新課標的背景下，應著力做好核心素養銜接培養．以數學學科為例，義務教育階段課標指出，培養學生的數學核心素養，要“三會”，即是會用數學的眼光觀察現實世界、會用數學的思維思考現實世界、會用數學的語言表達現實世界．而高中段課標，也同樣倡導“三會”．因此，連貫性的銜接教學就應以知識銜接為依托，做好“三會”的傳承和創新，在探究新知的過程中發展能力，提升素養．

案例1函數的單調性．

對于函數單調性，初高中教材都是通過生活實例來引入，目的在于培養學生會用數學眼光，從現實世界的客觀現象中發現變量之間的關系,進而提出有意義的數學問題．對于單調性，初中教材依據變量說來研究變量之間存在的特殊關系，高中教材則著重研究函數所具有的這種特殊的內在性質，本質上兩者是一致的，但如何用更簡潔、更精準的數學語言來描述這一性質，是高中深化研究函數單調性的核心，是用數學語言表達現實世界的一個典例，既能完善學生認知結構，更為后續研究函數其他性質提供范式．

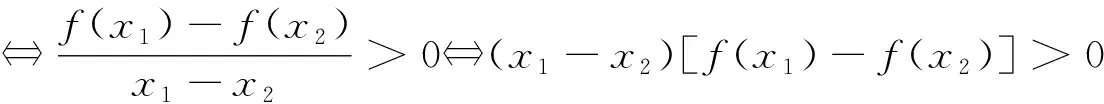
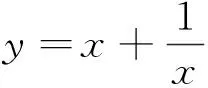
探究該問題，學生首先遇到的難點是，憑借已有知識很難勾畫出這個“對勾”函數的大致形狀.這就倒逼學生要借助單調性定義去開展研究．

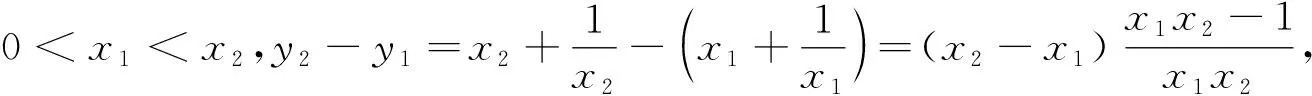
以上改編課本例題的做法，旨在充分挖掘例題潛在功效，讓學生在習得更多知識、方法的同時，又能拓展思維，提升素養．這樣處理教材的方式，也讓教師對銜接教學有了更深層次的理解與認識．

3 從發展性視角做好素養培養

課標指出，核心素養具有整體性、一致性和階段性的特征，在不同階段具有不同表現．小學階段側重對經驗的感悟，初中階段側重對概念的理解，高中階段側重對知識的探究．兩段課標均指出，教師要把教學活動的重心放在促進學生學會學習上，積極探索有利于促進學生學習的多樣化教學方式，不應僅限于講授與練習，也應包括引導學生閱讀自學、獨立思考、動手實踐、自主探索、合作交流等．在高中教學中，不妨從初中練習中選擇一些典型問題，讓學生在學習了相關高中知識后，嘗試用新知識來探究老問題，讓學生體會到對于同一個問題，知識越多則觀察問題的視角越多，增加了解決問題的路徑．在充分感受知識學習的必要性、破解問題的同時，學生學科核心素養也潛移默化地得到了提升與發展．

案例2一個中考模擬題的多角度探究．

(2022太倉、昆山中考模擬試題)如圖1，等邊三角形ABC邊長為2，D是BC中點，E在AD上運動，連結BE，在BE下方作等邊三角形BEF，則△BDF周長的最小值為( )．

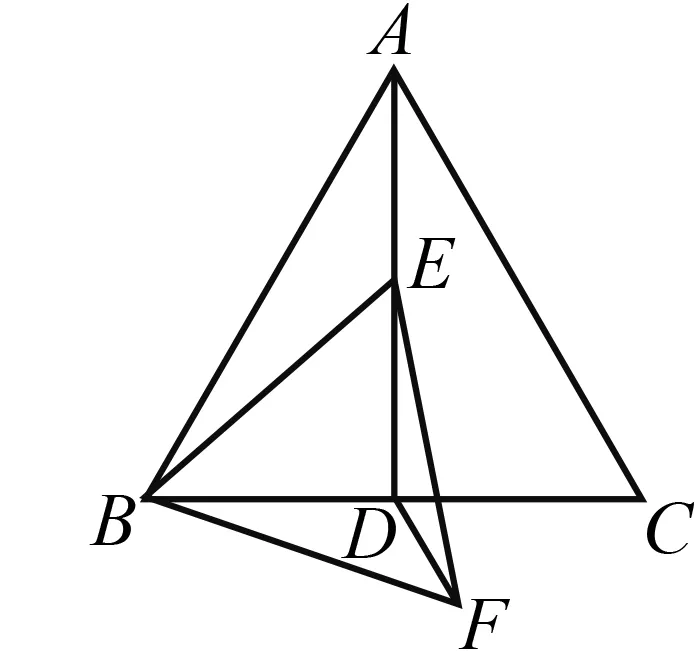
圖1

分析 研究△BDF的周長，關鍵要研究點F的變化情況，點F是隨著點E的變化而變化．由于點E在定線段AD上運動，猜測點F也應有較規則的運動軌跡．

方法1 (幾何法探尋點F的運動軌跡)連結CF，證△ABE≌△CBF，由此得∠BCF=BAD=30°，即點F在過點C且傾斜角為30°的直線上運動．這樣將問題轉化為直線上找一點，使得它與兩定點的距離之和最小．

說明兩個三角形全等，蘊含了變化中的不變性，給代數推理尋找到了有效突破口．

方法2 (代數法探尋點F的運動軌跡)點F的變化是由點E的運動變化引發的．借助函數觀點，點E的變化導致了∠EBC的變化．由此，可以以點B為原點、BC為x軸建立平面直角坐標系(圖2)．

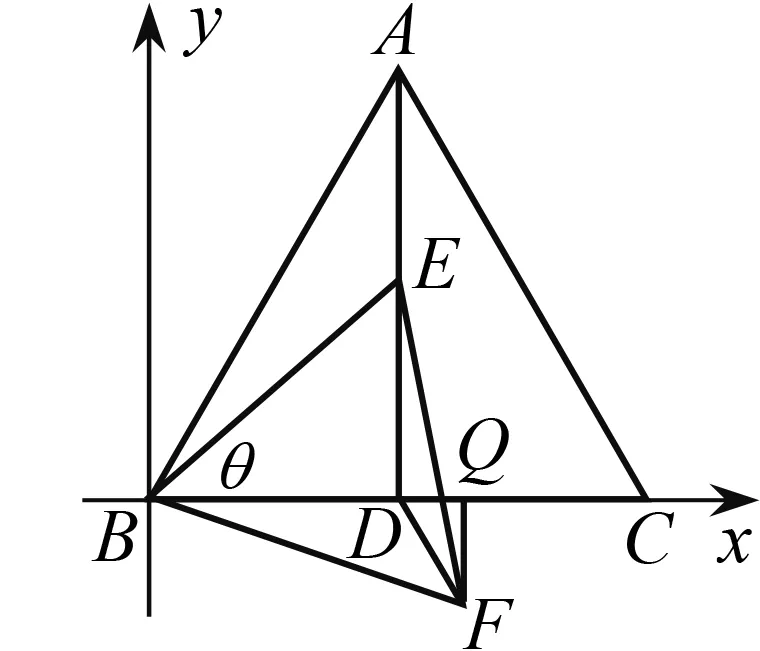
圖2

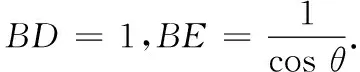
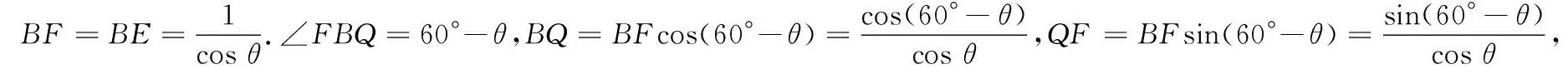
說明此方法是學生在學習了三角函數知識后，應用所學知識再來研究初中研究過的運動變化問題．用函數觀點來研究，既為問題解決提供了不同的方法，也為提升學生代數推理能力和素養創造了時機．

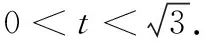
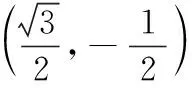
說明換元后轉化為函數最值問題，既可從探尋數式蘊含的幾何意義出發來嘗試解決問題，又可以在學習導數知識后來解決．

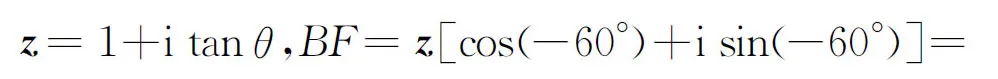
說明復數乘積的幾何意義為研究運動變化問題提供了新路徑．

隨著高中學習的展開，一個初中練習中常見的運動變化最值問題的解決路徑越來越多，在不斷開拓學生視野的同時，也不斷發展著學生的學科核心素養．這個案例，為教師如何找準發展學生學科素養的切入點提供了研究樣式．

新課標呼喚新使命，每位教師都應扛起立德樹人的責任擔當，立足當下，在素養導向下，教好書、育好人，培養好學生學科素養．同時，更要做好教育傳承工作，持續發展好學生核心素養，為他們未來的學習與生活奠基．