一種新型基于共用系數的二維ANCF 高階梁單元

周川，趙春花，獨亞平，郭嘉輝

（201620 上海市 上海工程技術大學 機械與汽車工程學院）

0 引言

絕對節點坐標法（簡記為ANCF）[1]是由美國伊利諾伊大學的夏巴那教授提出的一種解決多體系統大變形大轉動的新型有限元方法。不同于牛頓歐拉法[2]、凱恩法[3]等其它的多體系統建模方法[4-6]，ANCF 法拋棄了傳統有限元小變形假設，將轉角以梯度形式表示引入到節點自由度中，得到的質量矩陣為常數陣且不存在科氏力、離心力，提出至今受到越來越多學者們的關注和研究。

研究前期，Omar 等[7]提出的二維ANCF 全參數剪切梁單元通過一般連續介質力學方法構建單元彈性力，但一般連續介質力學方法構建的單元存在一些閉鎖問題[8]；沈振興[9]和張大羽等[8]學者認為，全參數梁的位移模式在橫向橫縱向的插值不一致，導致無法滿足廣義胡克定律，產生了偽應力，使得單元計算性能下降。為解決該問題，Zhao 等[10]通過共用系數法在橫向插值中引入y2，使得全參數剪切梁橫縱向插值保證了2 階次，取得了不錯效果；Patel 等[11]基于獨立系數引入曲率坐標，構建新的橫向高階單元，橫縱向插值達到2 階一致，有效減輕了閉鎖問題，同時還提出了應變分裂法解決ANCF 梁和板單元中存在的閉鎖問題；Li 等[12]在二維全參數梁基礎上增加曲率自由度rxy，同時通過共用插值項系數引入了橫向高階x2y2，但是計算結果并沒有很好地改善；於祖慶[13]提出了幾種絕對節點坐標單元，并將新單元用于車輛鋼板彈簧和輪胎的動力學建模中；徐齊平[14]提出了超彈性ANCF 單元，并將其用于建立氣動軟體機器人的精確動力學模型。

本文在Li 提出的單元自由度[12]基礎上，通過共用系數引入橫向高階插值項，提出了一種新的梁單元。通過理論推導結合數值實例，證明了新單元的可行性，能夠緩解泊松閉鎖問題，提高單元收斂精度。

1 二維ANCF 橫向高階剪切梁單元

Li 等引入曲率坐標的同時，共用插值項系數，引入了橫向高階插值項-3x2y2，建立了一種新的二維ANCF 橫向高階剪切梁單元[12]，文中簡記為單元LPF。本文在此基礎上再一次通過共用x3系數，改為引入不同橫向高階插值項y2，構建了新的二維高階梁單元，記為E1，其位置矢量為：

根據文獻[10]，低階單元橫縱向插值不一致使得其并不滿足廣義胡克定律。

根據應力應變關系σ=Dε，有

不考慮橫縱向高階耦合項時有

聯立式（2）和式（3），有

根據橫縱向應變的定義，有

因此，新單元中通過共用系數引入的橫向高階插值項y2并能夠滿足廣義胡克定律，可以較好地緩解泊松閉鎖問題，提高收斂精度。

2 動力學方程

絕對節點坐標法描述的二維梁單元動力學方程形式如下：

式中：Me——單元質量矩陣；Ke（e）——單元剛度矩陣；Qe——單元廣義外力列陣。

2.1 單元質量矩陣

式中：S——形函數矩陣；e——節點廣義坐標向量。質量矩陣由單元動能推導得到

因此，單元質量矩陣為

2.2 單元剛度矩陣

一般連續介質力學方法是ANCF 方法的基本力學原理。由格林-拉格朗日應變張量可得：

其中任意一點變形梯度為

由2 階張量的voigt 標記，將應變張量改寫為應變向量形式：

這里，泊松比v 會使得橫縱向正應變ε11和ε22發生耦合。

彈性力列陣：

式中：K（e）——剛度矩陣。

2.3 廣義外力列陣

單元在受到外力F 作用下，單元廣義外力為

3 數值實例

本節通過懸臂梁靜力學、動力學等數值實例，對新單元的力學性能進行測試。

3.1 靜力學大變形

懸臂梁如圖1 所示，尺寸為：長l=2 m，寬w=0.1 m，高h=0.1 m。楊氏模量E=2.07×1011Pa，泊松比v=0.3，在懸臂端點重力方向施加的集中力F=500 000 N。以有限元軟件ANSYS 中Beam 188單元仿真結果為參照。

圖1 大變形懸臂梁Fig.1 Large deformation cantilever beam

表1 是不同單元在不同單元數劃分下，懸臂梁端點處y 方向位移情況，圖2 是不同單元與ANSYS 計算結果的誤差情況。由表1 和圖2 可知，新單元E1 與原單元LPF 相比，收斂精度有明顯提高，泊松閉鎖問題得到有效緩解。單元數增加時，新單元與ANSYS 計算結果誤差接近于0。

表1 大變形下末端點Y 方向位移計算結果Tab.1 Calculation results of the displacement in Y direction of end point under large deformation

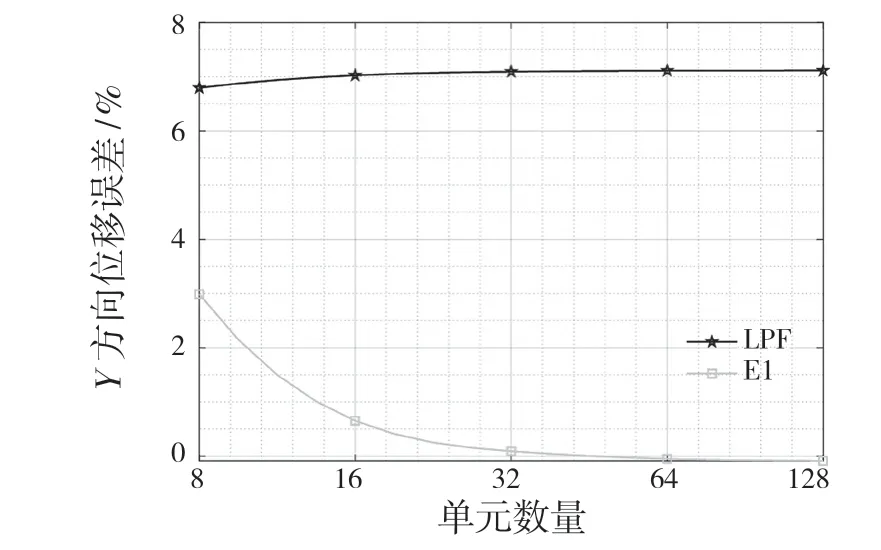
圖2 各單元與ANSYS 在Y 方向位移誤差Fig.2 Displacement error of each element in Y direction compared with ANSYS

3.3 單擺

單擺如圖3 所示，長l=1 m，寬w=0.006 32 m，高h=0.252 98 m，密度ρ=5 540 kg/m3，泊松比v=0.3，楊氏模量E=700 000 Pa，重力g 為外部載荷。計算0～1.1 s 單擺的運動情況，在MATLAB 平臺進行仿真計算。

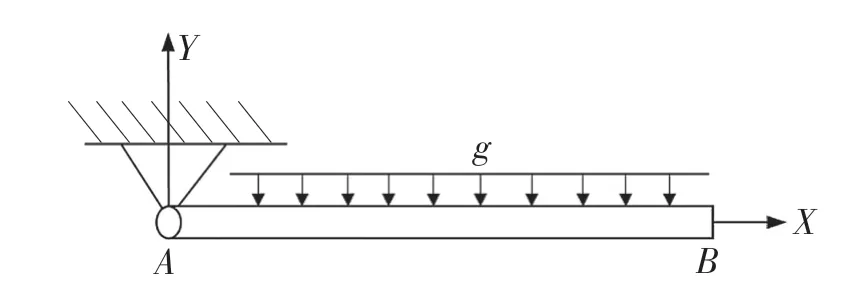
圖3 單擺模型Fig.3 Simple pendulum model

圖4 是不同時刻各單元位姿，圖5、圖6 是各單元末端點不同時刻下的x、y 方向位移情況。根據圖4 可知，不同時刻下，新單元的位姿與ABAQUS 軟件仿真結果基本一致。由圖5、圖6 可知，新單元E1 末端點不同時刻下X、Y 方向的位移情況與ABAQUS 末端點的位移也基本吻合。而單元LPF 與ABAQUS有限元軟件的結果存在較大誤差，故新單元能夠更精確地描述動力學大變形運動過程。

圖4 不同時刻各單元位姿Fig.4 Poses of each element at different moments,

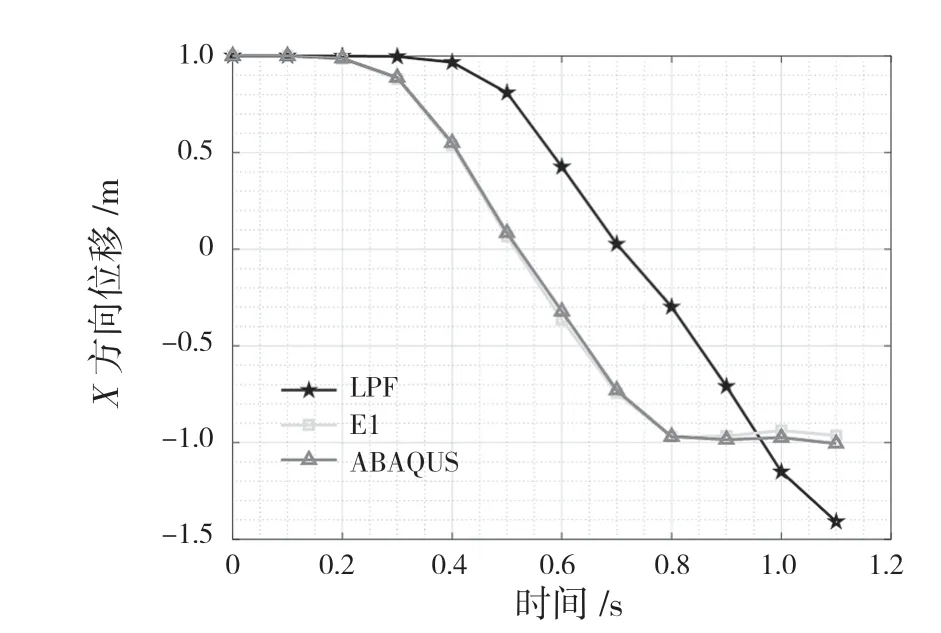
圖5 不同時刻各單元末端點X 方向位移Fig.5 Displacement of end points of each element in X direction at different time

圖6 不同時刻各單元末端點Y 方向位移Fig.6 Displacement of end points of each element in Y direction at different time

4 結論

本文提出了一種共用系數的二維ANCF 高階剪切梁單元，通過理論推導結合靜力學、動力學數值實例，證明了（1）新單元相較于單元LPF 能夠有效緩解泊松閉鎖問題，提高單元靜力學大變形中的的收斂精度。（2）相較于單元LPF，新單元能夠更加精確地進行動力學仿真和分析。