串聯式撈渣機器人運動學分析及ADAMS 仿真

李源，羅璟，袁安華，余長順

（650500 云南省 昆明市 昆明理工大學 機電工程學院）

0 引言

在金屬產品的冶煉生產過程中會生成一種影響產品質量的副產物——浮渣，它的產生是不能避免的。為了減少浮渣的生成量，除了需要嚴格控制金屬液的處理時間、金屬液的溫度、鍋爐的停車次數和時間等生產過程中的參數以外，最主要的就是使用外部設備（如除渣機器人等）來對金屬液進行定期的除渣工作，這樣可以使金屬液中的浮渣含量保持在一個相對穩定的范圍內。

目前，國內主要是通過工人手持簡易自制撈渣斗，撈取鋅冶煉鍋中的氧化渣。人工撈渣存在諸多問題，如撈渣不迅速不完全、效率不高、工作強度大、危害風險比較高等。工人如若不能及時徹底將氧化渣撈除，就會對鍍鋅板表面質量產生影響；撈渣效率低則會對鍍鋅生產線的自動化水平以及生產效率產生影響。人工撈渣要求工作人員在高溫有毒環境中工作比較長的時間，大大增加了工人的工作強度以及受危害的風險程度[1]。另外，人工撈渣會使鋅液泛起波紋，導致涂層厚度不一致，嚴重影響鍍鋅產品質量。鋅鍋動蕩增多則會增加鋅液與空氣的接觸，生成更多氧化物，使表面產生更多缺陷[2]。

為了提高撈取鋅渣的效率，降低工人的工作強度，在參考國內外撈渣機器人設計的基礎上，本文根據鄒慧君[3]和鐘毅芳[4],吳昌林等文獻的基本原理，設計了一種串聯式撈渣機械臂，可以在惡劣工況下工作。文中運用SolidWorks 軟件對撈渣機械臂的三維模型進行簡化，對打撈機器人正逆運動學進行分析，通過ADAMS 軟件對機械臂進行運動學仿真，得出末端法蘭的速度、加速度，進而說明本設計的合理性。

1 移動式撈渣機器人建模及運動學分析

1.1 機器人D-H 坐標系的建立及相關參數

移動撈渣機器人（如圖1）系統由2 部分組成，第1 部分是6 軸串聯機器人，第2 部分是線性導軌式滑臺。對導軌移動式撈渣機器人采用改進的D-H方法建立的坐標系如圖2 所示。圖2 中，7 號表示移動平臺的移動關節，1 到6 號分別表示機器人本體結構中6 個轉動關節，坐標系{0}是基礎坐標，實際上它和坐標系{7}是相互重合的，在建立的D-H坐標系中，起始末端點坐標為[825.5，0，1 080]。建立移動撈渣機器人的基坐標系{0}，設定基座參數分別為α0=0，a0=0，θ0=0°，d0=0°，通過坐標變換可得機器人連桿參數，具體參數如表1 所示。

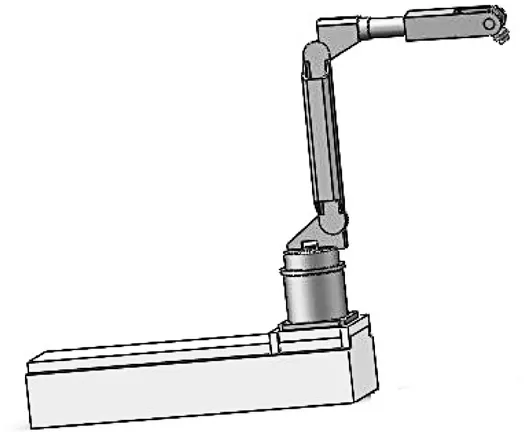
圖1 移動撈渣機器人示意圖Fig.1 Schematic diagram of mobile slag removing robot

圖2 移動撈渣機器人的D-H 坐標系Fig.2 D-H coordinate system of mobile slag removing robot

表1 撈渣機器人的D-H 參數表Tab.1 D-H parameters of slag robot

1.2 撈渣機器人的正運動學分析

通過建立撈渣機器人的D-H 連桿坐標系[5]，可以對機器人的每一個關節進行坐標旋轉變換和平移變換，這樣就可以得到撈渣機器人的末端位姿在世界坐標系里面的位姿矩陣。下述過程是將相互鄰接的兩連桿之間的矩陣進行齊次變換。Aij 為變換矩陣，它表示的是將坐標系{i}變到{j}，對每一個關節坐標系都可以進行相應的矩陣轉換，這樣就可以得到式（1）—式（9）的轉換矩陣：

移動式撈渣機器人的正運動學表達式如式（9）所示。式中，ci表示的是cosθ，si表示的是sinθ；式（9）中，Ni，Oi，Pi（i=1，2，…）則是關于連桿變量D、θi（i=1，2，3，4，5，6）的函數。

1.3 基于Robotics Toolbox 的正運動學分析仿真驗證

為了驗證上述的撈渣機器人運動學分析是否正確，使用 MATLAB 中的Robotics Toolbox 工具箱對其進行求解。工具箱中的 fkine 函數可以對機器人的末端位姿求解，如果機器人的末端位姿q=[0-pi/2 0 0 0 0]，則對應的變換矩陣為T=fkine（r，q）。圖3 所示為求解的程序以及結果。

圖3 MATLAB 求解末端矩陣Fig.3 MATLAB solution of terminal matrix

將θ1=0，θ2=-pi/2，θ3=0，θ4=0，θ5=0，θ6=0 代入式（9），求解機器人末端變換矩陣如式（10）所示。

比較發現，由矩陣變換求解出來的結果與fkine 函數求解出來的結果是一致的，結果證明機器人的 D-H 建模以及正運動學分析是正確的。

2 仿真模型的建立

采用ADAMS 2016 對移動式撈渣機器人進行運動學仿真分析 。具體運動學仿真分析步驟如下：

（1）對模型進行簡化并導入ADAMS

參考國內撈渣機器人設計的經驗[7]，由于本文在設計移動式撈渣機器人結構部件時沒有考慮齒輪軸承等部件，只是簡化后的機器人，因此可以直接導入 ADAMS 。需要注意的是，通過SolidWorks進行仿真模型轉換時2 個軟件之間的單位以及坐標系應該是統一的，這樣才能確保數據之間轉換正確。打開ADAMS 軟件，創建一個新的模型，將SolidWorks 軟件導出的parasolid.x_t 格式的文件導入，如圖4 所示。移動式撈渣機器人導入后的結構模型如圖5 所示。

圖4 撈渣機器人導入到 ADAMSFig.4 Slag removing robot imported into ADAMS

圖5 移動式撈渣機器人的結構模型圖Fig.5 Structure model diagram of mobile slag removing robot

（2）對機器人創建約束并添加驅動

在移動式撈渣機器人模型中，有固定不動的剛體，也有通過轉動副或移動副相互連接的剛體。機器人底座和移動平臺的滑塊是固定的，軌道和大地之間固定在一起，它們之間添加為固定副；軌道與滑塊之間可以移動，添加的是移動副；其余各關節之間均添加轉動副。通過ADAMS 中的STEP 函數完成對機器人驅動的添加，完成約束以及驅動的添加之后，撈渣機器人的模型如圖6 所示。

圖6 移動式撈渣機器人的模型結構Fig.6 Model structure of mobile slag removing robot

（3）對仿真模型進行驗證

運行仿真前，要求對前面處理好的仿真模型進行檢驗，特別是存在較多約束和驅動的仿真模型，這樣可以查看約束和驅動的具體添加情況，避免出現由于過約束或者欠約束致使仿真過程失敗。在工具中單擊驗證模型選項，本文模型驗證是成功的。

（4）進行仿真求解

完成上述的操作過程之后，運用STEP 函數進行仿真，仿真時間設置為7 s，仿真步數設置為300，運行仿真。

（5）仿真結果的后處理

仿真計算完成之后，可以在結果選項中查看結果以及進行后處理操作，輸出需要的曲線圖。

3 仿真結果分析

圖7 是撈渣機器人末端法蘭位移的變化曲線圖，從圖中可以分析看出，撈渣機器人的位移變化曲線比較平滑，表示機器人在給定的軌跡中運行平穩，沒有發生突變，說明機器人是可以達到實際工作要求的。

圖7 撈渣機器人末端法蘭位移的變化曲線Fig.7 Variation curve of end flange displacement of slag removing robot

圖8 是撈渣機器人末端法蘭的速度變化曲線，圖9 是撈渣機器人末端法蘭加速度變化曲線，圖10 是撈渣機器人末端法蘭的角速度變化曲線，圖11 是撈渣機器人末端法蘭的角加速度變化曲線。從速度和角速度變化曲線圖中分析得出，在機器人的仿真運行過程中，機器人的末端法蘭運行平穩，沒有出現突變的情況，滿足實際的工作需求。

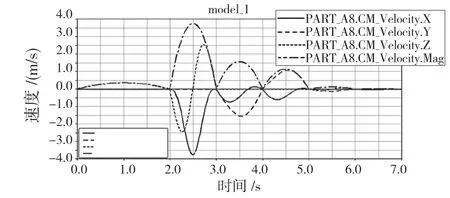
圖8 撈渣機器人末端法蘭的速度變化曲線Fig.8 Speed change curve of end flange of slag removing robot

圖9 撈渣機器人末端法蘭的加速度變化曲線Fig.9 Acceleration variation curve of end flange of slag removing robot

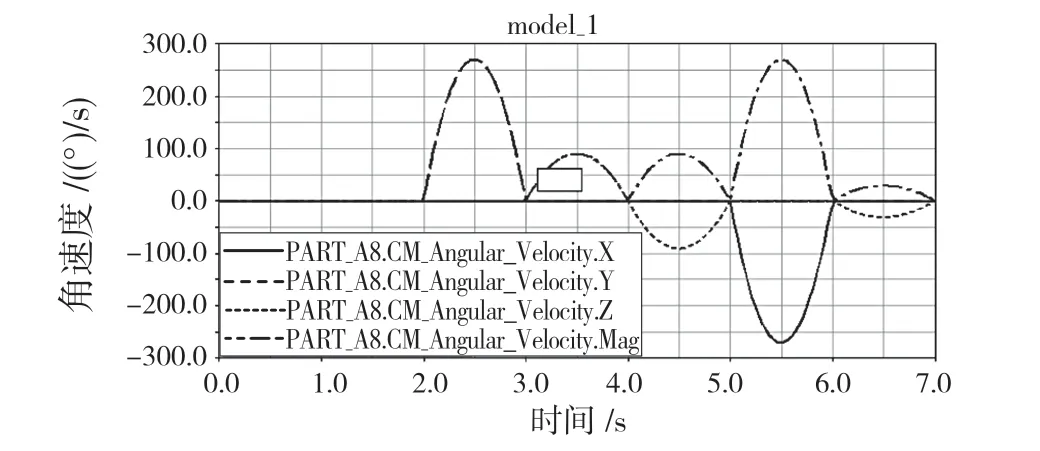
圖10 撈渣機器人末端法蘭的角速度變化曲線Fig.10 Angular speed change curve of end flange of slag removal robot

圖11 撈渣機器人末端法蘭的角加速度變化曲線Fig.11 Angular acceleration curve of end flange of slag removing robot

從加速度和角加速度曲線圖中分析得出，機器人在正常運動時加速度變化都比較平穩，但在末端法蘭剛啟動以及停止過程中出現角加速度突變，由0 變到一個較大數值，這是由不穩定受力造成的，重力、負載等會對加速度產生影響。在中間運行階段，受力穩定后，加速度變化也趨向穩定。為了避免機器人末端執行器在運行中的不平穩，可以考慮同時對每一個關節進行驅動，這樣能夠減緩因為多個關節相繼驅動而引起的加速度突變，同時還可以提高機器人的動作速度。

4 結語

為了提高撈取鋅渣的效率，降低工人的工作強度，設計了一種串聯式的撈渣機器人，對其進行了運動學分析。將三維模型導入ADAMS 軟件，通過施加約束和添加驅動，得出撈渣機器人末端法蘭的位移、速度、加速度等變化曲線圖，綜合分析可以得出，在本文所規劃的軌跡中，機器人末端執行器的位移、速度、加速度隨時間都是連續平穩變化的，運行過程中沒有發生較大的沖擊，運行相對平穩，可以滿足實際工作中的任務要求。