試論數學思想在高中化學解題中的應用

項 華

(福建省石獅市華僑中學 362700)

1 方程思想

方程思想是一種重要的數學思想，即按照一定的邏輯關系構建方程，將已知與未知參數建立聯系的一種思想，構建正確的方程是解題的關鍵.對于高中化學學科而言，構建方程的依據為各種守恒思想，如得失電子守恒、電荷守恒、原子守恒等，因此教學實踐中，教師應為學生做好這些守恒思想的深入解讀，使其把握守恒思想的精髓.

例1使用11.92 g NaClO配制溶液100 mL，向其中加入0.01 mol Na2Sx恰好完全反應生成Na2SO4和NaCl，則化學式Na2Sx中x的值為____.

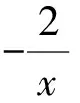
2 數形結合思想

數形結合思想是高中數學解題中常用思想之一.通過讀圖明確圖像縱橫坐標表示的含義，結合化學反應掌握圖線的變化規律，尤其注意圖線的拐點、交點等，不放過圖線中的細節.

例2將1mol HNO3和1mol H2SO4混合在一起后，逐漸向其中加入鐵粉至過量.溶液中金屬陽離子a、b和加入鐵粉的物質的量關系如圖1所示，其中稀硝酸的還原產物只有NO，則以下說法錯誤的是( ).

A.a為Fe3+的關系曲線

B.p點時Fe2+的物質的量為0.6 mol

本文重點講述的電力負荷的預測方法，就是將城市空間負荷分成多個單元區塊，并對各個單元區塊中負荷的類型和性質進行定義，然后，在這個基礎之上進行電力負荷的預測。這種預測方法可以實現對城市中任意的區塊在任意的預測年份進行電力負荷的預測，在配電網規劃中適應性較強。與傳統的電力負荷預測方法相比，空間負荷預測方法得到的結果更加精確，但同時還應看到的是，它對于各個單元區塊中的信息需求程度也更大。

C.n1的值為0.75

D.在p點加入銅粉，最多可溶解14.4 g

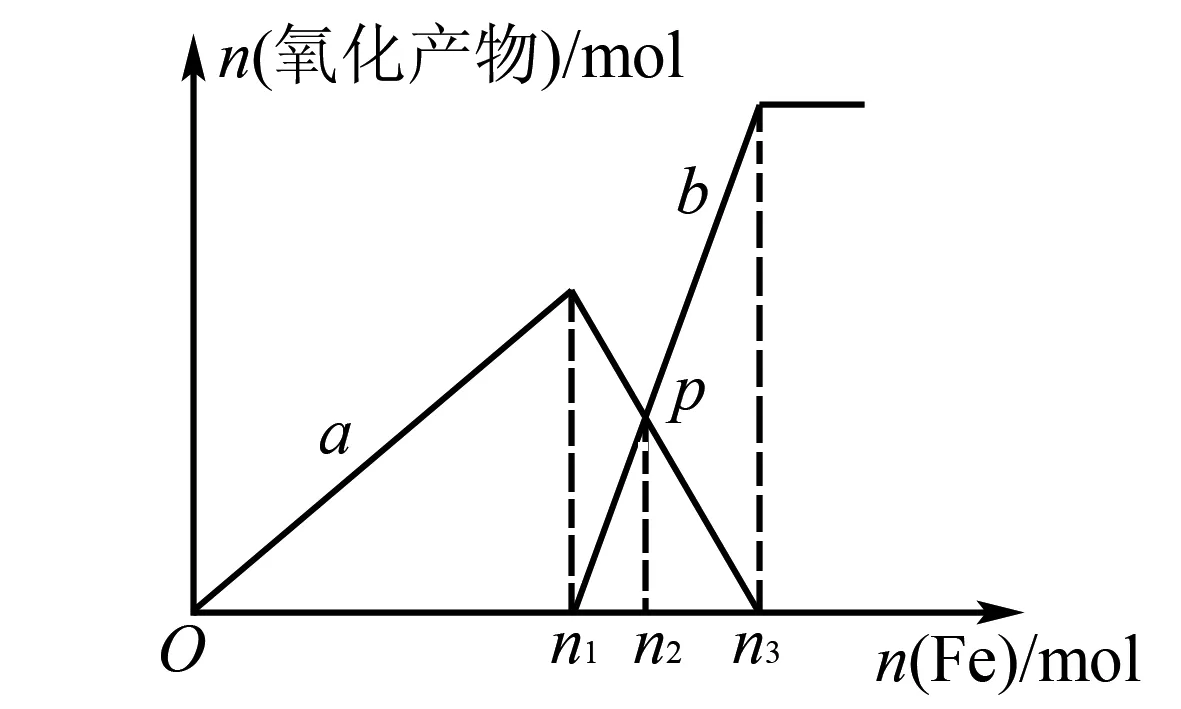
圖1

3 分類討論思想

分類討論思想是高中數學各類測試中常考的思想.事實上在分析高中化學問題時，如果對情境、參數、物質狀態不能做出準確的判斷，也需要進行分類討論.運用分類討論思想解答高中化學習題與解答數學習題的步驟基本一致，即根據題意確定分類討論的依據，按照一定順序或邏輯關系進行分析.

A.若X、Y均為氣體，平衡時氣體平均摩爾質量：Ⅱ>Ⅰ

B.若X、Y不均為氣體，則平衡時氣體平均摩爾質量：Ⅰ>Ⅱ

C.若X為固態，Y為氣態，則Ⅰ、Ⅱ從起始到平衡所需時間相同

D.平衡時Ⅰ的體積不足VL

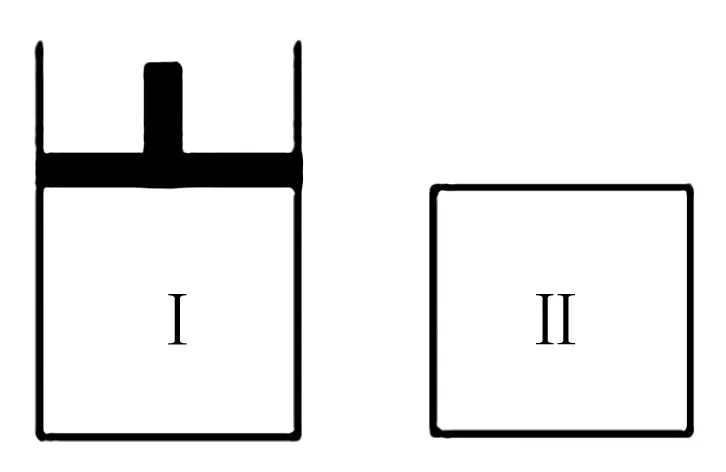
圖2

該題考查學生對平衡移動知識的理解以及靈活運用情況.因X、Y的狀態未知，因此，需要運用分類討論思想進行分析.根據題干設Y參加反應的物質的量為n列出三行式，結合X、Y、Z的物質的量之比為1∶3∶2可求出a的值為1.當X、Y均為氣體時Ⅰ和Ⅱ相比，Ⅰ相當于加壓平衡正向移動，氣體物質的量變小，對應的平均摩爾質量增大，即Ⅰ>Ⅱ.若X、Y不均為氣體且Y為氣體時，壓強對化學平衡無影響，兩容器的氣體平均摩爾質量相等.此時兩容器處于等效平衡狀態，從起始到平衡經歷相同時間且平衡時Ⅰ的體積仍為VL.綜上分析一定正確的是C項.

4 建模思想

建模思想是基于對問題本質的抽象理解，運用數學語言予以概括、表征的一種思想.高中化學涉及很多模型，如氧化還原反應模型、化學平衡模型、電化學模型等.這些模型是高中化學的重點，是各類測試的熱門考點.

A.放電時，M電極的電勢高于N電極

B.放電時，Li+通過陽離子交換膜到達M電極附近

D.充電時，1 mol Li2S4轉化為Li2S6電路中通過2mol電子

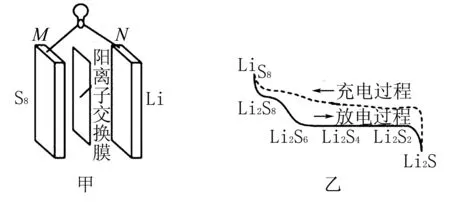
圖3

5 極限思想

極限思維是用極限概念分析問題和解決問題的一種數學思想.極限思想在高中化學學習中有著廣泛的應用，尤其在分析混合物的組成、化學平衡、物質參數取值范圍問題中時常運用到極限思想.

例5向100 mL 0.1mol/L的Fe2(SO4)3溶液中通入標準狀況下為aL的SO2與Cl2的混合氣體，充分反應后溶液棕黃色變淺.而后向反應后的溶液中加入足量BaCl2溶液，過濾、洗滌、干燥后稱量得到的沉淀，質量為11.65 g，則a的取值范圍為____.