高考圓錐曲線解答題的研究方向

謝賢祖

(廣東省華南師大附中汕尾學校 516699)

2020年全國各地的高考圓錐曲線解答題考法多樣，精彩紛呈，讓人津津樂道.很多題目既有高等背景，又有常規易懂的通性通法.不同試題以數學思想方法為引領，又兼顧考查幾大核心素養.有些題目源自往年經典考題，推陳出新，很好地考查了學生在新的情境下解決問題的能力.

1 研究教材，適度延伸

很多高考題都是源于教材而又高于教材，所以“回歸教材”必須成為我們備考復習的必經階段，但是不應該成為一句空話，而是要實實在在地研究教材習題的解題思想并且適當地對題目進行變式延伸，幫助學生總結能夠指導未來解題的“有效經驗”.下面舉例說明.

圖1

總結(1)以上三道題目都可以化歸為“求點到直線的距離最值”問題，這是我們老師應該向學生總結梳理的.

(2)求橢圓上的點到直線的距離最值，可以設平行切線再求兩線距離，也可以設橢圓參數方程用輔助角公式解決，這是對學生未來解題有幫助的“有效經驗”，需要我們老師引導學生總結積累.

(3)三道題目都考查了數形結合的思想和直觀想象的核心素養，啟發我們要引導學生，主動借助圖形性質去探索數學規律，解決數學問題.

(4)從歷年的高考題中可以看到很多競賽題的影子，競賽題經過演變很可能成為以后的高考題，所以研究競賽，找到高考與競賽的結合點對我們的備考大有裨益.下面提供一個與前面三個例題有關的升級版供讀者選用.

2 研究算理，積累結論

數學運算素養是解析幾何的核心素養，可以說“計算決定成敗”，所以經常思考如何簡化圓錐曲線中的復雜計算，可以幫助學生節省時間，準確作答，高效得分.根據《2017年版課程標準》對運算素養的描述，我們可以從運算對象、運算方法、運算程序等方面進行研究.

(k2a2+b2)x2+2a2kmx+a2m2-a2b2=0，

△=4a2b2(k2a2+b2-m2).

由此可知，△的正負取決于k2a2+b2-m2的符號.明白這一原理之后，可以為我們的解題帶來極大的便利.比如前面的四道例題，都要用到直線和橢圓相切，于是利用k2a2+b2-m2=0，這樣便可以快速解方程或者找到未知數之間的聯系.

再比如用“點差法”在處理“中點弦”問題時，比普通的聯立、消y、用韋達的套路要簡便得多，值得研究、積累、記憶結論.

證明設A(x1,y1)，B(x2,y2)，則

總結通過研究點差法的運算原理可知，拋物線的弦所在直線的斜率只取決于p和弦中點的橫坐標或者縱坐標.總結這一解題經驗，可以為我們“預判”解題方向，簡化計算，少走彎路.下面舉例說明.

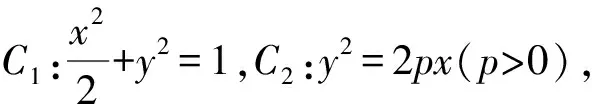
總結筆者看到此題的第一反應就是用結論1、結論2建立參數之間的聯系，再逐步消元，留下目標p，再求解p的范圍，于是輕松解決.但要跟學生強調，點差法的證明過程要在答卷上展示出來，避免直接使用結論而被扣分.

3 研究高等背景，高屋建瓴

很多圓錐曲線題目有深厚的高等背景，如果能知道它們的來龍去脈，在教學的時候便可居高臨下.如2020年全國Ⅰ卷理科20題與高等幾何中的極點極線有關，下面先補充相關知識背景.

極點極線的幾何定義如圖2，過橢圓外一點P作橢圓的兩條割線，分別交橢圓于A,B,C,D，連接AC，BD交于點E，連接DA，CB交于點F，則稱直線EF為點P對應的極線.同理可知直線EP為點F對應的極線，直線PF為點E對應的極線.所以我們把△PEF叫做“自極三角形”.

圖2 圖3

4 運用平面幾何知識解題

全國卷歷年的解析幾何題目，經常可以使用平面幾何知識處理，主要考查數形結合的思想和幾何直觀的核心素養，若從幾何圖形入手研究，發現圖形與數量之間的規律，則可以實現“多一點想，少一點算”.

圖4

總結由已知條件容易想到初中常見的全等模型，用割補法求三角形面積省去繁雜的計算，由此可見，運用平面幾何知識可以減輕計算負擔，歷年高考題，尤其是客觀題，經常可以數形結合，找到圖形規律再“秒殺”，值得我們深入研究.

5 研究通性通法，以不變應萬變

筆者把通性通法的研究放到本文最后才寫，就是為了突出它的重要性，面對變化多端的圓錐曲線解答題，唯有通法是王道.下面筆者以前面的例6,即2020年全國Ⅰ卷理科第20題為例，回歸基礎，將解決此題的通性通法詳細總結如下.

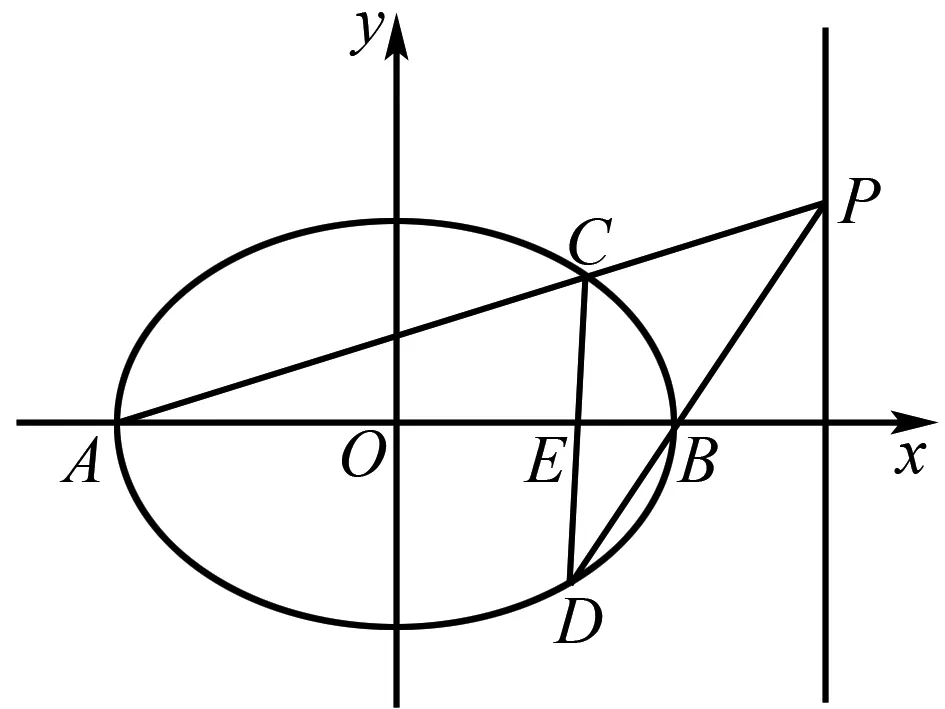
圖5

總結(1)如圖5所示，點P是直線x=6上的動點，可以說點P是主動點，由于它的運動才帶動了整個圖形的變化，因此設未知數可以從點P設起，設P(6,t).

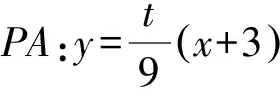
(4)借助對稱性，可以猜到CD所過的定點一定在x軸上.

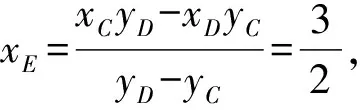
6 備考啟發

以上詳細分析的通性通法，可以遷移使用去解決2020年的山東卷和北京卷的圓錐曲線解答題，讀者可以自行嘗試.圓錐曲線題型多樣，結論眾多，而且高考經常創新問題情境，我們不可能讓學生見過一切結論，也不可能依靠題海戰術窮盡一切題型，唯一能做的就是不斷總結處理圓錐曲線的通性通法，不斷提升學生的運算求解素養，用有限的數學思想方法去應對無窮的題目，以不變應萬變.