函數零點問題中參數范圍的解法探究
賀鳳梅
(新疆伊犁鞏留縣高級中學 835400)
1 問題呈現
題目(新疆維吾爾自治區2022年普通高考第二次適應性檢測理科卷第10題)若函數f(x)=x3-ax2+ex-lnx有兩個零點,則a的取值范圍為( ).

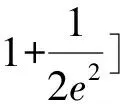
2 總體分析
本題題設簡潔,將函數、導數、零點等知識有機結合起來,多層次、多角度地考查了學生的數學思維和核心素養,同時考查了學生利用導數解決問題的能力,對邏輯推理、數學運算等提出了較高的要求.本題解法多樣,可以直接利用參變分離法求解;也可以利用分離函數法解答,利用導數的幾何意義,即切線的斜率求解入手,再從相切逆推至函數圖象相交的情況,進而求出參數的取值范圍;可以根據零點個數,分類討論細化解題,求出a的范圍;作為選擇題,還可以借助題設和選項的特點,利用排除法得出正確答案.但每種方法操作均不容易,在解題過程中會碰到一些障礙.下面具體分享一下,希望能幫助學生找到解決這類問題的突破口.
3 試題解答
視角1 分離參數,構造函數.
解法1 因為x>0,所以函數f(x)=x3-ax2+ex-lnx有兩個零點等價于f(x)=0有兩個正根.
分離參數,得
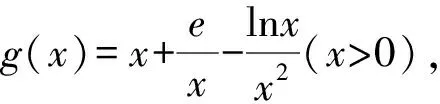
令h(x)=x3-ex+2lnx-1,則
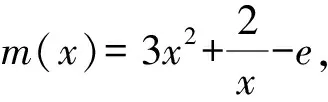

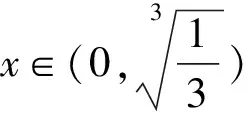
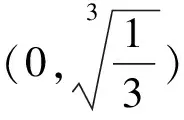


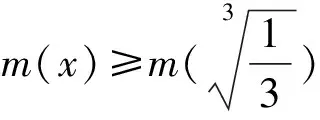
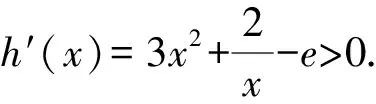
從而h(x)在(0,+∞)上單調遞增,

①

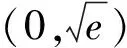
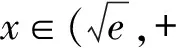
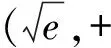

又當x→0時,
由洛必達法則知g(x)→+∞;
②
當x→+∞時,
則g(x)→+∞.
②
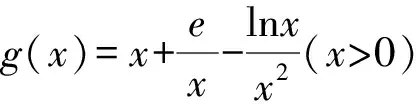
故選B.

下列關于函數f(x)=(2x-x2)ex的判斷正確的是( ).
(1)f(x)>0的解集是{x|0 (3)f(x)沒有最小值,也沒有最大值. 為了降低①的風險,我們有新的處理方式如下: 解法2 結合解法1, 下同解法1. 評注此種處理方法需要較高的觀察能力和配湊思維,值得我們思考和借鑒,提高解題能力.導數中有的零點是較難處理的,需要很多代數技巧作支撐,也要充分利用零點解題,尤其是隱零點,它可以幫助我們化超越函數為基本初等函數,還可能起到降次的作用,整體代換后還可能達到消元的目的. 視角2 分裂原函數,構造新函數. 解法3 令f(x)=x3-ax2+ex-lnx=0(x>0), “信息中心就‘選擇哪些考評維度,數據如何分類’等核心問題廣泛征詢各部門意見,形成建設思路;幾經例會討論確定管理平臺初步框架,多次深入各職能科室及臨床一線征詢意見,達成一致并上線運行。” 中心副主任趙前前回顧了平臺“由思到行”、逐步完善的建設歷程。試運行階段,平臺界面又經歷了4~5次較大改版,最終形成了各方普遍認同的,覆蓋全院、科室、醫生的三級績效評價體系。 令φ(x)=2x3-1+lnx, 所以φ(x)=2x3-1+lnx在(0,+∞)上單調遞增, 當x∈(0,x0)時,g′(x)<0, 當x∈(x0,+∞)時,g′(x)>0, 所以g(x)在(x0,+∞)上單調遞增. 整理,得切線斜率 整理,得t3+2lnt-et-1=0. ③ 代入直線y=ax-e中,得 故選B. 解法4 由x3-ax2+ex-lnx=0(x>0),得 同理可解. 評注解法4和解法3有異曲同工之妙,本質是兩個函數圖象整體平移,不再贅述,感興趣的同仁可以自行試驗一下.事實上,構造函數沒有特殊的要求,關鍵在于新函數易于研究,直觀形象就好.這一點對學生來說是一個挑戰,形異質同解法會帶來解題創新思路,對學生的能力提升大有裨益. 當然我們也可以直接轉化為函數f(x)=x3-ax2+ex-lnx的圖象與x軸交點的個數,分類討論求出參數a的范圍,此法求解原則上可行,但運算量較大.討論中要保證分類的科學性,做到既不重復,又不遺漏,是求解此問題的關鍵,限于篇幅,不再贅述. 視角3 特值驗證,小題速解. 解法5觀察選項與lnx無關,不妨設f(et)=0,則e3t-ae2t+et+1-t=0. 而a=0時,f(x)=x3+ex-lnx, 又ex>lnx,此時f(x)>0,無零點,不符合題意,排除選項D. 故選B. 評注作為選擇題,為了節約考試時間,我們期待小題能小做,速戰速決,所以結合題設及選項的結構特征,巧妙換元,特征值可排除錯誤選項,進而快速找到正確選項.這也需要學生有扎實的功底,在較短時間內發現非正確項的破綻. 題1(2016年全國Ⅱ卷第21題第(1)問)已知函數f(x)=(x-2)ex+a(x-1)2有2個零點.求a的取值范圍; 題2 (2017年全國Ⅱ卷第21題第(2)問)已知函數f(x)=ae2x+(a-2)ex-x.若函數f(x)有兩個零點,求a的取值范圍. 通過對此題多種解題方法的探究和比較,能很好地提升學生分析問題和解決問題的能力,逐步培養學生的核心素養,提升學習效率,讓學生所學的知識系統化.另外,分離變量、分離函數借助于數形結合是突破此類題的關鍵,尤其是曲線與直線相切地恰當使用.可以說,題目從知識立意、能力立意向價值引領、素養導向的轉變,很好地體現了試題的甄別功能.因此,我們的教學,絕不能夠僅僅停留在刷題的層面,一定要在能力和素養上下功夫.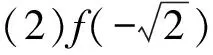

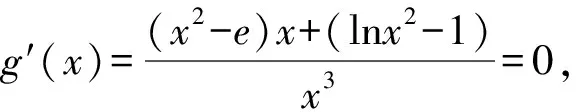
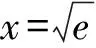
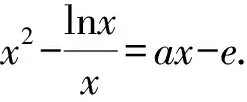
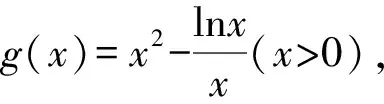
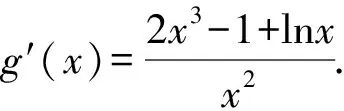
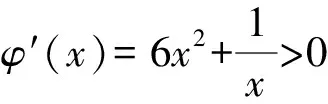
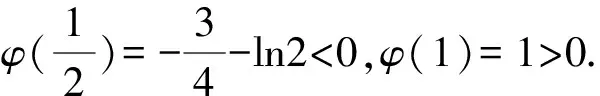
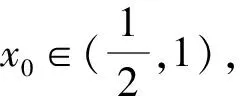
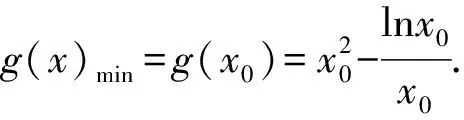
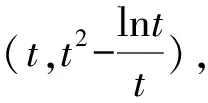
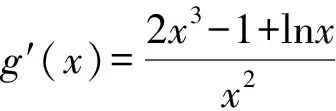
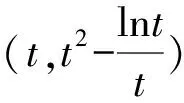

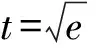
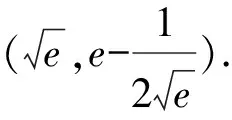
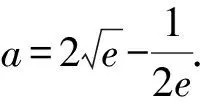
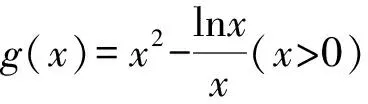
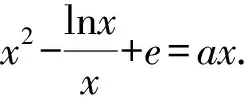
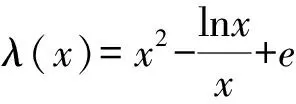
4 高考鏈接

