基于改進貝葉斯的重型數控機床可靠性研究

陳紅霞，張俊峰*，馬愛博，李宏悅，李晨光

(1. 內蒙古工業大學機械工程學院 呼和浩特 010051；2. 內蒙古自治區先進制造技術重點實驗室 呼和浩特 010051)

重型數控機床對現代軍工、航天、船舶、軌道交通、發電設備等重工業發展有重要意義[1]。目前，研究人員大多借鑒中小型數控機床的可靠性模型對重型數控機床進行可靠性分析[2]。重型數控機床具有加工工況復雜、故障溯源困難、維護成本較高、故障樣本數據匱乏等特點，這對重型數控機床的可靠性評估及后續研究都造成極大困難[3]。小樣本數據下的重型機床可靠性評估，是目前可靠性研究的一個難題[4]。

數控機床的可靠性研究最早開始于20 世紀70 年代[5]，前蘇聯專家對建立機床參數模型和機床工藝可靠性方面進行了相關研究[6]。近些年來，一些專家將貝葉斯理論引入小樣本條件下的重型數控機床可靠性建模[7]，根據先驗信息和主觀經驗進行模型參數估計[8]。文獻[9]采用威布爾雙參數和三參數分布對重型數控機床零部件或系統建模[9]。文獻[10]采用極大似然估計法和Edgeworth 級數法對重型數控機床的故障模型進行參數估計，并解釋參數估計結果與數據擬合的關系。文獻[11]利用第二類極大似然方法得到折合因子的貝葉斯估計[11]。文獻[12]在馬爾科夫鏈蒙特卡洛方法(Markov Chain Monte Carlo, MCMC)方法的基礎上針對數據的多源性，建立多源異種數據融合模型，為小樣本的可靠性建模提供新思路。上述研究對小樣本數據下的可靠性建模問題提出了不同的方法，給重型數控機床可靠性建模及評估奠定了理論基礎。

本文基于改進的貝葉斯方法對重型數控機床進行可靠性建模與評估。首先，選取雙參數的威布爾分布對機床故障數據進行擬合，采用極大似然參數估計法和貝葉斯參數估計法對可靠性模型求解。其次，對傳統的貝葉斯估計法進行改進，得到分層貝葉斯模型，通過對比分析及仿真實驗，證明改進后的貝葉斯模型在小樣本數據條件下更具有優越性。最后，利用分層貝葉斯模型對該機床進行可靠性評估，得到其理論故障間隔時間。

1 數控機床的可靠性模型參數估計

1.1 傳統可靠性模型

一般地，對系統建立可靠性模型均采用雙參數威布爾分布。以重型數控機床故障間隔時間為參數，經過變換得到服從威布爾分布的可靠性模型。此時，機床可靠性服從威布爾分布的概率密度函數和概率分布函數分別為：

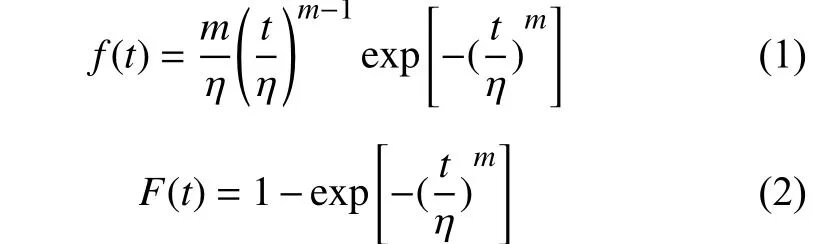
式中，m和η 分別為威布爾分布的形狀參數和尺度參數；t為機床的故障時間。

1.2 極大似然估計法

一般地，采用極大似然估計對分布函數進行參數估計。當已知分布模型中有未知參數θ1,θ2,···,θk時，可以建立似然函數表達式：

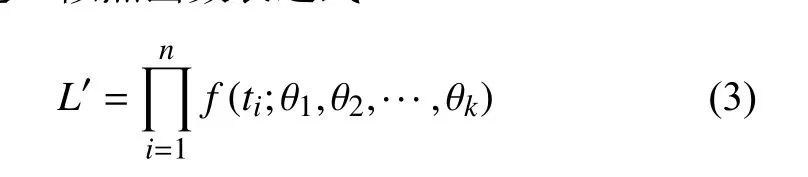
式中，ti為實際采集的數據子樣(i=1, 2, ···,n)。

在威布爾分布模型中，未知參數為m和η，將式(1)的威布爾分布概率密度函數代入式(3)中，建立的極大似然函數為：

1.3 基于貝葉斯理論的參數估計

由貝葉斯參數估計理論可知，在對分布函數的參數估計中，所有未知參數都被認為是隨機變量。求解待估參數值時，需要先根據觀測數據和主觀經驗設定其模型的先驗分布，進而求出參數估計結果。其中，先驗分布的選擇優劣會直接影響模型參數估計的精度。

基于貝葉斯理論對重型數控機床建立可靠性模型，具體思路為在研究對象樣本數據和先驗信息的基礎上，建立其貝葉斯模型，計算模型參數的后驗分布并得出相應的概率分布。

結合貝葉斯定理分析可知，分布模型參數的后驗分布可以表示為：

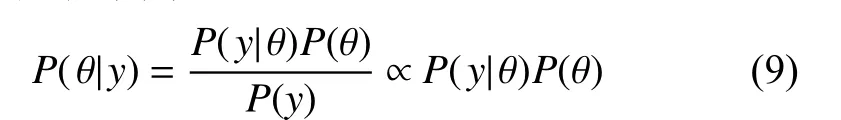
式中，θ 為待估計的參數；y為基于觀測數據的信息；P(θ)為 參 數 θ 的先驗 概 率；P(y|θ)是設定 參 數θ 條件下的數據所服從的后驗分布；P(y|θ)/P(y)為事件y對參數設定的支持程度，即似然函數。

因為正態分布是威布爾分布的共軛先驗分布模型，所以設定威布爾分布的參數m和η 服從正態分布，這里用N來表示。

經過推導，得到重型機床基于貝葉斯理論的可靠性模型，如式(10)所示：

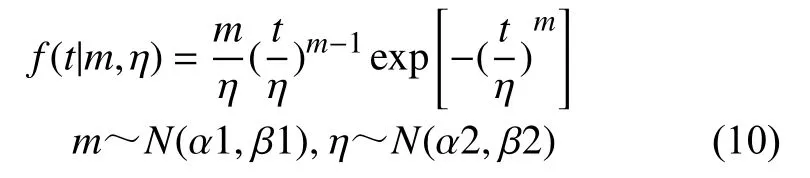
1.4 層次貝葉斯模型

為了優化貝葉斯參數估計的方法，將待估參數的先驗分布進一步分化，得到層次貝葉斯模型。層次貝葉斯模型理論上可以分為N層，但隨著分化層數的增加，模型的計算效率逐漸降低。為了保證計算效率，采用兩層貝葉斯模型進行分析。

由一般貝葉斯模型可知，m～N(α1,β1)為參數m的先驗分布， η～N(α2,β2) 為 參數 η的先驗分布。將α2～unif(α1′,β1′),β2～unif(α2′,β2′)分別作為參數m, η 的先驗分布，這樣就得到了更進一層的貝葉斯模型，這里稱 α2,β2為超參數，unif 表示均勻分布，表達如下：

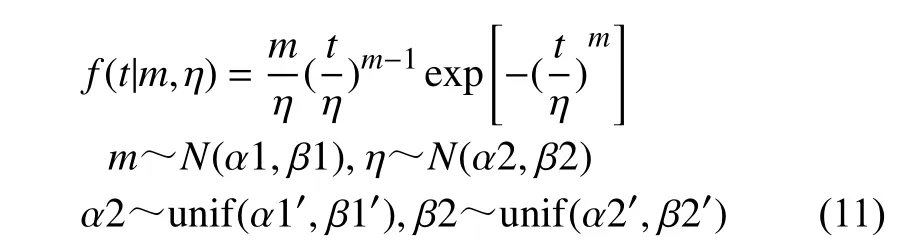
經過上式推導，即可得到基于層次貝葉斯理論的可靠性模型。

1.5 貝葉斯模型的求解方法

求解貝葉斯模型的參數需要計算高維積分的邊緣后驗分布，而且隨著模型組成的復雜會使參數求解變得更加困難。通過引入 MCMC 方法對模型進行數據模擬、迭代以提升參數求解的效率。該方法中包含多種抽樣方法，包括Metropolis-Hastings 抽樣方法和 Gibbs 抽樣方法。其中，Metropolis-Hastings抽樣方法更為高效，具體操作流程如圖1 所示。

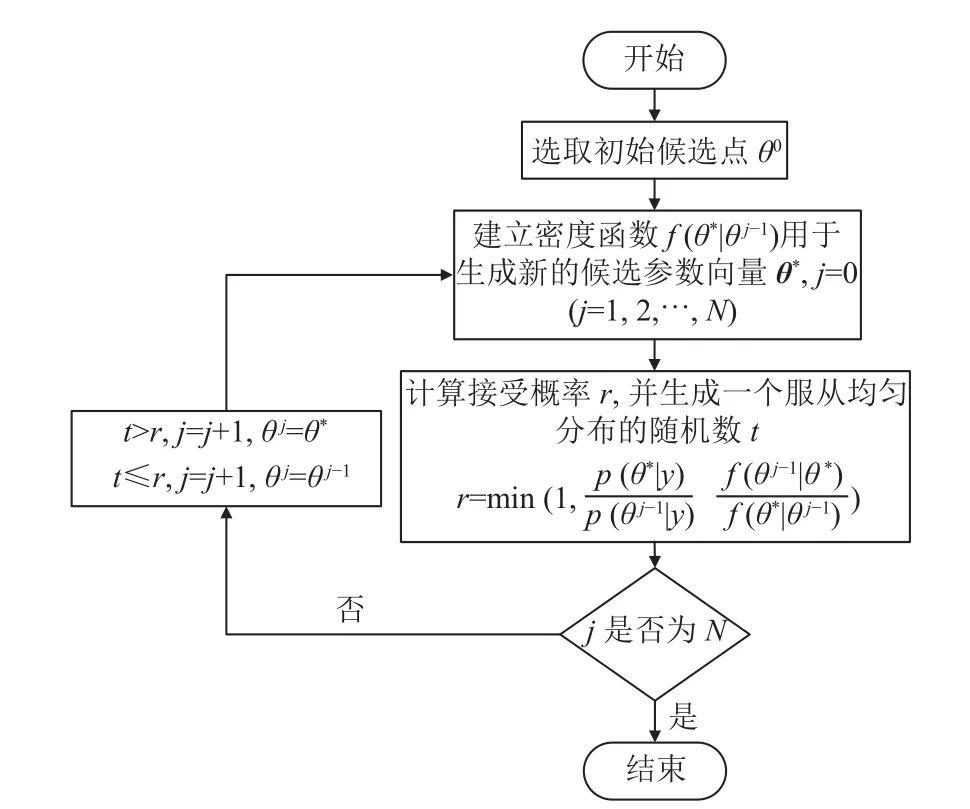
圖1 蒙特卡洛仿真流程

通過MCMC 法處理得到模型待估參數的后驗分布，取其期望值作為參數估計的結果，基于排序取分位數法，可以求出待估參數的置信區間。

1.6 參數估計結果分析

為了分析參數估計結果的優劣，本文采用統計學中的均方根誤差值(normalized root mean square error, NRMSE)，NRMSE 值越小則結果精度更優。計算方法為：

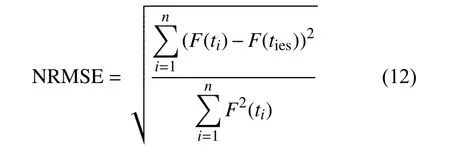
式中：F(ti)是機床的累計故障概率，F(ties)是將參數估計值代入累積故障概率函數后所得到的累積故障概率值。

2 建立重型數控機床的可靠性模型

重型機床故障數據樣本量較小、數據跨度較大、故障發生具有不確定性，若采用一般統計學方法無法對此類問題進行有效分析，本文基于貝葉斯理論進行分析，可以一定程度優化分析結果。

2.1 故障數據預處理

本文采集某企業近3 年內，某型號重型數控機床的停機維修記錄共58 條。通過數據預處理，得到該機床的故障間隔時間，其中部分結果為22 h，23 h，24 h，···，912 h，936 h，1 248 h。

2.2 參數估計結果

將故障間隔時間代入機床的雙參數威布爾分布可靠性模型中，利用最大似然參數估計法和貝葉斯參數估計法分別對分布模型的參數進行求解。采用最大似然參數估計法得到的結果如表1 所示，用下標MLE 來表示。

表1 最大似然參數估計結果

將機床的故障間隔時間從大到小排列，代入式(13)所示的中位秩公式：

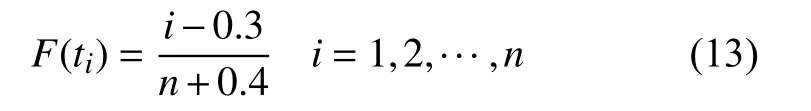
計算該重型機床實際的累計失效概率密度，得到其點位分布圖，如圖2 所示。

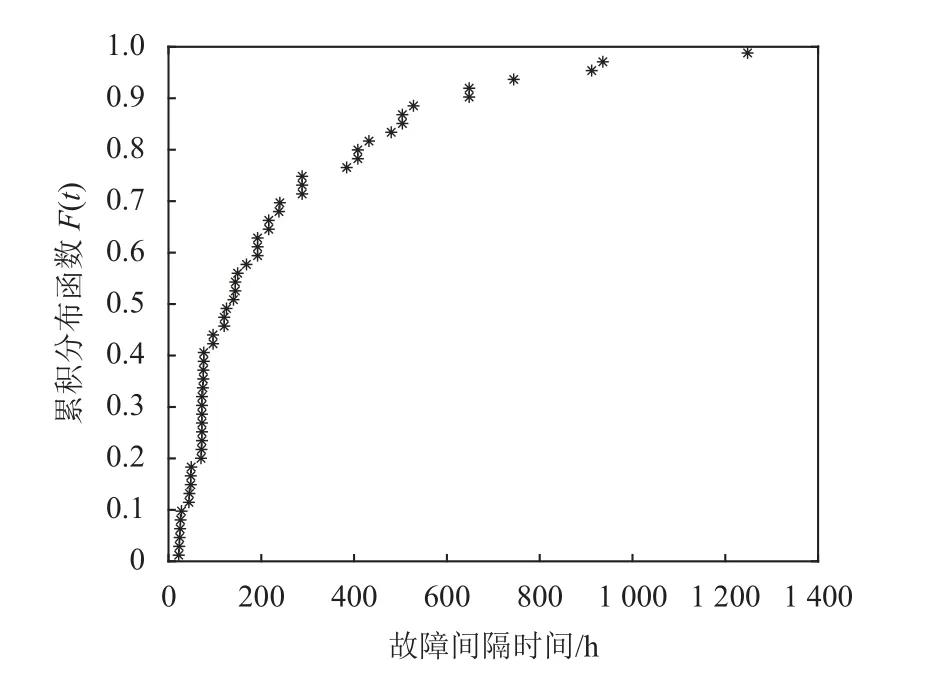
圖2 樣本的數據點分布圖

將參數估計結果代入機床的可靠性模型，得到基于威布爾分布的機床擬合累計失效概率曲線，如圖3 所示，圖中虛線為95%置信區間的上下限。通過比較兩條曲線的重合度來分析模型的擬合精度。

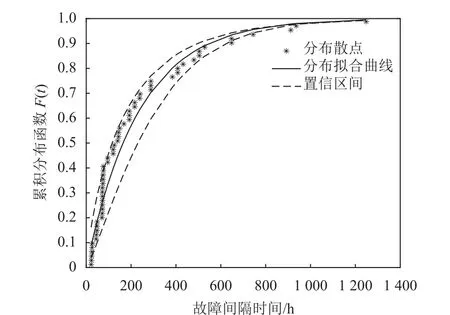
圖3 最大似然估計下的威布爾模型分布函數

由圖3 可知，通過極大似然估計得到的機床可靠性模型分布曲線，部分與參考數據點位重合，沒有重合的部分也基本分布在置信區間內。

基于貝葉斯理論得到的參數估計結果如表2 所示，其中，用下標GBR 表示一般貝葉斯參數估計的結果，用下標HBR 表示分層貝葉斯參數估計的結果。

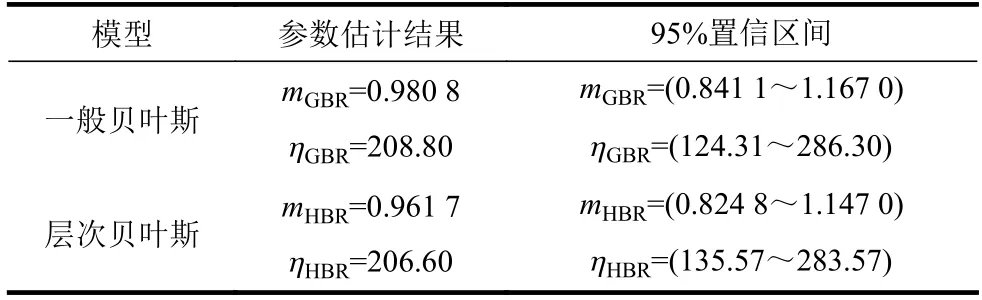
表2 一般貝葉斯和層次貝葉斯參數估計結果

通過對參數進行多層迭代，輸入不同的初始值，構造馬爾科夫鏈然后觀察其抽樣迭代過程是否收斂，運算迭代過程如圖4、圖5 所示。將α1=1,α2=200,β1=β2=0.5代 入 式(10)，α1=1,β1=0.5,α1′=α2′=0,β1′=100,β2′=1代入式(11)，得到待估參數的后驗分布，如圖6、圖7 所示。

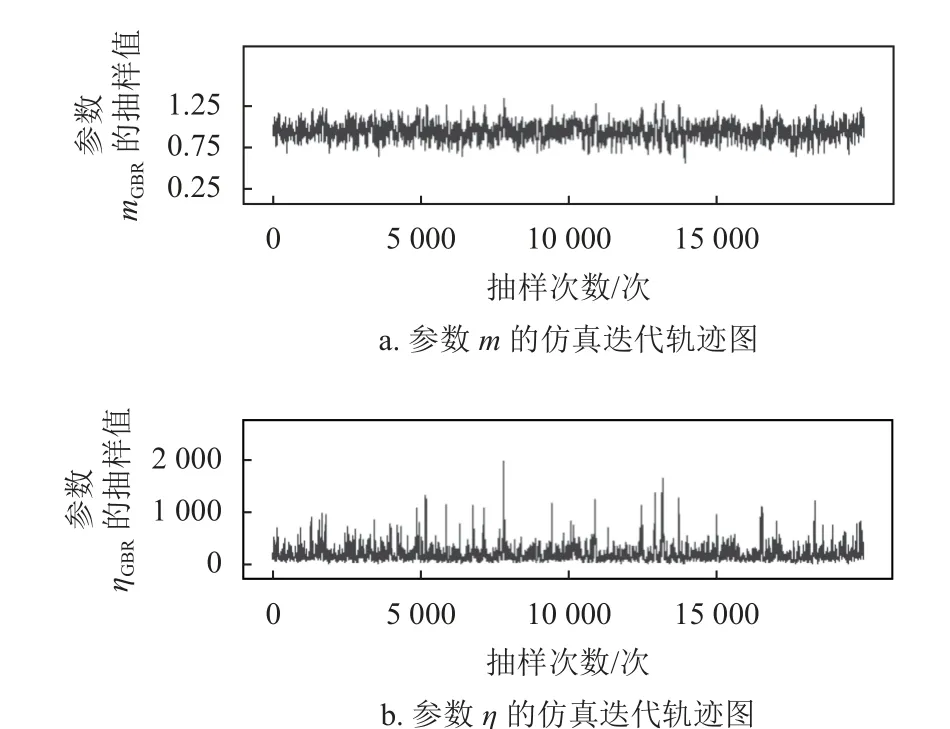
圖4 基于一般貝葉斯模型的仿真迭代軌跡圖

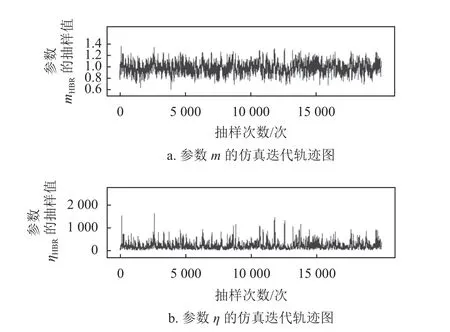
圖5 基于分層貝葉斯模型的仿真迭代軌跡圖

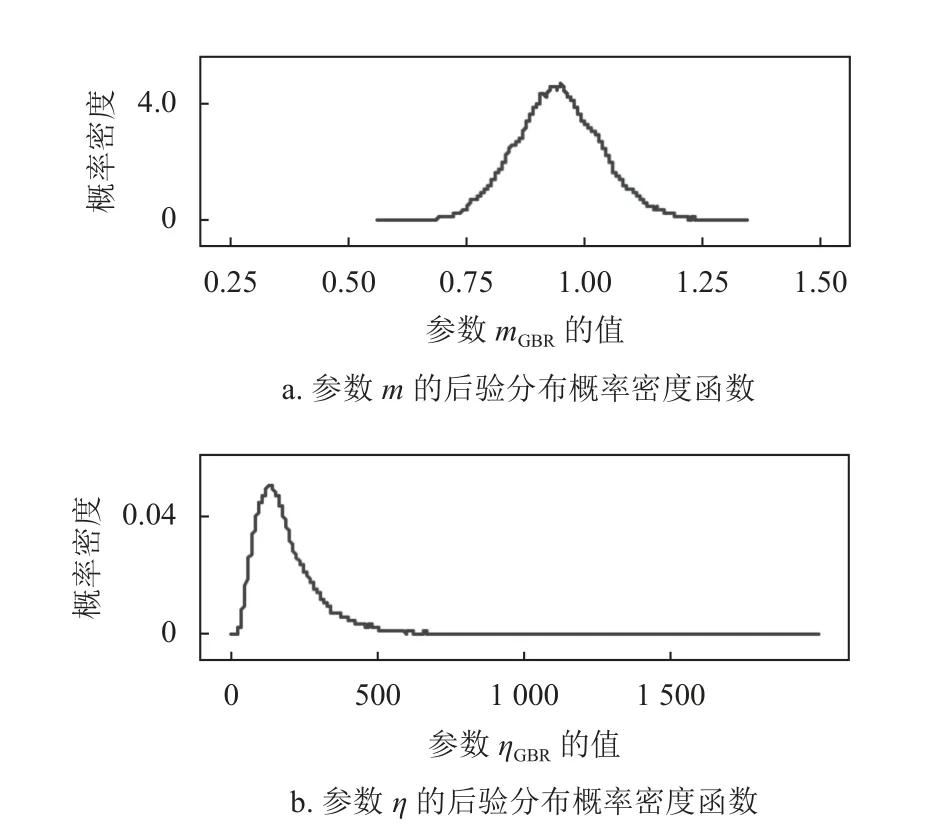
圖6 基于一般貝葉斯模型的參數后驗分布概率密度函數

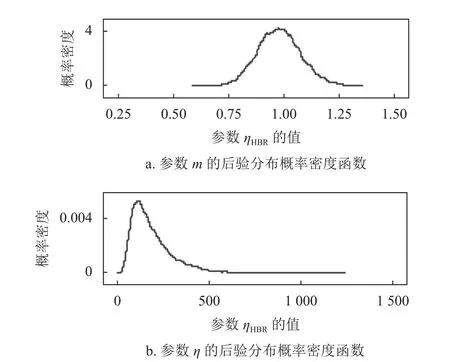
圖7 基于分層貝葉斯模型的參數后驗分布概率密度函數

從待估參數的后驗分布圖中可以看出，分層貝葉斯參數估計的結果更加集中。將參數估計結果分別代入式(1)、式(13)中，得到圖8、圖9 所示的分布曲線。由此可知，貝葉斯模型與傳統的模型相比，其擬合曲線與真實數據的重合度更高。

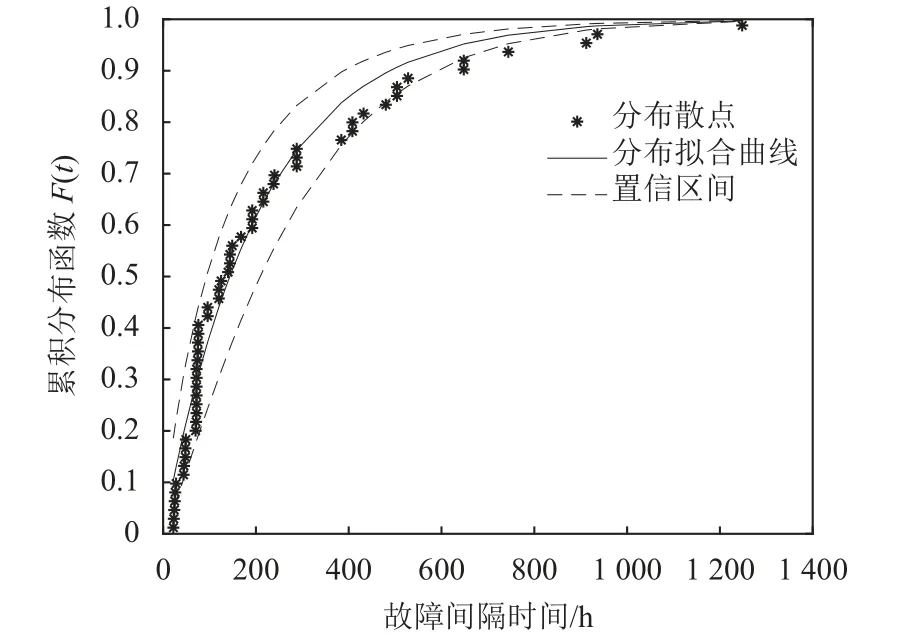
圖8 一般貝葉斯估計下的曲線分布

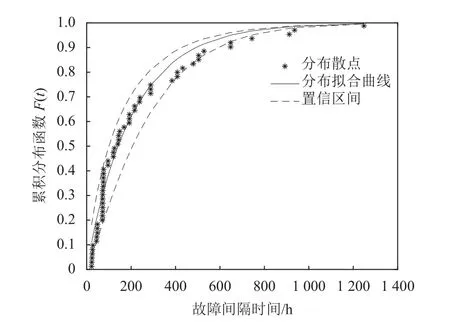
圖9 分層貝葉斯估計下的曲線分布

2.3 結果分析

將機床的3 種可靠性模型代入式(12)，計算得到NRMSE 值，結果分別為MLE=0.097 1，GBR=0.121 0，HBR=0.090 0。對比結果可知：分層貝葉斯模型相對于其他兩個模型來說誤差值更小，數據擬合效果更優；基于極大似然估計法模型的NRMSE值低于一般貝葉斯模型的NRMSE 值。雖然此處傳統可靠性模型精度比一般貝葉斯模型更優，可是隨著經驗信息的豐富，優化參數先驗信息的設定后，可以逐漸改善參數估計的精確性。

2.4 不同樣本量下的3 種參數估計方法對比

改變數據樣本的容量，分別使用上述3 種參數估計方法，經過計算求出不同樣本容量下的標準均方根誤差值，結果如圖10 所示。

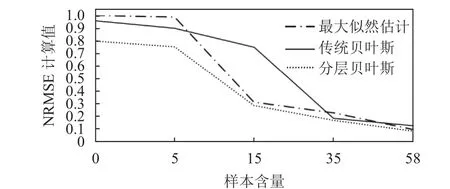
圖10 不同樣本量下的建模NRMSE 值

從圖中可以看出，隨著樣本容量的增加，經過3 種參數估計方法得到的可靠性模型NRMSE 值均在下降，說明建模誤差在降低，精度越來越好，當數據量趨于大數據樣本時，貝葉斯方法依然有良好的可靠性。但當數據量較小時，其NRMSE 值更小，分層貝葉斯參數估計法有顯著優勢。特別是在樣本量趨于0 時，基于極大似然估計建模得到的NRMSE 值近似于1，而基于貝葉斯理論建模得到NRMSE 值依然小于1，說明在樣本量很小時，傳統的方法幾乎失去精確性，而基于貝葉斯理論得到的結果依然有效。綜上所述，在數據量不足時，分層貝葉斯模型的擬合效果更優。

2.5 仿真驗證

基于matlab 軟件，將服從形狀參數Beta=2 及尺度參數Eta=1 的雙參數威布爾分布函數隨機篩選10 組數據，把產生的小樣本量代入到3 種參數估計方法中，得到表3 的結果。

表3 仿真估計結果對比

經過仿真分析也可以驗證分層貝葉斯在進行小樣本參數估計方面的優勢，其估計的參數相對來說最接近真實值。

3 可靠性評估

平均故障間隔時間(mean time between failures,MTBF)是常用的可靠性評價指標之一，是指產品從發生故障到下一次發生故障的平均工作時間，其表達式為：

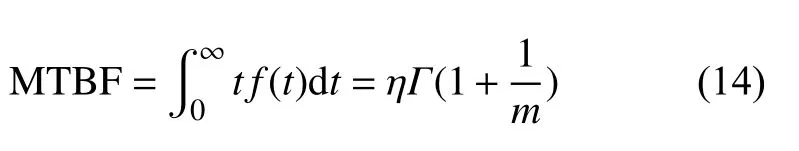
式中，f(t)為概率密度函數。

將層次貝葉斯參數估計結果代入式(14)后，求得機床平均故障間隔時間為M TBF=210.215 h。分析可知，計算得到的MTBF 值小于所采集數據中的最大值1 248.000 h，210.215 h 大于所采集數據中的60%，經過排序分析處于中上位置。由此可見，平均故障間隔時間對于機床預防故障和維修保養有參考意義，說明了貝葉斯理論對于重型機床可靠性建模的有效性。

4 結 束 語

本文在重型數控機床故障數據小樣本條件下，基于貝葉斯理論建立服從威布爾分布的可靠性模型，并對傳統貝葉斯模型進行改進，得到分層貝葉斯模型。引入MCMC 算法求解貝葉斯模型的參數估計結果，對比極大似然估計法與貝葉斯參數估計的優劣，結果顯示這兩種參數估計結果近似，但貝葉斯參數估計法得到的參數置信區間更窄。采用NRMSE 分析參數估計結果精度，隨著樣本數據容量增大，傳統參數估計法與貝葉斯參數估計法趨于一致，當數據樣本較小時，分層貝葉斯模型得到的建模精度更高。對貝葉斯理論模型進行仿真實驗，結果表明貝葉斯參數估計是有效的。利用貝葉斯可靠性模型對該重型數控機床進行可靠性評估，在機床故障數據小樣本條件下，其評估結果更精確有效，對重型數控機床的可靠性研究有重要意義。