基于Optistruct某公交車后圍板多目標形貌優化設計
徐明欣,馬彩峰,韋淇鵬,陳 劍,蘇秀花
(1.柳州五菱汽車工業有限公司,廣西 柳州 545007;2.東風柳州汽車有限公司,廣西 柳州 545005)
0 引言
在某開發平臺上,需要將后對開門更改為公交車封閉行李艙,同時滿足降本需求,盡量減少原內板支撐結構,用沖壓板材通過合理布置加強筋形式,提高公交車后圍板剛度,保證結構頻率。
憑借工程師的經驗構建多種加強筋方案,然后逐一進行有限元方法驗算剛度和模態,得到的只是可行性設計而不是最優設計,這就需要采用先進的優化理念與分析工具尋求最優化的設計。形貌優化是在板金結構中尋找最優加強筋分布的概念設計方法,用來設計薄壁結構的強化壓痕,在不增加結構重量的前提下,增加結構的剛度、模態頻率等。形貌優化通過定義一個或若干個起筋區域,設定加強筋的最小寬度、起筋角度和高度即可進行計算。同時還可以考慮可加工性,軟件提供多種加強筋的布置形式。優化后的加強筋形狀可以通過OSSmooth工具直接產生有限元或CAD數據,供設計人員參考[1]。
1 多目標優化函數
通過初步試算,發現公交車鈑金后圍板在兩個位置點剛度較低,優化分析中需要提高兩個工況剛度,同時不能降低后圍板模態頻率,此問題屬于多目標優化。在Optistruct中,多目標優化有多種處理方法,比較簡單的方法是試算原方案分析結果,將多個優化目標中的一個作為目標函數,其余的目標作為約束響應,比如:柔度不大于原設計的柔度;重量不大于原設計的重量;變形不大于原設計的變形;一階頻率不低于原設計的頻率等等。對于某些希望改進的參數,還可以把約束設計更嚴格,比如重量不大于原來的80%,但這需要經驗和反復的嘗試[2]。
對于本研究的問題,可以把兩個工況剛度綜合為一個目標,1階模態頻率作為約束考慮,或者將兩個工況剛度和模態頻率綜合在多目標方程中。前者把兩個工況綜合為一個目標可以采用線性加權法和最小柔度法來處理。優化是不斷嘗試的結果,本研究采用3種方法對后圍板進行形貌優化分析。
1.1 線性加權和法優化函數
柔度反映的是結構的應變能,是結構剛度的倒數。加權柔度是經典拓撲優化中考慮多工況的一種方法,它是每個獨立工況的柔度加權總和,是針對整個結構的全局響應[3]。采用線性加權和法將兩個工況剛度轉化為單目標問題,同時約束1階模態頻率進行優化求解。
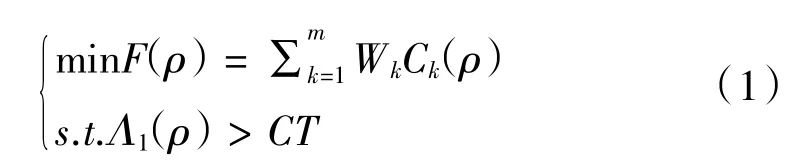
其中,W噪為第K個工況結構柔度加權,一般情況下W噪=1;C噪(ρ)為第K個工況結構柔度,是響應變量;Λ1(ρ)為結構一階固有頻率,是響應變量;CT為常數值。
1.2 最小柔度法優化函數
對于非凸優化問題,線性加權和法不能保證所有工況均得到最優解,現今研究剛度最大問題,可以采用折衷法等效為柔度最小問題來研究。折衷法多目標拓撲優化,即將單獨工況載荷集中在一個工況中,用統一工況描述結構綜合柔度,同時約束一階模態頻率進行優化求解。

其中,C(ρ)為結構綜合柔度,是響應變量;Λ1(ρ)為結構一階固有頻率,是響應變量;CT為常數值。
1.3 多目標方程法優化函數
結構多目標優化同時考慮靜態多剛度目標和動態振動頻率目標的優化,可以使用多目標優化的綜合目標函數[4]。

(3)中,C1(ρ)為噪=1時結構的柔度,是響應變量;為噪=1時原始模型的柔度(原始模型的柔度最大);為噪=1時單獨做柔度優化計算后的柔度(因為經過優化得到最小柔度值);Λ(ρ)為結構一階固有頻率,是響應變量;Λmax為單獨做頻率優化計算后的一階固有頻率(經過優化得到最大頻率值);Λmin為原始模型的一階固有頻率(原始模型的頻率最小);w為加權值,設置在0~1之間,一般情況下w=0.5。
2 后圍板多目標優化
形貌優化主要用于提高鈑金部件的剛度,多數情況下設置的響應類型為節點位移和模態頻率值,這兩者既可以做約束,也可以做目標函數。在Optistruct軟件設置中,要注意加強筋最小寬度推薦值為單元平均尺寸的1.5~2.5倍,起筋角推薦值為60°~75°。形貌優化前,確保設計區域的單元方向一致,勾選緩沖區設置,系統將遠離非設計區域放置形狀變量,如果不勾選,則筋和非設計空間的邊界會產生一個突變。加強筋模式組合中常用的有線性、平面對稱等選項。通過上、下邊界限制值來邊確定起筋方式為凸筋或凹筋,邊界忽略表示不保留設計區域內的載荷與約束。
圖1為某公交車后圍板優化模型,圖中淺灰色區域為設計空間。要求加強筋水平放置,且加強筋的最小寬度25 mm、起筋角60°、起筋深度最大15 mm,設置緩沖區,根據優化結果確定凸筋或凹筋,不保留設計區域內的載荷與約束。確定設計變量后,固定約束后圍板四周,綜合考慮P1點變形、P2點變形和一階模態頻率。
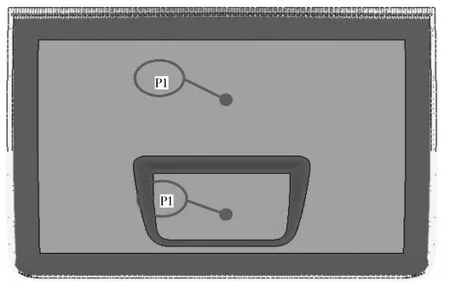
圖1 某公交車后圍板優化模型
2.1 線性加權和法優化模型
分別在P1、P2兩個位置點加載1000 N載荷,并將兩種載荷定義在兩個工況中。P1、P2點變形通過weighted comp的響應類型,將兩個工況線性加權和為一個響應,并設置該響應為最小目標函數,同時約束一階模態頻率大于32 Hz,經過10次迭代計算,得出優化結果。圖2是線性加權和優化加強筋分布云圖,優化后結構柔度8500 mm/kN,一階模態頻率32.3 Hz。
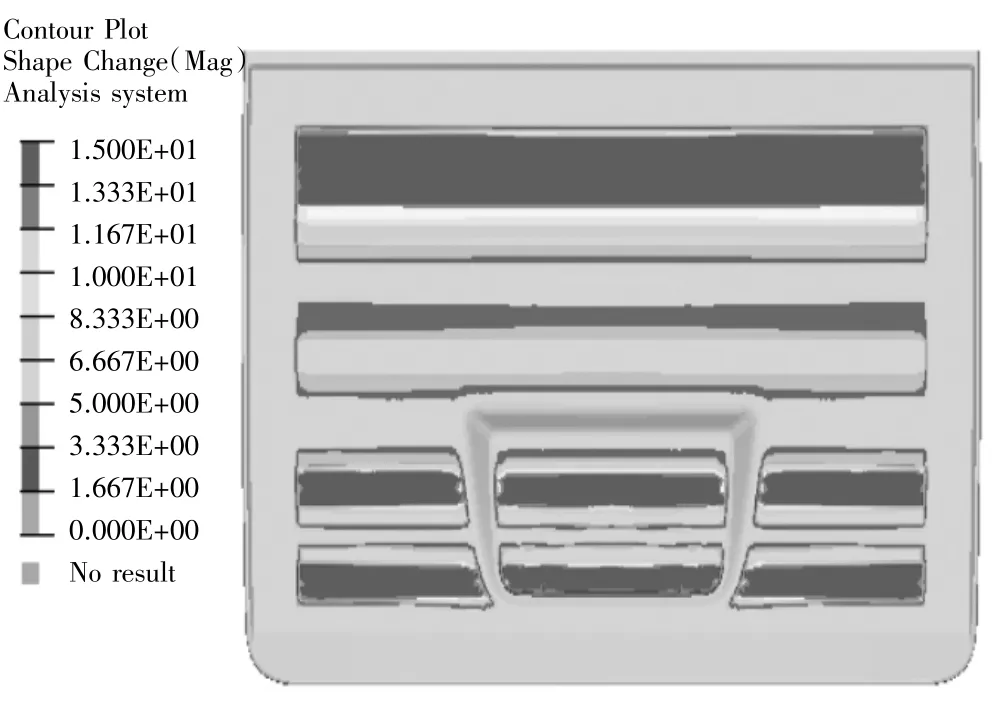
圖2 線性加權和優化加強筋分布云圖
2.2 最小柔度法優化模型
分別在P1、P2兩個位置點加載1000 N載荷,并將兩種載荷定義在一個工況中。P1、P2點變形定義為compliance的響應類型,并設置該響應為最小目標函數,同時約束一階模態頻率大于32 Hz,經過11次迭代計算,得出優化結果。圖3是最小柔度優化加強筋分布云圖,優化后結構柔度8300 mm/kN,一階模態頻率35.0 Hz。
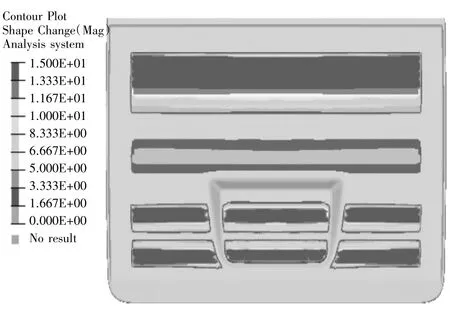
圖3 最小柔度優化加強筋分布云圖
2.3 多目標方程法優化模型
利用Optistruct中提供的自定義函數考慮結構柔度和模態頻率,首先計算出原始模型的柔度為50100 mm/kN、原始模型1階頻率為30.3 Hz、單獨最小柔度優化后模型柔度8236 mm/kN、單獨最大頻率優化后模型1階頻率39.3 Hz。然后按照公式(4)在dequation中編輯軟件可識別的自定義函數,接下來定義為function的響應類型,將方程中的變量(柔度和頻率)和多目標優化函數關聯起來,設置該響應為最小目標函數,經過30次迭代計算,得出優化結果。多目標方程優化加強筋分布云(圖4),優化后結構柔度8700 mm/kN,一階模態頻率37.6 Hz。

圖4 多目標方程優化加強筋分布云圖
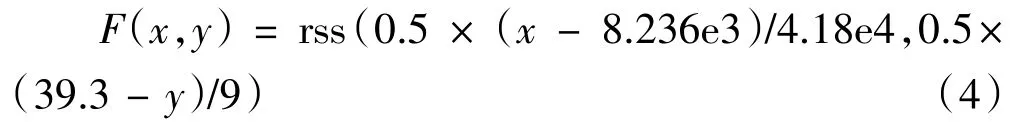
是各種優化方法數據對比見表1。從表中可以看出,最小柔度法優化方法的結構柔度和一階模態頻率均優于線性加權和法優化方案,該方法避免了線性加權和法不保證所有工況均得到最優解的情況,在多目標剛度優化中更具優勢。多目標方程優化法可通過加權值來平衡柔度和一階頻率,權重0.5時后圍板多目標方程優化方法比最小柔度約束優化方法得出的結構柔度增大5%,一階頻率提高7%。
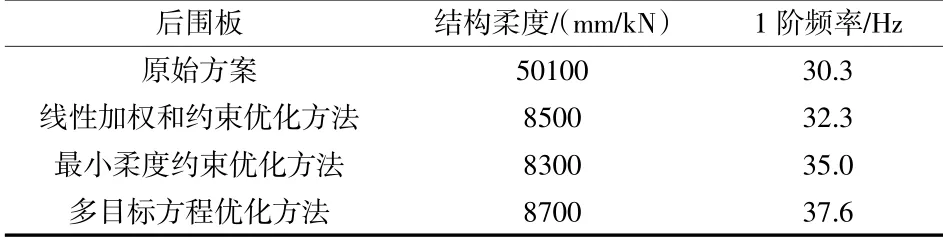
表1 各種優化方法數據對比
3 后圍板優化模型
選用多目標方程優化方法的后圍板方案,優化后的加強筋形狀通過OSSmooth工具直接產生CAD數據,設計人員在此基礎上考慮外觀件的美化因素,生成最終數模。是后圍板優化模型見圖5;原內板支撐結構見圖6。原結構重18 kg,優化鈑金結構后圍板重10 kg,重量降低44%,且原結構存在大量焊接和粘膠工藝,優化結構直接沖壓成型即可。

圖5 后圍板優化模型

圖6 原內板支撐結構
在兩種方案后圍板的相同位置,各選取6個評估點,對不同評估點進行靜剛度計算,得出表2各評估點剛度數值,可以看出優化結構較原內板支撐結構剛度分布更均勻,且平均剛度提高22%。
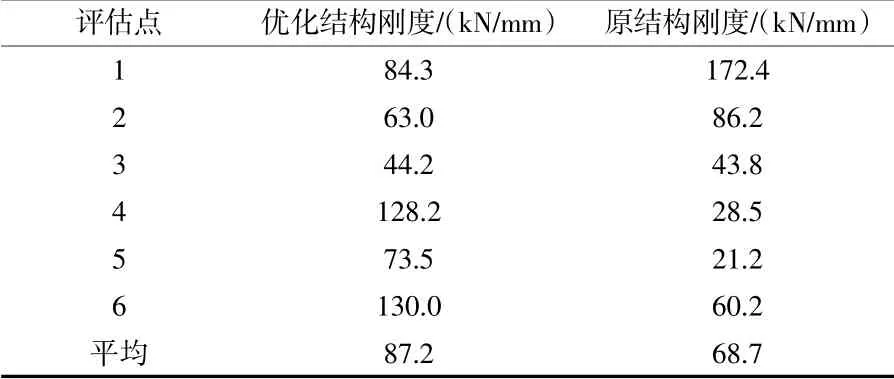
表2 各評估點剛度數值
4 結論
通過三種優化方法的分析結果對比,最小柔度法避免了線性加權和法不保證所有工況均得到最優解的情況,在多目標剛度優化中更具優勢。而多目標方程優化法可適用于復雜不同約束的多剛度情況,如車身彎曲工況和扭轉工況,同時通過加權值來平衡多個目標響應關系,在多目標優化中應用更廣泛。本文優化后設計方案與原方案相比較,柔度下降了83%,一階固有頻率提高了24%,這說明優化在兩組變量之間很好地找到了平衡點,較大地提高了部件本身的結構力學和NVH性能。優化后圍板結構重量降低44%,評估點平均剛度提高22%,且無焊接和粘膠工藝,較大降低成本,提高結構性能。

